SAT Test Prep

CHAPTER 6
WHAT THE SAT MATH IS REALLY TESTING

Lesson 6: Finding Alternatives

Keep Your Options Open

There are often many good ways to solve an SAT math problem. Consider different strategies. This gives you a way to check your work. If two different methods give you the same answer, you”re probably right!

Numerical Analysis—Plugging In

Let”s come back to the problem we saw in Lesson 4:

If and , then what is the value of

Back in Lesson 4 we solved this using substitution, an algebraic method. Now we”ll use a numerical method. Notice that the equation contains two unknowns. This means that we can probably find solutions by guessing and checking. Notice that the equation works if and . But—darn it—the problem says ! No worries—notice that and also work. (Check and see.) Now all we have to do is plug those numbers in for x and 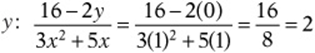. same answer, whole different approach.

“Plugging in” works in two common situations: when you have more unknowns than equations and when the answer choices contain unknowns. Always check that your numbers satisfy the conditions of the problem. Then solve the problem numerically, and write down the answer. If the answer choices contain unknowns, plug the values into every choice and eliminate those that don”t give the right answer. If more than one choice gives the right answer, plug in again with different numbers.

If , then what is the value of m in terms of n?

Because the choices contain unknowns, you can plug in. Pick a simple number for m to start, such as 1. Plugging into the equation gives , which has the solution . Now notice that the question asks for m, which is 1. Write that down and circle it. Now substitute 2 for n in the choices and see what you get:

(A) 3

(B) 0

(C) 1

(D) 1/5

(E) 2/5

Only (C) gives the right answer.

Algebraic Analysis

You can also solve the problem above algebraically:

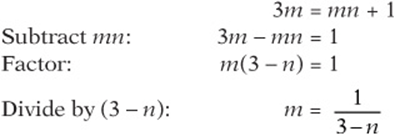
Testing the Choices

Some SAT math questions can be solved just by “testing” the choices. Since numerical choices are usually given in order, start by testing choice (C). If (C) is too big, then (D) and (E) are too big, also, leaving you with just (A) and (B). This means that you have only one more test to do, at most, until you find the answer.

If , what is the value of n?

(A) 2

(B) 3

(C) 4

(D) 5

(E) 6

Here you can take an algebraic or a numerical approach. That is, you can solve the equation for n or you can “test” the choices to see if they work. For this lesson, we”ll try the “testing” strategy. Since the choices are given in ascending order, we”ll start with the middle number, (4). Substituting 4 for n gives us on the left side, which equals 48, not 24. (It”s okay to use your calculator!) Since that doesn”t work, we can eliminate choice (C). But since it”s clearly too big, we can also rule out choices (D) and (E). That”s why we start with (C)—even if it doesn”t work, we still narrow down our choices as much as possible. Now just test either (A) or (B). Notice that (B) gives us , which equals 24, the right answer.

Now try solving the problem algebraically, and see if it”s any easier!

Concept Review 6: Finding Alternatives

1. When can a multiple-choice problem be solved by just “testing the choices”?

2. When solving by testing the choices, why is it often best to start with choice (C)?

3. When testing the choices, when is it not necessarily best to start with choice (C)?

4. When can you simplify a multiple-choice question by plugging in values?

5. What are the four steps to solving by plugging in values?

6. Why is it best to understand more than one way to solve a problem?

SAT Practice 6: Finding Alternatives

Try to find at least two different ways of solving each of the following problems, and check that both methods give you the same answer.

1. If and , which of the following expresses x in terms of m and n?

2. Three squares have sides with lengths a, b, and c. If b is 20% greater than a and c is 25% greater than b, then by what percent is the area of the largest square greater than the area of the smallest square?

(A) 20%

(B) 50%

(C) 75%

(D) 125%

(E) 225%

3. Jim and Ellen together weigh 290 pounds. Ellen and Ria together weigh 230 pounds. All three together weigh 400 pounds. What is Ellen”s weight?

(A) 110 lbs

(B) 120 lbs

(C) 130 lbs

(D) 140 lbs

(E) 170 lbs

4. A painter used one-fourth of her paint on one room and one-third of her paint on a second room. If she had 10 gallons of paint left after painting the second room, how many gallons did she have when she began?

(A) 19

(B) 24

(C) 28

(D) 30

(E) 50

5. If and , what is the value of s in terms of t?

(A) 35t

(D) 31t

(E) 70t

Answer Key 6: Finding Alternatives

Concept Review 6

1. There are many situations in which this is possible, but perhaps the most common is where you”re asked to find the solution of an equation, and the choices are ordinary numbers.

2. Because the answer choices are usually presented in numerical order. If choice (C) doesn”t work, you may be able to tell whether it is too big or too small, and thereby eliminate two other answers as well. This way, you will only need to “test” one more choice to get the answer.

3. When it is not easy to tell whether the choice is “too big or too small,” or when there is no pattern to the choices.

4. Usually, when the answer choices contain unknowns or represent ratios of unknowns; also when the problem contains more unknowns than equations.

5. (1) Check that the values satisfy any given equations or other restrictions, (2) write down the values you are plugging in for each unknown, (3) solve the problem numerically and write down this number, and (4) plug in the values to every choice and eliminate those that don”t give the right answer. If more than one choice gives the right answer, plug in different numbers.

6. Because the two methods can provide a “check” against one another: if they both give the same answer, you are almost certainly right!

SAT Practice 6

1. Method 1: The problem asks you to solve for x in terms of m and n. Notice that every choice contains the expression m – n.

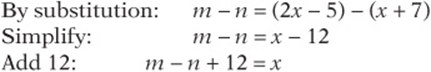
So the answer is (D).

Method 2: Just plug in simple values for the unknowns. If , then and . Since the problem asks for x, write down its value, 1, and circle it. Then plug in and to every choice, and simplify: (A) –4.5 (B) –9 (C) 0.5 (D) 1 (E) 2

So the answer is (D).

2. Method 1: Plug in numbers. Let a be 100. If b is 20% greater than a, then . If c is 25% greater than b, then . The area of the largest square, then, is , and the area of the smallest square is . The percent difference is .

Method 2: Use algebra. and . So the area of the smallest square is a² and the area of the largest square is . Since , the area of the bigger square is 125% larger.

3. Method 1: Test the choices, starting with (C). If Ellen weighs 130 pounds, then Jim weighs pounds and Ria weighs pounds. All together, their weight would be pounds. Close, but too small. This means that our guess for Ellen”s weight is too big (because increasing Ellen”s weight decreases both Jim and Ria”s weight by the same amount, for a net decrease). This lets us eliminate choices (C), (D), and (E). Since our guess wasn”t far off, it makes sense to test choice (B) next. If Ellen weighs 120 pounds, then Jim weighs pounds and Ria weighs pounds. In total, they weigh. pounds. Bingo! The answer is (B).

Method 2: Use algebra. Let e = Ellen”s weight, j = Jim”s weight, and r = Ria”s weight Translate.

4. Method 1: Use algebra. Let x be the number of gallons of paint that she starts with. Translate the

The answer is (B).

Method 2: Test the choices. Look at the problem carefully. She uses one-fourth of her paint, then one-third of her paint, and is left with 10 gallons of paint, a whole number. This suggests that she started with a quantity that is divisible by 3 and 4. Since 24 is divisible by 3 and 4, it”s a good choice to test. One-fourth of 24 is 6, and one-third of 24 is 8. This means she would be left with . Bingo!

5. Method 1: Plug in. Let , so and . (Check that they “fit.”) Since the question asks for the value of s, write down 35 and circle it. Plugging these values into the choices gives (A) 140 (B) 35 (C) 136 (D) 124 (E) 280

The answer is (B).

Method 2: Use algebra. Solve the first equation for Then solve the second equation for r: . Then substitute: .