SAT Test Prep

CHAPTER 6
WHAT THE SAT MATH IS REALLY TESTING

Lesson 8: Checking Your Work

Check the Question

Always quickly reread the question before marking your answer to make sure that you”ve answered the right question and to make sure that your solution makes sense in the context of the question.

A bin contains 20 basketballs and soccer balls. If there are 8 more basketballs than soccer balls in the bin, how many soccer balls are in the bin?

(A) 4

(B) 6

(C) 8

(D) 10

(E) 12

Many students think that since there are 8 more basketballs than soccer balls, they should just subtract 8 from the total to get the number of soccer balls, getting soccer balls. The answer is (E), right?

Wrong. If there are 12 soccer balls, then there must be 8 basketballs, for a total of 20. But the question says that there are 8 more basketballs than soccer balls, and 8 sure isn”t more than 12! So now what? Eliminate choice (E) first of all. Since there are fewer basketballs than soccer balls, soccer balls must make up fewer than half the balls, so there must be fewer than 10 soccer balls, eliminating choice (D). Checking the remaining choices shows (B) 6 works because if there are 6 soccer balls, there are 14 basketballs, and 14 is 8 greater than 6!

The “direct” method for solving is to subtract 8 from 20 and then divide the result by 2 to get the number of soccer balls.

Check Your Algebra

When solving an equation, check two things: first your answer, and then your steps. If the answer works when you plug it back into the equation, there”s no need to check the steps. If it doesn”t, then check your steps. When solving equations, write out every step, and make sure that each one is logical. You”re likely to make mistakes if you skip steps or do them too quickly in your head.

If 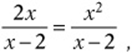then what is the value of x?

(A) 0

(B) 1

(C) 2

(D) 3

(E) 4

You might notice that since both fractions have the same numerator, the equation can be simplified and solved without much trouble.

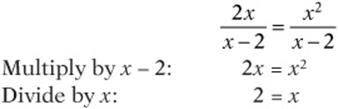
Piece of cake. The answer is (C), right? Wrong. Notice that substituting into the original equation gives you . Although this seems true at first, it”s not, because 4/0 isn”t a number! (Just ask your calculator.) What now? The check suggests a solution: you can just test the choices. Plugging in the other choices for x shows that only (A) 0 produces a true equation: .

What went wrong the first time? Check the steps. Our second step was to divide by x. We”re allowed to divide both sides of an equation by any number except 0 because division by 0 is undefined. That”s where we went wrong: We didn”t check division by 0. Notice that division by 0 also explains why x = 2 doesn”t work in the original equation.

Check by Estimating

Estimation is one of the simplest and most effective checking strategies you can use on the SAT. Getting an approximate answer can help you to narrow down the choices quickly.

If Carla drives at 40 miles per hour for n miles and then drives at 60 miles per hour for another n miles, what is her average speed, in miles per hour, for the entire trip?

(A) 42

(B) 48

(C) 50

(D) 52

(E) 54

Many students average 40 and 60 and get 50. But this is wrong because Carla is not spending equal times at 40 and 60 miles an hour. Since 40 mph is slower than 60 mph, she spends more time at that speed. So her average speed is closer to 40 than 60. This eliminates choices (C), (D), and (E). The correct answer is (B). (For more on rate problems, see Chapter 9, Lesson 4.)

Concept Review 8: Checking Your Work

1. What are the best strategies for avoiding mistakes when solving an equation?

2. When should you estimate on an SAT math question?

3. Why should you estimate on certain SAT math questions?

4. What is the last thing to check before marking an answer to an SAT math question?

5. What steps “aren”t allowed” when solving equations?

SAT Practice 8: Checking Your Work

Check your work carefully before choosing your answer to the following questions.

1. If , what is the value of ?

2. If , which of the following gives all possible values of s²?

(A) 2 only

(B) 4 only

(C) 0 and 2 only

(D) 0 and 4 only

(E) All even integers

3. Last year, Tom was twice as old as Julio. This year, the sum of their ages is 65. How old is Tom now?

(A) 22

(B) 32

(C) 41

(D) 42

(E) 43

4. If the 30 students in Ms. Harkin”s class scored an average of 80% on their final exams, and if the 20 students in Ms. Johnson”s class scored an average of 70% on their final exams, what was the average score for the two classes combined?

(A) 74%

(B) 75%

(C) 76%

(D) 77%

(E) 78%

5. What is the least positive integer m such that 168m is the square of an integer?

Answer Key 8: Checking Your Work

Concept Review 8

1. Check your answer by plugging it back into the original equation and checking your steps. Write out each step, one beneath the other, so that checking your logic and arithmetic is easier.

2. Estimate only when it is easy to do. If the answer choices are numerically far apart, estimation can help you to eliminate obviously wrong answers.

3. If you can quickly “ballpark” a numerical answer and rule out those choices that are “out of the ballpark,” you can often avoid doing complicated calculations or algebra.

4. Reread the question and make sure that you”ve answered the right question, and make sure that your answer makes sense in the context of the question.

5. Dividing by 0 and taking the square root of an expression that can be negative are not allowed because they are undefined.

SAT Practice 8

1. 30 The simplest way to solve this problem is to add 10 to both sides of the equation, which gives . However, many students do the “knee-jerk” of solving for x and become prone to silly arithmetic mistakes. If you did solve for x, you should have checked your answer by plugging it back in to the original equation.

2. D Did you say (C)? Then you misread the question. Always reread before marking your answer. It asks for the value of s², not s. Although s can be 0 or 2, s² is either 0 or 4. Did you say (A) or (B)? Then you may have made this common mistake:

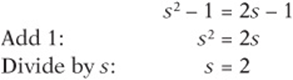
What went wrong? In the second step, we divided by s without checking whether it could equal 0. (Remember that division by 0 is undefined and usually causes trouble.) Indeed, plugging in shows that is in fact a solution. The correct method is

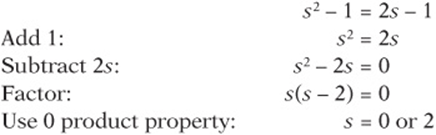
3. E You might start by approximating. Since the sum of their ages is about 60, and since Tom is about twice as old as Julio, Tom is about 40 and Julio is about 20. This rules out (A) and (B). From here, you may just want to “test” the remaining choices until you find what works. If you prefer algebra, you may want to let t equal Tom”s age now and j equal Julio”s age now. You are told that and that . Since you only need the value of t, solve the first equation for j, getting , and substitute this into the second equation. This gives

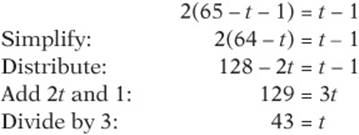
Therefore, Tom is now 43 and Julio is now . Notice that last year they were 42 and 21, respectively, and 42 is twice as old as 21.

4. C Since more students averaged 80% than 70%, the overall average should be closer to 80%. This rules out (A) and (B). To get the precise answer, let x be the overall average. There are two ways to calculate the sum of all the scores: and (50)(x). Since these must be equal,

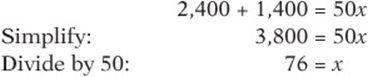
5. 42 Do the prime factorization of 168: . Since, in a perfect square, all prime factors “pair up,” we need to multiply at least one more factor of 2, one more factor of 3, and one more factor of 7 to make a perfect square: .(Notice that now every factor appears an even number of times.) Therefore, .