SAT Test Prep

CHAPTER 7
ESSENTIAL PRE-ALGEBRA SKILLS

Lesson 6: Negatives

Visualize the Number Line

Visualize the number line when comparing, adding, or subtracting numbers. Greater than always means to the right on the number line and less than means to the left on the number line. A negative number is greater than another if it is closer to 0.

Example:

Which is greater, –2/5 or –7/5? Answer: Visualize the number line. Although 2/5 is less than 7/5, on the negative side this relationship is “flipped.” –2/5 is closer to 0 than –7/5 is, so –2/5 is greater.

Adding and Subtracting with
Negatives

To add, visualize the number line. To add a positive, jump to the right. To add a negative, jump to the left.

Example:

To add , start at –5 and move 12 spaces to the left (negative), to land on –17.

((Or you could start at (–12 and jump 5 spaces to the left!)

To subtract, you can change the subtraction to addition by changing the sign of the second number.

Example:

To subtract , change it to addition by changing the sign of the second number: .

To subtract, you can also “swap” the numbers and change the sign of the result, because is the opposite of .

Example:

Remember these helpful facts about subtracting:

• is positive if a is greater than b and negative if b is greater than a (regardless of the signs).

• is always the opposite of .

Products, Quotients, and
Powers of Negatives

Any product, quotient, or power is negative if it has an odd number of negatives and positive if it has an even number of negatives.

Example:

is negative: it has an odd number (1) of negatives.

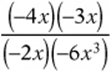is positive: it has an even number (4) of negatives.

is negative: it has an odd number of negatives.

Inequalities and Negatives

Any inequality must be “flipped” whenever you multiply or divide both sides by a negative.

Example:

Solve for x.

To isolate x, you must divide both sides by –3. But, since this changes the sign of both sides, you must “flip” the inequality, so the solution is .

Concept Review 6: Negatives

Write the correct inequality (< or >) in each space.

2.–10 _____ –25

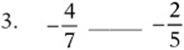
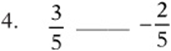
5. When does the expressions –x represent a positive number? _____________________________________________

6. An inequality must be “flipped” whenever ___________________________________________________________.

7. When is x – y negative? _____________________________________________________________________________

8. What is the simple way to tell quickly whether a product, quotient, or power is negative?

9. If , then . (Think before doing any algebra!)

Simplify the following expressions without a calculator.

10. If , then .

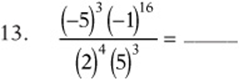
16. If , then

Solve the following inequalities for x:

SAT Practice 6: Negatives

1. For all real numbers b,

(A) –4b

(B) 4b

(C) b⁴

(D) –b⁴

(E) 4b⁴

2. If , then for which of the following values of m is k greater than 0?

(A) –2.47

(B) –1.47

(C) 0.47

(D) 1.47

(E) 2.47

3. For all real numbers w,

(A) –w⁴

(B) –2w²

(C) 0

(D) 2w²

(E) w⁴

4. If , which of the following must be true?

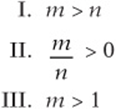
(A) I only

(B) II only

(C) III only

(D) I and II only

(E) I and III only

5. If and , then which of the following must be true?

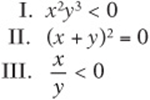
(A) III only

(B) I and II only

(C) II and III only

(D) I and III only

(E) I, II, and III

6. If and , then which of the following expressions must be negative?

(A) mn

(B) m²

(C) p⁵

(D) mp

(E) np

7. If and , then

(A) –4

(B) –3

(C) –2

(D) –1

(E) 0

8. If the sum of the integers from 15 to 50, inclusive, is equal to the sum of the integers from n to 50, inclusive, and , then

(A) –50

(B) –49

(C) –35

(D) –15

(E) –14

9. If and , then which of the following must be true?

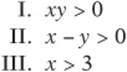
(A) II only

(B) I and II only

(C) II and III only

(D) I and III only

(E) I, II, and III

10. A sequence of numbers begins with the numbers –1, 1, 1, …, and each term afterward is the product of the preceding three terms. How many of the first 57 terms of this sequence are negative?

(A) 19

(B) 20

(C) 28

(D) 29

(E) 30

Answer Key 6: Negatives

Concept Review 6

1. <

2. >

3. <

4. >

5. Whenever x is negative.

6. You multiply or divide by a negative on both sides.

7. Whenever y is greater than x (regardless of sign).

8. If the number of negatives in the term is odd, then the result is negative. If the number of negatives in the term is even, then the result is positive. Remember to add the exponents of all the negative numbers in the term.

9. 10. Notice that is the opposite of . So is the opposite of .

10. –1. Notice that and must be opposites, and the quotient of non-zero opposites is always –1. (, , etc.)

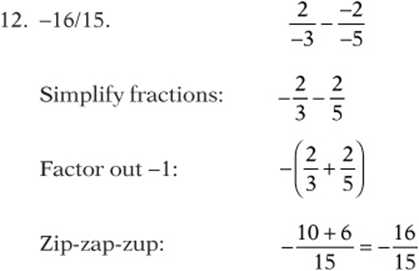
13. –1/16. Since there are an odd number (19) of negatives, the result is negative. Notice, too, that the powers of 5 cancel out.

14. –16

15. 35x¹⁷

16. only if (and so 2 –x is positive).

only if (and so 2 –x is negative).

SAT Practice 6

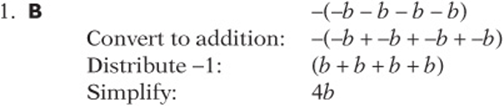
2. D Notice that . If the product is positive, then all three terms must be positive or one must be positive and the other two negative. They would all be positive only if , but no choice fits. If two terms are negative and one positive, then, by checking, .

3. B Don”t forget the order of operations: powers

4. B If m/n is positive, then m and n must have the same sign. Using and disproves statements I and III. Statement II must be true because m and n must have the same sign.

5. C The example and disproves statement I. Substituting –y for x (because an expression can always be substituted for its equal) and simplifying in statements II and III proves that both are true.

6. C Since m is negative, n⁴p⁵ must be negative because the whole product is positive. n can be either positive or negative; n⁴ will be positive in either case. Therefore, p⁵ must be negative.

7. D Since is always the opposite of ,.

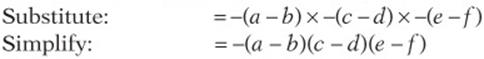
By comparing the two sides, x must equal –1.

8. E If the two sums are equal, then the sum of the integers from n to 14, which are not included in the first sum, must “cancel out.” That can only happen if n is –14.

9. C Simplify the first inequality by dividing both sides by –2. (Don”t forget to “flip” the inequality!) This gives . The example of and disproves statement I. Since x must be greater than y, statement II must be true. Since x is greater than 3.5, it must certainly be greater than 3, so statement III must be true.

10. D The sequence follows the pattern (–1, 1, 1,–1), (–1, 1, 1, –1), (–1, 1, 1, –1), …. Since the pattern is four terms long, it repeats times, with a remainder of 1 (the remainder shows that it includes the first term of the 15th repetition), which means it includes negatives.