SAT Test Prep

CHAPTER 7
ESSENTIAL PRE-ALGEBRA SKILLS

Lesson 7: Divisibility

Divisibility

There are five different ways of saying that one integer, a, is a multiple of another integer, b. Understand each phrasing.

• a is divisible by b.

• a is a multiple of b.

• b is a factor (divisor) of a.

• When a is divided by b, the remainder is 0.

• a/b is an integer.

Example:

42 is a multiple of 7, so

• 42 is divisible by 7.

• 42 is a multiple of 7.

• 7 is a factor (divisor) of 42.

• When 42 is divided by 7, the remainder is 0.

• 42/7 is an integer (6).

To see if integer a is divisible by integer b, divide a by b on your calculator and see whether the result is an integer. Or use one of the quick checks below.

• Multiples of 3 have digits that add up to a multiple of 3.

Example:

345 is a multiple of 3 because , which is a multiple of 3.

• Multiples of 5 end in 0 or 5.

• Multiples of 6 end in an even digit, and their digits add up to a multiple of 3.

• Multiples of 9 have digits that add up to a multiple of 9.

Example:

882 is a multiple of 9 because , which is an integer, and because its digit sum is a multiple of 9.

• If an integer is a multiple of 10, it ends in 0.

Remainders

A remainder is a whole number “left over” when one whole number is divided by another whole number a whole number of times.

Think about giving balloons to kids: you can only have a whole number of balloons, a whole number of kids, and you can”t give any kid a fraction of a balloon. If you try to divide 34 balloons among 4 kids, each kid can get 8 balloons, but then you will have 2 balloons “left over.” This is your remainder.

To find a remainder with a calculator, divide the two whole numbers on your calculator, then multiply the “decimal part” of the result by the divisor.

Example:

What is the remainder when 34 is divided by 5? and .

Remainders can be very useful in solving SAT “pattern” problems.

Example:

What is the 50th term in this sequence? 7, 9, 3, 1, 7, 9, 3, 1, …

The pattern repeats every four terms. The remainder when 50 is divided by 4 is 2, so the 50th term is the same as the 2nd term, which is 9.

Primes, Evens, and Odds

• A prime number is any integer greater than 1 that is divisible only by 1 and itself (like 2, 3, 5, 7, 11, 13, 17, …).

• An even number is any multiple of 2. It can always be expressed as 2n, where n is some integer. e.g.,

• An odd number is any integer that is not a multiple of 2. Any odd number can be expressed as , where n is some integer. e.g., .

Be careful not to confuse odd with negative (and even with positive). Students commonly do this because odd and negative are “bad” words and even and positive are “good” words. To avoid this mistake, pay special attention to the words odd, even, negative, and positive by underlining them when you see them in problems.

Concept Review 7: Divisibility

1. What is a prime number? _________________________________________

2. What is a remainder? _________________________________________

3. An odd number is _________________________________________ and can always be expressed as ________________________________________.

4. What can you do to avoid confusing odd with negative or even with positive? ______________________________

5. How do you find a remainder with your calculator? _________________________________________

6. If an integer is divisible by k, 12, and 35, and k is a prime number greater than 7, then the integer must also be divisible by which of the following? (Circle all that apply.)

7. When a whole number is divided by 7, what are the possible remainders? ______________________________

15. If z is an integer, which of the following must be odd? (Circle all that apply.)

16. If a divided by b leaves a remainder of r, then a must be __________ greater than a multiple of __________.

SAT Practice 7: Divisibility

1. When an integer n is divided by 10, the remainder is 7. What is the remainder when n is divided by 5?

2. When 8 is divided by 12, the remainder is

(C) 4

(D) 8

(E) 12

3. If p is odd and q is even, then which of the following must be an odd number?

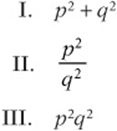
(A) none

(B) I only

(C) I and II only

(D) I and III only

(E) I, II, and III

4. 1, 3, 5, 7, 9, 1, 3, 5, 7, 9, 1, …

If the sequence above follows the pattern shown, what is the 103rd term of the sequence?

(A) 1

(B) 3

(C) 5

(D) 7

(E) 9

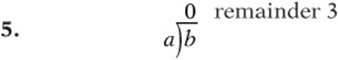
In the division problem shown above, if a and b are positive, which of the following must be true?

6. Which of the following is a counterexample to the statement: All prime numbers are odd?

(A) 2

(B) 3

(C) 9

(D) 11

(E) 12

7. If and are both positive integers, then which of the following must also be an integer?

8. If a, b, c, d, and e are consecutive integers, then which of the following statements must be true?

I. This set contains 3 odd numbers.

II. This set contains a number divisible by 5.

is odd.

(A) I only

(B) II only

(C) I and II only

(D) I and III only

(E) I, II, and III

9. m and n are positive integers. If m is divided by n, the quotient is 7 with a remainder of 4. Which of the following expresses m in terms of n?

10. If a and b are positive integers and , then which of the following must be true?

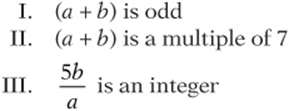
(A) II only

(B) I and III only

(C) I and II only

(D) I and III only

(E) I, II, and III

Answer Key 7: Divisibility

Concept Review 7

1. Any integer greater than 1 that is divisible only by 1 and itself.

2. The whole number “left over” when one whole number is divided by another whole number a whole number of times.

3. Any integer that is not divisible by 2. .

4. Underline and think about those words when you see them in problems.

5. Divide the two integers, then multiply the decimal part of the result by the divisor (the number you divided by).

6. The least common multiple of k, 12, and 35 is 420k, which is divisible by 3k, 10, 28k, 2, and 35 k.

7. 0, 1, 2, 3, 4, 5, and 6.

8. 3. The pattern is 3 terms long, and 3 divided by 100 has a remainder of 1, so the 100th term is the same as the 1st.

9. 1.

10. 64. The number must be 1 greater than both a multiple of 7 and a multiple of 9. The only multiple of 7 and 9 that is between 1 and 100 is 63, and .

11. 1/2. The sequence is

1, 2, 2, 1, 1/2, 1/2, 1, 2, 2, 1, 1/2, 1/2, …, so the pattern is 6 terms long. 65 divided by 6 leaves a remainder of 5, so the 65th term is the same as the 5th, which is 1/2.

12. 1.

13. 5. The least common multiple of 6 and 9 is 18, and …, which means that there are 5 multiples of 18 between 1 and 100.

14. None. Prime numbers are divisible only by themselves and 1, but any multiple of 6 must also be divisible by 2 and 3.

15. and are the only expressions that must be odd. Since 4 is even, 4z is even, so must be odd. , and since either z or must be even, is even and is odd.

16. If a divided by b leaves a remainder of r, then a must be r greater than a multiple of b.

SAT Practice 7

1. 2 Since n leaves a remainder of 7 when divided by 10, it must be 7 more than a multiple of 10, like 7, 17, 27, etc. When any of these is divided by 5, the remainder is 2.

2. D Don”t confuse remainder with quotient. Remember to think of balloons and kids. If you had 8 balloons to divide among 12 kids, you”d have to keep all 8 balloons because there aren”t enough to go around fairly. Also, you can use the calculator method, and divide 8 by 12, then multiply the decimal part of the result by 12.

3. B Using and rules out II (1/4 is not an integer, let alone an odd number) and III (4 is even). will always be odd, because the square of an odd is always odd and the square of an even is always even, and an odd plus an even is always odd.

4. C The sequence that repeats is 5 terms long. 103 divided by 5 leaves a remainder of 3, so the 103rd term is the same as the 3rd term, which is 5.

5. D For the statement to be correct, , so .

6. A A counterexample to the statement All prime numbers are odd would be a prime number that is not odd. The only even prime number is 2.

7. A If and are both positive integers, then k must be a common multiple of 7 and 12. The least common multiple of 7 and 12 is 84. If we substitute 84 for k, (A) is the only choice that yields an integer.

8. D Using the example of 2, 3, 4, 5, 6 disproves statement I. Since multiples of 5 occur every 5 consecutive integers, II must be true (remember that 0 is a multiple of every integer, including 5). Since bc will always be an even times an odd or an odd times an even, the result must always be even, so must be odd.

9. E You might simplify this problem by picking values for m and n that work, like 46 and 6. (When 46 is divided by 6, the quotient is 7 with a remainder of 4.) If we substitute 6 for n, choice (E) is the only one that yields 46.

10. D Using and disproves statement I. If a/b equals 5/2 and a and b are both integers, then and , where k is an integer. Therefore so II is true. Also, since a/b equals 5/2, , so , which is an integer, so III is true.