SAT Test Prep
CHAPTER 8
ESSENTIAL ALGEBRA I SKILLS
1. Solving Equations
2. Systems
3. Working with Exponentials
4. Working with Roots
5. Factoring
6. Inequalities, Absolute Values, and Plugging In
7. Word Problems

Lesson 1: Solving Equations
Equations as Balanced Scales
Algebra is really common sense once you start thinking of every equation as a balanced scale. The terms on either side of the equals sign must be “balanced,” just like the weights on a scale.
The laws of equations come from the commonsense rules for keeping a scale balanced. Imagine that you are the keeper of a scale, and you must keep it balanced. What would you do if someone took weights from one side of the scale? You”d remove an equal weight from the other side, of course. This is a law of equality: anything you do to one side of the equation, you must do to the other to maintain the balance.
Example:
If ![]() , then what is the value of
, then what is the value of ![]()
Don”t worry about solving for x, because that”s not what the question is asking for. Notice that the expression you are given, ![]() , is 4 times the expression you are looking for, 3x – 2. So to turn the given expression into the one you want, divide by 4. Of course, you must do the same to the other side to keep the balance:
, is 4 times the expression you are looking for, 3x – 2. So to turn the given expression into the one you want, divide by 4. Of course, you must do the same to the other side to keep the balance:
![]()
Solving as Unwrapping
Solving simple algebraic equations is basically the same thing as unwrapping a present. (And it”s just as fun, too, right? Okay, maybe not.) Wrapping a present involves a sequence of steps: 1. Put the gift in the box. 2. Close the box. 3. Wrap the paper around the box. 4. Put the bow on. Here”s the important part: unwrapping the present just means inverting those steps and reversing their order: 1. Take off the bow. 2. Unwrap the paper. 3. Open the box. 4. Take out the gift.
Example:
![]()
The problem is that x is not alone on the left side; it is “wrapped up” like a gift. How is it wrapped? Think of the order of operations for turning x into ![]() :
:
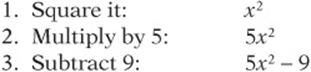
So to “unwrap” it, you reverse and invert the steps:
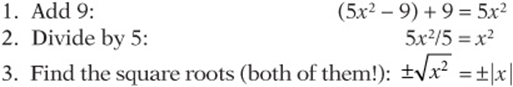
If you perform these steps to both sides, ![]() transforms into
transforms into ![]()
Watch Your Steps
To solve that last equation, we had to perform three operations. Many equations, as you probably know, require more steps to solve. It is very important that you keep track of your steps so that you can check your work if you need to. In other words, the equation we just solved should really look like this on your scratch paper:

Check by Plugging Back In
Always check your answer by plugging it back into the original equation to see if it works. Remember that solving an equation means simply finding the value of each unknown that makes the equation true.
Example:
Are ![]() solutions to
solutions to ![]() Plug them in:
Plug them in: ![]()
There”s a lot of detail to learn and understand to do well on the SAT. For more tools and resources that will help, visit our Online Practice Plus at www.MHPracticePlus.com/SATmath.
Concept Review 1: Solving Equations
1. Explain the laws of equality.
2. Are there any operations you can perform to both sides of an equation that will not yield a true equation? Explain.
Show your steps and check your work in solving the following equations.
![]()
![]()
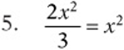
![]()
Solve the following equations for the given expression by performing one operation on both sides.

SAT Practice 1: Solving Equations
1. If ![]() , then
, then ![]()
(A) – 24
(B) – 12
(C) 0
(D) 12
(E) 24
2. What number decreased by 7 equals 5 times the number?
![]()
![]()
![]()
![]()
![]()
3. If 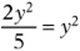 , then
, then ![]()

4. If ![]() , then
, then ![]()
(A) –54
(B) –6
(C)18
(D)36
(E)54
![]()
5. The equation above is true for which of the following values of p?
(A) –2 and 5
(B) 2 and –5
(C) 0 and 1
(D) 1.5 only
(E) 3.5 only
6. if ![]() what is the value of x?
what is the value of x?
![]()
(B) –7
![]()
![]()
(E) 7
7. The product of x and y is 36. If both x and y are integers, then what is the least possible value of x-y?
(A) –37
(B) –36
(C) –35
(D) –9
(E) –6
8. The graph of ![]() contains the points (–1, 7) and (1, 3). Which of the following could be f (x)?
contains the points (–1, 7) and (1, 3). Which of the following could be f (x)?
![]()
![]()
![]()
(A) I only
(B) I and II only
(C) I and III only
(D) I and III only
(E) I, II, and III
9. If ![]() , which of the following gives all possible values of x?
, which of the following gives all possible values of x?
(A) 9 only
(B) –9 and 9
(C) 81 only
(D) 81 and –81
(E) 961
10. For all positive values of m and n, if ![]() , then x =
, then x =
![]()
![]()
![]()
![]()
![]()
Answer Key 1: Solving Equations
Concept Review 1
1. The laws of equality say that whatever you do to one side of an equation you must do to the other side, to maintain the balance.
2. Yes. Dividing by 0 and taking the square root of a negative number are “undefined” operations in the real numbers. Be careful, then, when dividing both sides of an equation by an unknown, to check that the unknown could not possibly be 0.



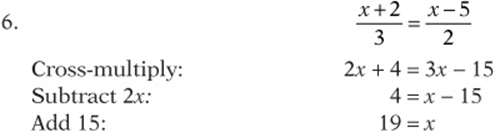
7. Operation: Multiply both sides by 4 Solution: ![]()
8. Operation: Divide both sides by 3 Solution: ![]()
SAT Practice 1
![]()
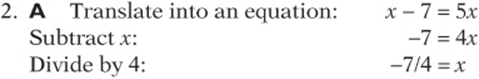
You can also “test” the choices and see which one works, but that”s probably more time-consuming.
3. 5 It”s easiest to solve the equation for y, then add 5


5. D Plugging in and checking is perhaps easiest here, but you could do the algebra too:
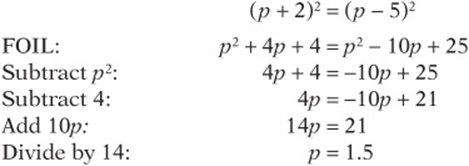
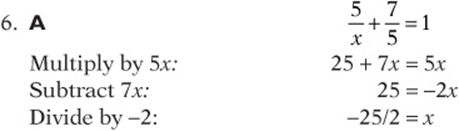
7. C Guess and check here. If ![]() and
and ![]() , or
, or ![]() and
and ![]() , then
, then ![]() .
.
8. E Just plug in the points (–1, 7) and (1, 3) to the equations, and confirm that the points “satisfy” all three equations.

