SAT Test Prep
CHAPTER 9
SPECIAL MATH PROBLEMS
1. New Symbol or Term Problems
2. Mean/Median/Mode Problems
3. Numerical Reasoning Problems
4. Rate Problems
5. Counting Problems
6. Probability Problems

Lesson 1: New Symbol or Term Problems
New Symbol or Term Problems
Don”t be intimidated by SAT questions with strange symbols, like Δ, ϕ, or ¥, or new terms that you haven”t seen before. These crazy symbols or terms are just made up on the spot, and the problems will always explain what they mean. Just read the definition of the new symbol or term carefully and use it to “translate” the expressions with the new symbol or term.
Example:
Let the “kernel” of a number be defined as the square of its greatest prime factor. For instance, the kernel of 18 is 9, because the greatest prime factor of 18 is 3 (prime factorization: ![]() , and 32 equals 9.
, and 32 equals 9.
Question 1: What is the kernel of 39?
Don”t worry about the fact that you haven”t heard of a “kernel” before. Just read the definition carefully. By the definition, the kernel of 39 is the square of its greatest prime factor. So just find the greatest prime factor and square it. First, factor 39 into 3 × 13, so its greatest prime factor is 13, and ![]() .
.
Question 2: What is the greatest integer less than 20 that has a kernel of 4?
This requires a bit more thinking. If a number has a kernel of 4, then 4 must be the square of its greatest prime factor, so its greatest prime factor must be 2. The only numbers that have a greatest prime factor of 2 are the powers of 2. The greatest power of 2 that is less than 20 is ![]() .
.
Example:
For all real numbers a and b, let the expression ![]() be defined by the equation
be defined by the equation ![]() .
.
Question 3: What is ![]()
Just substitute 5 for a and 10 for b in the given equation: ![]() .
.
Question 4: If ![]() , what is the value of x?
, what is the value of x?
Just translate the left side of the equation:
Then solve for x: 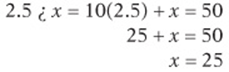
Question 5: What is 1.5 ¿ (1.5 ¿ 1.5)?
According to the order of operations, evaluate what is in parentheses first:

Concept Review 1: New Symbol or Term Problems
For questions 1–6, translate each expression into its simplest terms, using the definition of the new symbol.
The following definition pertains to questions 1–3:
For any real number x, let §x be defined as the greatest integer less than or equal to x.
![]()
![]()
![]()
The following definition pertains to questions 4–6:
If q is any positive real number and n is an integer, let q @ n be defined by the equation ![]()
![]()
![]()
![]()
7. If q is any positive real number and n is an integer, let q @ n be defined by the equation ![]()
If ![]() , what is the value of y?
, what is the value of y?
8. For any integer n and real number x, let x ^ n be defined by the equation ![]() . If
. If ![]() , what is the value of y?
, what is the value of y?
9. For any integer n, let Ωn be defined as the sum of the distinct prime factors of n. For instance, ![]() , because 2 and 3 are the only prime factors of 36 and
, because 2 and 3 are the only prime factors of 36 and ![]() . What is the smallest value of w for which
. What is the smallest value of w for which ![]()
SAT Practice 1: New Symbol or Term Problems
1. For all real numbers d, e, and f, let ![]() . If
. If ![]() , then x =
, then x =
![]()
![]()
![]()
(D) 2
(E) 6
2. If ![]() , let
, let 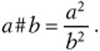 If
If ![]() , then which of the following statements must be true?
, then which of the following statements must be true?
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) x and y are both positive
3. On a digital clock, a time like 6:06 is called a “double” time because the number representing the hour is the same as the number representing the minute. Other such “doubles” are 8:08 and 9:09. What is the smallest time period between any two such doubles?
(A) 11 mins.
(B) 49 mins.
(C) 60 mins.
(D) 61 mins.
(E) 101 mins.
4. Two numbers are “complementary” if their reciprocals have a sum of 1. For instance, 5 and ![]() are complementary because
are complementary because ![]()
If x and y are complementary, and if ![]() what is y?
what is y?
(A) –2
![]()
![]()
![]()
(E) 3
5. For ![]() , let
, let ![]() What is the value of $$5?
What is the value of $$5?

6. For all nonnegative real numbers x, let ![]() be defined by the equation
be defined by the equation 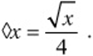 For what value of x does
For what value of x does ![]()
(A) 0.3
(B) 6
(C) 12
(D) 14
(E) 36
7. For any integer n, let [n] be defined as the sum of the digits of n. For instance, ![]() . If a is an integer greater than 0 but less than 1,000, which of the following must be true?
. If a is an integer greater than 0 but less than 1,000, which of the following must be true?
![]()
![]()
III. If a is even, then [a] is even
(A) none
(B) II only
(C) I and II only
(D) I and III only
(E) I, II, and III
8. For all integers, n, let 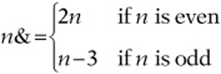 What is the value of 13&&?
What is the value of 13&&?
(A) 10
(B) 13
(C) 20
(D) 23
(E) 26
Answer Key 1: New Symbol or Term Problems
Concept Review 1
![]()
![]()
![]()
![]()
![]()
![]()


9. If ![]() , then w must be a number whose distinct prime factors add up to 12. The prime numbers less than 12 are 2, 3, 5, 7, and 11. Which of these have a sum of 12? (Remember you can”t repeat any, because it says the numbers have to be distinct.) A little trial and error shows that the only possibilities are 5 and 7, or 2, 3, and 7. The smallest numbers with these factors are
, then w must be a number whose distinct prime factors add up to 12. The prime numbers less than 12 are 2, 3, 5, 7, and 11. Which of these have a sum of 12? (Remember you can”t repeat any, because it says the numbers have to be distinct.) A little trial and error shows that the only possibilities are 5 and 7, or 2, 3, and 7. The smallest numbers with these factors are ![]() and
and ![]() . Since the question asks for the least such number, the answer is 35.
. Since the question asks for the least such number, the answer is 35.
SAT Practice I
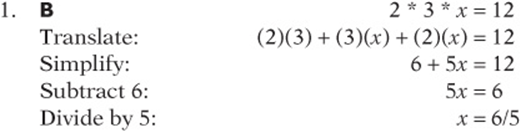
2. D If ![]() , then
, then ![]() , which means
, which means ![]() . Notice that
. Notice that ![]() and
and ![]() is one possible solution, which means that
is one possible solution, which means that
![]()
![]()
(E) x and y are both positive is not necessarily true. Another simple solution is ![]() and
and ![]() , which means that
, which means that
![]() is not necessarily true, leaving only
is not necessarily true, leaving only
(D) as an answer.
3. B All of the consecutive “double times” are 1 hour and 1 minute apart except for 12:12 and 1:01, which are only 49 minutes apart.
4. A If ![]() and y are complementary, then the sum of their reciprocals is 1:
and y are complementary, then the sum of their reciprocals is 1:
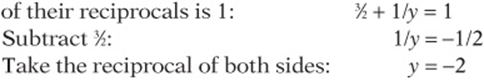
5. 5 The “double” symbol means you simply perform the operation twice. Start with 5, then ![]() . Therefore,
. Therefore, ![]() .
.
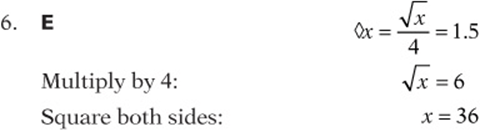
Plug in x = 36 to the original and see that it works.
7. C If a is 12, which is even, then ![]() is odd, which means that statement III is not necessarily true. (Notice that this eliminates choices (D) and (E).) Statement I is true because [10a] will always equal [a] because 10a has the same digits as a, but with an extra 0 at the end, which contributes nothing to the sum of digits. Therefore,
is odd, which means that statement III is not necessarily true. (Notice that this eliminates choices (D) and (E).) Statement I is true because [10a] will always equal [a] because 10a has the same digits as a, but with an extra 0 at the end, which contributes nothing to the sum of digits. Therefore, ![]() is always true. Notice that this leaves only choice (C) as a possibility. To check statement II, though (just to be sure!), notice that the biggest sum of digits that you can get if a is less than 1,000 is from 999.
is always true. Notice that this leaves only choice (C) as a possibility. To check statement II, though (just to be sure!), notice that the biggest sum of digits that you can get if a is less than 1,000 is from 999. ![]() ; therefore,
; therefore, ![]() . It”s possible to get a slightly bigger value for [[a]] if a is, say,
. It”s possible to get a slightly bigger value for [[a]] if a is, say, ![]() , but you can see that [[a]] will never approach 20.
, but you can see that [[a]] will never approach 20.
8. C Since 13 is odd, ![]() . Therefore,
. Therefore, ![]() ;. Since 10 is even,
;. Since 10 is even, ![]() .
.