SAT Test Prep
CHAPTER 9
SPECIAL MATH PROBLEMS
Lesson 3: Numerical Reasoning Problems
Arithmetic Reasoning
Some of the most common problems on the SAT are numerical reasoning problems, which ask you to think about what happens to numbers when you perform basic operations on them. You just need to know the common numerical and arithmetic rules and think logically.
Example:
If a + b is negative, which of the following CANNOT be negative?
(A) ab
(B) ab2
(C) a2b
(D) a2b2
![]()
Start by thinking about what might be true about a and b and what must be true about a and b. First think of possible values for a and b. –2 and 1 work, because ![]() . Notice that this proves that (A), (B), and (E) are incorrect, because they can be negative:
. Notice that this proves that (A), (B), and (E) are incorrect, because they can be negative: ![]() ,
,![]() , and
, and ![]() . But
. But ![]() is positive, so does that mean the answer is (C)? Not so fast! Your job is not to find which one can be positive, but rather which cannot be negative. Notice that (C) can be negative if a and b are, say, 1 and –2 (notice that
is positive, so does that mean the answer is (C)? Not so fast! Your job is not to find which one can be positive, but rather which cannot be negative. Notice that (C) can be negative if a and b are, say, 1 and –2 (notice that ![]() is still negative, so those values work):
is still negative, so those values work): ![]() . Therefore, by process of elimination, the answer is (D).
. Therefore, by process of elimination, the answer is (D).
This question is much easier if you remember a simple fact: If x is a real number, then x2 is never negative. If you don”t know this already, play around with possible values of x until you see why this is true. Then look at choice (D) a2b2. a2 can”t be negative, and neither can b2, so a2b2 can”t be negative.
Example:
If ![]() ,
, ![]() , and
, and ![]() , then which of the following must be true?
, then which of the following must be true?
I. If m and n are negative, then ![]() .
.
II. ![]()
III. ![]()
(A) I only
(B) II only
(C) I and II only
(D) I and III only
(E) I, II, and III
The first statement, ![]() , tells you that the alphabetical order is also the numerical order of the numbers. The second statement, mnpr = 0, tells you that one of the numbers must be 0. (This is the zero product property!) The third statement,
, tells you that the alphabetical order is also the numerical order of the numbers. The second statement, mnpr = 0, tells you that one of the numbers must be 0. (This is the zero product property!) The third statement, ![]() , tells you that you must have at least one positive and one negative, and all the numbers must “cancel out.” This means that m can”t be 0 because then none of the numbers would be negative, and r can”t be 0, because then none of the numbers would be positive. Thus, either n or p is 0. This means that both I and II are necessarily true, so you can eliminate choices (A), (B), and (D). The example
, tells you that you must have at least one positive and one negative, and all the numbers must “cancel out.” This means that m can”t be 0 because then none of the numbers would be negative, and r can”t be 0, because then none of the numbers would be positive. Thus, either n or p is 0. This means that both I and II are necessarily true, so you can eliminate choices (A), (B), and (D). The example ![]() ,
, ![]() ,
, ![]() ,
, ![]() shows that statement III is not necessarily true, so the answer is (C).
shows that statement III is not necessarily true, so the answer is (C).
Digit Problems
You may see a question on the SAT like the one below, where letters represent digits. Remember that digits can only take the values 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. Also remember that you may have to consider “carried” digits when looking at a sum or product. Lastly, you may find it best to work from left to right rather than right to left.
Example:
![]()
If A and B represent distinct digits in this addition problem, what is the value of A – B?
(A) –9
(B) –7
(C) 2
(D) 7
(E) 9
Look at the left (hundreds) column first. Since the sum has a 2 in the hundreds place, there must be a carry of 1 from the tens place. Therefore, ![]() (carry from ones column, if any) = (11. This means
(carry from ones column, if any) = (11. This means ![]() or 3. Trying each one shows that only
or 3. Trying each one shows that only ![]() and
and ![]() works, giving
works, giving ![]() . Therefore
. Therefore ![]() , so the answer is (D).
, so the answer is (D).
Concept Review 3: Numerical Reasoning Problems
1. If neither a nor b is 0, what is the relationship between ![]() and
and ![]() ?
?
2. What is the relationship between ![]() and
and ![]() ?
?
Complete the following “parity rules.”
3. Odd × even _____
4. Even × even _____
5. Odd × odd _____
6. Even + even _____
7. Odd + even _____
8. Odd + odd _____
Complete the following “sign rules.”
9. If n is odd, ![]() .
.
10. If n is even, ![]() i.
i.
11. If ![]() and
and ![]() , then
, then ![]()
12. Dividing by x is the same as multiplying by __________.
13. Subtracting ![]() is the same as adding __________.
is the same as adding __________.
14. When a number is multiplied by its reciprocal, the result is __________.
15. When a number and its opposite are added, the result is __________.
16. When a number (other than 0) is divided by its opposite, the result is __________.
17. If a positive number is multiplied by a number greater than 1, what happens to it? _______________
18. If a positive number is multiplied by a number between 0 and 1, what happens to it? _______________
19. If a negative number is multiplied by a number greater than 1, what happens to it? _______________
20. Is x always bigger than –x? Explain.
21. Is x2 always bigger than x? Explain.
22. Is x3 always bigger than x2? Explain.
23. If x is between 0 and 1, then 1/x is _________________________.
24. If ![]() , then
, then ![]() is ____________________.
is ____________________.
25. If ![]() , then
, then ![]() is ____________________.
is ____________________.
SAT Practice 3: Numerical Reasoning Problems
1. If m and n are both odd integers, which of the following must be true?
![]() is even
is even
![]() is divisible by 4
is divisible by 4
![]() is divisible by 4
is divisible by 4
(A) none
(B) I only
(C) I and II only
(D) I and III only
(E) I, II, and III

If A and B represent distinct digits in this correctly worked multiplication problem, what is the value of B?
(A) 2
(B) 3
(C) 5
(D) 6
(E) 8
3. If j is the number of integers between 1 and 500 that are divisible by 9 and k is the number of integers between 1 and 500 that are divisible by 7, what is ![]() ?
?
(A) 126
(B) 127
(C) 128
(D) 129
(E) 130
4. If 60 is written as the product of four integers, each greater than 1, then what is the sum of those integers?

5. If n is an integer and 2n is a factor of ![]() , what is the greatest possible value of n?
, what is the greatest possible value of n?
(A) 5
(B) 6
(C) 7
(D) 8
(E) 9
6. If ![]() is 4 times
is 4 times ![]() , and
, and ![]() , which of the following has exactly one possible value?
, which of the following has exactly one possible value?
(A) p
(B) q
(C) pq
![]()
![]()
7. If a, b, c, d, and e are whole numbers and ![]() is odd, then which of the following CANNOT be even?
is odd, then which of the following CANNOT be even?
(A) a
(B) b
(C) c
(D) d
(E) e
![]()
8. If each letter in the sums above represents a different positive integer, then ![]()
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
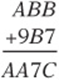
9. If A, B, and C are distinct digits in the correctly worked addition problem above, what is the value of ![]() ?
?
(A) 4
(B) 9
(C) 14
(D) 16
(E) 17
Answer Key 3: Numerical Reasoning Problems
Concept Review 3
1. They are reciprocals, so their product is 1.
2. They are opposites, so their sum is 0.
3. Odd × even = even
4. Even + even = even
5. Odd × odd = odd
6. Even + even = even
7. Odd + even = odd
8. Odd + odd = even
9. If n is odd, ![]() .
.
10. If n is even, ![]() .
.
11. If ![]() and
and ![]() , then
, then ![]() .
.
12. Dividing by x is the same as multiplying by 1/x.
13. Subtracting ![]() is the same as adding
is the same as adding ![]() .
.
14. When a number is multiplied by its reciprocal, the result is 1.
15. When a number and its opposite are added, the result is 0.
16. When a number (other than 0) is divided by its opposite, the result is –1.
17. It gets bigger.
18. It gets smaller.
19. It gets smaller (more negative).
20. No. If x is 0, then –x is equal to x, and if x is negative, then a –x is greater than x.
21. No. If x is between 0 and 1, then x2 is smaller than x. And if x is 0 or 1, then they are the same. If x is negative, then x2 is positive, and therefore greater than x.
22. No. If x is between 0 and 1, then x3 is smaller than x2. And if x is 0 or 1, then they are the same. If x is negative, then x2 is positive, and therefore greater than x3.
23. greater than 1.
24. greater than 1.
25. between 0 and 1.
SAT Practice 3
1. D Start with the simplest odd values for m and ![]() . (There”s no reason why m and n can”t equal the same number!) Notice that
. (There”s no reason why m and n can”t equal the same number!) Notice that ![]() , which isn”t divisible by 4, so statement II is not necessarily true, and you can eliminate choices (C) and (E). Next, notice thatm2 and n2 must both be odd, so m2 + n2 must be even, so statement I is necessarily true, and you can eliminate choice (A).
, which isn”t divisible by 4, so statement II is not necessarily true, and you can eliminate choices (C) and (E). Next, notice thatm2 and n2 must both be odd, so m2 + n2 must be even, so statement I is necessarily true, and you can eliminate choice (A). ![]() must be a multiple of 4 because m + n must be even (odd + odd = even), so it is a multiple of 2. When it is squared, it becomes a multiple of 4. So III is true, and the answer is (D).
must be a multiple of 4 because m + n must be even (odd + odd = even), so it is a multiple of 2. When it is squared, it becomes a multiple of 4. So III is true, and the answer is (D).
2. D Trial and error should show that ![]() . If A is less than 3, the product is too small. If A is greater than 3, the product is too large. Since
. If A is less than 3, the product is too small. If A is greater than 3, the product is too large. Since ![]() ,
, ![]() .
.
3. A ![]() , so there are 55 multiples of 9 between 1 and 500.
, so there are 55 multiples of 9 between 1 and 500. ![]() , so there are 71 multiples of 7 between 1 and 500. So
, so there are 71 multiples of 7 between 1 and 500. So ![]() .
.
4. 12 Trial and error shows that the only way to write 60 as the product of four integers, each greater than 1, is ![]() . Their sum is
. Their sum is ![]() .
.
5. C Do the prime factorization:
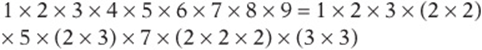
Since there are seven factors of 2, the greatest power of 2 that is a factor is 27.

(This is okay as long as p is anything but 0.)

Because p can have many possible values but q can only equal 3/5, (B) q is the only expression that has only one possible value.
7. A a cannot be even, because an even number times any other integer yields an even number, but ![]() is odd.
is odd.
8. A The only three different positive integers that have a sum of 7 are 1, 2, and 4. The only three different positive integers that have a sum of 9 are 1, 3, and 5 or 1, 2, and 6. But ![]() doesn”t work, since that would have two numbers in common with the first set, but it may only have one (C). Since (C) is the only number they may have in common, it must be 1.
doesn”t work, since that would have two numbers in common with the first set, but it may only have one (C). Since (C) is the only number they may have in common, it must be 1.
9. C The only solution is ![]() , so
, so ![]() .
.