SAT Test Prep

CHAPTER 10
ESSENTIAL GEOMETRY SKILLS

Lesson 2: Triangles

Angles in Polygons

Remembering what you learned about parallel lines in the last lesson, consider this diagram:

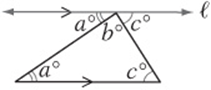
We drew line ℓ so that it is parallel to the opposite side of the triangle. Do you see the two Z”s? The angles marked a are equal, and so are the angles marked c. We also know that angles that make up a straight line have a sum of 180°, so . The angles inside the triangle are also a, b, and c.

Therefore, the sum of angles in a triangle is always 180°.

Every polygon with n sides can be divided into n – 2 triangles that share their vertices (corners) with the polygon:

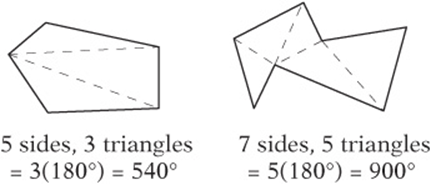
Therefore, the sum of the angles in any polygon with n sides is 180(n – 2) °.

Angle-Side Relationships in Triangles

A triangle is like an alligator mouth with a stick in it: The wider the mouth, the bigger the stick, right?

Therefore, the largest angle of a triangle is always across from the longest side, and vice versa. Likewise, the smallest angle is always across from the shortest side.

Example:

In the figure below, , so

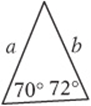
An isosceles triangle is a triangle with two equal sides. If two sides in a triangle are equal, then the angles across from those sides are equal, too, and vice versa.

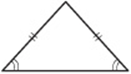
The Triangle Inequality

Look closely at the figure below. The shortest path from point A to point B is the line segment connecting them. Therefore, unless point C is “on the way” from A to B, that is, unless it”s on , the distance from A to B through C must be longer than the direct route. In other words:

The sum of any two sides of a triangle is always greater than the third side. This means that the length of any side of a triangle must be between the sum and the difference of the other two sides.

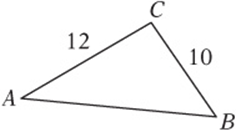
The External Angle Theorem

The extended side of a triangle forms an external angle with the adjacent side. The external angle of a triangle is equal to the sum of the two “remote interior” angles. Notice that this follows from our angle theorems:

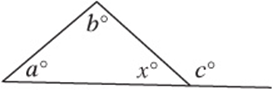
and ; therefore,

Concept Review 2: Triangles

1. The sum of the measures of the angles in a quadrilateral is __________.

2. The sum of the measures of the interior angles in an octagon is __________.

3. In ΔABC, if the measure of ∠A is 65° and the measure of ∠B is 60°, then which side is longest? __________.

4. The angles in an equilateral triangle must have a measure of __________.

5. Can an isosceles triangle include angles of 35° and 60°? Why or why not?

6. Draw a diagram to illustrate the external angle theorem.

7. If a triangle has sides of lengths 20 and 15, then the third side must be less than __________ but greater than __________.

8. Is it possible for a triangle to have sides of lengths 5, 8, and 14? Why or why not?

9. If an isosceles triangle includes an angle of 25°, the other two angles could have measures of __________ and __________ or __________ and __________.

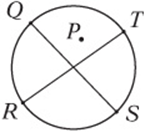
10. In the figure above, and are diameters of the circle and P is not the center. Complete the statement below with <, >, or=.

SAT Practice 2: Triangles

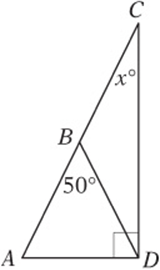
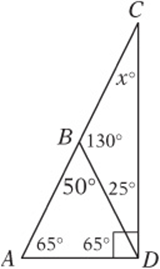
1. In the figure above, if , then x =

(A) 25

(B) 30

(C) 35

(D) 50

(E) 65

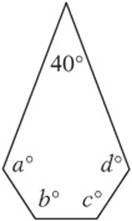
2. In the figure above,

3. The three sides of a triangle have lengths of 9, 16, and k. Which of the following could equal k?

I. 6

II. 16

III. 25

(A) I only

(B) II only

(C) I and II only

(D) I and III only

(E) I, II, and III

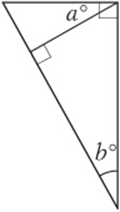
Note: Figure not drawn to scale.

4. Which of the following statements about a and b in the figure above must be true?

(A) I only

(B) II only

(C) I and II only

(D) I and III only

(E) I, II, and III

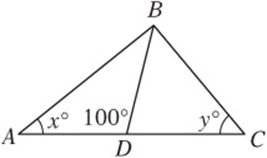
5. In the figure above, if , then

(A) 70

(B) 80

(C) 90

(D) 100

(E) 120

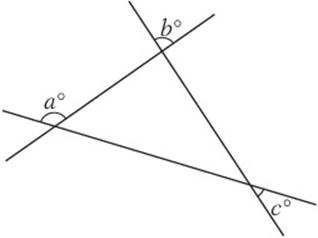
6. In the figure above, which of the following expresses a in terms of b and c?

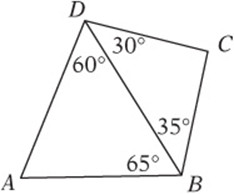
Note: Figure not drawn to scale.

7. Which of the following represents the correct ordering of the lengths of the five segments in the figure above?

8. A triangle has two sides of lengths 4 centimeters and 6 centimeters. Its area is n square centimeters, where n is a prime number. What is the greatest possible value of n?

(A) 11

(B) 12

(C) 19

(D) 23

(E) 24

Answer Key 2: Triangles

Concept Review 2

1. 360°

2. 1,080°

3. Draw a diagram. If the measure of ∠A is 65° and the measure of ∠B is 60°, then the measure of ∠C must be 55°, because the angles must have a sum of 180°. Since ∠A is the largest angle, the side opposite it, , must be the longest side.

4. 60°. Since all the sides are equal, all the angles are, too.

5. No, because an isosceles triangle must have two equal angles, and the sum of all three must be 180°. Since , and , the triangle is impossible.

6. Your diagram should look something like this:

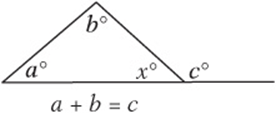
7. If a triangle has sides of lengths 20 and 15, then the third side must be less than 35 (their sum) but greater than 5 (their difference).

8. No. The sum of the two shorter sides of a triangle is always greater than the third side, but is not greater than 14. So the triangle is impossible.

9. 25° and 130° or 77.5° and 77.5°

10. Draw in the line segments PQ, PR, PS, and PT. Notice that this forms two triangles, ΔPQS and ΔPRT. Since any two sides of a triangle must have a sum greater than the third side, , and Therefore, .

SAT Practice 2

1. A If , then, by the Isosceles Triangle theorem, ∠BAD and ∠BDA must be equal. To find their measure, subtract 50° from 180° and divide by 2. This gives 65°. Mark up the diagram with this information. Since the angles in the big triangle have a sum of 180°, , so .

2. 500 Drawing two diagonals shows that the figure can be divided into three triangles. (Remember that an n-sided figure can be divided into n – 2 triangles.) Therefore, the sum of all the angles is . Subtracting 40° leaves 500°.

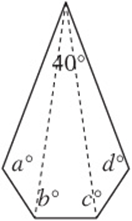
3. B The third side of any triangle must have a length that is between the sum and the difference of the other two sides. Since and , the third side must be between (but not including) 7 and 25.

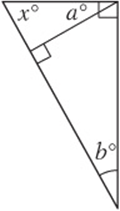
4. A Since the big triangle is a right triangle, must equal 90. The two small triangles are also right triangles, so is also 90. Therefore, and statement I is true. In one “solution” of this triangle, a and b are 65 and x is 25. (Put the values into the diagram and check that everything “fits.”) This solution proves that statements II and III are not necessarily true.

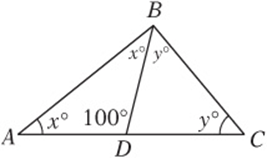
5. C If , then, by the Isosceles Triangle theorem, the angles opposite those sides must be equal. You should mark the other angle with an x also, as shown here. Similarly, if then the angles opposite those sides must be equal also, and they should both be marked y. Now consider the big triangle. Since its angles must have a sum of 180, . Dividing both sides by 2 gives . (Notice that the fact that ADB measures 100° doesn”t make any difference!)

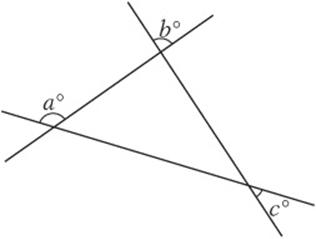
6. E Label the two angles that are “vertical” to those marked b and c. Notice that the angle marked a is an “external” angle. By the External Angle theorem, .

7. D Write in the missing angle measures by using the fact that the sum of angles in a triangle is 180°. Then use the fact that the biggest side of a triangle is always across from the biggest angle to order the sides of each triangle.

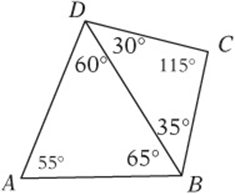
8. A Consider the side of length 4 to be the base, and “attach” the side of length 6. Notice that the triangle has the greatest possible height when the two sides form a right angle. Therefore, the greatest possible area of such a triangle is , and the minimum possible area is 0. The greatest prime number less than 12 is 11.