SAT Test Prep

CHAPTER 10
ESSENTIAL GEOMETRY SKILLS

Lesson 5: Areas and Perimeters

The Formulas

The only area or perimeter formulas you will need for the SAT will be given at the beginning of each section:

Reference Information

The arc of a circle measures 360°.

Every straight angle measures 180°.

The sum of the measures of the angles in a triangle is 180°.

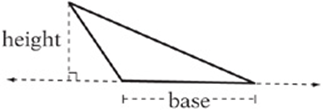
Finding the area of an obtuse triangle can be tricky. Keep in mind that any side can be the base—rotate the triangle if it helps. Also remember that an altitude might be outside the triangle, as in the diagram below.

Don”t confuse the area formula for a circle (πr²) with the circumference formula (2πr). Just remember that areas are measured in square units, so the area formula is the one with the radius squared.

Using Diagrams

If a geometry problem doesn”t include a figure, draw one, because seeing the relationships among the parts is essential to solving geometry problems! If it does include a figure, mark it up with any information you find!

You can use the diagram to estimate angle measures and lengths, unless it is labeled “Note: Figure not drawn to scale,” which means that the figure is drawn inaccurately, or in only one of many different possible ways. In this case, it often helps to redraw the figure. If it”s drawn inaccurately, redraw it accurately, and see whether anything important changes. If it can be drawn in different ways, redraw it so that it is as different as possible from the original, but all of the given information is maintained.

Strange Shapes

Don”t panic when you see a strange-looking shape on an SAT. Just notice how the shape relates to simple shapes.

Example:

In the figure below, the shaded region is constructed of only horizontal and vertical sides. That is, all angles are right angles. What is the perimeter of the shaded region?

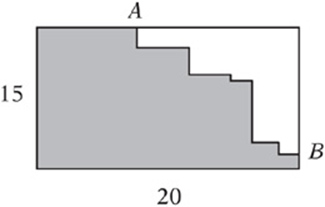
Compare the shaded region to the rectangle, but keep in mind that the question asks about the perimeter, not the area! Even though the area of the shaded region is clearly less than the area of the rectangle, their perimeters must be the same! How do we know? Consider the two different paths from A to B. Notice that all the horizontal segments of the “jagged” path add up in length to the horizontal part of the “simple” path along the rectangle. The same is true of the vertical parts. So the perimeter is .

Example:

If the circle with center C has an area of 16, what is the area of the shaded region?

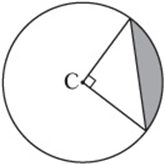
Piece together the strange shape from simple shapes. Notice that the shaded region is simply a quarter of the circle minus the triangle. If the area of the circle is 16π, then a quarter of the circle has an area of 4π. Since , the radius must be 4. Therefore, the base and height of the triangle are both 4, and the area of the triangle is . Therefore, the area of the shaded region is .

Concept Review 5: Areas and Perimeters

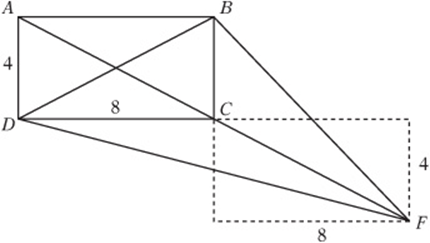
Draw a diagram in the space below for the following situation: The length and width of rectangle ABCD are integers. The area of ABCD is 32. Diagonal AC is extended to point F such that C is the midpoint of AF.

1. If the area of ABCD is 32, what is the area of ΔFDB?

2. What is the ratio of the area of ΔFCB to the area of ΔFAD?

Questions 3 and 4 pertain to the diagram below, in which P is the center of the semicircle.

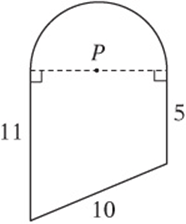
3. What is the area of the figure above?

4. What is the perimeter of the figure above?

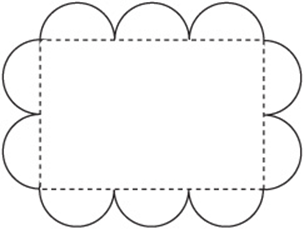
5. The figure above consists of a rectangle and a curved path which is made up of 10 semicircles of equal diameter. If the total length of this curved path is 40π, then the area of the rectangle is

(A) 40

(B) 80

(C) 96

(D) 192

(E) 384

SAT Practice 5: Areas and Perimeters

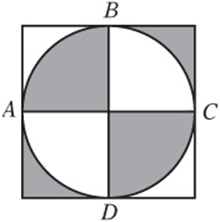
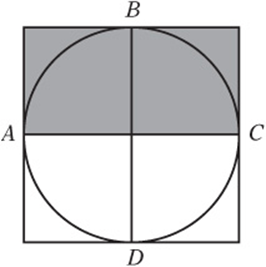
1. In the figure above, a circle is inscribed in a square and intersects the square at points A, B, C, and D. If , what is the total area of the shaded regions?

(A) 18

(B) 36

(C) 18π

(D) 24π

(E) 72

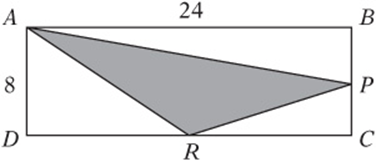
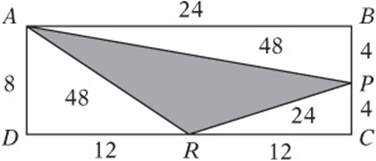
2. In the figure above, ABCD is a rectangle and P and R are midpoints of their respective sides. What is the area of ΔAPR?

(A) 54

(B) 68

(C) 72

(D) 78

(E) 96

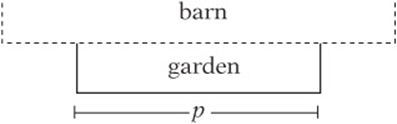
3. A fence encloses three sides of a rectangular garden that is bordered on the other side by a barn, as shown in the figure above. If the total length of the fence is 44 meters and p is the length, in meters, of the fence parallel to the barn wall, then which of the following expresses the area of the garden?

(C) 22p

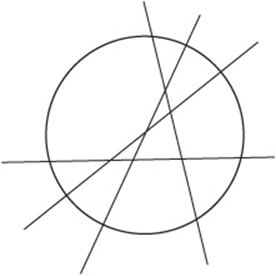
4. What is the maximum number of pieces that can be cut from a paper circle with four straight cuts if none of the pieces are moved or folded between cuts?

(A) 7

(B) 8

(C) 9

(D) 10

(E) 11

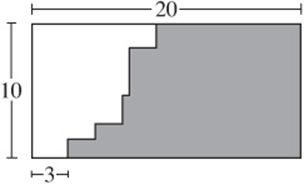
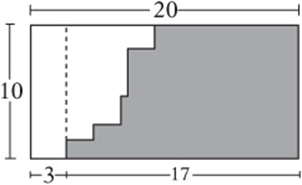
5. In the figure above, all angles shown are right angles. What is the perimeter of the shaded region?

(A) 51

(B) 54

(C) 57

(D) 60

(E) 63

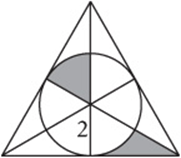
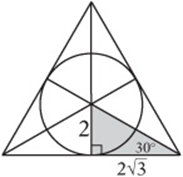
6. The figure above consists of a circle with radius 2 inscribed in an equilateral triangle in which all three interior angle bisectors are drawn. What is the total area of the shaded regions?

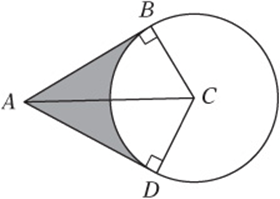
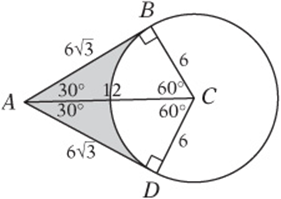
7. In the figure above, C is the center of the circle, , and . What is the perimeter of the shaded region?

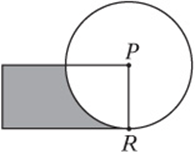
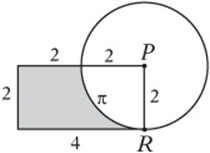
8. In the figure above, PR is the radius of the circle as well as a side of the rectangle. If the circle has an area of 4π and the rectangle has an area of 8, then what is the perimeter of the shaded region?

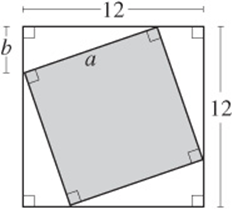
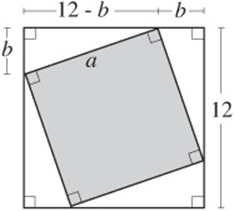
9. The figure above shows a square with sides of 12 centimeters in which a smaller square with sides a centimeters is inscribed. If a is an integer and , then what is one possible value for the area of the shaded square?

Answer Key 5: Areas and Perimeters

Concept Review 5

Your diagram should look something like the one above, although the rectangle can also have dimensions of 1 and 32 or 2 and 16.

1. Think of the area of ΔFDB as the sum of the areas of ΔDCB, ΔFDC, and ΔFCB. Each of these triangles has an area that is half of the rectangle, because each one has the same base and height as the rectangle. (If you have a tough time seeing this, think of BC as the base of ΔFCB and CDas the base of ΔFDC. Since these triangles are obtuse, their heights are “outside” the triangles.) Therefore, the area of ΔFDB is .

2. We just found that ΔFCB has an area of 16. The area of ΔFAD is the area of ΔFCD = the area of ΔADC, which is . Therefore, the ratio is 1:2.

3. Draw the extra segment as shown and determine its length from the Pythagorean theorem. (It”s a 3-4-5 right triangle times 2!) The area of the semicircle is , the area of the rectangle is 40, and the area of the triangle is 24, for a total area of .

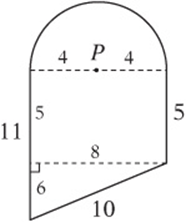
4. The perimeter of the semicircle is 4π, so the perimeter of the whole figure is .

5. E Each semicircle has a perimeter of 4π, which means the circumference of a “whole” circle would be 8π and therefore the diameter of each circle is 8. Therefore, the height of the rectangle is 16 and the length is

SAT Practice 5

1. E Move the shaded pieces around to see that they make up half of the square. The area of the square is , so the shaded region has area .

2. C Find the area indirectly by subtracting the three right triangles from the rectangle. The rectangle has area , so the triangle has area .

3. B The length of the garden is p. The width is half of 44 -p. Therefore, the area is .

4. E You get the maximum number of pieces (11) by making sure that each cut intersects every other previous cut in a new spot. Your diagram should look something like this, with six points of intersection in the circle.

5. B Draw the extra line shown here to see that the shaded region has a perimeter equal to a 10-by-17 rectangle. Therefore its perimeter is .

6. A Move the pieces together to see that they form a right triangle. Since all of the interior angles of an equilateral triangle are 60° and the bisectors divide them in half, the triangle is a 30°-60°-90° triangle, so its base must be and , and the area is .

7. E The two right triangles have two pairs of equal sides (the two radii and the shared hypotenuse), so they must be congruent triangles. Arc BD is¹/3 of the circle, with circumference 12π. Therefore, you should be able to determine the measures shown in this diagram and see that the perimeter of the shaded region is .

8. A If the circle has an area of 4π, its radius is 2. If the rectangle has an area of 8, its length must be 4. The arc portion of the shaded region is¹/4 of the circle with circumference 4π, so the perimeter is .

9. 81 or 100 Consider the right triangle in the upper-left corner of the diagram. Notice that it has a hypotenuse of a and legs of length b and . The question is asking for the area of the shaded square, which is a². By the Pythagorean theorem, . Since , the maximum possible value of , and the minimum possible value of . Since a must be an integer, a² must be a perfect square, and the only perfect squares between 74 and 104 are 81 and 100.