The SAT Prep Black Book
SAT Math
SAT Math Toolbox
In a moment, we”ll talk about how to attack the SAT Math section from a strategic perspective. But first, it”s important to make sure we know all the mathematical concepts the SAT is allowed to test (don”t worry, there aren”t that many of them).
If you already know all the concepts below, then you don”t need to go over them again. Instead, go to the next section and start learning how to attack the test.
If you”re not familiar with some of the concepts below, then take a few minutes to refresh yourself on them.
This concept review is designed to be as quick and painless as possible. If you feel that you”d like a little more of an explanation, the best thing to do is find somebody who”s good at math (a teacher, parent, or friend) and ask them to spend a little time explaining a few things to you.
This concept review might seem easier to you than the actual SAT Math section. That”s because the difficulty in SAT Math really comes from the setup of each problem, not from the concepts that the problem involves. The concepts in this review are the same concepts you”ll encounter in your practice and on the real test, but the real test often makes questions look harder than they really are by combining and disguising the underlying concepts in the questions.
For SAT Math, it”s not that important to have a thorough understanding of the underlying concepts. All you need is a quick, general familiarity with a few basic ideas. So that”s all we”ll spend time on.
Please note that this list is similar in some ways to chapters 14 through 18 of the College Board publication The Official SAT Study Guide, but my list is organized a little differently and presents the material in more discrete units. In addition, my list explains things in plainer language and omits some concepts that are redundant, making it easier to study.
As you”re going through this list, you may see concepts that aren”t familiar. Before you let yourself get confused, make sure you”ve read this list through TWICE. You”ll probably find that a lot of your confusion clears itself up on the second reading.
Also, please try to remember that the material in the Math Toolbox is pretty dry and technical, and that it”s not the focus of the proper strategic approach to the SAT. It”s just a set of basic ideas that need to be refreshed before we get into the more important stuff.
Properties of integers
An integer is any number that can be expressed without a fraction, decimal, percentage sign, or symbol.
Integers can be negative or positive.
Zero is an integer.
Example:
These numbers are integers: -99, -6, 0, 8, 675
These numbers are NOT integers: pi, 96.7, 3/4
There are even integers and there are odd integers.
Only integers can be odd or even—a fraction or symbolic number is neither odd nor even.
Integers that are even can be divided by 2 without having anything left over.
Integers that are odd have a remainder of 1 when they”re divided by 2.
Example:
These are even integers: -6, 4, 8
These are odd integers: -99, 25, 675
An even number plus an even number gives an even result.
An odd number plus an odd number gives an even result.
An odd number plus an even number gives an odd result.
An even number times an even number gives an even result.
An even number times an odd number gives an even result.
An odd number times an odd number gives an odd result.
Some integers have special properties when it comes to addition and multiplication:
Multiplying any number by 1 leaves the number unchanged.
Dividing any number by 1 leaves the number unchanged.
Multiplying any number by 0 results in the number 0.
Adding 0 to any number leaves the number unchanged.
Subtracting 0 from any number leaves the number unchanged.
It”s impossible, for purposes of SAT Math, to divide any number by 0.
Word problems
SAT word problems are typically simple descriptions of one of the following:
Real-life situations
Abstract concepts
Example:
An SAT word problem about a real-life situation might look like this:
“Joe buys two balloons for three dollars each, and a certain amount of candy. Each piece of the candy costs twenty-five cents. Joe gives the cashier ten dollars and receives twenty-five cents in change. How many pieces of candy did he buy?”
An SAT word problem about an abstract concept might look like this:
“If x is the arithmetic mean of seven consecutive numbers, what is the median of those seven numbers?”
To solve SAT word problems, we have to transform them into math problems. These are the steps we follow to make that transformation:
Note all the numbers given in the problem, and write them down on scratch paper.
Identify key phrases and translate them into mathematical symbols for operations and variables. Use these to connect the numbers you wrote down.
Example:
In the phrase “two balloons for three dollars each,” the each part means we have to multiply the two balloons by the three dollars in order to find out how much total money was spent on the two balloons. 2 * 3 = 6. Six dollars were spent on the two balloons if they cost three dollars each.
After the word problem has been translated into numbers and symbols, solve it like any other SAT Math problem (see the SAT Math Path in this chapter for more on that).
Number lines
A number line is a simple diagram that arranges numbers from least to greatest.
The positions on a number line can be labeled with actual numbers or with variables.
Example:
This number line shows all the integers from -7 to 4:

On the SAT, number lines are drawn to scale and the tick marks are spaced evenly unless the question notes otherwise.
To determine the distance between two numbers on a number line, just subtract the number to the left from the number to the right.
Example:
On the number line above, the distance between 1 and 3 is two units, which is the same thing as saying that 3 – 1 = 2.
On a number line, there is a DIFFERENCE between the distance that separates two numbers and the number of positions between them.
If you”re asked how many positions are BETWEEN two numbers on a number line, remember that you CANNOT answer this question by simply subtracting one number from the other—that”s how you would find the distance. You should actually count the positions—you”ll find the number of positions is one less than the difference you get when you subtract.
Example:
On the number line above, there are NOT two positions between the numbers 2 and 4, even though 4 – 2 = 2. There is only one position between the numbers 2 and 4, which is one less than the difference we get when we subtract the number 2 from the number 4.
On the SAT, the positions on a number line don”t have to represent whole numbers. They might represent groups of five numbers at a time, or hundredths, or any other consistent amount.
A number”s absolute value is the distance of that number from zero on the number line.
Example:
-4 and 4 both have an absolute value of 4. We signify the absolute value of a number with vertical lines on either side of the number:
|-4| = |4| = 4.
Squares and square roots
To square a number, multiply the number by itself.
Example:
Five squared is five times five, or 5 * 5, or 25.
To find the square root of a number, find the amount that has to be multiplied by itself in order to generate the number.
Example:
The square root of 25 is the amount that yields 25 when it”s multiplied by itself. As we just saw, that amount is 5. So the square root of 25 is 5.
When you square any number, the result is always positive. This is because a positive number times a positive number gives a positive result, and so does a negative number times a negative number.
Square roots on the SAT are always positive.
The SAT never asks about the square root of a negative number.
The SAT likes to ask about the squares of the numbers -12 through 12. Here they are:
Number Square
-12 or 12 144
-11 or 11 121
-10 or 10 100
-9 or 9 81
-8 or 8 64
-7 or 7 49
-6 or 6 36
-5 or 5 25
-4 or 4 16
-3 or 3 9
-2 or 2 4
-1 or 1 1
0 0
While I don”t recommend using a calculator on the SAT if you can help it, remember that you can always find the square root of a number very easily on a good calculator.
Fractions and rational numbers
A fraction is a special type of number that represents parts of a whole.
Fractions are written this way:
[number of parts being described in the situation]
[number of parts that the whole is divided into]
Example:
Imagine that we”re sharing a six-pack of soda cans. I really like soda, so I drink five of the cans. In this situation, I”ve had five of the six cans that make up the six-pack—I”ve had 5/6 of the six-pack.
The number above the fraction bar is called a numerator.
The number under the fraction bar is called a denominator.
When the numerator of a fraction is less than the denominator, the value of the fraction is less than 1.
When the numerator of a fraction is greater than the denominator, the value of the fraction is greater than 1.
Example:
1/2 is equal to one half, which is less than 1. 6/3 is equal to 2, which is greater than 1.
Any integer can be thought of as having the denominator 1 already underneath it.
Example:
7 is the same thing as 7/1.
A reciprocal is what you get if you switch the numerator and the denominator of a fraction.
Example:
The reciprocal of 2/3 is 3/2. The reciprocal of 7 is 1/7. (Remember that all integers can be thought of as having the denominator 1.)
To multiply two fractions, first multiply their numerators and write that amount as the numerator of the new fraction; then, multiply the denominators and write that amount as the denominator of the new fraction.
Example:
4/7 x 9/13 = 36/91
To divide fraction a by fraction b, we actually multiply fraction a by the RECIPROCAL of fraction b.
Example
4/7 divided by 9/13 = 4/7 x 13/9 = 52/63
Multiplying a non-zero integer by a fraction that”s less than 1 (that is, by a fraction where the numerator is less than the denominator) will give a result that is closer to zero on a number line than the original integer was. (Read this item again if you need to!)
Examples:
6 x 3/5 = 18/5, and 18/5 falls between 0 and 6 on a number line.
-7 x 2/9 = -14/9, and -14/9 falls between -7 and 0 on a number line.
Fraction a is equal to fraction b if you could multiply the numerator in a by a certain number to get the numerator in b, and you could also multiply the denominator in a by the same number to get the denominator of b.
Example:
3/5 is equal to 18/30 because 3 x 6 = 18 and 5 x 6 = 30. Here”s another way to write this: 3/5 x 6/6 = 18/30. Notice that 6/6 is the same thing as 1 (six parts of a whole that”s divided into six parts is the same thing as the whole itself). So all we really did here was multiply 3/5 by 1, and we know that doing this will give us an amount equal to 3/5.
For more on fractions, see the discussion of factors and multiples below.
Factors
The factors of a number x are the positive integers that can be multiplied by each other to achieve that number x.
Example:
The number 10 has the factors 5 and 2, because 5 * 2 = 10. It also has the factors 10 and 1, because 1 * 10 = 10.
“Common factors,” as the name suggests, are factors that two numbers have in common.
Example:
The number 10 has the factors 1, 2, 5, and 10, as we just saw. The number 28 has the factors 1, 2, 4, 7, 14, and 28. So the common factors of 10 and 28 are 1 and 2, because both 1 and 2 can be multiplied by positive integers to get both 10 and 28.
Multiples
The multiples of a number x are the numbers you get when you multiply x by 1, 2, 3, 4, 5, and so on.
Example:
The multiples of 4 are 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, and so on.
Remainders
Remainders are what you get when you divide one number by another number and have something left over (this assumes you don”t use fractions or decimals to write the answer to your division problem).
Example:
If we divide 30 by 4, we see that it doesn”t work out evenly. 4 * 7 = 28, which isn”t enough, and 4 * 8 = 32, which is too much. So if we divide 30 by 4, one way to state the answer is to say that 30 divided by 4 is “7 with a remainder of 2,” because 4 * 7 = 28 and
28 + 2 = 30.
The remainder in a division problem must be less than the number we”re dividing by.
Example:
It doesn”t make any sense to say that 30 divided by 4 is “3 with a remainder of 18,” because 18 is bigger than 4 and 4 will still go into 18 a few more times.
As a reminder, when you first learned to divide, you were probably taught to use remainders.
Most calculators don”t give remainders when solving division problems—instead, they give fractions or decimals.
Prime numbers
A prime number is a number that has exactly two factors: 1 and itself.
Example:
17 is a prime number because there are no positive integers besides 1 and 17 that can be multiplied by other integers to generate 17. (Try to come up with some—you won”t be able to.)
24 is NOT a prime number because there are a lot of positive integers besides 1 and 24 that can be multiplied by other integers to generate 24. For example, 2, 3, 4, 6, 8, and 12 can all be multiplied by other integers to generate 24.
All prime numbers are positive.
The only even prime number is 2.
1 is NOT a prime number because it has only one factor (itself), while prime numbers must have exactly two factors.
Ratios, proportions, and percentages
Ratios, proportions, and percentages are all ways to express a relationship between two numbers.
A ratio is written as a pair of numbers with a colon between them.
Example:
If you make 5 dollars for every 1 dollar Bob makes, then the ratio of your pay to Bob”s pay is 5 : 1.
A proportion is usually written as a fraction, with a number in the numerator compared to the number in the denominator.
Example:
If you make 5 dollars for every 1 dollar Bob makes, then your pay can be compared to Bob”s pay with the proportion 5/1. (Or, if we wanted to compare what Bob makes to what you make, that proportion would be 1/5.)
A percentage is a special proportion where one number is compared to 100.
To determine a percentage, first compare two numbers with a proportion, and then divide the top number by the bottom number and multiply the result by 100.
Example:
If Bob makes 1 dollar for every 5 dollars you make, then the proportion that compares Bob”s pay to your pay is 1/5. If we divide 1 by 5 and multiply by 100, we see that Bob makes 20% of what you make.
Ratios can be set equal to each other and “cross-multiplied.” (If you don”t already know how to do this, don”t worry—it”s just a short cut around regular algebraic techniques. You don”t have to know how to do it for the SAT.)
If the relationship between two quantities is the kind where increasing one quantity results in an increase in the other quantity, then we say those two quantities “vary directly” or are “directly proportional.”
Example:
If I make 1 dollar for every 5 dollars you make, then when I make 4 dollars you make 20 dollars—increasing my pay to 4 leads to an increase in your pay to 20. That means our two rates of pay are in direct proportion.
If two quantities are related so that increasing one decreases the other, then we say those two quantities “vary indirectly” or are “inversely proportional.”
Example:
If we have two quantities x and y set up so that xy = 20, then x and y are inversely proportional—every time one increases, the other one decreases, and vice-versa. So if x starts out as 10 and y starts out as 2, changing x to 5 means we have to change y to 4—as one decreases, the other increases.
Sequences
Sequences are strings of numbers that follow a rule, so that knowing one number in the sequence allows us to figure out another number in the sequence.
Sequence questions on the SAT will rarely operate in exactly the same way that a question about an arithmetic or geometric series would work in a math class, though the College Board often tries to mislead you by making a sequence question look deceptively similar to a traditional question about a series.
SAT sequences can either go on forever or stop at some point, depending on the setup of the question.
There are two common types of SAT sequences, and we can classify them by the rules that are used to figure out which numbers go in the sequence. Let”s look at the different types of SAT sequences:
Example:
The sequence 3, 5, 7, 9, 11, 13, . . . follows a very simple rule: to get the next number in the sequence, just add 2 to the number before. So the next number in this sequence would be 15, then 17, and so on.
The sequence 3, 15, 75, 375, . . . also follows a simple rule: to get the next number, multiply the previous number by 5. The next number here would be 1,875.
The Math section MIGHT ask you to figure out:
oThe sum of certain terms in a sequence.
oThe average of certain terms.
oThe value of a specific term.
If you studied sequences in school, they were probably a lot harder in your math class than they will be on the SAT. For example, there”s no sigma notation on the SAT. (If you”ve never heard of sigma notation, don”t worry about it.)
Set theory
Sets are collections of things.
Sets on the SAT are usually groups of numbers.
Example:
The set of factors of 24 is {1, 2, 3, 4, 6, 8, 12, 24}.
On the SAT, the things in a set can be called “members” of that set or “elements” of that set.
The “union” of two or more sets is what we get when we combine all of the members of those sets into a bigger set.
Example:
The set of factors of 24 is {1, 2, 3, 4, 6, 8, 12, 24} and the set of factors of 36 is {1, 2, 3, 4, 6, 9, 12, 18, 36}. That means the union of those two sets is the set {1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36}.
The “intersection” of two or more sets is the set of members that the two sets have in common.
Example:
Given the sets {1, 2, 3, 4, 6, 8, 12, 24} and {1, 2, 3, 4, 6, 9, 12, 18, 36}, the “intersection” is {1, 2, 4, 6, 12}, because those members are common to both sets.
Counting problems
On the SAT, “counting problems” are problems where you”re asked to give the total number of ways that two or more events might happen.
If you”ve studied these types of problems in math class, you probably called them “permutation and combination” problems.
The general, basic rule of these types of problems is this: when you have two events, and the first event might happen in any one of x ways, and the second event might happen in any one of y ways, then the total number of ways that both events could happen together is given by xy. (That might sound a little complicated—let”s do an example.)
Example:
Imagine there are three roads between your house and your friend”s house, and there are 6 roads between your friend”s house and the library. If you”re driving from your house to your friend”s house and then to the library, how many different ways can you go?
There are 3 ways to get from your house to your friend”s house. So the event of you getting to your friend”s house can happen in any one of 3 ways. Then there are 6 ways to get from your friend”s house to the library, so the event of going to the library from the friend”s house can happen in any one of 6 ways. This means the total number of paths you could travel from your house to your friend”s house and then on to the library is given by 3 * 6, which is 18.
The key to solving these types of problems is making sure you correctly count the number of possible outcomes for each event.
Example:
Imagine that there are 3 roads between your house and your friend”s house. You”re going to visit her and then return home. For some reason, you can”t travel the same road twice.What”s the total number of ways you could go from your house to your friend”s house and back?
Well, the total number of ways to go from your house to your friend”s house is 3, and the total number of ways to come back home is ONLY 2. Why can you only come back from your friend”s house in 2 ways? Because the problem says you”re not allowed to use the same road twice, and when you go back home you will already have used one of the three roads to visit your friend in the first place. So the right way to answer this is to multiply 3 * 2, NOT 3 * 3. That means the answer is 6, NOT 9.
Operations on algebraic expressions
Algebraic expressions are figures that include variables.
Algebraic expressions, just like the regular numbers they represent, can be added, subtracted, multiplied, and divided—but sometimes there are special rules that apply.
We can add or subtract two algebraic expressions when they involve the same variable expressions.
Example:
We can add 5x and 19x to get 24x, because the 5x and 19x both involve the same variable expression: x. We can subtract 17xyz2 from
100 xyz2 and get 83xyz2 because they both involve the variable expression xyz2.
But if we want to add 5x to 17 xyz2, we can”t combine those two expressions any further because they have different variable expressions. So we would just write “5x + 17xyz2” and leave it at that.
We can multiply any two algebraic expressions by multiplying all the terms in the first expression by all the terms in the second expression.
Example:
5x * 7y = 35xy
(5a + 2)(4b + 9) = 20ab + 45a + 8b + 18
We can divide any algebraic expression by another algebraic expression when they share factors. (See the discussion on factoring algebraic expressions.)
Example:
26xy/13x = 2y
When multiplying two algebraic expressions on the SAT, we can often use the “FOIL” technique. “FOIL” stands for “First, Outer, Inner, Last,” and refers to the order in which the terms of the two expressions are multiplied by one another.
You have probably used FOIL in your math classes, but if you used some other technique there”s no need to worry.
Example:
To multiply the expressions (5x + 7) and
(3x + 4), we can use FOIL.
The “First” pair in the acronym is the 5x and the 3x, because they are the first terms in each expression. We multiply these and get 15x2.
The “Outer” pair in the acronym is the 5x and the 4. We multiply these and get 20x.
The “Inner” pair in the acronym is the 7 and the 3x. We multiply these and get 21x.
The “Last” pair in the acronym is the 7 and the 4. We multiply these and get 28.
Now we just add up all those terms and we get the expression 15x2 + 20x + 21x + 28, which we can simplify a little bit by combining the two like x terms, giving us:
15x2 + 41x + 28
So (5x + 7)(3x + 4) = 15x2 + 41x + 28
If this seems a little complicated now, don”t worry about it. You”ll get it with practice—and there isn”t that much of it on the SAT anyway.
Factoring algebraic expressions
On the SAT, factoring an algebraic expression involves breaking the expression down into two other expressions that could be multiplied by each other to give the original expression.
Example:
If we have an algebraic expression like (8x + 4), we can break that down into the factors 4 and (2x + 1), because 4(2x + 1) = 8x + 4.
On the SAT, there are three types of factoring situations you”ll need to recognize:
orecognizing common factors
odoing “FOIL” in reverse
orecognizing a difference of squares
Recognizing common factors involves noticing that every term in a given expression has a common factor, as we did in the last example.
Example:
In the expression (21xy + 7x), both of the terms in the expression have a common factor of 7x, so we can factor the expression like this: 7x(3y + 1).
Factoring polynomials basically involves doing the “FOIL” process in reverse. Trust me, it”s not as hard as it looks. It just takes a little practice.
Example:
9x2 – 21x + 12 = (3x – 3)(3x – 4)
5x2 – 3x – 2 = (5x + 2)(x – 1)
When we factor the difference of two squares, there”s a shortcut we can use—the difference of two squares can be factored as the product of the sum of the square roots of the two squares times the difference of the square roots of the two squares. Let”s see an example.
Example:
9x2 – 4 = (3x + 2)(3x – 2)
Exponents
An exponent of a number is what we get when we multiply the number by itself a certain number of times.
Example:
x * x * x = x3 is an example of an exponential expression. The 3 in this example is the exponent, and the x is called the “base.”
Exponents can be positive or negative.
When an exponent is positive, we multiply the base by itself as many times as the exponent indicates, just like we did in the above example.
When an exponent is negative, we treat it just like a positive exponent EXCEPT that we take the reciprocal of the final amount (take another look at the discussion of reciprocals on page).
Example:
x5 = x * x * x * x * x
x -5 = 1/(x5)
We can multiply exponent expressions by each other when the bases are identical. To do that, we just add the exponents:
Example:
(x6)(x4) = (x * x * x * x * x * x) (x * x * x * x) =
x * x * x* x * x * x * x * x * x * x = x10
(x7)(x - 4) = x3
We can also divide exponent expressions when they have the same base. For that we just subtract the exponents:
Example:
(x8)/(x2) = x6
Finally, we can raise exponential expressions to other exponents by multiplying the first exponent by the second one:
Example:
(x4)5 = x20
Note that raising any number to an exponent of zero gives you the number 1.
Example:
y0 = 1
Using equations
On the SAT, an equation is a statement that involves an algebraic expression and an equals sign.
Example:
5x = 20 is an equation, because it involves the algebraic expression 5x and an equals sign.
Solving an equation means figuring out how much the variable in the equation is worth. We can solve equations just like you learned in algebra class—by multiply, dividing, adding, or subtracting both sides of the equation by the same amounts until we”re left with a value for the variable.
Example:
5x = 20
5x/5 = 20/5
x = 4
On the SAT, we can often use equations to answer a question even when we can”t solve the equation for each variable individually.
Example:
We might be told that (a + b)/10 = 15. How can we figure out the value of a + b? In school, you might try to figure out a first, and then b, and then add them together. But we don”t have enough information to do that. So what can we do? Well, we just solve for the entire amount a + b. In this situation, we can do that by multiplying both sides by 10, so a + b = 150. In this case, even though we can never know the individual values of a and b, we can know the sum a + b.
On the SAT, we can also solve equations “in terms of” one particular variable. To do this, we just isolate the target variable on one side of the equation.
Example:
What if we have to solve this expression in terms of n?
4n + 7y = 2a
4n = 2a – 7y
n = (2a – 7y)/4
n = (2a – 7y)/4
Sometimes you”ll have a “system” of equations. A system of equations contains two or more equations with the same variables.
Example:
This is a system of equations:
x + y = 5
2x – y = 7
The easiest way to solve a system of equations is to solve one equation in terms of one variable, like we just did before. Then we substitute in the second equation and solve.
Example:
First, we”ll isolate the y in the first equation, giving us that equation in terms of y: y = 5 – x. Now that we know y is the same thing as 5 – x, we just plug in 5 – x where y appears in the second equation:
2x – (5 – x) = 7
2x – 5 + x = 7
3x – 5 = 7
3x = 12
x = 4
Now that we know x is 4, we just plug that back into the first equation, and we”ll be able to solve for y:
4 + y = 5
y = 1
Inequalities
On the SAT, inequalities are statements that show a particular amount may be greater than or less than a second amount. They use these symbols:
The symbol < means “less than.”
The symbol > means “greater than.”
The symbol < means “less than or equal to.”
The symbol > means “greater than or equal to.”
You solve an inequality the same way you solve an equation, with one difference: when you multiply by -1 to solve for a variable, you have to switch the direction of the inequality symbol.
Example:
-x/4 = 10 -x/4 < 10
-x = 10(4) -x < 10(4)
-x = 40 -x < 40
x = -40 x > -40
Solving quadratic equations by factoring
A quadratic equation is an equation that involves three terms:
oone term is a variable expression raised to the power of 2.
oone term is a variable expression not raised to any power.
oone term is a regular number with no variable.
Example:
x2 + 3x = -2 is a quadratic equation because it involves a term with x squared, a term with x, and a regular number.
There is only one way to solve quadratic equations on the SAT, and that is by factoring. (See the discussion of factoring above).
To solve a quadratic equation by factoring, we have to make one side of the equation equal to zero, and then factor the other side of the equation (the quadratic part).
Example:
x2 +3x = -2
x2 +3x + 2 = 0
(x + 1)(x + 2) = 0
Now that we know (x + 1)(x + 2) = 0, what else do we know? We know that one of those two factors has to equal zero—either x + 1 = 0 or x + 2 = 0. How do we know this? Remember that the only way to multiply two numbers and get zero is if one of the numbers is zero. So if we can multiply x + 1 by x + 2 and get zero, then either x + 1 is zero or x + 2 is zero.
Once we”ve factored, we solve for the variable by creating two small sub-equations in which each factor is set equal to zero.
x + 1 = 0 or x + 2 = 0
x = -1 or x = -2
So in the equation x2 + 3x = -2 , x can equal either -1 or -2.
Quadratic equations can have multiple solutions, as we”ve just seen.
Functions
Functions are formulas that tell you how to generate one number by using another number.
Functions can be written in a lot of ways. On the SAT, they”ll usually be written in f(x) notation, also called “function notation.”
Example:
f(x) = x3 + 4 is a function written in function notation.
When we write with function notation, we don”t have to use f(x) specifically. We could write g(n), a(b), or whatever.
Don”t confuse function notation like f(x) with the multiplicative expression (f)(x), which means “f times x”!
When we evaluate a function for a certain number x, it means that we plug the number x into the function and see what the f(x) is.
Example:
If our function is f(x) = x3 + 4 and we want to evaluate the function where x = 2, then we get this:
f(x) = x3 + 4
f(2) = (2)3 + 4
f(2) = 8 + 4
f(2) = 12
So for our function, when x equals 2, the f(x) equals 12.
The “domain” of a function is the set of numbers on a number line where the function can be evaluated.
Example:
In the function f(x) = x3 + 4, the domain is all the numbers on the number line, because we can put any value from the number line in for x and get a result for f(x).
In the function f(x) = √x, the domain is only those numbers that can have a square root. Remember that, on the SAT, you can”t take the square root of a negative number. That means the domain for the function f(x) = √x is the set of non-negative numbers.
The “range” of a function is the set of numbers that f(x) can come out equal to.
Example:
The function f(x) = x3 + 4 has a range of negative infinity to positive infinity—by putting in the right thing for x, we can get any number we want as f(x).
The function f(x) = √x has a range of only non-negative numbers, because there is no way to put any number as x and get a number for f(x) that”s negative.
Linear functions
A point can be plotted on a graph in (x, y) notation if we take the x number and make it the horizontal separation between the point (x, y) and the origin (0, 0), and then we make the y value the vertical separation between (x, y) and (0, 0).
A linear function is a function in which the f(x) is replaced with a y, and all the (x, y) pairings form a straight line when they”re plotted on a graph.
Example:
The function f(x) = (x/2) + 1 is linear, because all of the (x, y) pairings that it generates fall in a straight line when they”re plotted as lines on a graph.
Here”s a chart that shows some (x, y) pairings for the function f(x) = (x/2) + 1:
x y
0 1
1 1.5
2 2
3 2.5
4 3
5 3.5
6 4
7 4.5
8 5
9 5.5
10 6
11 6.5
12 7
13 7.5
14 8
15 8.5
16 9
When we plot these points on a graph, we see that they fall in a straight line:
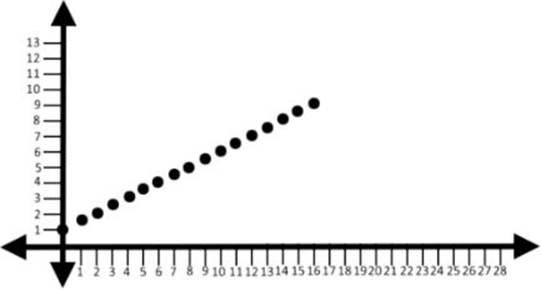
Of course, the points plotted on the graph are only the (x, y) pairings when x is a positive integer. But isn”t the domain for f(x) = (x/2) + 1 all the numbers on the number line? That means that there must be an f(x) even where x equals 1.135623, or 8.4453, or any other number at all. For every value on the x axis, there”s a corresponding f(x) value on the y axis. We could “connect the dots” on our graph above, and extend the line of our function infinitely in either direction. Let”s do that:
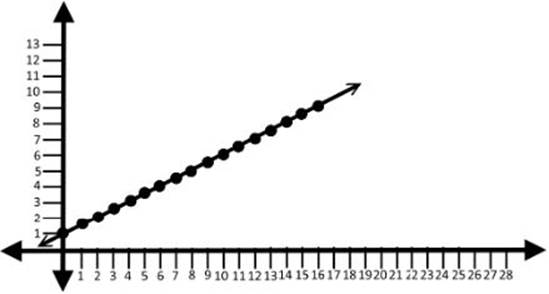
The “slope” of a linear function is a fraction that shows you how steeply the line is tilted. To find the slope of a line, choose any two points on the line. Measure the vertical separation between the two points, starting from the left-most point. The vertical separation number goes in the numerator of the slope fraction. Then measure the horizontal separation between the two points, again starting from the left-most point. The horizontal separation goes in the denominator of the slope fraction.
Example:
In our graph above, we can pick any two points on the function line to determine the slope. Let”s pick (2,2) and (8,5). The vertical separation here is the difference between 2 on the left-most point and 5 on the right-most point. So the vertical separation here is 3, and we put a 3 in the numerator of the slope fraction for this line. Now we determine the horizontal separation between 2 on the left and 8 on the right, which is 6. So a 6 goes in the denominator of the slope fraction. Now we have the numerator and the denominator of the slope fraction, and we see that the entire slope fraction is 3/6, or 1/2. So the slope of f(x) = (x/2) + 1 is 1/2. (Keep reading for a much easier way to figure out slope.)
The equation for a line will often be written in this format: y = mx + b. In fact, our function from the previous example was written in that way: f(x) = (x/2) + 1. (Remember that y and f(x) are the same thing for the purposes of graphing a function, and that “½ x” can be re-written as x/2.)
This y = mx + b format is called “slope-intercept format.” We call it that because it shows us two things right away: the slope of the function, and the “y-intercept” of the function.
The m coefficient of the x variable will be the slope.
The b constant in the function will be the point where the linear function crosses the y axis.
Example:
In the linear function f(x) = 9/7 x + 14, the m in the y = mx + b notation is 9/7, and the b is 14. This means the slope of the function is 9/7, and the point where the line crosses the y-axis is 14.
In the linear function y = -3/2 x + 2, the slope is -3/2 and the y-intercept is 2.
When two linear functions have the same slope, they are parallel.
When you can multiply the slope of one linear function by the slope of another linear function and get -1, the two linear functions are perpendicular to one another.
The SAT will never ask you to graph a linear function. It will only ask you to use graphs to figure out other information, or to identify an answer choice that correctly graphs a function.
Quadratic functions
A quadratic function is a function where the x variable has an exponent of 2.
Example:
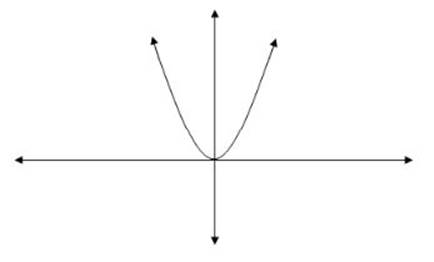
y = x2 is a quadratic function.
Quadratic functions are NEVER linear.
The SAT never asks you to draw the graph of a quadratic function. It will only ask you to use given graphs to answer questions, or to identify which answer choice correctly graphs a given function.
Quadratic functions always extend infinitely in some direction (up or down).
Example:
The graph of y = x2 extends “up” infinitely, and looks like this:
The graph of y = - (x2) extends “down” infinitely, and looks like this:
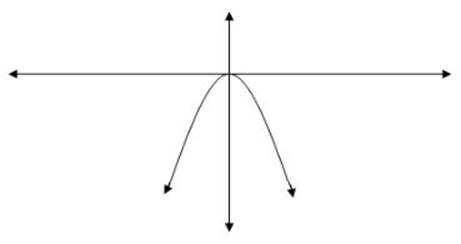
Note that the “direction” of the graph of a quadratic equation is really just a question of its range. When the range extends to negative infinity, the graph “opens down.” When the range extends to positive infinity, the graph “opens up.”
When a quadratic function “opens down,” its highest point is the (x, y) pair that has the greatest y value.
When a quadratic function “opens up,” its lowest point is the (x, y) pair that has the lowest y value.
Sometimes you”ll be asked to find the “zeros” of a quadratic function. The zeros are the points where the graph of the function touches the x-axis. To find the zeros, just set f(x) equal to zero, and then solve the resulting equation by factoring, just like we did above.
Example:
To find the zeros of f(x) = (x2)/3 – 3, we set f(x) equal to zero and then solve for x by factoring:
0 = (x2)/3 – 3
3 = (x2)/3
9 = x2
x = 3 or x = -3
So the zeros of f(x) = (x2)/3 – 3 are 3 and -3.
Points and lines
A unique line can be drawn to connect any two points.
Between any two points on a line, there is a midpoint that is halfway between the two points.
Any three or more points may or may not fall on the same line. If they do, we say the points are collinear.
Angles in the plane
Degrees are the units that we use to measure how “wide” or “big” an angle is.
Example:
This is a 45-degree angle:
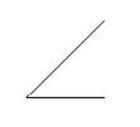
This is a 90-degree angle, also called a “right angle:”

This is a 180-degree angle, which is the same thing as a straight line:

Sometimes angles have special relationships. The two types of special relationships that the SAT cares about the most are vertical angles and supplementary angles
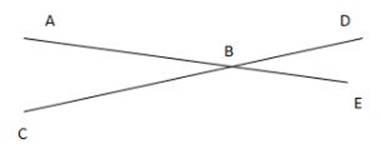
Vertical angles are the pairs of angles that lie across from each other when two lines intersect. In a pair of vertical angles, the two angles have the same degree measurements as each other.
Example:
Angles ![]() ABC and
ABC and ![]() DBE are a pair of vertical angles, so they have the same degree measurement. Angles
DBE are a pair of vertical angles, so they have the same degree measurement. Angles ![]() ABD and
ABD and ![]() CBE are also a pair of vertical angles, so they have the same measurements as each other as well.
CBE are also a pair of vertical angles, so they have the same measurements as each other as well.
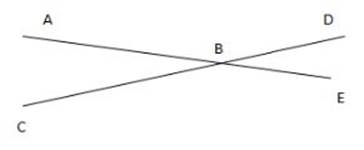
Supplementary angles are pairs of angles whose measurements add up to 180 degrees. When supplementary angles are next to each other, they form a straight line.
Example:
![]() ABC and
ABC and ![]() ABD are a pair of supplementary angles, because their measurements together add up to 180 degrees—together, they form the straight line CD.
ABD are a pair of supplementary angles, because their measurements together add up to 180 degrees—together, they form the straight line CD.
Triangles
The SAT loves to ask about triangles.
The sum of the measures of the angles in any triangle is 180 degrees, the same as it is in a straight line.
In any triangle, the longest side is always opposite the biggest angle, and the shortest side is always opposite the smallest angle.
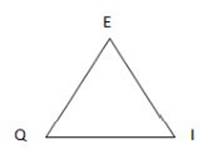
In an “equilateral” triangle, all the sides are the same length.
In an equilateral triangle, all the angles measure 60 degrees each.
Example:
In the equilateral triangle ![]() EQI below, all the sides are of equal length, and all the angles are 60 degrees.
EQI below, all the sides are of equal length, and all the angles are 60 degrees.
In an “isosceles” triangle, two of the three sides are the same length as each other, and two of the three angles are the same size as each other.
Example:
![]()
![]() In the isosceles triangle
In the isosceles triangle ![]() ISO below, side IS is the same length as side SO. Also,
ISO below, side IS is the same length as side SO. Also, ![]() SIO and
SIO and ![]() SOI have the same degree measurement as each other.
SOI have the same degree measurement as each other.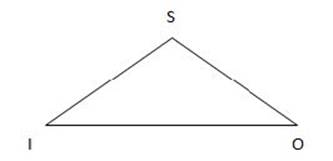
A “right” triangle is a triangle that includes a ninety-degree angle as one of its three angles.
A special relationship exists between the measurements of the sides of a right triangle: If you take the lengths of the two shorter sides and square them, and then add those two squares together, the resulting amount is the square of the length of the longest side.
Example:
In the right triangle below, a2+ b2 = c2
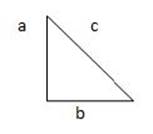
The expression of this relationship, a2 + b2 = c2, is called the “Pythagorean Theorem.”
A “Pythagorean triple” is a set of three numbers that can all be the lengths of the sides of the same right triangle. Memorizing four of these sets will make your life easier on the SAT.
Example:
{3, 4, 5} is a Pythagorean triple because
32 + 42 = 52.
{1, 1, √2} is a Pythagorean triple because
12 + 12 = √22
{1, √3, 2} is a Pythagorean triple because
12 + √32 = 22
{5, 12, 13} is a Pythagorean triple because
52 + 122 = 132
When we multiply each number in a Pythagorean triple by the same number, we get another Pythagorean triple.
Example:
If we know {3, 4, 5} is a Pythagorean triple, then we also know {6, 8, 10} is a Pythagorean triple, because {6, 8, 10} is what we get when we multiply every number in {3, 4, 5} by 2.
In a {1, 1, √2} right triangle, the angle measurements are 45o, 45o, 90o.
In a {1, √3, 2} right triangle, the angle measurements are 30o, 60o, 90o.
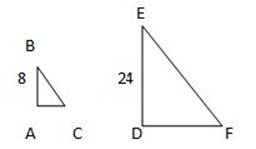
Two triangles are “similar triangles” if they have all the same angle measurements.
Between two similar triangles, the relationship between any two corresponding sides is the same as between any other two corresponding sides.
Example:
![]()
![]() Triangles
Triangles ![]() ABC and
ABC and ![]() DEF below are similar. Side AB has length 8, and side DE has length 24, so every side measurement in
DEF below are similar. Side AB has length 8, and side DE has length 24, so every side measurement in ![]() DEF must be three times the corresponding side in
DEF must be three times the corresponding side in![]() ABC.
ABC.
The formula for the area of a triangle is given in the front of every real SAT Math section.
In every triangle, the length of each side must be less than the sum of the lengths of the other sides. (Otherwise, the triangle would not be able to “close.”)
Parallelograms
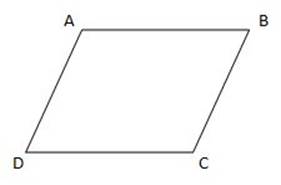
A parallelogram is a four-sided figure where both pairs of opposite sides are parallel to each other.
In a parallelogram, opposite angles are equal to each other, and the measures of all the angles added up together equal 360.
Example:
In ![]() ABCD below, all the interior angles taken together equal 360o, and opposite angles have equal measurements.
ABCD below, all the interior angles taken together equal 360o, and opposite angles have equal measurements.
Rectangles
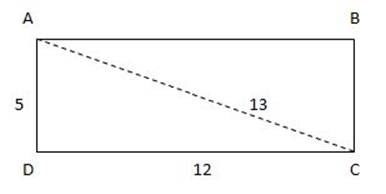
Rectangles are special parallelograms where all the angles measure 90 degrees. In a rectangle, if you know the lengths of the sides then you can always figure out the length from one corner to the opposite corner by using the Pythagorean theorem.
Example:
![]() In the rectangle below, all angles are right angles, and we can use the Pythagorean theorem to determine that the diagonal AC must have a length of 13, since 52 + 122 = 132.
In the rectangle below, all angles are right angles, and we can use the Pythagorean theorem to determine that the diagonal AC must have a length of 13, since 52 + 122 = 132.
Squares
Squares are special rectangles where all the sides have equal length.
Area
The area of a two-dimensional figure is the amount of two-dimensional space that the figure covers.
Area is always measured in square units.
All the area formulas you need for the SAT appear in the beginning of each Math section, so there”s no need to memorize them—you just need to know how to use them.
Perimeters (squares, rectangles, circles)
The perimeter of a two-dimensional object is the sum of the lengths of its sides or, for a circle, the distance around the circle.
To find the perimeter of a non-circle, just add up the lengths of the sides.
The perimeter of a circle is called the “circumference.”
The formula for the circumference of a circle appears in the beginning of every real SAT Math section. It”s C = 2pi.
Other polygons
The SAT might give you questions about special polygons, like pentagons, hexagons, octagons, and so on.
The sum of the angle measurements of any polygon can be determined with a simple formula: Where s is the number of sides of the polygon, the sum of the angle measurements is (s – 2) * 180.
Example:
A triangle has 3 sides, so the sum of its angle measurements is given by (3 – 2) * 180, which is the same thing as (1) * 180, which is the same thing as 180. So the sum of the measurements of the angles in a triangle is 180 degrees. (Remember that we already knew this!)
A hexagon has 6 sides, so the sum of its angle measurements is (6 – 2) * 180, or (4) * 180, which is 720. So all the angles in a hexagon add up to 720 degrees.
To find the perimeter of any polygon, just add up the lengths of the sides.
To find the area of a polygon besides a triangle, parallelogram, or circle, just divide the polygon into smaller triangles, polygons, and/or circles and find the areas of these pieces. A real SAT math question will always lend itself to this solution nicely.
Circles (diameter, radius, arc, tangents, circumference, area)
A circle is the set of points in a particular plane that are all equidistant from a single point, called the center.
Example:
Circle O has a center point O and consists of all the points in one plane that are 5 units away from the center:
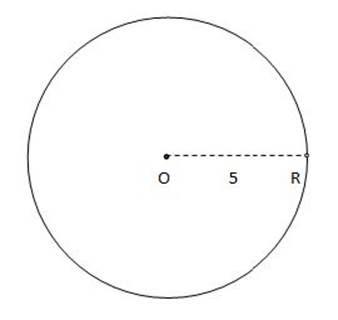
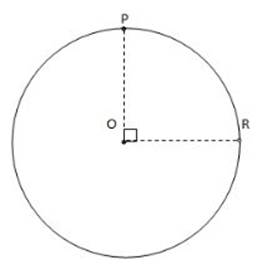
A radius is a line segment drawn from the center point of a circle to the edge of the circle at point R.
Example:
In the circle above, the line segment OR is a radius because it stretches from the center of the circle (O) to the edge of the circle
All the radii of a circle have the same length, since all the points on the edge of the circle are the same distance from the center point.
A diameter is a line segment drawn from one edge of a circle, through the center of the circle, all the way to the opposite edge.
Example:
LR is a diameter of circle O because it starts at one edge of the circle, stretches through the center of the circle, and stops at the opposite edge of the circle.
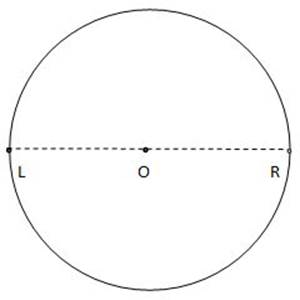
Because a diameter can be broken into two opposite radii, a diameter always has a length equal to twice the radius of the circle.
A diameter of a circle is the longest line segment that can be drawn through the circle.
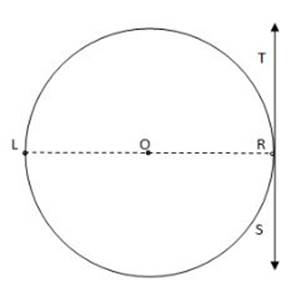
A tangent line is a line that intersects a circle at only one point.
A tangent line is perpendicular to the radius of the circle that ends at the one point shared by the tangent and the circle.
Example:
Circle O has a tangent line TS that intersects the circle at point R, and is perpendicular to radius OR.
The circumference of a circle is the length around the circle, similar to the perimeter of a polygon.
An arc is a portion of a circle. We can measure an arc by drawing radii to the endpoints of the arc, and then measuring the angle formed by the radii at the center of the circle.
Example:
Circle O has a 90o arc PR, which we can measure by measuring the angle formed by radius PO and radius RO.
The formulas for area and circumference of a circle appear in the beginning of all real SAT math sections, so there”s no need to memorize them if you don”t already know them.
Solid geometry
On the SAT, solid geometry may involve cubes, rectangular solids, prisms, cylinders, cones, spheres, or pyramids.
All necessary volume formulas will be given to you, so there”s no need to memorize them.
The surface area of a solid is the sum of the areas of its faces (except for spheres or other “rounded” solids, which you won”t have to worry about on the SAT).
Statistics
The arithmetic mean of a set of numbers is the result you get when you add all the numbers together and then divide by the number of things that you added.
Example:
The average of {4, 9, 92} is 35, because
(4 + 9 + 92)/3 = 35.
The median of a set of numbers is the number that appears in the middle of the set when all the numbers in the set are arranged from least to greatest.
Example:
The median of {4, 9, 92} is 9, because when we arrange the three numbers from least to greatest, 9 is in the middle.
If there is an even number of elements in the set, then the median of that set is the arithmetic mean of the two numbers in the middle of the set when the elements of the set are arranged from least to greatest.
Example:
The median of {4, 9, 11, 92} is 10, because the number of elements in the set is even, and 10 is the average of the two numbers in the middle of the set.
The mode of a set of numbers is the number that appears most frequently in the set.
Example:
The mode of {7, 7, 23, 44} is 7, because 7 appears more often than any other number in the set.
Probability (elementary and geometric)
The probability of an event is a fraction that describes how likely the event is to happen. If the fraction is closer to 1, the event is more likely to happen; if the fraction is closer to zero, the event is less likely to happen.
To determine the fraction, you first calculate the total number of possible outcomes and place this number in the denominator of the fraction; then, you determine the number of outcomes that satisfy the event”s requirements, and place this number in the numerator of the fraction.
Example:
The probability of rolling a 3 on a normal 6-sided die is 1/6. There are 6 possible outcomes, so 6 goes in the denominator of the fraction. Out of those 6 outcomes we only want one, the one where a 3 comes up, so 1 goes in the numerator of the fraction.
The probability of rolling an odd number on a normal 6-sided die is 3/6. Again, there are 6 possible numbers we might roll, so 6 is our denominator. But now, since we want any odd number, the numbers 1, 3, and 5 all satisfy the requirements of our event, so there are 3 possible outcomes that we”ll be happy with—that means 3 goes in the numerator.
Probability fractions can be manipulated just like any other fractions.
To find the probability of two or more events happening in a sequence, we just find the probabilities of each event by itself, and then multiply them by each other.
Example:
The probability of rolling double-sixes on two normal 6-sided dice is 1/36, because the probability of rolling a six on either die is 1/6, and (1/6)(1/6) = 1/36.
Conclusion
We”ve just covered all the math concepts that the College Board will allow itself to cover on the SAT. As I mentioned at the beginning of the Toolbox, it”s important to keep in mind that simply knowing these concepts is not enough to guarantee a good score on the SAT. It”s much more important to focus on the design of the SAT Math section and learn how to take apart challenging questions.
And that”s exactly what we”ll start talking about on the next page . . .