The SAT Prep Black Book
SAT Math
A Selection of Challenging Questions
At this point we”ve taken a look at a variety of Math questions, but you”re probably interested in seeing more. I understand where you”re coming from with that, and I”m about to show you some more Math solutions, but . . . before I do, I want to make sure I reiterate what you should be learning from each solution.
I am NOT doing these solutions in an effort to show you something formal that you should memorize and then expect to repeat on future SAT Math questions, as we would normally do for a math class in school. Remember that the SAT Math section will show you very strange combinations of very basic ideas, and specific questions and questions “types” are not repeated for the most part. The odds are that when you take the SAT for real, you”ll see a whole test full of math questions that don”t look like any other SAT Math questions you”ve ever seen before, at least not on the surface. And this will be the case no matter how many practice SAT Math questions you work on beforehand. Every test combines the same basic stuff in new ways.
You may have noticed I”m repeating this idea a lot. There”s a reason for that:
It”s very important, and most people ignore it.
So if you want to get better at SAT Math, the goal is to learn the underlying process, and to practice using it against real SAT Math questions written by the College Board. That”s why I”ve included these solutions: to give you an idea of the right general approach so you can continue to refine your instincts, not to give you cookie-cutter instructions for specific question types, because specific question types basically don”t exist on the SAT Math section, practically speaking.
With that important reminder out of the way, let”s take a look at some of the SAT Math questions that students have typically asked about.
As with other question explanations in this book, you”ll need a copy of the second edition of the College Board”s Official SAT Study Guide (otherwise known as the Blue Book) to follow along. Let”s get started.
Page 399, Question 11
As with many SAT Math questions, there are basically two ways to do this: we can pick a concrete number that satisfies the requirements for k and then look to see what happens to k + 2, or we can think in the abstract about properties relating to the concept of remainders. In general, abstract solutions will be faster to reach but harder for many students to execute, while concrete solutions will give most students added confidence but end up taking more time. For this particular question, though, the amount of time spent on each solution is likely to be roughly the same.
If we go the concrete route of picking a number to be k, we have to make sure that it satisfies the setup. In this case, a number like 13 would work, because 13 divided by 7 gives a remainder of 6. So then we'd look to see what happens when we divide 15 by 7, since 15 is 2 more than 13; the result is a remainder of 1.
The other way to do this is to think in the abstract: if k has a remainder of 6 when it's divided by 7, then k is 6 more than some multiple of 7, and k + 2 will be 8 more than that multiple of 7. We know that 8 is more than 7, so one more 7 will "fit in" when k + 2 is divided by 7, and we”ll be left with a remainder of 8 - 7, or 1.
Either way, (B) is the right answer.
Of course, you wouldn”t need to do both solutions on test day. I”m just doing both of them to show that there are a variety of ways to attack this question successfully, as will be the case for most SAT Math questions.
Page 400, Question 17
This is one of those questions that lets us work on identifying a whole variety of the patterns and rules we talk about in this book.
First, we”d want to notice that the diagram is drawn to scale. That means that we might be able to figure out the answer by eyeballing the diagram—or, at the very least, we want to make sure that our final answer makes sense in the context of the scale of the diagram.
Also notice that the diagram and the answer choices have a lot of expressions with √2 in them. We know that √2 relates to 45o-45o-90o triangles, which seems relevant to the question since ABC, ADB, and BDC are all 45o-45o-90o triangles.
There are a variety of ways we could try to figure out the area of the shaded region. The most straightforward way is probably to work out the distance of EF, along with the distance from F to the base of the figure, and then multiply those two things together, since they would represent the length and the height of the rectangle. We might do that by realizing that BE and BF are each 5√2 units long, and that they are each the legs of a 45o-45o-90o triangle with EF as its hypotenuse. Since the ratio of the sides of a 45o-45o-90o triangle is 1:1:√2, the distance of EF is 5√2(√2), which is 10.
Since the shaded region is divided into two squares, we know that the distance from E or F to the base of the figure must be 5. So the shaded area is 50, because we multiply 10 (the length) by 5 (the height) to find the area. So (C) is correct.
There are other ways to get this answer, as well. We could also realize that AC must be 10√2(√2), or 20 (again because of the 1:1:√2 ratio for sides of a 45o-45o-90o triangle). Then we could realize that the height of triangle ABC must be 10 (because BD is one of the legs for which BC is a hypotenuse, and this is another 45o-45o-90o triangle for which the 1:1:√2 ratio applies). That means the area of the entire triangle ABC must be 100 units. The shaded region represents 1/2 of the area of ABC (we know this either by eyeballing the scaled diagram, or by realizing that the four unshaded small triangles are the same total area as the shaded rectangle).
Now let”s turn to the answer choices. An awareness of the patterns that frequently appear in answer choices on the SAT Math section would help us to realize that 50 looks like a very likely option to be the correct answer. It fits the halves-and-doubles pattern and it”s also the middle number in a series (the series is 25, 50, 100). It also doesn”t have √2 in it, which is probably good because 3 out of the 5 choices don”t have √2.
Page 423, Question 11
Like most SAT Math questions, this one rewards us for reading very carefully and thinking about the definitions and properties of basic terms.
We”re told that 2 of the faces are black and the rest are white; this means there must be 4 white faces, since the total number of faces on any cube is 6.
If the total area of the white faces of the cube is 64 square inches, and if there are 4 white faces, then the total area per face is 64/4, or 16.
That means each face is 16 square inches. And since the dimensions of a cube are all identical, that means each face is a 4 x 4 square, which means the cube is 4 inches in each dimension.
The volume of the cube, then, is 4 x 4 x 4, or 64. So the correct answer is (A).
Notice that some of the answer choices differ from the correct answer by a factor of 2 or 4. This is a strong, strong reason to go back over your work and check it for small mistakes. If we misread the setup, or if we accidentally mis-multiplied or mis-divided, we can easily be off from the right answer in a way that will be accounted for in the answer choices. Also notice that (B) is 5 x 5 x 5, and (D) is 6 x 6 x 6. This reinforces our belief that we should find the correct answer by cubing something, but it also means we have to make sure we were right to cube 4 instead of 5 or 6.
Page 424, Question 14
As will often be the case on the SAT, there are multiple valid approaches to this question. If we wanted to use a simple permutation solution, we could realize that there are 5 options for one color, and 4 options for the other color (there are only 4 options for the second color because we”re not allowed to repeat the selected color—otherwise there would be 5 options for both). 5 x 4 = 20, so there would be 20 possible arrangements.
But the SAT doesn”t make us do things like this in the formal way—the SAT doesn”t care how we get the answer, as long as it”s right. So, if we want, we can just list out the different possible arrangements and then count them up. (To be clear, this list-and-count approach will take a good bit longer than we would normally like to spend on a question, but it can be a very concrete way to arrive at the answer if you don”t feel comfortable with permutations. Remember, too, that the reason we try to go through most questions as quickly and efficiently as possible is so that we can have more time if we need it on questions like this.)
So if we call the colors a, b, c, d, and e, and then list things out, here are the different arrangements:
zone 1 / zone 2
a/b
a/c
a/d
a/e
b/a
b/c
b/d
b/e
c/a
c/b
c/d
c/e
d/a
d/b
d/c
d/e
e/a
e/b
e/c
e/d
That means there are 20 different arrangements, so (B) is correct.
Page 457, Question 20
Most people try to approach this using some variation on the slope formula (which is
(y2 – y1)/(x2 – x1), not that I recommend it here).
But we have to remember that this is the SAT, and the College Board often likes to leave short cuts hidden in the questions for people who think to look for them.
Instead of going through the hassle of working out the slope of the original line, the slope of the perpendicular line, and the missing y-value that would make the whole thing work out correctly, let”s take a second and actually notice the answer choices for a minute.
Remember that we always want to check out the answer choices before we commit to a course of action. They”ll help us understand a lot of stuff in a lot of questions if we just pay attention to them a little.
In this case, I”m noticing that the answer choices are kind of falling into 3 different groups, in a sense. We have negative numbers, then we have 2 and 3, and then we have 5. Hmmmm.
Let”s try actually plotting line l and see what it looks like. Here”s a rough approximation of the situation described in the question:
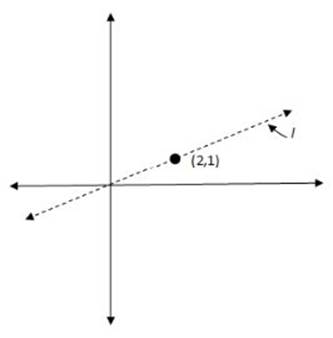
If we plot the points (0,0) and (2,1), and then think about the options offered by each of the answer choices, we might start to notice something. (A) and (B) clearly don't work if you're trying to draw line that would go through either value and (2,1), and be perpendicular to the existing line:
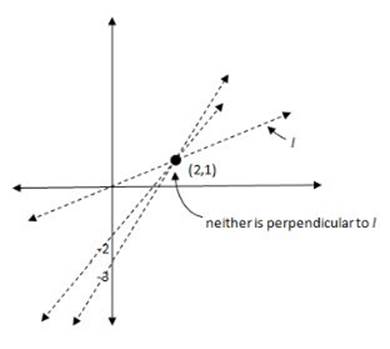
The values for (C) and (D) don”t work, either:
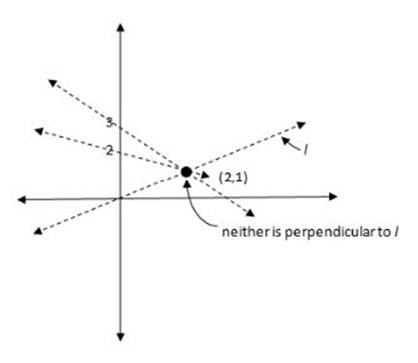
Only (E) is in anywhere near the proper place to create a line that passes through (2,1) and is perpendicular to the original line l. So (E) must be right:
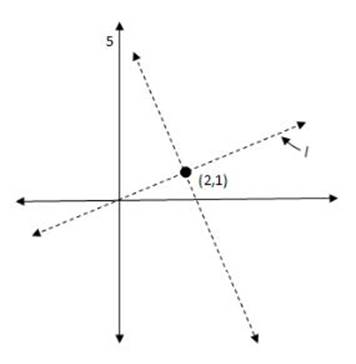
(I realize that none of the diagrams I supplied is exactly to scale, but the diagrams you would draw for yourself in your test booklet would also be out-of-scale. During the test, the point isn”t to create a perfectly scaled drawing, but to get a solid idea of where the different elements of the question would be relative to one another.)
So, as we”ve just seen, it”s possible to solve this question, which is the last one in the section and which was missed by a lot of people, without ever using any kind of formula or consulting a calculator or even adding two single-digit numbers. All we had to do was remember to notice the answer choices, plot a few points (or even just think about plotting some of them), and then realize that only one answer choice was close to working.
Notice that the College Board could have made this question much harder by including wrong answers that were closer to the right answer, or by changing the overall scale of the question. But they didn”t. They left a shortcut for alert test-takers to seize. Remember that, and look for these kinds of things on other questions.
Page 464, Question 6
People mess this question up all the time, but it”s really just a pretty straightforward application of the concept of slope. We know that for two reasons: the first one is that the diagram shows a diagonal line with its horizontal and vertical changes marked off, and the second reason (perhaps a bit more obvious) is that the question includes the word “slope.”
Remember that slope, by definition, is the ratio of the vertical change to horizontal change. That means that, in this case, for every 7 units of vertical change there are 16 units of horizontal change. If we only have 3.5 units of vertical change, then we need 8 units of horizontal change to maintain the ratio, because 3.5 is half of 7 and 8 is half of 16. So the correct answer is (A).
Notice that one of the wrong answers is 32, which is what we get if we accidentally double 16 instead of cutting it in half.
Page 468, Question 15
I often talk about how the College Board likes to mislead you by making questions seem to be something they”re not. This question might be one of the all-time best examples of that technique. It starts out looking like a classic probability question, one of those situations where somebody has a certain number of things in a bag and you have to calculate the chance that they”ll pull a certain kind of thing out of the bag at random.
But that”s not what it is at all. Instead, it”s much simpler than that, but it”s unlike anything that any test-taker has probably ever seen before.
This is one more example of why you can”t take anything for granted on the SAT. Everything needs to be read carefully.
Ari starts out with 3 red things and 4 green things. If he takes 13 more pieces and we need to end up with more reds than greens, we might imagine that the 13 is made up of 7 reds and 6 greens, just as a place to start; if that's the case, then there would be 10 red and 10 green, which doesn't satisfy the requirements of the question. So in order to end up with more reds than greens, Ari would need to pull out at least 8 reds, so the answer is 8.
Again, there's absolutely no formula for this, and it has nothing to do with probability. It's just reading and thinking. Most SAT Math questions are just reading and thinking.
Page 468, Question 16
A lot of people who see this question immediately start worrying about the word “tri-factorable,” as though it were a real math term instead of something that the College Board made up specifically for this question.
There are two ways that we can figure out that the word “tri-factorable” was just made up for this question. The first way is that the question tells us what the word means: a tri-factorable number is one that is the product of 3 consecutive numbers. (If this were a real math term, the College Board wouldn”t bother to define it. For slope questions, they don”t say, “What is the slope of this line, if slope is defined as blahblahblah,” because you”re supposed to know what slope is, because slope is a real math concept.)
The second way that we can know this is a made-up word is to be familiar with what the SAT is allowed to ask us about when it comes to math. The SAT can only ask about the concepts in the toolbox in this book, and the toolbox doesn”t cover tri-factorability.
So it must just be that we”re supposed to figure out what the word means from reading the question. If we know what the words "product" and "consecutive" mean, then we know what a tri-factorable number is. Remember, as always, that the most important skill on the SAT is reading carefully.
Now, let”s proceed.
We know that all of these questions can be answered in less than 30 seconds, and we know that it would clearly take a lot longer than 30 seconds to attempt to tri-factor each of the first 1,000 integers.
So there must be another way to go.
It”s important to remember that we can always just list out the answers to these kinds of questions that ask how many numbers in a certain set satisfy a certain condition. Either we”ll start listing them and realize there”s only a small number of them, or we”ll start listing them and realize there”s a certain pattern they all follow, and then we can predict the final number from the pattern.
So how can we figure out a tri-factorable number? Since they”re made by multiplying consecutive integers, I”d start with the smallest positive integer and see what happens:
1 * 2 * 3 = 6
So if we start with 1 as the first positive integer, we arrive at the product 6, which must be the first tri-factorable number.
The next tri-factorable number will start with 2:
2 * 3 * 4 = 24
From there we can basically get on a roll:
3 * 4 * 5 = 60
4 * 5 * 6 = 120
5 * 6 * 7 = 210
6 * 7 * 8 = 336
7 * 8 * 9 = 504
8 * 9 * 10 = 720
9 * 10 * 11 = 990
10 * 11 * 12 = 1320
Oops—notice that that last number is bigger than 1000! So there are 9 numbers that work: the one I get when I multiply three consecutive numbers starting with 1, the one I get when starting with 2, starting with 3, with 4, with 5, 6, 7, 8, and finally 9, and that's it.
Notice that this question, like so many other “challenging” SAT Math questions, involves nothing more than careful reading, basic arithmetic, and a willingness to play around with familiar concepts in strange ways. This is typical for the SAT, as we”ve seen many times by now and will see again.
Notice also that there are many ways to mess this question up. We might miscount, or accidentally overlook one or more of the tri-factorable numbers. Any one of those tiny mistakes will cause us to miss the question completely.
Page 468, Question 17
This is another one of those questions that we could try to answer in a few different ways. Many people will attempt an algebraic solution, or you could also try guessing and checking. There”s also another approach we”ll talk about after I go over the algebraic one.
For call A, the cost will be $1 + $0.07(t-20).
For call B, the cost will be $0.06(t).
So just set them equal and solve:
$1 + $0.07(t-20) = $0.06(t) (initial setup)
1 + .07t - 1.4 = .06t (distribute $0.07 on the left)
1 - 1.4 = -.01t (combine like terms)
.4 = .01t (simplify the expression on the left)
40 = t (isolate t)
The faster approach is a little more holistic, and would probably not be tried by most test-takers, even trained ones. Still, I thought we should talk about it. To work this problem out without really writing out any algebra, we could realize that the $1 for the first 20 minutes works out to 5 cents per minute, which is one cent per minute less than the other rate. After those 20 minutes are up, the rate goes to 7 cents per minute, which is one cent per minute more than the other rate. So to get everything to equal out, you'll need 20 more minutes of talking at the higher rate after the initial 20 minutes of talking at the lower rate. 20 + 20 is 40, so 40 is the answer.
Just to be clear, both approaches are equally valid, of course. I just wanted to introduce the second one as an exercise of sorts, to keep calling your attention to the fact that the College Board usually sets up SAT Math questions so that they can be attacked quickly and easily if we know how to look at them.
Page 468, Question 18
This question is rated 5 out of 5 for difficulty, but, of course, we know that that doesn”t mean much. All it means is that a lot of untrained people missed it. As we”ll see in this explanation, this is yet another SAT Math question that requires nothing more than careful reading and careful thinking.
We”re told the perimeter is p, and we know that each square has a side of k. The perimeter consists of 16 sides, so the perimeter”s length is 16k.
The area of each square must be k2, and there are 10 squares. So the area is 10k2.
Since the question says that p and a are equal, we know that
16k = 10k2
Solving, we get
16 = 10k (divide through by k)
1.6 = k (isolate k)
And that”s all. Notice that this question only required us to know the definitions of the word “perimeter” and “area,” and basic algebra. There was no formula involved, apart from the formula for the area of a square, which the test provides for us at the beginning of the section. There was also no real need for a calculator, since the question only involves dividing by 10, which we can accomplish by moving the decimal point.
Again, these attributes are pretty typical of the “hardest” SAT Math questions.
Page 483, Question 8
This question stumps a lot of people. In my experience, almost everybody who misses it does so because they don”t read it carefully, or they don”t notice the answer choices.
If the probability of choosing red is 3 times that of choosing blue, that means that there are 3 times as many red beads as there are blue beads. Since there are 12 red beads, then, there must be 4 blue beads. Further, the number of glass beads altogether is 4 times the number of wooden ones, so if there are 16 total glass beads (12 red and 4 blue), then there are 4 wooden ones. Adding that all up, we get that there are 20 beads.
That”s the more mathematical way to approach this.
But an easier way to think about this might be to realize that there are more red beads than anything else, and there are only 12 of those, so 45 is already way too big of a number, and anything bigger than 45 is obviously also way too big. That means the only answer choice that can possibly work is (A).
Remember to pay attention to details and answer choices!
Page 485, Question 12
This is another SAT Math question that a lot of people struggle with, even though it only involves one of the simplest ideas in all of geometry: the idea that there is an infinite number of points in a circle (or in any geometric figure).
I think the easiest way to approach this is to say that every single point on the circumference of the circle could be a point that served as the corner of a rectangle like the rectangles in the original diagram. So there is an infinite number of rectangles with perimeter 12 that can be inscribed in the circle. Since infinity is bigger than 4, we know that the answer is (E).
Page 486, Question 15
For this question, once more, I would just read the question carefully and think about what it's describing.
20% of Tom's money was his spend on the hotel. He spent $240 overall, so he spent $240 * 0.2 = $48 on the hotel.
If he only paid for 1/4 of the hotel, then the hotel cost $48 * 4, or $192.
The fact that the last three answer choices all differ from one another by $48 should alert us to the fact that we need to be really careful here, because there are ways to misread or miscalculate and end up on either wrong answer. The far most common mistake is to misread the thing about sharing with 3 other people, and treat it like it just says the room was split among 3 people.
This is one more situation in which paying attention to the relationships among the answer choices can alert us to mistakes that the College Board wants us to make, and can reassure us that (D) is the correct answer.
Page 486, Question 16
Like many other SAT Math questions, this is one that manages to be fairly challenging even though it only involves basic arithmetic. It”s also a question that will require very careful reading, and a question for which there is no ready-made formula. In other words, it”s a typical SAT Math question.
So let”s just think about what the question is describing, and how we might figure out what it”s asking us.
One approach would be to try to make a square board that would have a number of border tiles somewhat near each answer choice, and see if only one answer choice can be made to work like that. This will be a little tedious, and probably extremely time-consuming, but it will work if we do it right:
(A) doesn't work--if there are 10 on the boundary, it couldn't be 3 x 3 or 4 x 4.
(B) doesn't work either. 7 x 7 would give you 24.
(C) doesn't work because 9 x 9 would give you 32.
(D) doesn't work because 11 x 11 would give you 40.
(E) works because if the board is 14 x 14 there are 52 tiles on the border.
Another approach, possibly slightly faster, is to try drawing out a few small game boards to see if we can figure out some kind of pattern that would help us eliminate all the wrong answer choices.
If, for instance, n = 2, then the square would look like this:

In this case, the number of things on the boundary would be 4.
If n is 3, then the board looks like this:

In that case, the k number is 8.
And so on. Now we need to try and understand what's going on here. Basically, k must always end up being a multiple of 4. So we need an answer choice that's a multiple of 4. Only (E) is.
There are other valid approaches here as well, but I think those two will be the ones that most people find.
This question presents me with another opportunity to remind you of what”s important to take away from these discussions. The goal of going over this solution is not to teach you a formal way to approach questions that ask about the border tiles on square game boards, because there will never be another SAT Math question that asks about the border tiles on square game boards.
Instead, the goal of going over this question is to deepen your understanding of the principles of SAT Math in general. There”s no way to predict exactly what kinds of things you”ll see on test day, but if we come to understand the importance of reading carefully, thinking about the answer choices as part of the question, and so on, then you”ll be able to take apart whatever weird combinations of basic facts the SAT presents you with. So it”s not about memorizing rigid steps for certain types of questions. It”s about developing a general feel, and confidence that you can work out whatever they throw at you by relying on the test”s design principles.
Page 518, Question 17
Just about everyone panics for a second when they run into this question, because it seems to be asking us to figure out the area of a shape we”ve never seen before. This is one of those moments when knowing the unwritten rules of the test really comes in handy. Remember that the College Board can only ask you to find the areas of rectangles, triangles, and circles, and it gives you the formulas for those areas at the beginning of each SAT Math section.
So if a question looks like it's asking for the area of something else without giving you another area formula to use, then that something else can always be expressed in terms of rectangles, triangles, and circles. Always.
In this case, it”s probably pretty clear that we can”t use triangles and rectangles, because there are no corners in this figure. So we”ll have to figure out the area of these figures as though they were circles.
But how can we do that?
I think the easiest way is to imagine reversing the bottom half of the big circle from left to right, so that the bottom half of the circle becomes just a reflection of the top half, and we're left with 3 circles, all tangent to each other on their left-most points. It would look something like this:
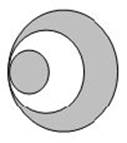
So now we have to find the areas of those circles, and add and subtract them appropriately. If AD is 6, then each of those dots is 1 unit from the dot before it or after it. That means the radius of the smallest circle is 1, so its area is pi. The radius of the biggest circle is 3 units, so its area is 9pi. The radius of the medium circle, the unshaded one, is 2 units, so its area is 4pi.
So we want the amount equal to the area of the biggest circle minus the area of the medium circle plus the area of the smallest. So it's 9pi – 4pi + 1pi, or 6pi. Which means (C) is correct.
This is just one more example of a question that seems a lot more exotic than it is. If you remember the rules the College Board has to play by, then you”ll find a lot of things much easier than most people will. An untrained test-taker will throw up his hands in frustration over this question, but a trained test-taker knows how to turn it into a simple question about circles, and then solve it using the basic formula provided in the beginning of each SAT Math section.
Page 519, Question 18
For this question, I would just draw 6 points out so that no 3 are on a line together, and then try connecting them: basically, each of the 6 points connects to the other 5. We can count the lines up after drawing them out, or we can try doing a little multiplication.
If we multiply, it might seem like there should be 30 lines, since 6 * 5 = 30, but we have to remember that each line touches two of the points. So there aren”t actually 30 lines, because each line counts as a connection for both of the points. In other words, if we call the points A, B, C, D, E, and F, then the line from A to B is the same line as the one from B to A.
So we want to divide the 30 apparent connections by 2 in order to compensate for the fact that each line serves as one connection between 2 points, so we don”t double-count the lines. That gives us 15 for our final answer, so (A) is correct.
Note the patterns in the answer choices: 15 is half of 30, and there's also 36 and 18 (36 would be 6 x 6 instead of 6 x 5, and 18 is half of that). Once more, the answer choices help point us in the right direction and make us aware of potential mistakes that could be easily made.
Page 519, Question 19
This question often blows people away because it seems much more complicated than it actually is—which, as we”ve said many times, is typical for SAT Math questions in general. As usual, we”ll approach this by reading carefully and thinking carefully.
First, it”s important to realize that the question tells us that a and b are equal, so f(a) and f(b) must also be equal.
We also want to remember that questions with roman numerals for answer choices are often based on abstract properties.
Finally, we want to remember that we don”t need to know what the actual function is. All we need to know is that it has the property that f(x + y) = f(x) + f(y).
So now let”s try to reframe each Roman numeral in terms of that property, and see if we can do it:
For I, 2f(a) = f(a) + f(a) = f(a + a) = f(a + b). We can substitute b for a at the end to arrive at f(a + b).
For II, f(a) * f(a) has nothing to do with what the question told us about; the question only told us about an additive property of the functions, not a multiplicative one. So we can”t substitute or manipulate anything further here.
For III, f(2a) = f(a + a) = f(a) + f(a) = f(b) + f(b). So this one works too.
So we can see that (C) works because roman numerals I and III are valid statements given that
f(x + y) = f(x) + f(y).
This is a question that won”t allow us to use a concrete example (unless you get extremely lucky in making up a function for f). The only practical way to approach it is to make substitutions and follow the rules of algebra to see which roman numerals contain valid equations.
For most test-takers, this will be one of the hardest questions. So this is a good time for me to remind you that your primary goal probably shouldn”t be trying to improve your performance on the occasional tough question like this; it”s much more important to make sure you lock down all the questions that seem easier first. Once you get to a point where you never make any “careless” errors, you should feel free to start worrying about questions like these. But if you try to tackle these kinds of questions without first making sure that you”re executing correctly on the questions you can handle more comfortably, you”ll just be wasting your time, and your score won”t improve.
I”m not saying that a question like this can”t be answered, or that if follows different rules. This question can be solved with basic math and careful thinking, just like every other SAT Math question. I”m just saying that it”s important to focus on eliminating mistakes before you focus on figuring out questions that seem more challenging to you.
Page 519, Question 20
This question really helps drive home the importance of considering the answer choices along with the rest of the question.
When we look at the answer choices, we can see that they all involve y, with no x. That means we need a way to express x in terms of y. The only way to do that is to realize that x times y is 4000, since that's the area of the rectangle. So x is 4000/y.
Furthermore, the total length of rope needed is y + 4x, because there are 4 vertical line segments with length x in the diagram.
We can re-write y + 4x as y + 4(4000/y), which is the same as y + 16000/y. So (B) is correct.
When I look back over the other answer choices, I would definitely want to notice that more of the answer choices include 3y than just y in the denominator, and that would worry me for a second, because I know that elements of the correct answers tend to appear in wrong answers in questions like this. So I would double-check my work again.
Page 527, Question 8
Despite my general dislike of algebra for the purposes of SAT Math solutions, sometimes it can”t be avoided, and I think this question represents one of those times for most test-takers. This question is also one of those questions that can be expected to take most test-takers more time than usual. It”s because of questions like this that we have to try to work through other questions as quickly as possible without sacrificing accuracy.
For most people, the obvious first step will be to multiply out the expression on the left (using FOIL), which gives us this:
(x-8)(x - k) = x2 - kx - 8x + 8k
In terms of what we would normally get from FOIL-ing out two binomials, this expression is a little odd, because it has two terms with x instead of one. (This is because the original binomials involved more than one unknown value—they had a k in addition to the x-es.) So let”s try to fix that by combining 8x and kx:
(x-8)(x - k) = x2 - kx - 8x + 8k
(x-8)(x - k) = x2 - (8 + k)x + 8k
Now it looks a bit more normal—we”re still stuck with that weird k, but at least now we have one term with x2, one term with just x, and one term with no x at all, which is our normal arrangement after FOIL-ing out two binomials.
So now our entire equation looks like this:
x2 - (8 + k)x + 8k = x2 - 5kx + m
Now we realize that (8 + k)x must correspond with 5kx, and that 8k corresponds with m. In other words, the two x terms on both sides must correspond, and the two terms on both sides with no x at all must also correspond. So we can solve for k, and then use k to solve for m:
(8 + k)x = 5kx (deal with the k terms on both sides first)
(8 + k) = 5k (divide both sides by x)
8 + k = 5k (simplify)
8 = 4k (combine like terms)
2 = k (isolate k)
and, therefore:
m = 8k and k = 2
m = 8(2) (substitute 2 for k)
m = 16 (simplify)
So (B) is correct.
That”s the algebraic approach. It”s kind of ugly, at least by SAT standards, but it works.
There”s another approach we can use that will probably be a little easier on our brains, though it might not be any faster. That would be to look at each answer choice and try to solve backwards; only one of the choices will make this possible.
For instance, if we want to test out choice (A), we would see what has to happen if m is 8. Since m is the product of 8 and k, according to FOIL, then we know that k would have to be 1 if we made m be 8. But if we FOIL out the expression on the left with k equal to 1, the rest of the expression doesn”t end up matching with the rest of the expression on the right.
Then we could try with (B), (C), and so on. We would see that the process can be made to work when m equals 16, but not for any other choice.
Another way to go, which is probably faster, but which requires a bit more awareness of algebra, is to notice the relationship between m and 8k, and the relationship between 8x, kx and 5k. Basically, we can see that k must be a value such that 8+k and 5k are equal, which means k must be 2, as we figured out before. And that would mean that m has to be 16.
Again, this is one of the ugliest questions in the book, but we can work out the answer if we stick to the fundamentals of algebra, and if we”re willing to play around with an unfamiliar presentation of those fundamentals.
Depending on the approach you take, this question might eat up a little (or a lot) more time than the average SAT Math question. While we should always try to find the most efficient solutions during practice sessions, remember that it”s normal for some questions to take longer than others on test day. Questions like this one are a big part of the reason why it”s so important to try to save time on questions that seem easier to you. That way, you have enough time left to play around with the harder questions, or to go back over your work and check your answers.
Page 530, Question 18
This question is a little complicated for an SAT Math question, but, as trained test-takers, we expect that we might see a little more complication in the last question or two of the grid-in section. As always, we”ll pay close attention to what the question is asking and see what we can figure out.
This question asks about the value of a, and the only place in the whole question where we can find any reference to a is in the expression y = ax2. So that means we”re going to need values for y and x that we can plug in to that expression, so we can solve for a.
Apart from (0,0), which won”t help us figure out a, there are only two points on the graph that have (x,y) coordinates we can probably figure out: points Q and R, which are also in square PQRS.
We”re told that PQRS has an area of 64. We know this is an important dimension to be aware of because it was included in the text of the question after being omitted from the diagram itself. If the area is 64, that means each of the square”s sides is 8 units long. And that, in turn, means that point R is located at (4,8), because OS is half of PS.
Now we have values for x and y that we can plug in for point R, which is on the graph of y = ax2:
y = ax2 (given equation for the graph)
8 = a(42) (substitute x and y values for the point (4,8))
8 = 16a (simplify expression on the right)
8/16 = a (divide both sides by 16 to isolate a)
1/2 = a (simplify expression on the left)
Notice that all of the ideas in this question are relatively simple ideas on their own; the trick was to trace the proper approach back through the wording of the question to figure out how to string together the relevant ideas.
Notice, also, that this question is actually very similar to question 18 on page 717 of the College Board”s Blue Book. (The two questions aren”t identical, but the only real difference between them is that ABCD isn”t a square in that other question, and the function in this question isn”t a parabola.) Do not be misled by this coincidence into assuming that the College Board frequently repeats a limited number of question types in each SAT Math section. On the contrary, in the entire Blue Book these two questions are among the only examples of question material being repeated so closely on the SAT Math section.
Page 547, Question 13
When you have a question like this where the answer choices are all relatively small numbers, that's a sign from the test that counting the options is the best way to go. On the other hand, if the number of options was much higher, that would be a sign that there's a solution where you don't actually have to count things.
From the beginning, though, we want to notice that each answer choice is only one more than the choice before it, so if we make a very small mistake and end up overlooking one of the possible combinations, or accidentally counting a combination twice, there will be a wrong answer choice waiting for us. Remember that it”s always very important to pay attention to small details on the SAT, but it”s especially important on questions like this.
So at this point I would go ahead and list the possibilities systematically, to make sure I don't skip anything. In this case, I would start with the smallest-value tokens and then work up from there.
oSeventeen 1-point tokens
oTwelve 1-point tokens and one 5-point token
oSeven 1-point tokens and two 5-point tokens
oSeven 1-point tokens and one 10-point token
oTwo 1-point tokens and three 5-point tokens
oTwo 1-point tokens, one 5-point token, and one 10-point token
So the answer is (E), six.
Normally I would be suspicious of liking the largest answer choice in a series, because the College Board usually likes to make the correct answer be somewhere in the middle of a series if one appears in the answer choices. So I would double-check my counting to make sure that everything I listed was really valid.
I”d also like to reiterate that this question is a great example of how SAT math can be "tricky" rather than really difficult. There's no advanced math concept or common formula involved here or anything, just a simple arithmetic issue where it's very easy to get mixed up and overlook some options.
Page 548, Question 16
This question involves a lot of geometric concepts, but as long as we think through them carefully we should have no problem navigating it—after all, since this is the SAT Math section, all of the individual concepts involved must be fairly simple on their own, even if they”re combined in ways that might be strange.
The first idea mentioned in the question is that of a cube with volume 8. If the volume is 8, then the side length of the cube must be 2, because 2 cubed is 8.
Then we”re told that the cube is inscribed in a sphere. That”s a hard thing to represent with a diagram on a two-dimensional page, so let”s describe it with words instead: think of a throwing die stuck inside a ping-pong ball so that it can”t move.
Now the question asks for the diameter of the sphere. Since we were only given one numerical measurement in the entire question (the volume of the cube), it must be possible to figure out the diameter of the sphere from some measurement related to the cube.
At this point, we need to realize that the distance from one corner of the cube to the very opposite corner of the cube (in other words, the distance to the corner on the other side of the center of the cube) is the same as the diameter of the sphere. I”ll make a diagram and leave the sphere out of it so you can see the distance I”m talking about. The dashed line is the distance we want to find:
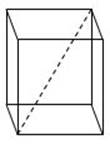
To find this distance, we have to use the Pythagorean theorem twice. First, we”ll use it to find the distance of the diagonal across one of the faces of the cube; next, we”ll use that diagonal as a leg to find the actual corner-to-opposite-corner distance we”re looking for. So here”s step 1:
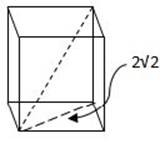
That diagonal across the bottom face is the hypotenuse of a 45o-45o-90o triangle with legs of length 2, so its length is 2√2.
Notice that the diagonal of 2√2 now forms the leg of another right triangle whose hypotenuse is the distance we”re looking for, and whose other leg is one of the vertical edges of the cube.
This new triangle then has legs of 2√2 and 2, which means the hypotenuse is the square root of the sum of 2√22 and 22. That sum is 12, so the hypotenuse is the square root of 12, which we can simplify like this:
√12 = √4 * √3
= 2√3
So (D) is correct.
I would like to add that I have always felt like there is a much simpler way to approach this question, but I don”t quite see it. Note that the values in the answer choices are all pretty well spread out from one another, for the most part—I”m pretty sure there”s something we”re supposed to be able to notice from the setup that might let us realize that the correct answer must be a value between 3 and 4 or something. The reasoning would go something like this: 2 is much too small to be the distance across the cube because it”s already the side-length of the cube, and 4 is much too big, because it”s twice the side-length. I feel like there must somehow be a way to tell that 2.5 is also too small. Otherwise, I don”t see any reason for the College Board to have included the decimal approximations in choice (B) and choice (D), because the College Board only seems to include these approximations when there”s some kind of rough reckoning that can be used to rule out certain choices.
So if you”d like a little mental exercise, see if you can figure out a way to eliminate values of 2.5 or smaller in this question without doing the actual math. I”m pretty sure that will leave you with the fastest possible solution to the question.
(If, like me, you can”t see a way to do that, there”s no real problem—we should still have plenty of time left over from answering most of the other questions as quickly and efficiently as possible.)
Page 586, Question 20
This question offers a classic example of the kinds of information we can glean from a question by thinking of the answer choices from the very beginning.
Most test-takers will try to answer this question by coming up with an algebraic expression on their own and then looking in the answer choices to find a match. That approach can work if you do it perfectly, but it”s very challenging for some people.
What I would recommend instead is to think about the similarities and differences in the answer choices and how they might be relevant to the concepts in the question.
If we look at the elements in the answer choices, we see that each choice is a fraction, with either n or 100n on the top, and either n + 75 or 2n + 75 on the bottom (choice (C) also has 100 on the bottom).
So we basically only need to figure out the answers to these questions:
1. Should 100 be involved in the correct expression? If so, in the numerator or in the denominator?
2. Should the denominator contain the expression n + 75 or 2n + 75?
Let”s think about that. As for the issue with 100, we”d want to realize that the question is asking for a percentage but the answer choices are all fractions. Ideally, thinking about the percentages-versus-fractions issue along with the idea of 100 should remind us that we have to multiply fractions by 100 to turn them into percentages (because fractions describe a portion of a single unit, and percentages describe a portion of 100 units). So we should have 100 in the correct expression, and it should be in the numerator because we”re multiplying by it.
Now, should the denominator have n or 2n? For a lot of people, the temptation is to say that 2n doesn”t make any sense, because it doesn”t appear in the text of the question. But there are a couple of clues in the answer choices that should make us re-examine that assumption. For one thing, if 2n were just some pointless, random mistake, we wouldn”t expect to see it repeated across multiple answer choices; instead, we”d expect that other choices would have other random values like 3n or 4n. On top of that, 2n + 75 actually appears more often in the denominator than just n + 75, which would suggest, according to the answer choice patterns we talked about for the SAT Math section, that 2n is actually the correct version. (Just to be clear, there”s no guarantee that 2n is correct just because it shows up more often, but in general the elements that show up more often will tend to be part of the correct expression.)
So we really want to revisit this idea of 2n. Is there any way it could make sense—either as the correct answer, or as an understandable mistake?
Actually, it makes sense as the correct answer when we realize the question is asking us to compare the number of male students to the entire number of students in the whole college. So the number in the denominator needs to reflect both the male and female students together. We know that the number of female students is given by n + 75, and the number of male students is given by n. So the sum of the female and male students will be n + 75 + n, or 2n + 75.
That means (E) must be correct.
(Notice, by the way, that 100 appears in 3 of the 5 answer choices, which strongly suggests it”s part of the right answer. In those 3 appearances, it shows up twice in the numerator, which suggests—but, again, does NOT guarantee—that it ought to be in the numerator in the correct answer.)
Page 595, Question 8
I remember being asked about this question for the first time in a live class I was teaching literally the first weekend after the second edition of the Blue Book came out. I had never seen the question before and for some reason I completely panicked in front of my students (which I almost never do). I had to admit sheepishly that I wasn”t seeing whatever I needed to be seeing, and ask the students to allow me to give them the solution over lunch break when I would have time to think more clearly. (This, by the way, is the only time in my life I ever needed to do that. But sometimes these things happen. As it would turn out, all of my troubles were caused by straying from my normal game plan because I let myself get stressed out. More on that in a moment.)
The difficulty in this question, for most people, arises from the fact that it looks like the small triangle at the top of the figure has a nearly horizontal base. We really want that base to be horizontal, because then it will be parallel to the base of the large triangle, and then c would just be 180 - a - b, like choice (C) says.
Unfortunately, the base of that top triangle just isn”t horizontal, no matter how we look at it, which means (C) can”t be right. And this is where panic mode might start to set in.
When we panic on the SAT Math section, our normal reaction is to try to make things as complicated and advanced as we can, because that kind of thing usually works on math in school. But on the SAT we want to try to have the opposite reaction, actually—we want to try to look at the question in a simpler, more basic way.
On the day that I panicked in front of my students, for some reason I completely abandoned this principle and started writing out extremely complicated algebraic expressions trying to relate the different measurements of the various angles to one another. It was a mess. In general, if you find yourself writing out gigantic algebraic expressions to solve an SAT Math question, you”re probably doing it wrong. At the very least, you”re doing it in a much, much more complicated way than necessary.
So anyhow, when I looked back at the question a second time over my lunch break, I immediately saw the solution—and it was much, much easier than anything I had previously thought of. In fact, it took about 5 seconds to do, and didn”t even involve picking up a pencil.
The fast solution comes from noticing that the 3 small triangles with angle measurements marked in them all combine to form a quadrilateral, and the angle measurements in a quadrilateral add up to 360o. So we can find the value of c by beginning with 360o and subtracting out all the other angle measurements, giving us 360 - 2a - 3b, which is what (E) says.
There”s a very big lesson in the mistake I made on this question when I first saw it—it”s one I apparently needed to be reminded of at the time, and one you need to learn now if you want to do well on the SAT Math section. Remember that questions on this test can be answered quickly and usually pretty simply. Remember that having to write out long algebraic expressions or go through 15 steps to get an answer means you”re not looking at the question in the best way. Remember to look at the answer choices (I would have seen that 360 appears twice in the choices, which should have been a dead giveaway that a 4-sided figure might be involved, since there are clearly no circles in the question). Remember, above all, that this is the SAT, and the typical school approaches to math just don”t work here most of the time.
Page 598, Question 18
At first glance, this question might look like a normal permutation question. But when we read closely, we realize that this question has a unique aspect that makes it different from typical permutation questions. In this question, one of the cards is forbidden to appear in two of the five positions.
So we can”t use a standard factorial calculation here, because the factorial wouldn”t take into account the limitations on the gray card. The factorial would tell us the total number of arrangements if every card could appear in every position.
But we can use the underlying logic that makes the factorial work, and modify how we apply it so that it fits the current situation. I can think of two ways to do that.
For the first way, we”ll start with the idea that we”re going to figure out the number of cards that can appear in each position, and then we”ll multiply all the possibilities for each position together so we arrive at the total number of possible outcomes for all five positions together.
Since we have to make sure we don”t end up with the gray card last, I”d figure out the number of possibilities for the end positions first, and then the number of possibilities for the middle positions.
For the first end position, we can put any one of 4 cards (any of the non-gray cards).
For the second end position, we can put any one of 3 cards (there are 3 non-gray cards left after we use the first one for the first end position).
For the first non-end position, we can put any one of 3 cards (there are 2 non-gray cards left, plus the possibility of the gray card).
For the second non-end position, we can put any one of 2 cards.
Finally, for the last non-end position, there will only be one card remaining.
So multiplying the number of possibilities at each position gives us 4 * 3 * 2 * 1 * 3, or 72.
Another way to go would be to figure out the number of possible arrangements if the gray card could go anywhere, and then subtract out the possibilities with the gray card at either end.
If we didn't care about where the gray card went, there would be 120 possible arrangements of the cards, because there would be 5 possible cards for the first slot, 4 for the second slot, 3 for the third, 2 for the fourth, and 1 for the fifth, and 5 * 4 * 3 * 2 * 1 = 120.
Now we have to subtract out the situations in which the gray card is at the first position or the last one. Since there are 5 cards, it stands to reason that each card is in each of the five positions for 1/5 of the 120 arrangements. We don't want to count the 1/5 of 120 where the gray card is first, and we don't want to count the 1/5 of that 120 where it's last. So we want 120 - 2/5(120), or 120 – 2(24), or 120 – 48, or 72.
Either of these approaches is perfectly valid, and there are probably other ways you could choose to tackle this question as well. I would probably advise against trying to list out all of the possible outcomes here, for two reasons. First of all, there are too many things involved, so it would probably take too long. Secondly, there are no answer choices, so if you miscounted by even one possible arrangement you”d end up with the wrong answer (if there were answer choices and you ended up differing from one of the choices by only one, you could probably assume that you had miscounted, but without answer choices that will be harder to catch).
This question is one more great example of why we don”t really need to use formulas very often on the SAT. There”s no formulaic way to attack this question that the average high school student will be familiar with in advance; instead, we have to think about the bizarre situation it presents us with, and then figure out a way to respond to that.
Page 642, Question 17
Students ask about this question all the time. It”s probably one of the most time-consuming questions in the entire Blue Book.
For this one, we have to realize that we need the equation for linel, so we can plug t and t+1 in for x and y, and then solve.
In order to figure out the equation, we need two things: the y-intercept, and the slope.
It may seem hard to figure out the y-intercept for linel, because we don”t seem to have enough information. But, as always, we need to remember that the SAT gives us enough information to answer questions, and we need to remember that careful reading is very important. We actually can figure out the y-intercept for linel, because we're told that the line goes through the origin, which means that its y-intercept is 0. So now we just need the slope.
We can find the slope because it must be the negative reciprocal of the slope of the other line, since the two lines are perpendicular. Since the other line has a slope of -4,linel has a slope of 1/4.
Now we know that linel has the equation y = (1/4)x, so we just plug in t and t + 1 and solve:
t + 1 = (1/4)t (original equation with t and (t + 1) subbed for x and y)
4t + 4 = t (multiply both sides by 4)
3t = -4 (combine like terms)
t = -4/3 (isolate t)
So (A) is correct.
Looking at the other answer choices, I would be a little worried because it looks like the choices are trying to distract me from choice (E)—choice (E) is the only one with both its reciprocal and its opposite in the answer choices. So I would double-check my work to make sure that I hadn”t accidentally switched my signs or something.
Page 643, Question 20
Test-takers miss this question all the time, even though it only involves basic arithmetic. This is just one more example of how important it is to pay attention to details on the SAT, and really make sure we lock down every question we can.
If we”re familiar with the definitions and properties of words like “remainder” and “factor,” we can work this out logically. If we were going to think about it in the abstract, we”d realize that if the remainder is going to be 3, then we know that we”re looking for factors of 12 that aren”t also factors of 13, 14, and 15, because 15 - 12 is 3. The factors of 12 are 1, 2, 3, 4, 6, and 12. But 1, 2, and 3 don't work, because they”re all factors of either 14 or 15, so we're left with 4, 6, and 12, and the answer is that there are three possible values for k.
The more concrete way to do this would be to list all the numbers of from 1 to 15, and then write down the remainders when 15 is divided by each of them:
15/1 = 15 r 0
15/2 = 7 r 1
15/3 = 5 r 0
15 / 4 = 3 r 3
15/5 = 3 r 0
15/6 = 2 r 3
15/7 = 2 r 1
15/8 = 1 r 7
15/9 = 1 r 6
15/10 = 1 r 5
15/11 = 1 r 4
15/12 = 1 r 3
15/13 = 1 r 2
15/14 = 1 r 1
15/15 = 1 r 0
So we can see that there are three numbers that produce a remainder of 3, and they are 4, 6, and 12.
So (C) is correct.
When people get this wrong, it”s either because they”ve forgotten the meaning of the word “remainder,” or because they”ve miscounted the number of things that produce a remainder of 3. Both of these are elementary math mistakes—exactly the kind of thing that you can”t let happen on the SAT Math section.
Page 655, Question 18
Most test-takers will try to apply the distance formula here (or else they”ll fail to remember the distance formula and then just take a guess at the answer based on nothing).
The distance formula would ultimately work here, but I prefer to think in terms of the Pythagorean theorem—and, after all, the distance formula is just one specific application of the Pythagorean theorem anyway.
(The Pythagorean theorem says that, in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the legs: a2 + b2 = c2, where c is the hypotenuse and a and b are the legs. If you forget the Pythagorean theorem, you can always go to the beginning of any SAT Math section and find it in the box of provided formulas.)
Some people would choose to diagram this question. Let”s work it out mathematically first, and then we”ll see what a diagram might look like.
If we”re thinking in terms of the Pythagorean theorem, the distance between the two points will be the hypotenuse in the theorem, and the horizontal and vertical changes between the two points will be the legs in the theorem.
We know that the hypotenuse, or the distance, is 17.
We know that the separation in the y axis is 15, because point B has a y value of 18 and point A has a y value of 3, and 18 - 3 is 15. We”re looking for one possible value of x, so we need to know how big the separation in the x-axis must be in order for it to be true that a2 + b2 = c2 when a is 15 and c is 17. So let”s figure it out. 152 is 225, and 172 is 289. So that gives us this:
225 + b2 = 289 (Pythagorean theorem)
b2 = 64 (combine like terms)
b = 8 or -8 (isolate b)
So we know that the separation in the x-axis must be 8. (Don”t make the mistake of thinking that 8 is the answer to the question! 8 is just the length of the separation in one axis, but the question is asking for an actual coordinate in the x-axis.)
Since the x-axis separation is 8 units and the x-value for B is 10, we know that the x-value for point A must be either 2 or 18. So the answer can be either 2 or 18.
Now let”s take a look at what we might get if we decide to diagram this. First, let”s get a rough idea of where point B is:
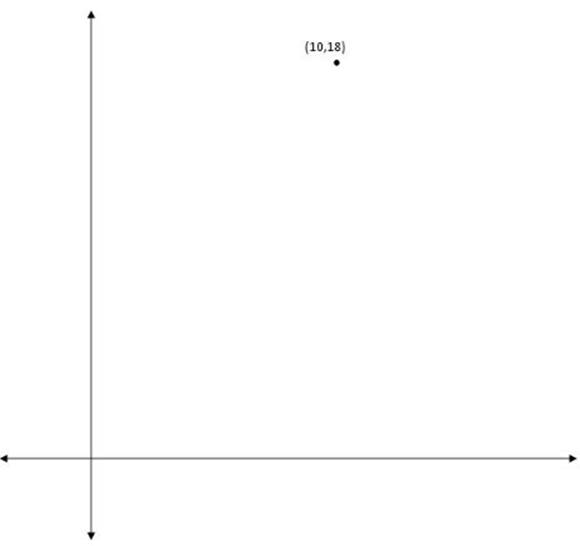
When we try to plot point A, we start to see the difficulty in the question: we have one coordinate for A, but not
the other, so we can”t plot it. All we can do is say that A must lie somewhere on the line of y = 3, because its y-value is 3.
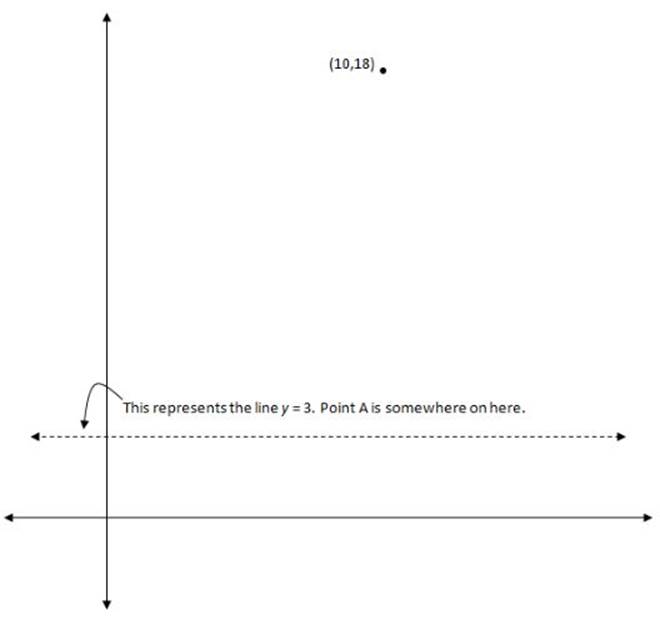
So now the issue is that A is 17 units away from B, and A is also somewhere on the dashed line in the diagram. So we have to figure out exactly where A can go. At this point, I would draw a circle (or part of a circle) showing the points that are 17 units away from B. A must be on a point where this circle intersects the line y = 3 above.
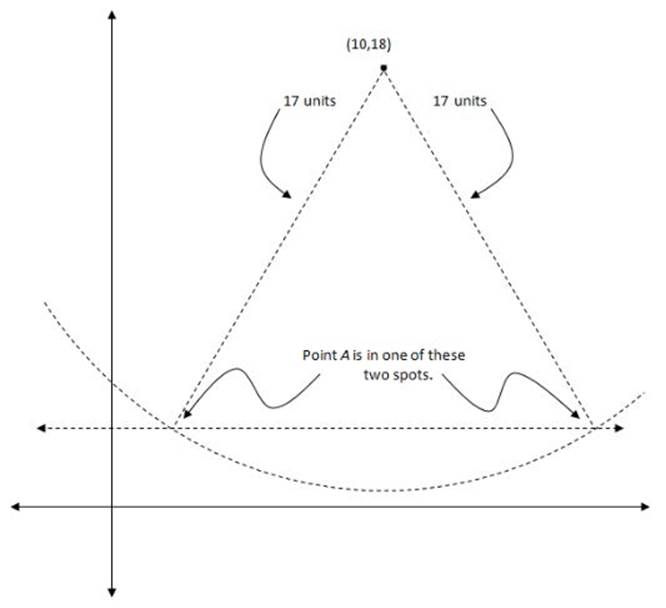
Now, all we have to do is figure out the x-value of either one of those two spots where A could be. For this, we”ll want to use the Pythagorean theorem. The separation between the y-values of the two points will be one leg in our right triangle. The separation between the x-values of the two points will be the other leg. And the hypotenuse will be the 17-unit straight-line distance between the two points:
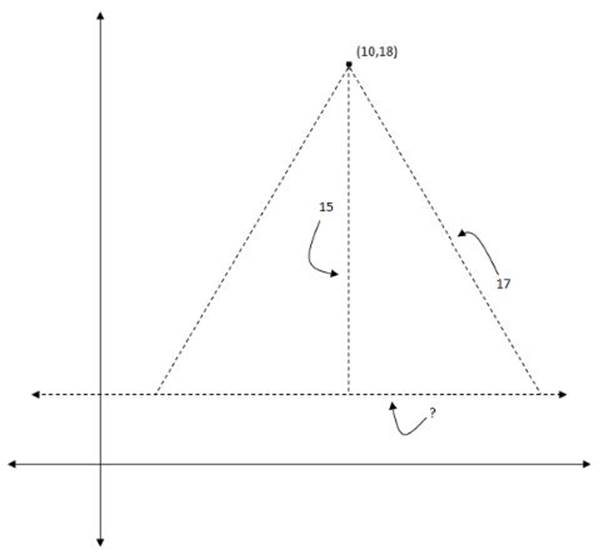
From here, we can apply the Pythagorean theorem as we did in the other approach, and realize that the horizontal leg in the triangle must have a length of 8 units, which means that the x-value for point A must be either 2 or 18.
Again, we could have done this in a more formal way by using the distance formula:
d = √((y2 - y1)2 + (x2 - x1)2 )
But, in general, I advise you to avoid formulaic thinking on the SAT, because there are so many instances on the average SAT Math section in which a formula might seem appropriate when it actually isn”t. And even when a formula might work on a particular question, it”s almost always going to take more time and energy than a non-formulaic approach, and it will also typically increase the likelihood of a mistake on your part.
Also, in the case of the distance formula, I find that it”s much easier for most people to remember and apply the Pythagorean theorem than to recall every detail of the distance formula correctly. And since the SAT doesn”t care how you arrive at the answer, I generally advise people to work in whichever way seems easiest at the time.
Page 671, Question 15
For this question, the key thing is understanding what the idea of modeling the data means. We're looking for the line that provides the best match to the general trend of the data points. Since the data doesn't increase or decrease as you move from left to right, the only thing that works is (A).
Note that (B), (C), and (D) would all have to go through the point (0,0), which clearly isn”t appropriate here. Lastly, (E) would be increasing as it went to the right—it would pass through (0,44) and (5,49). We don”t want that kind of positive slope because if we look at the plotted points we can see that the values are not increasing overall as we move left-to-right. The highest value is in the second trial, and one of the lowest values is in the 5th.
This is one more example of a question that”s fairly easy if we read carefully and pay attention, but that many test-takers will miss anyway.
Page 671, Question 16
As with many SAT Math questions, there are a lot of ways to go about this one. The easiest approach, I think, is to convert either 12L or 10L to W, and then figure out the number of L x W rectangles, since that”s what the question asks for.
The only way to convert L to W is to notice that 2L = 3W, which we know because 2L and 3W both correspond to the height of the big rectangle in the diagram.
If 2L is 3W, then 12L is 18W.
That means the area being covered can be expressed as 18W x 10L, or 180LW. Since LW is the size of each tile, that means we would need 180 tiles. So the answer is (E).
Notice that one of the wrong answers, (B), is 1/5 of the right answer. This makes sense, because a lot of people might accidentally determine the number of times that the big rectangle in the diagram could fit into the 12L x 10W region.
Page 703, Question 14
Most students I”ve worked with on this question have ultimately arrived at the right answer, but they often don”t see the easiest way to get there.
Most of them try to figure out the median slope by determining the slope of every single line segment in the question, and then trying to arrange them from least to greatest (which they usually do by converting them all to a common denominator). It”s quite time-consuming.
The much easier thing is to pay attention to the diagram and to think about what the concept of slope means in the first place. The slope of a line is a measurement of how slanted it is, in a manner of speaking. So the line segment with the median slope will be the one whose “slantiness” puts it in the middle of all the other segments.
In other words, we can tell that line segment OC is the one with the median slope just by looking at the diagram. Now all we have to do is determine the slope of OC, and we”re done. Since OC starts at the origin and point C is at (4,3), that means it goes up 3 units and over 4, for a slope of 3/4. So (C) is right.
Notice that all the other answer choices are the slopes of the line segments, which allows test-takers to make all kinds of mistakes and still find a wrong answer that they”ll like. Remember to pay attention to details!
Page 705, Question 19
This question is one more excellent example of how we always have to be ready to apply basic math ideas in non-traditional ways. In this case, we”re asked to find equivalent proportions even though every proportion involves 4 variables and we”re never told the values of any of those variables. How is that possible?
In situations like this, it”s often helpful to fall back on the idea of trying to identify concepts related to the things that appear in the question. In this case, pretty much the only usable concept we have in front of us is the idea of cross-multiplying.
As it turns out, if we cross-multiply each answer choice, we”ll see that choice (A) gives us ac = bf, but all the other choices give us af = bc.
That means choice (A) is the one that”s not equivalent to the others.
So, in the end, we never learned the values of any of these variables, and we never did anything more complicated than cross-multiplying to answer the question. Many, many test-takers must have missed this question, but when I talk to students who”ve missed it I”ve never met one who didn”t know what cross-multiplying was. Remember that the challenge on the SAT Math section is to identify the basic concepts that will solve the problem.
Page 705, Question 20
Remember that these questions with roman numerals are typically going to be based on some kind of abstract property of the concepts in the question. If we can figure out what that property is, answering the question will usually be pretty straightforward.
For instance, the question tells us that roman numeral I will work out to ab - b. So we have to ask ourselves if there are any conditions in which that might be equal to zero.
That should raise the question, “when can subtracting one thing from another give us zero?”
The answer is that subtracting one value from another can only result in zero when the two values were equal to start with. This is a property of zero.
So ab - b can only equal zero if ab and b are equal to each other.
And that leads to another question: when can ab and b be equal? When can we multiply something by a and have it equal our original starting value, in this case b?
We can only multiply something by a without changing its value if a equals 1. This is a special property of the number 1.
So, in the end, ab - b can only equal zero when a equals 1, because if a is 1 then the expression ab - b is the same as the expression b - b, which must be zero.
So that means that the expressions in each of the other answer choices can only come out to be zero if the part of the expression before the box can possibly equal 1, like a could in roman numeral I.
For roman numeral III, then, it”s pretty clear that the value can work out to be zero if we just make a be 1 again.
But what about roman numeral II?
The (a + b) expression at the beginning of roman numeral II could work out to be 1 if a and b could be fractions or even if one could be negative. But the question tells us that a and b must be positive integers, which means the lowest possible value for a + b is 2. And that can”t work.
So the correct answer here is (E): only roman numerals I and III can work.
Notice that this question has really no resemblance to anything that ever happens in the average math class in school. Notice that with this solution we never really needed a calculator, or even a pencil. Notice, also, that there”s no other question in the entire book that calls for the same specific approach to that this one calls for. In other words, the lesson to learn from this question is NOT the idea of specifically attacking roman numeral questions by looking to see what kinds of subtraction can result in zero, because you”ll probably never see a question that tests that concept in this exact way again. Instead, the lesson to take away from this is, as always, that we need to practice thinking about SAT Math questions in terms of basic principles, definitions, and properties. We need to read everything carefully. And we have to learn to be flexible in our thinking in the way that the SAT Math section rewards over and over again.
Page 714, Question 8
This question is a marvelous example of how important it is to be aware of the limitations of what the SAT Math section can ask you. Most people try to approach this question by taking the 6th root of both sides of the equation, but, as trained test-takers, we need to know that the SAT can never ask us to take any root besides the square root. So taking the 6th root isn”t going to be the easiest way to go here (and anyway, the 6th root of 432 is an irrational number).
So now what?
Well, as is often the case, there are two basic ways to go here. We can try a kind of backsolving, brute-force sort of approach, or we can try using algebraic principles. The first kind of approach requires less familiarity with math but will be a bit more time-consuming for most people, since it”s basically just trying a whole bunch of hit-or-miss combinations of a and b values. The second approach will go a little faster but will be harder for most test-takers to think of or pull off.
If we were going to do the first approach (the hit-or-miss approach), we”d start out by listing all the factors for the quantities in the answer choices. Notice, by the way, that the choices have a lot of factors in common, since they”re all multiples of 6. That would suggest that concentrating on numbers like 2, 3, and 6 might not be a bad way to start.
Anyhow, to start working through our options, we”d take an answer choice like (A), figure out its factors (they”re 1, 2, 3, and 6), and then get out our calculators and start plugging in combinations of those factors for a and b in the original expression to see if we could come up with a value of 432.
This will be made more challenging and time-consuming by the fact that, to be really thorough, you have to try each factor for a and again for b, since they aren”t treated the same in the expression.
But it”s made a little easier by the fact that some combinations of factors will prove to be too small or too large, which might help you adjust your guessing and hit on the right answer more quickly. A lot of people who try these kinds of backwards solutions like to start with (C), since it”s the value in the middle, see how that goes, and then adjust up or down. In general I think that”s a fine approach, but in this case it might result in more work because the larger numbers probably also have more pairs of factors to work with. So it”s a toss-up, in my opinion—start where you like.
The second approach, as I mentioned, is a bit more mathematical, and is the one I would probably employ (not that that matters).
I would start out by realizing that I can simplify the expression on the left-hand side of the equation, so that the whole equation reads like this:
a3b2 = 432
Now that”s starting to look like something we might have seen at some point in algebra class—it”s starting to look a bit like a prime factorization, with a and b being the possible factors of 432.
So at this point, I”d break down 432 into its prime factors. I”d do this by using what my algebra teacher, Mrs. Turner, used to call a “factor tree.” They look something like this:
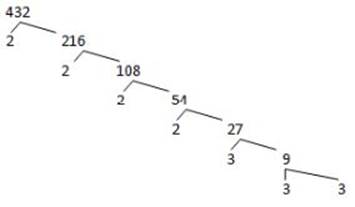
From this, we can see that the prime factorization of 432 is 24 * 33.
That”s almost what we”re looking for, except for one small problem: 432 is the same thing as 24 * 33, but we”re looking to express it as a3b2. It looks like the a can match up with the 3 in our factorization, because they”re both cubed, but how do we get b2 to match up with 24? We”ll have to realize that 24 is 16, and 16 is 42.
That means that a3b2 is 432 when a is 3 and b is 4. And that, in turn, means ab is 12, so (B) is correct.
As far as our answer choices are concerned, we see that we have a series of multiples of 6. In this situation we”d expect the right answer not to be a value on either end of the series—maybe that”s not a ton of help here, but at least it doesn”t suggest we”re wrong.
Page 717, Question 17
A lot of people get nervous when they see this question, because they”ve never encountered a shape like the one in the diagram. But as trained test-takers, we have to remember that we”re always going to see new stuff on the SAT, and our job is to figure out how to apply basic math knowledge in these new situations.
In this case, as in many other questions, it”s just a matter of reading carefully. The only line segments that will be on edges are the ones to the vertex directly to the left of V, directly to the right of V, and directly underneath V. That means that the lines to the other 8 vertices aren't on the edges of the figure.
Like many of the SAT Math questions that most test-takers struggle with, this question involves no formula and no chance to use a calculator. It”s just a matter of reading carefully and then subtracting 3 from 11 and arriving at 8 as the answer.
Page 717, Question 18
This question challenges many test-takers, usually because the drawing looks so complicated. But if we think carefully and work through the question, we”ll find that it only relies on basic math at its core, just like all SAT Math questions.
The question asks us to find p. Since the only mention of p in the whole question is in the equation y = px3, that”s pretty much where we”ll have to start.
The only way we can get p out of y = px3 is to know the values for y and x. So that means we need to be able to identify the x and y values for some point on the graph of the function.
Apart from (0,0), which would be useless for us here, the only clear points that the function passes through are the ones labeled A and C.
Since C has x and y values that are positive, let”s focus there. We know that C is at (1/2,c). So now we need to figure out the dimensions of triangle ABCD.
Since we know the area of ABCD is 4, and the diagram shows its width is 1 unit based on the x-coordinates, then we know that ABCD has a height of 4.
This means that point C is at (1/2 , 2). Now we just plug those x and y values into y = px3:
2 = p(1/2)3 (plug in 1/2 for x and 2 for y)
2 = p(1/8) (simplify on the right)
16 = p (isolate p)
This question was a bit more involved than many SAT Math questions. We know to expect that some time near the end of the grid-ins. But the solution still only involved a bizarre combination of basic facts—something else we”ve come to expect from SAT Math questions in general.
The real lesson to take away from this question is the idea of tracing the solution back through the concepts in the question. Here, they asked about p, so we looked in the question for a statement that was relevant to p, then we thought about things that were relevant to that statement, and so on. This general approach will come in handy on other SAT Math questions, even though this particular question will never appear on a real test in the future.
Notice, also, that this question is actually very similar to question 18 on page 530 of the College Board”s Blue Book. I”ll repeat here what I said earlier in the explanation for that question: do not be misled by this coincidence into assuming that the College Board frequently repeats a limited number of question types in each SAT Math section. On the contrary, in the entire Blue Book these two questions are one of the only examples of question material being repeated so closely on the SAT Math section.
Page 732, Question 14
Many students get nervous over this question because they don”t like things that deal with ranges and inequalities, but it”s important to remember that we don”t have to do these questions in ways that we could defend to a math teacher. We just need to find the answer any way we can.
I would start by multiplying the smallest and greatest values of x and y together, and then seeing how those things relate back to the answer choices. The smallest and greatest values of x are 0 and 8, while the smallest and greatest values of y are -1 and 3. So:
0 * -1 = 0
0 * 3 = 0
8 * -1 = -8
8 * 3 = 24
So our range of possible values for xy at least needs to include -8 and 24.
That means (E) is the only choice that works.
If we look at the answer choices, it”s a good sign that many of the choices end in 24. It”s not a great sign that only one choice ends in -8, but we could easily pause to double-check the validity of -8 by realizing that 8 * -1 is, indeed, -8.
In fact, from a certain way of looking at it, once we”re positive -8 is a valid option we can actually stop doing any further work, because only one choice includes it.
(Now, if you”re a math teacher or a strong math student you might be shaking your head at my approach here, which is quite informal. In fact, you might shake your head at a lot of what we do in the Black Book because of its informality. But my goal isn”t to show my students how to attack SAT Math questions formally, because formal solutions to SAT Math questions are typically slower and more difficult than the simple, direct approaches I want my students to follow. I”m not teaching math in this book; I”m teaching how to answer SAT Math questions. The distinction is important.)
Page 770, Question 8
Many test-takers miss this question, even though it involves nothing more than careful reading and basic arithmetic.
The question says that the new average is equal to the median number of siblings per student. That means we need to figure out what the median number of siblings is, and then figure out how to make the new average number of siblings equal to that median number.
So let”s start by figuring out the median number of siblings.
We see there are 3 students with 0 siblings, 6 students with 1 sibling each, 2 students with 2 siblings each, and 1 student with 3 siblings. So if we arrange the number of siblings for each student in a row from least to greatest, we”ll get this:
0,0,0,1,1,1,1,1,1,2,2,3
So the median number of siblings is 1, because the numbers in the middle of that series are both 1.
So when the new kid joins the class, the average number of siblings that everyone has is going to equal this median number of 1. When the new kid joins the class, there will be 13 total students in the class, which means the total number of siblings for all the kids in the class must also be 13 (because 13/13 is 1).
So now we add up the numbers of siblings of existing students, so we can see how far we are from a total of 13 students:
0 + 0 + 0 + 1 + 1 + 1 + 1 + 1 + 1 + 2 + 2 + 3 = 13
So actually, it turns out that the 12 students already in the class have a total of 13 siblings already, which means that the 13th student needs to have zero siblings in order for the average number of siblings in the class to be 1.
That means (A) is correct.
Now let”s review the math ideas that were necessary to answer this question. We had to know how to read a relatively simple table. We had to know what the words “median” and “average” meant. We had to arrange a lot of single-digit numbers from least to greatest. We had to figure out that a lot of single-digit numbers added up to 13. We had to know that 13/13 is 1. And we had to know that 13 + 0 is 13.
None of that would probably qualify as advanced mathematical knowledge at your school, but test-takers miss this question very, very often. We should ask ourselves why that is, so we can make sure we don”t make their mistakes.
In my experience, people who miss this question (or just give up on it in the first place) do so because they don”t understand what it”s asking when they read it. This is why I often say that critical reading skills are the most important thing on the entire SAT. And it”s because of the great number of questions like this—questions that present bizarre combinations of simple math ideas—that test-takers who try to prepare for the SAT by learning advanced math usually don”t see any improvement.
Page 773, Question 17
For this question, as for many abstract questions on the SAT Math section, there are two ways to go: we can come up with concrete values for the variables described in the question and run a test, or we can think about the question in the abstract. The concrete approach tends to take more time but will often feel more comfortable, while the abstract approach is faster but will be harder for many test-takers to manage.
In this explanation, I”ll start with a concrete example and then show the abstract one. You could use either on the test, of course, without bothering to think about the other.
Let”s assume that p is 3, r is 5, and s is 7, as those are three different prime numbers greater than 2, like the question asks us for.
In that case, n is 3 * 5 * 7, or 105.
Now let”s figure out what the factors of n are:
1, 3, 5, 7, 15, 21, 35, 105
There are 8 of them, so the answer to the question is 8.
Now, if we wanted to think about this in the abstract, we”d note that since n is the same as prs, and since p, r, and s don”t have any other factors besides 1 (since they”re prime), then the factors of prs will include every possible combination of p, r, and s, like this:
p, r, s, pr, ps, rs, prs
. . . plus, of course, 1.
That also makes for a total of 8 factors.
(Notice that the concrete example we did follows our abstract thinking perfectly if we substitute 3 for p, 5 for r, and 7 for s.)
Page 785, Question 2
People often miss this question, even though it”s fairly early in the section and doesn”t really involve any math. When they miss it, it”s usually as a result of not having read it carefully. Most people choose (A) because the figure in that choice has a line of symmetry, and they”re rushing through the question. They don”t notice that 3 other choices also have a line of symmetry, which might help them realize their mistake.
If we read carefully and realize we”re looking for a figure with 2 lines of symmetry, then we realize that (D) has one line of symmetry going vertically straight down its center and another line going horizontally straight through its center.
It”s a real waste to miss a question like this! Make sure you pay proper attention to every single question on the entire test. Even the so-called “easy” ones can trip you up if you rush.
Page 789, Question 18
This is one of those questions in which knowing the unwritten rules of the SAT Math section comes in especially handy.
Most people who try to answer this question will either use some version of a summation formula or they”ll actually try to add up every integer starting from -22 until they hit a running total of 72.
Either approach could conceivably work, but neither is very fast, nor very easy.
Instead, we want to remember that there must be some way to do this question in under 30 seconds relying only on some combination of basic arithmetic, algebra, and/or geometry.
One thing that would jump out at me right away is that we”re looking for a positive sum, but we”re starting by adding up some negative numbers in the beginning of our series. That means we”ll have to add quite a few numbers before our running total becomes positive, because at the beginning of our series (-22, -21, -20, . . .), the running total will just become increasingly negative.
So wait a second . . . when does the running total start to creep towards a positive balance?
Well, that won”t happen until we start adding in some positive numbers, of course. So our series will have to go past zero, for sure.
And when it passes zero, for a while, each positive number added to the running total will only serve to erase one of the negative numbers already added to it. Positive 1 undoes -1, for instance, and positive 2 undoes -2, and so on.
If we think about it, then, we”ll see that every number from -22 to positive 22, added together, gives a sum of zero, because every positive number in the series is outweighed by a negative number and vice-versa.
So all the numbers from -22 to positive 22 add up to zero. Then what happens?
We add in positive 23, positive 24, and positive 25, and we”ve reached our grand total of 72.
That means that all the numbers from -22 to positive 25 add up to positive 72. So (B) is the answer.
Notice some of the wrong answers here. (C) is the sum of the two numbers in the original question, while (E) is the difference. (A) is the first positive number that produces a positive value when added to the running total, so some test-takers will probably accidentally choose it because they”ve realized it marks the beginning of the positive running total without remembering what the question was actually asking.
Page 799, Question 14
People often get frustrated by this question because they can”t figure out the values of b and c. In school math classes, we”re often programmed to find the values for every variable in a question, but on the SAT Math section we often have to let go of that. Sometimes there”s not enough information in a question to figure out the value of every variable, but the question can still be answered anyway. One of the clearest signs of that situation is when the question involves multiple variables but doesn”t actually ask you for each one of their values.
For questions about function graphs, I often like to look at the intercepts. In this case, we know that c is positive, so the y-intercept must also be positive, because the y-intercept is what we get when x = 0.
Only (E) has a graph with a positive y-intercept, so only (E) works.
Page 800, Question 15
I often resist the idea of identifying “types” of math questions on the SAT Math section, because I want you to realize that you”ll basically have to figure out stuff you”ve never seen before when you take the SAT. But if there were going to be a type of question that I might specifically train somebody for, it would be the kind of thing described in this question. (By the way, this comes up less than once per test in the College Board”s Blue Book. The odds that it will ever come up for you on a real test are less than 50%. And, even if it does come up, it”ll probably only count for one question. These are the kinds of reasons why I generally avoid thinking in terms of question types.)
Anyway, for these questions that ask you about the distance from one point of a 3-dimensional figure to another point, you basically have to apply the Pythagorean theorem twice.
Let's label the corner underneath point B as point Q, and let”s label the corner to the right of point A as point T.
So then triangle ATQ has legs of 1 and 2 units, which means that AQ has a distance of √5.
So now we can use AQ, which was the hypotenuse of ATQ, as a leg in the triangle ABQ. Using the Pythagorean theorem again, we get this:
AB2 = √52+ 12
AB2 = 5+ 1
AB2 = 6
AB = √6
So the answer is (D).
Note that one of the wrong answer choices is √5, for people who forget to finish the question.
Page 800, Question 16
This is a question with a made-up function. For these kinds of things, it”s always very important to read and follow directions very carefully.
In this case, people often fail to realize that the right-hand side of the equation should be
(a-2)2 - (a -2). We have to apply the oval function to the whole expression inside the oval, and the whole expression inside the second oval is (a - 2).
Once we do that correctly, all that remains is to solve:
a2 - a = (a-2)2 - (a -2) (substitute the starting values from the question)
a2 - a = (a2 - 4a + 4) - a +2 (FOIL the expression on the right)
a2 - a = a2 - 5a + 6 (combine like terms on the right)
- a = - 5a + 6 (subtract a2 from both sides)
0 = - 4a + 6 (combine a terms)
4a = 6 (separate a term from constant)
a = 6/4 (isolate a)
a = 3/2 (simplify)
So (C) is correct.
As we might expect, one of the wrong answers is twice as much as the right answer. The other wrong answers seem to reflect what we might have ended up with if we had handled the algebra incorrectly.
By the way, another approach to this question, which would probably take longer but would avoid so much algebra, would be to take each answer choice and plug it in to the original expression until you find one choice that results in a true mathematical statement. But even if you do the question in this way, you still need to make sure you handle the substitution properly by reading the question very carefully.
Page 835, Question 18
To answer this one we have to think about what we're given and what we're asked for. We're given the averages of the two groups and asked for the ratio of their sizes. Note that it's impossible to know the actual number of people in each group--one major clue to this is the fact that the test asks for the ratio.
Many test-takers try to approach this question by figuring out individual values for p and n, but it literally can”t be done. It is possible, however, to figure out the value of p/n.
We'll figure out the ratio by using the definition of the term "average," which tells us that if p students have an average of 70, then the total number of points scored by those p students is 70p.
Similarly, the total number of points scored by the n students is 92n.
Using the definition of average, again, we find that the average of all the n students” scores plus the p students” scores must be (70p + 92n)/(n + p) = 86. Then we solve:
70p + 92n = 86p + 86n (multiply both sides by n + p)
6n = 16p (combine like terms)
6n/16 = p (isolate p)
6/16 = p/n (isolate p/n since the question asks for it)
3/8 = p/n (simplify)
Page 848, Question 6
Many test-takers miss this question because they mistakenly think that a square yard is the same thing as 3 square feet. But a square yard is 9 square feet, because a square yard is 1 yard x 1 yard, or 3 feet x 3 feet, or 9 feet2.
Once we know that, it becomes easier to realize the correct answer is 12 * 18 / 9, or 24.
Another way to approach the situation is to convert the dimensions of the floor to yards right from the beginning, so that we calculate 4 yards by 6 yards, again getting 24 yards2.
So (C) is correct. Note that (A) is there for us in case we divide by 3 one time too many, and (E) is there in case we accidentally find the square footage instead of the square yardage. Things like this are why it”s always so important to read carefully on the SAT Math section.
Page 851, Question 15
This question often frustrates people, but it”s actually not as hard as people often think. The question asks for the shortest distance between the center of the cube and the base of the cube. If we visualize the cube, we'll see that the distance from its center to its base is the same as the distance from the center of one of its sides to the base—or, in other words, if you looked at the cube straight on it would look like this:

where C is the center of the square/cube and the bottom line of the square/cube is the base.
If the volume of the cube is 8, then the sides are all length 2, which means the distance from the center to the base is 1 (because it's half the distance from the base to the top side of the cube). So the answer is (A).
Page 852, Question 18
This question provides one more terrific example of the difficulty that the College Board can manage to infuse into an SAT Math question without actually using any math.
This question throws a lot of people. But, as always, all we really need to do here is follow what the text says, alternately switching the left or the right wire with the center wire. So the pattern goes like this:
step 1: BAC
step 2: BCA
step 3: CBA
step 4: CAB
step 5: ACB
step 6: ABC
So the answer is (D). Notice that it”s possible to end up with the wrong answer of 7 if we accidentally count the “Start” as a step. One more moment when critical reading skills really come in handy on the math part of the SAT.
This is also a great example of an SAT Math question for which no formula exists. There”s no way you could use a calculator on this question; there”s not even any real way you could use basic arithmetic. This question is literally about braiding, but untrained test-takers in advanced calculus classes miss it frequently in practice.
Page 852, Question 19
Like the previous question, this one ends up involving no actual math. All we need to do is think carefully about the definition and properties of the term “median.”
If you double the value of each number or increase each number by 10, you must end up changing the median number (because you either double it or increase it by 10, as the case may be).
In other words, if the 11 numbers are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, then doubling them all makes the median 12 and adding ten makes it 16. The median is the value in the middle--that's the definition of the term. Changing the number that's in the middle of the range of numbers changes the median.
(C) or (D) might also end up affecting the median, if we increase the smallest number by such an amount that it becomes greater than the original median, or if we decrease the largest number by such an amount that it becomes less than the original median.
Only (E) has no possibility of changing the median. Increasing the largest number still causes it to remain the largest number, so the number in the middle of the series can”t change.
Page 861, Question 16
Many students try to use some kind of formula here, but that”s a mistake, of course. For one thing, the SAT can't ask us to find the area of a trapezoid because it doesn't give that formula in the beginning of the math section or in the question itself. So there must be some other way to solve the problem that is easier and more direct.
If you draw out the rectangle and the trapezoid, we'll see that the trapezoid takes up 3/4 of the area of the rectangle, like so (I dashed in some other lines so you can see that ABED takes up 3/4 of ABCD more clearly):
So that means that we can do this:
ABED = 3/4(ABCD)
2/3 = 3/4(ABCD)
8/9 = ABCD
This means that the answer is (C).
Notice that one of the wrong answers is 3/4. This is a good sign for us, because it indicates that we were probably on the right track when we figured out that ABED was 3/4 of ABCD.
Page 888, Question 8
This question is often frustrating for untrained test-takers because it seems at first as though it will be impossible to figure out the product of the slopes if we don”t know the slopes themselves, and the question doesn”t tell us the slopes.
But if we remember the definition of the term “rectangle” and the properties of perpendicular lines in a coordinate plane, then we can realize that the slopes of lines that are perpendicular to one another are opposite reciprocals (like, for instance, 2 and -1/2), so they'll have to multiply together to give us -1.
There are two pairs of perpendicular sides, in a rectangle, so the final product of all of these slopes is 1, because -1 * -1 is 1. (For instance, if the slopes were 2, -1/2, 2, -1/2, they would multiply together to make 1.) So (D) is the right answer.
So, in the final analysis, this question really just involved knowing that rectangles have 2 pairs of perpendicular sides, knowing that perpendicular lines have slopes that are opposite reciprocals, and knowing that -1 * -1 is 1. Each of those facts is pretty basic on its own, but most people who look at this question never realize that those facts are involved in answering it. This is why it”s so important to develop the instincts for taking these questions apart by reading carefully, thinking about definitions and properties, and ignoring formulas and calculators for the most part.
Page 906, Question 12
This question basically hangs on the definition of the term “directly proportional.” We need to know that when n is directly proportional to q, n = kq, where k is some unknown proportional constant that we usually need to figure out.
So, in this case, if y is directly proportional to x2, then y = k(x2).
So let”s substitute and see what happens:
1/8 = k(1/2)2 (plug in the given values for x and y)
1/8 = k(1/4) (simplify on the right)
4(1/8) = k (isolate k)
1/2 = k (simplify)
Now that we know what k equals, we can plug it in with a y value of 9/2, to find our new x:
9/2 = 1/2(x)2 (plug in values for y and k)
9 = x2 (combine like terms)
3 = x (isolate x)
So the answer is (D). Notice that our other answer choices include 9, which is what we”d get if we accidentally solved for x2 instead of x, which is a mistake people often make on this question.
It”s not common for the SAT to test a math concept as obviously as it”s testing direct proportionality in this question—the only wrinkle in this question is the idea of being proportional to x2 instead of x. I think this particular question is so direct because direct proportionality is a concept that many algebra teachers no longer cover for some reason. (This is just a theory on my part, but I think it matches the evidence. Math concepts that are more commonly encountered on the SAT aren”t usually tested this directly.)
At any rate, if you saw this question and realized that you had forgotten (or never been taught) the idea of direct proportionality, it would be a good idea to review it. The odds of it coming up on test day for you are relatively slim, but it”s such a simple concept that it can”t hurt to take a few moments to memorize it.
Page 907, Question 18
For this question, as for most SAT Math questions, we simply need to read carefully and look for ways to apply basic math ideas.
If there are 18 arcs of each length in the circle, and if the circle has a circumference of 45 units, then we can write this:
18(2 + b) = 45
That means that 36 + 18b = 45, which means that 18b = 9, so b = 1/2 unit.
If b is 1/2 unit and there are 45 units in the circumference of the circle, then 45 units corresponds to 360 degrees of arc. This means that each of the 45 units in the circle's circumference accounts for 45/360 degrees, or 8 degrees; since b is 1/2 of a unit, b must be 4 degrees, and the answer is (A).
Notice, as is often the case, that the answer choices represent mistakes that can be easily made. 16 degrees is the arc measurement of the 2-unit arcs, and 20 degrees is the arc measurement of a (2 + b) combination.
Page 908, Question 20
This question, like many questions near the end of an SAT Math section, is actually much easier than it might look. It”s also an especially clear example of a few of the SAT Math rules and patterns from this book, all wrapped into one test item.
One of the first things I”d want to notice is that the diagram isn”t drawn to scale. That means I should think about re-drawing it to scale. To figure out how to do that, I have to look at the text of the question, which mentions that each of the five line segments are congruent (which is just a fancy way to say they”re all the same length). That means that this diagram should show two equilateral triangles that share a side, like this:
The text of the question also includes another piece of information that was left out of the original diagram, which is the existence of line segment AC. So I”ll add that in:
Another fundamental thing that we should pay attention to is the set of answer choices. Notice that they all involve either √3 or √2 (choice (E) actually involves both).
We should ask ourselves what kinds of math concepts are related to the concepts we”ve encountered so far. We know the diagram involves two equilateral triangles, and we know equilateral triangles are 60o-60o-60o triangles. We also know that the answer choices involve √3 and √2; √3 is related to 30o-60o-90o triangles and √2 is related to 45o-45o-90o triangles.
At this point, we”d want to realize that line AC cuts the two 60o-60o-60o triangles in half, creating 4 new triangles, and each of these new triangles is a 30o-60o-90o triangle.
We know that the ratio of the legs of a 30o-60o-90o triangle is 1: √3, with √3 representing the long leg. (This is something we”d want to have memorized, but even if you forget it momentarily you can always look at the given information at the beginning of any SAT Math section).
The question asks for the ratio of AC to BD. AC includes two long legs of 30o-60o-90o triangles, while BD includes two short legs of 30o-60o-90o triangles. That means the ratio is 2√3:2, which is the same thing as √3:1, which is what (B) says, so (B) is correct.
Surveying all the answer choices, we”ll see that most of them start with √3, which is a good sign that starting with √3 is probably the correct option. But more of them end with something related to 2, not 1, so I would double-check myself to make sure that I hadn”t made a mistake in simplifying the ratio.
Page 919, Question 15
Most untrained test-takers will see this question and assume that they need to figure out the actual measurements of each angle in the answer choices, because that kind of solution might seem similar to something we would do in a trigonometry class. But, as trained test-takers, we”d want to realize that it”s possible to figure out which angle is smallest without figuring out their actual measurements—and, anyway, trig isn”t allowed on the SAT, so there has to be another way.
Since the two endpoints of each angle are the same (always X and Y), the farther away the vertex is, the smaller the angle will end up being. Since D is the farthest point from X and Y, XDY is the smallest angle, even if we never figure out its actual measurement. So (D) is the correct answer.
Page 919, Question 16
Most untrained test-takers will try to identify the actual values of x and y, because that”s what we would typically have to do in school if we saw a math question with multiple variables. But on the SAT, we”ll frequently be asked questions in which the variables don”t need to be identified, and this is one of those questions. (One of the major clues that we don”t need to identify the variables is that we weren”t asked to find either variable”s individual value; we were only asked to find the value of a complex expression that involves both variables.)
As always, it”s important to think about the answer choices, and how they relate to the concepts and quantities in the question. Notice that every answer choice has a clear relationship to the quantities 7 and 5 from the question:
(A) is the difference of 7 and 5, so it would make sense as the right answer if x2y - y2x were the same thing as the difference between xy and x-y
(B) is the sum of 7 and 5, so it would make sense if x2y - y2x were the sum of xy and x-y.
(C) is twice the sum or 7 and 5, which also doesn”t make any sense here.
(D) is the product of 7 and 5, so it will be the right answer if x2y - y2x is the same thing as the product of xy and x-y. Which is exactly what it is, so (D) is correct.
(E) is twice the product of 7 and 5.
As I”ve mentioned many times, we really want to get in the habit of thinking of the answer choices as part of the question itself, not as an afterthought. Looking for ways that the choices relate back to the text of the question can really help you increase both your speed and your accuracy. This question is one of the most frequently missed questions in this section (we can tell this from the College Board”s difficulty ranking), but it can literally be answered without even picking up a pencil if we notice what”s going on in the answer choices. This question ultimately boils down to paying attention, knowing what 7 * 5 is, and knowing how to multiply simple expressions in algebra.
Page 953, Question 17
This is a grid-in question that asks us to find “one possible value of the slope” of a line that intersects line segment AB. Remember that when a question like this asks us to find “one possible value,” then there must be more than one value possible—whenever a question refers to the possibility of multiple values, there are multiple values.
In this case, any slope value of any line whatsoever that intersects AB will be fine. If a line (8,3) hits point A exactly, then a line through (9,3) must intersect AB. The line through (9,3) will have a slope of 3/9, or 1/3. So that”s one possible value.
Another way might be to try to cut AB in half. To do that, we could imagine a line through (8,1.5), or through (16,3) (that would be the same line, determined at two different, collinear, points). Either one would create a line with a slope of 3/16.
Yet another way to create a valid answer might be to realize that a line with a slope just barely over horizontal would have to intersect AB since point B lies on the x-axis. So we could pick a slope of 1/10 or .001 or something.
Any of these approaches could work, as could a wide variety of others.
Page 969, Question 16
I once saw a YouTube video of a guy who explained how to attack this question in the most complicated way I could possibly imagine. He began by identifying the curve in the graph as a parabola, and then tried to figure out what the equation for the parabola would be (after trying to figure out the coordinates of various points on the parabola, like the vertex, the intercepts, and so on). Once he had the equation of the parabola worked out, he set it equal to 0, solved it, and then found his answer.
It worked, of course, but it created a ridiculous amount of extra work for no reason—and let”s not even mention the extra opportunities for error it created by drawing the solution out unnecessarily.
Unfortunately, that kind of approach is what most test-takers would try on this question, because they”re programmed to answer questions on the SAT Math section the same way they would answer questions in school.
There”s a much easier way to approach this question, which relies on simply understanding the properties and definitions of concepts relating to the graphs of functions.
We should recognize that the places where h(a) = 0 will be the places where the graph of h(a) crosses the x-axis.
We should also recognize that the graph is drawn to scale, which means we can eyeball it relative to the provided values and figure out where the graph crosses the axis from there.
If we look at the answer choices, we”ll see that (A) must be correct, because where x = -1 on the given graph, we find h(a) crossing the x-axis.
Some students are tempted to choose 4 as the answer to this question, because it kind of looks like the right-hand x-intercept of the graph might be at x = 4. But if you look carefully, you”ll see it”s at a position much closer to x = 5. Remember how important it is to pay attention to details!
If we read carefully, look at the graph carefully, and remember to think in terms of things like intercepts, we can answer this question in about 10 seconds, without even picking up a pencil.
Page 981, Question 15
A lot of test-takers drop the ball on this question because they don”t look for the ways to simplify the algebraic expressions involved, or they try to assign values to n and k without making sure that those values satisfy the original requirements of the given equation.
I would start off by simplifying the expression on the left-hand side of the equation, dividing by n/n and “eliminating” an n from the top of first fraction and the bottom of the second fraction. Then it”s a little easier to see that the whole thing could be combined to this:
n/(n2 - 1)
(Notice that (n - 1) can be multiplied by (n + 1) to create the difference of squares (n2 - 1). This is something we”d want to be able to do in our heads, without needing to foil it out manually.)
So now our equation looks like this:
n/(n2 - 1) = 5/k
This means that n corresponds to 5, and (n2 - 1) corresponds to k.
If n is 5, then (n2 - 1) is 24, so the answer is (C).
In our wrong answers, we see the value of n, which helps reassure us that we attacked the question correctly, because it suggests that the College Board is hoping some test-takers will correctly realize that n is 5 but then forget the question was asking for k. We also see a series that goes 24, 25, 26, which might seem odd at first, because normally we”d expect the right answer to be in the middle of a series like that. But there”s a certain logic to it here, because in order to arrive at 24 we have to square 5 and subtract 1; in this case, the wrong answers reflect squaring 5 and adding1, and squaring 5 while forgetting to add or subtract. We can see there”s a certain symmetry the College Board is going for here, in trying to give test-takers a variety of ways to mess this question up. And that can reassure us that squaring 5 and then subtracting 1 was, indeed, the right way to go.
Conclusion
We”ve just looked at a whole bunch of SAT Math questions, and we never really broke a sweat! We did this by sticking to our simple process, and by looking for quick and easy answers. As we saw, the hardest part of each problem was the setup. The actual calculations didn”t present much of a problem, as long as we had our basic concepts in order.
On the next page, you”ll see a brief, one-page summary of the main ideas to keep in mind on the SAT Math section. After that, we”ll dive into the SAT Writing section. You”ll see that the Writing section, like the SAT Math section, is a lot easier to attack if you”re familiar with a core set of basic principles.
Video Demonstrations
If you”d like to see videos of some sample solutions like the ones in this book, please visit http://www.SATprepVideos.com. A selection of free videos is available for readers of this book.