SAT 2016
CHAPTER 2
DIAGNOSTIC SAT
DIAGNOSTIC SAT ANSWER KEY
Section 1: Reading
1. C
2. A
3. C
4. B
5. D
6. C
7. D
8. A
9. B
10. D
11. B
12. C
13. C
14. D
15. A
16. D
17. B
18. D
19. C
20. B
21. B
22. C
23. D
24. D
25. A
26. A
27. C
28. C
29. C
30. B
31. A
32. B
33. C
34. C
35. A
36. A
37. B
38. B
39. B
40. B
41. A
42. D
43. C
44. B
45. D
46. A
47. A
48. D
49. D
50. C
51. B
52. D
Total Reading Points (Section 1)
Section 2: Writing and Language
1. B
2. C
3. C
4. A
5. B
6. C
7. A
8. D
9. A
10. D
11. D
12. C
13. B
14. D
15. A
16. B
17. C
18. D
19. C
20. D
21. B
22. A
23. D
24. C
25. A
26. D
27. C
28. B
29. C
30. D
31. A
32. C
33. B
34. B
35. A
36. B
37. D
38. C
39. C
40. D
41. B
42. B
43. D
44. B
Total Writing and Language Points (Section 2)
Section 3: Math (No calculator)
1. B
2. D
3. B
4. A
5. C
6. D
7. A
8. B
9. D
10. C
11. A
12. B
13. C
14. B
15. B
-------
16. 30
17. 25/7 or 3.57
18. 35
19. 1.2
20. 2.4
Total Math Points (Section 3)
Section 4: Math (Calculator)
1. D
2. C
3. D
4. B
5. D
6. C
7. B
8. A
9. B
10. C
11. B
12. D
13. A
14. B
15. B
16. B
17. C
18. C
19. C
20. B
21. A
22. A
23. D
24. C
25. A
26. D
27. D
28. B
29. A
30. B
-------
31. 1/5 or 0.2
32. 169
33. 112
34. 16
35. 1.4
36. 115
37. 6.8
38. 25
Total Math Points (Section 4)
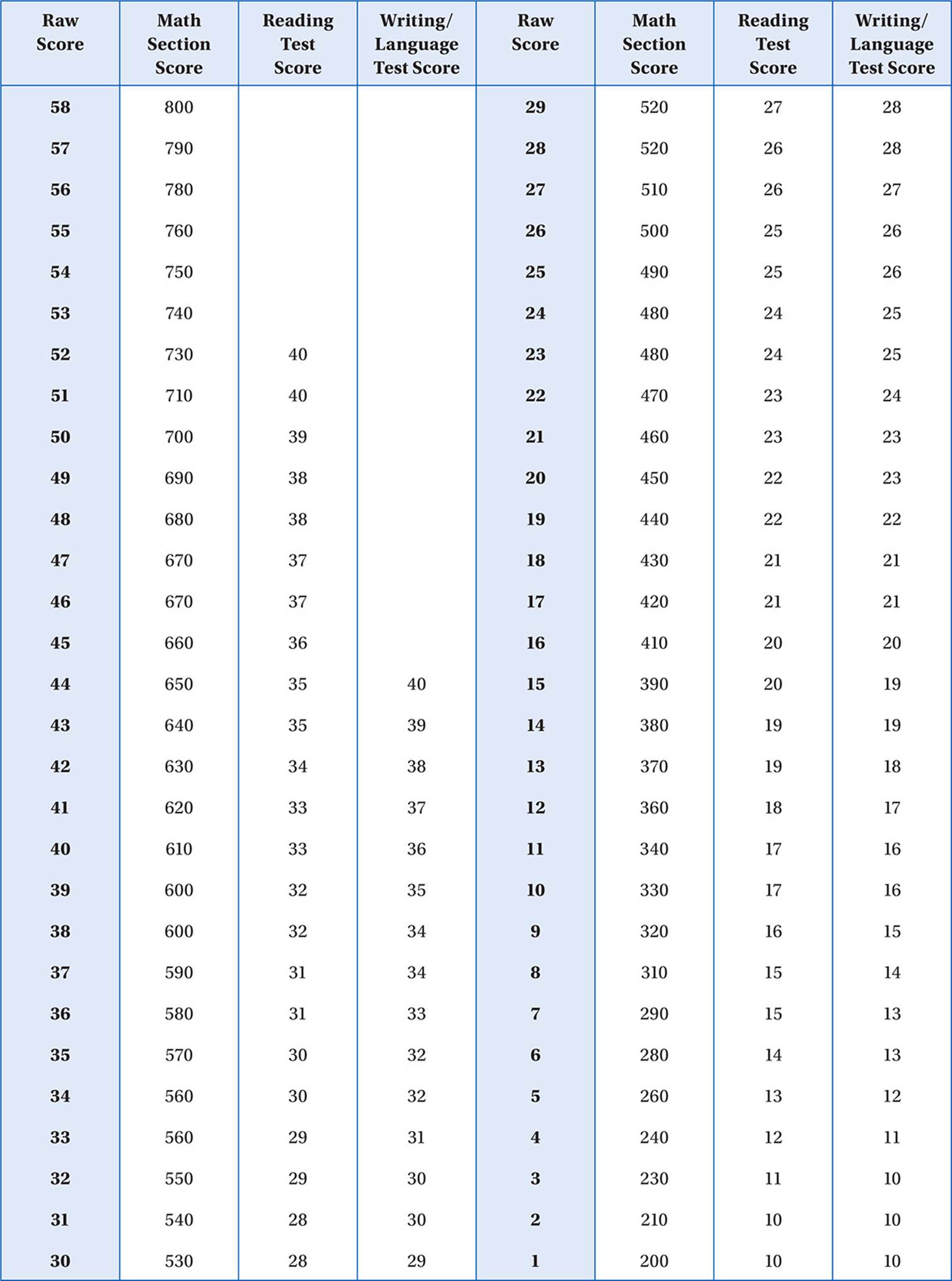
SCORE CONVERSION TABLE
Scoring Your Test
1. Use the answer key to mark your responses on each section.
2. Total the number of correct responses for each section:

3. Add the raw scores for sections 3 and 4. This is your Math Raw Score: _________________
4. Use the Table 1 to calculate your Scaled Test and Section Scores (10–40).

5. Add the Reading Test Scaled Score and the Writing and Language Test Scaled Score and multiply this sum by 10 to get your Reading and Writing Test Section Score (20–80).

Table 1: Scaled Section and Test Scores (10–40)
DIAGNOSTIC SAT DETAILED ANSWER KEY
Section 1: Reading
1. C
Specific Purpose
Let’s translate this question into a “stand-alone” question: “How is Smith’s work presented in the first paragraph?” The passage states (line 3) that Karl Smith has a good rule of thumb for categorizing epidemics, then goes on to describe various types of epidemics in an effort to help visualize the types of spread. In other words, he is proposing a model for conceptualizing phenomena. (Note that the word phenomena refers simply to common occurrences. It has a neutral tone, not a positive one.)
2. A
Inference
The passage states in lines 67–72 that Nevin’s paper was almost completely ignored because Nevin was an economist, not a criminologist, and his paper was published in Environmental Research, not a journal with a big readership in the criminology community. In other words, Nevin’s paper was ignored because it was not presented by authorities with the proper credentials.
3. C
Textual Evidence
As the explanation to question 2 indicates, the evidence for this answer is lines 67–72, which includes the statement in (C).
4. B
Inference from Data
According to the graph, in 1963 there were 150 violent crimes per 100,000 capita, and in 1993 there were 750 violent crimes per 100,000 capita. This is an increase of 600 crimes per 100,000, and 600 is 400% of 150.
5. D
Inference from Data
Nevin’s hypothesis is phrased in the form of a question in lines 27–28: Maybe reducing lead exposure had an effect on violent crime too? Therefore, the portion of the graph that would least support his hypothesis is the portion that shows the least correlation between lead exposure and crime. The biggest gap in the two graphs (and hence the portion that provides the least support for his thesis) corresponds to the set of violent crime statistics from 2003 to 2013.
6. C
Specific Purpose
The sales of vinyl LPs are mentioned to describe a statistic that also happens to correlate with preschool blood lead levels, thereby making the point that a single correlation between two curves isn’t all that impressive, econometrically speaking … No matter how good the fit, if you only have a single correlation it might just be coincidence. Hence, it is a statistic that may be more coincidental than explanatory.
7. D
Interpretation
The sentence in lines 21–24 indicates that lead exposure in small children [had been linked] with a whole raft of complications later in life, including lower IQ, hyperactivity, behavioral problems, and learning disabilities. These complications are psychological problems for those exposed to lead at a young age.
8. A
Interpretation
When the passage states that the drivers were unwittingly creating a crime wave two decades later (lines 63–64), it indicates that they were inadvertent abettors.
9. B
Word in Context
The phrase even better (line 49) refers to the finding mentioned in the previous sentence that the similarity of the curves was as good as it seemed, suggesting that the data showed an even stronger correlation than Nevin had hoped.
10. D
Specific Purpose
The final paragraph discusses the fact that the gasoline lead hypothesis explains many additional phenomena, such as the difference between the murder rates in large cities (where there are lots of cars) and small cities (where there are fewer cars and therefore less lead exhaust exposure). These implications further support the hypothesis.
11. B
Cross-Textual Inference
The author of Passage 1 indicates that Hemingway was a legendary figure whose work seemed … to have been carved from the living stone of life (lines 25–26) and therefore had a great impact on the author and his friends. Passage 2, however, suggests that Hemingway’s works don’t have the impact they once did, saying that they now seem unable to evoke the same sense of a tottering world that in the 1920s established Ernest Hemingway’s reputation (lines 48–50) and no longer seem to penetrate deeply the surface of existence (lines 57–58). Therefore, the two passages disagree most strongly on the incisiveness (deep analytical quality) of Hemingway’s work.
12. C
Textual Evidence
As the answer to the previous question indicates, the best evidence for this answer is found in lines 24–26 and lines 56–58.
13. C
Cross-Textual Interpretation
The author of Passage 1 regards Hemingway as a legend (line 16) whose impact upon us was tremendous (lines 18–19), but the author of Passage 2 calls Hemingway a dupe of his culture rather than its moral-aesthetic conscience (lines 66–67).
14. D
Cross-Textual Inference
The author of Passage 1 indicates that, although Hemingway’s work had a strong formative impact on him, it ultimately could not capture the true horrors of war that he and his friends were later to encounter:
The Hemingway time was a good time to be young. We had much then that the war later forced out of us, something far greater than Hemingway’s strong formative influence (lines 33–36).
Likewise, the author of Passage 2 indicates that Hemingway’s work did not fully capture the horrors of war: We have had more war than Hemingway ever dreamed of (lines 53–54) … yet Hemingway’s great novels no longer seem to penetrate deeply the surface of existence (lines 56–58).
15. A
Word in Context, Purpose
In saying that the words he put down seemed to us to have been carved from the living stone of life (lines 24–26), the author of Passage 1 means that Hemingway’s words represent living truths that have the weight and permanence of stone carvings. In other words, his words represent thesalient (prominent and important) experience of life.
16. D
Interpretation
In saying that we began unconsciously to translate our own sensations into their terms and to impose on everything we did and felt the particular emotions they aroused in us (lines 28–32) the author is saying that he and his friends identified with Hemingway’s language.
17. B
Inference
According to Passage 1, the lessons that [Hemingway] had to teach (line 43) included the example he set as a war correspondent writing a play in the Hotel Florida in Madrid while thirty fascist shells crashed through the roof (lines 10–12) and as a soldier defending his post singlehandedly against fierce German attacks (lines 13–15), both of which exemplify confidence in the face of danger.
18. D
Specific Purpose
The phrase a tottering world (line 49) is used to describe the Europe of the 1920s that Ernest Hemingway depicts in his novels. The author compares this world to one whose social structure is … shaken (lines 51–52) and which had more war than Hemingway ever dreamed of (line 54). In other words, a world filled with societal upheaval.
19. C
Cross-Textual Inference
The author of Passage 1 clearly views Hemingway as a personal and literary hero. Hence, a withering accusation such as the one in Passage 2 that Hemingway, in effect, became a dupe of his culture rather than its moral-aesthetic conscience (lines 66–67) would almost certainly be met withvehement disagreement.
Tip: Questions about how the author of one passage might most likely respond to some statement in another passage require us to focus on the thesis and tone of that author. Before attempting to answer such questions, remind yourself of the central theses of the passages.
20. B
Textual Evidence
The best evidence for this answer comes from lines 28–32, where the author of Passage 1 says that we began to unconsciously translate our own sensations into their terms and to impose on everything we did and felt the particular emotions they aroused in us. In other words, Hemingway was in fact a kind of moral-aesthetic conscience for the author of Passage 1 and his friends.
21. B
Interpretation
Passage 2 states that Hemingway’s novels yielded to the functionalist, technological aesthetic of the culture instead of resisting in the manner of Frank Lloyd Wright (lines 63–66). In other words, Frank Lloyd Wright was more iconoclastic (culturally rebellious) than Hemingway.
22. C
Specific Purpose
The first paragraph establishes the idea that atoms, the building blocks of everything we know and love … don’t appear to be models of stability, a fact that represents a scientific conundrum (riddle), because instability is not a quality that we expect of building blocks.
23. D
Word in Context
By asking [w]hy are some atoms, like sodium, so hyperactive while others, like helium, are so aloof? the author is drawing a direct contrast between chemical reactivity and relative nonreactivity.
24. D
Inference
This question, about why protons stick together in atomic nuclei, is the guiding question for the passage as a whole. The next paragraph analyzes this question in more detail, explaining why this well-known fact is actually so puzzling. The remainder of the passages discusses attempts to resolve this puzzle, which remains at the heart of quantum physics.
25. A
Textual Evidence
The evidence that this question represents a central conundrum is found in lines 1–5, where the author makes the uncontroversial claim that a sound structure requires stable materials, but then makes the paradoxical claim that atoms, the building blocks of everything we know and love … don’t appear to be models of stability.
26. A
Specific Purpose
The two sentences in lines 13–19 (We are told … electrons. We are also told … closer) indicate that we, the educated public, have been taught two seemingly contradictory facts about atoms. In other words, these are predominant conceptions.
27. C
Inference from Data
In the graph, the equilibrium point is indicated by a dashed vertical line labeled Equilibrium. If we notice where this line intersects the two curves, we can see that the corresponding electrostatic force is precisely opposite to the corresponding strong nuclear force. That is, the equilibrium point is where the two forces “cancel out” and have a sum of 0.
28. C
Inference from Data
Tip: When a question asks about a graph or table, it helps to circle the words or phrases in the question that correspond to the words or phrases in the graph or table. In this case, circle the key phrases electrostatic repulsion and separated by 1.5 femtometers in both the question and the graph.
Now, if we go to the graph and find the vertical line that corresponds to a separation of 1.5 femtometers, we can see that it intersects the curve for electrostatic force at the horizontal line representing 102, or 100, Newtons.
29. C
Interpretation
In the fourth paragraph, we are told that Hideki Yukawa proposed that the nuclear force was conveyed by a then-undiscovered heavy subatomic particle he called the pi meson (or “pion”), which (unlike the photon) decays very quickly and therefore conveys a powerful force only over a very short distance (lines 44–49). However, his theory was dealt a mortal blow by a series of experiments … that demonstrated that pions carry force only over distances greater than the distance between bound protons (lines 50–55). In other words, pions are ineffective in the range required by atomic theory, so they cannot be the carriers of the strong nuclear force.
30. B
General Structure
The first paragraph of this passage introduces the scientific conundrum of how protons adhere in atomic nuclei. The second paragraph analyzes this strange situation. The third paragraph describes a force, the strong nuclear force, that could solve the conundrum. The fourth paragraph describes a particular theory, now refuted, about what might convey this strong nuclear force. The fifth and sixth paragraphs indicate that the problem has yet to be satisfactorily resolved. Thus, the passage as a whole is a description of a technical puzzle and the attempts to solve it.
31. A
Literary Devices
A rhetorical question is a question intended to convey a point of view, rather than suggest a point of inquiry. Although the first and second paragraphs include five questions, they are all inquisitive, not rhetorical.
The passage includes illustrative metaphors in lines 15–16 (a cloud of speedy electrons) and lines 55–56 (a plumber’s wrench trying to do a tweezer’s job), technical specifications in lines 29–40 (First, it can’t have … each other), and appeals to common intuition in lines 1–2 (a sound structure … materials) and lines 13–16 (We are . . . electrons).
32. B
Word in Context
The hope that QCD ties up atomic behavior with a tidy little bow is the hope that the QCD theory resolves the problem in a tidy way.
33. C
General Purpose
The passage as a whole develops the thesis that the wise legislator does not begin by laying down laws good in themselves, but by investigating the fitness of the people, for which they are destined, to receive them (lines 3–6). In other words, the passage is concerned with examining the social conditions that foster effective legal systems.
34. C
Word in Context
In saying that the architect sounds the site to see if it will bear the weight, the author means that the architect probes the proposed location for a building to make sure that it is safe to build upon.
35. A
Specific Purpose
The analogy of the architect in the first paragraph illustrates the thesis of the passage that the wise legislator does not begin by laying down laws good in themselves, but by investigating the fitness of the people, for which they are destined, to receive them (lines 3–6). That is, that a nation’s civil code depends on the nature of its people. Choice (B) is incorrect because the analogy is not about the foundational principles of laws, but rather the fitness of the people for whom they are intended.
36. A
Inference
The author states that as a nation grows older, its citizens become incorrigible (unable to be improved) . Once customs have become established and prejudices inveterate (deep-seated), it is dangerous and useless to attempt their reformation (lines 19–21). That is, the people become stubbornly resistant to political change.
37. B
Textual Evidence
As the explanation to the previous question indicates, the relevant evidence is found in lines 20–21.
38. B
Interpretation
When the author says that [m]ost peoples, like most men, are docile only in youth (lines 17–18), he is saying that societies (the peoples) as well as individuals (men) become less manageable as they age.
39. B
Specific Purpose
The author refers to Sparta at the time of Lycurgus (line 35) as an example of a state, set on fire by civil wars, [which] is born again (lines 31–32). That is, a society rejuvenated by conflict. Choice (A) may seem tempting, because the beginning of the paragraph mentions the fact that periods of violence (lines 28–29) can make people forget the past, but the paragraph explains that this forgetting has the effect of renewal, not paralysis.
40. B
Interpretation
Although the word constitution can be used to mean the documented rules by which a nation defines its governmental institutions (as in the Constitution of the United States of America), the phrase the constitution of the state, as it is used in this passage, clearly refers to the composition of the state, that is, the people who constitute the nation.
41. A
Interpretation
In saying that [o]ne people is amenable to discipline from the beginning; another, not even after ten centuries (lines 51–53), the author means that some nations are ready to be governed by the rule of law as soon as they are founded, but others require much more time.
42. D
Inference
The passage states that Peter the Great … lacked true genius [because he] did not see that [his nation] was not ripe for civilization: he wanted to civilize it when it needed only hardening (lines 55–61). In other words, he did not give his nation the hardening it needed: his flaw was hisirresolution (hesitancy due to a lack of conviction) in exerting control.
43. C
General Purpose
The first sentence of the passage establishes its central purpose: to understand the views of Aristotle, and asserts that to do this it is necessary to apprehend his imaginative background (lines 1–3). In other words, the purpose of this passage is to describe the conceptions that inform a particular mindset.
44. B
Interpretation
When the author states that Animals have lost their importance in our imaginative pictures of the world (lines 29–30), he is reinforcing his point that modern students are accustomed to automobiles and airplanes; they do not, even in the dimmest recesses of their subconscious imagination, think that an automobile contains some sort of horse inside, or that an airplane flies because its wings are those of a bird possessing magical powers (lines 23–29). In other words, animistic beliefs no longer inform our physical theories.
45. D
Interpretation
When the author states that every philosopher, in addition to the formal system that he offers to the world, has another much simpler system of which he may be quite unaware (lines 3–6), the simpler system refers to the imaginative background (line 3) that informs a scientist’s formal theories. However, if a scientist is aware of this simpler system, he probably recognizes that it won’t do (line 7). Therefore, this system is a relatively unrefined way of thinking.
46. A
Inference
In lines 61–65, the author states that It was natural that a philosopher who could no longer regard the heavenly bodies themselves as divine should think of them as moved by the will of a Divine Being who had a Hellenic love of order and geometric simplicity. In other words, the astronomical theories of some ancient Greek philosophers were closely associated with their religious ideas.
47. A
Textual Evidence
As the explanation to the previous question indicates, the evidence for this answer is in lines 61–65.
48. D
Word in Context
When the author states that, to the Greek, it seemed more natural to assimilate apparently lifeless motions to those of animals (lines 46–47), he means that the ancient Greeks found it easy to liken the motion of machines to the motion of animals.
49. D
Inference
The passage states that To the ancient Greek, attempting to give a scientific account of motion, the purely mechanical view hardly suggested itself, except in the case of a few men of genius such as Democritus and Archimedes. In other words, most Greeks were not inclined toward the mechanical view, except for the men of genius, who had more accurate metaphors for the laws of motion, and therefore were “willing to disregard conventional wisdom.”
50. C
Inference
As it is discussed in the passage, the apparent gulf between animals and machines (lines 44–45) is the ever-shrinking gap between the animistic and the mechanistic view of animal physiology. To the modern scientist, each piece of evidence that demonstrates how the body of an animal is a very elaborate machine, with an enormously complex physical and chemical structure (lines 41–43) serves to bridge this gulf. One example of such evidence might be the mechanical laws that describe bumblebee flight.
51. B
Inference
The first paragraph discusses the fact that the views of Aristotle (line 1) are due to his imaginative preconceptions, or to what Santayana calls “animal faith” (lines 17–18), which the author goes on to explain include animistic tendencies, that is, tendencies toward seeing living spirits in all physical phenomena .
52. D
Textual Evidence
Lines 45–47 also reinforce the author’s point that Aristotle, like other ancient Greeks, was inclined toward an animistic view of the world: To the Greek, it seemed more natural to assimilate apparently lifeless motions to those of animals.
Section 2: Writing and Language
1. B
Subject-Verb Agreement
The subject of this verb is demand, which is singular. Therefore, are must be changed to is.
2. C
Diction
This question asks you to choose the word that best fits the semantic context of the sentence, that is, the word that helps the sentence to convey a logical idea in the context of the paragraph.
This previous sentence states that an important challenge facing the healthcare industry is how to address this shortfall without sacrificing quality of care. Among our options, the only one that suggests a possible solution to this problem is to incentivize more medical school graduates to choose primary care.
Although it may seem that interest is a reasonable choice, notice that its use would violate idiom in this sentence: the correct idiom is not interest someone to do something, but rather interest someone in doing something.
3. C
Logical Comparisons
This portion of the sentence is part of a parallel construction in the form A instead of B. In such constructions, the words or phrases in A and B must have the same grammatical form and describe logically comparable (or contrastable) things. Since in this case A is primary care (a noun phrase indicating a medical specialty), the most logical choice for B is the more lucrative specialties (a noun phrase indicating medical specialties). The original phrasing is incorrect because their choosing does not indicate a medical specialty, (B) is incorrect because to choose does not indicate a medical specialty, and choice (D) is incorrect because it is redundant.
4. A
Parallelism
Words or phrases in a list should have the same grammatical form. In the original phrasing, the three items in the list are all present tense verbs: talk … prescribe … perform.
5. B
Diction
Because a “team-based” model is not a location, the use of the pronoun where is incorrect. Likewise, choice (D) when is incorrect because a “team-based” model is not a time. Choice (C) is incorrect because it produces a comma splice. The correct answer is (B) whereby, which means by which.
6. C
Diction
The adverb still means even now or nevertheless, neither of which fit the logical context of this sentence. Only choice (C) while, meaning at the same time, fits logically. Choice (B) while at the same time is redundant, and choice (D) although implies a contrast, which is illogical.
7. A
Coordination of Ideas, Cross-References
The subject of the inserted sentence is these professionals. The pronoun these requires an antecedent, which is best provided if the sentence is placed after sentence 1, which specifies medical professionals like physician assistants (PAs) and nurse practitioners (NPs).
8. D
Data Analysis
The descending line in the graph shows clearly that the percentage of PAs in primary care has declined from 51% in 2000 (over one-half) to 31% in 2010 (under one-third).
9. A
Logical Comparisons, Pronoun-Antecedent Agreement
This sentence is correct as written. The pronoun they agrees in number and kind with its antecedent students, and the comparison is logical. Choice (D) is redundant.
10. D
Idiom, Pronoun-Antecedent Agreement
Using the phrase being that to mean because is colloquial and nonstandard for written American English, therefore choices (A) and (C) are incorrect. Choice (B) is incorrect because when should only be used to refer to a time.
11. D
Pronoun-Antecedent Agreement, Cross-References
The definite pronoun they must refer to some plural noun, but the only possible plural antecedent in this sentence is programs, which would be illogical. Choice (D) clarifies the reference.
12. C
Punctuation
The four choices differ only in their punctuation. Any reference to a city-and-country or city-and-state must separate the two with commas: e.g. London, England or Providence, Rhode Island. Therefore the original punctuation in (A) is incorrect. Choice (B) is incorrect because it produces a sentence fragment. Choice (D) is incorrect because it misuses the semicolon: the two phrases on either side of the semicolon should be independent clauses.
13. B
Logic, Dangling Participles
Since engineering is a class of profession and not a position, the original phrasing is illogical. Choice (C) is incorrect because it is a dangling participial phrase: the past participle considered does not share a subject with the main clause. Choice (D) is incorrect because the phrase in reputation is not idiomatic.
14. D
Dangling Participles
The sentence begins with the participial phrase suffering ridicule and isolation. Any participial phrase must have the same subject as the main clause. In the original phrasing, the subject of the main clause is Montessori’s medical studies, but this cannot be the subject of suffering ridicule and isolation. Therefore, choices (A) and (C) are both incorrect. Choices (B) and (D) both correct this problem by changing the subject of the main clause to Montessori, but (B) is incorrect because the phrase by becoming is illogical.
15. A
Parallelism
This sentence contains the parallel construction A rather than B. The original phrasing provides parallel phrasing: respect and stimulation shares the same grammatical form and semantic category as the regimentation. Choice (D) provides a parallel phrasing but illogically implies that the students were receiving institutions.
16. B
Diction, Agreement
The original phrasing is incorrect because they’re is a contraction of they are, which is illogical in this context. Choice (C) is incorrect because childrens’ is not a word at all. Children is the plural form of child, and the possessive form of children is children’s. Choice (D) is incorrect becausetheir disagrees in number with the antecedent each.
17. C
Diction
This sentence discusses how word of Montessori’s success with her school began to spread of its own merit and accord. Choices (A) and (D) are incorrect because both distribute and exhibit imply intentional action. Choice (B) is illogical: word of someone’s success cannot increase.
18. D
Logical Cohesiveness
To understand which sentence most effectively introduces this paragraph, we must first understand what the paragraph is about. As a whole, the paragraph discusses how Montessori schools were regarded as a remedy to the educational programs associated with rapid urban population growth in Europe … but then came to be seen as a threat to the power of the state. Choice (D) encapsulates this idea the best.
19. C
Logical Transitions
Choice (C) provides the most logical transition between ideas in the paragraph: the shift from a positive view of Montessori’s work to a negative view requires a contrasting transition like however.
20. D
Redundancy
The original phrasing is redundant: being subversive is the same as undermining power. The most concise correct phrasing is that in (D).
21. B
Subject-Verb Agreement
In the original phrasing, the subject response (singular) disagrees with the verb were (plural) divided. Choice (B) provides the most effective correction.
22. A
Logical Cohesiveness
The remarkable thing about this paragraph is its introduction of dissenting views on Montessori’s work from within the field of education, rather than merely from political opponents. Any additional discussion in this paragraph should elaborate on the nature of that dissent in the educational community. Only choice (A) extends the discussion in a relevant way.
23. D
Redundancy
This sentence is asserting a claim that directly contrasts the point of view presented in the previous paragraph. Choice (D) In fact, introduces just such an assertion. Choice (A) First is incorrect because this claim is not part of an enumerated list. Choice (B) So is incorrect, because this sentence is not asserting a logical consequence of the previous claim. Choice (C) While is incorrect because it produces a sentence fragment.
24. C
Diction, Idiom
The original phrasing is incorrect because the phrase complies [to] is not idiomatic. The same is true of (B) overlaps [to] and (D) concurs [to]. Choice (C) corresponds [to], however, is idiomatic and logical.
25. A
Coordination of Ideas
This phrase is correct as written. It is expressing a condition, and so the use of the conjunction if is correct.
26. D
Dangling Participles
The participle pondering and the main clause must share the same subject, or else the participle “dangles.” Who was pondering? Plato. Therefore Plato must be the subject of the main clause. Choice (C) is incorrect, however, because there is no need for the past participle form had argued.
27. C
Parallelism
The sentence contains the parallel construction A yet B. The phrasing inaccessible … yet apprehensible provides a parallel form, since both inaccessible and apprehensible are adjectives.
28. B
Modifier Usage
The phrase between the commas is an interrupting modifier. Any sentence should remain grammatically complete even when any interrupting modifier is removed. Notice that if we did this with the original sentence, it would read as effective … than sensory experience, which is clearly unidiomatic. (The correct comparative idiom is as effective as.) The only choice that corrects this problem is (B).
29. C
Logical Cohesiveness
The information the author is proposing does not fit with the discussion about the philosophy of Platonic idealism.
30. D
Modifier Form
In the original phrasing, the conjunction and is incorrect because it does not conjoin comparable words or phrases; therefore, choices (A) and (C) are incorrect. In choice (B) the prepositional phrase in not having to believe is illogical. Choice (D) is correct because the prepositional phrasewithout having to believe logically modifies the verb understand.
31. A
Possessives
This sentence is correct as written. Choice (B) is incorrect because the pronoun they has no clear antecedent. Choice (C) misuses the possessive brain’s, and choice (D) yields the subject-verb disagreement brain make.
32. C
Verb Mood
This clause is part of a counterfactual hypothesis. As we discuss in Chapter 4, Lesson 30, a present counterfactual hypothesis takes the form of the present subjunctive mood, which is usually the same form as the simple past tense: existed.
33. B
Pronoun Consistency
Since the previous sentence refers to our brains, pronoun consistency requires that this sentence continue to use the first-person plural pronoun we.
34. B
Coordination of Clauses
The interrupting modifier (perhaps while showering or driving) must be “bracketed” on either end by commas, em dashes, or parentheses. Since it clearly ends with an em dash, it must start with an em dash as well.
35. A
Pronoun Form
This sentence is correct as written. Choice (B) uses the wrong pronoun form what and incorrectly implies that Archimedes is shouting in the present. Choice (C) uses the wrong pronoun form that and misplaces the modifying clause it is said. Choice (D) misuses the past perfect form had shouted.
36. B
Diction
The sentence discusses the relationship between the feeling of the Eureka effect and a fundamentally different way of thinking. In the context of the discussion, the only choice that indicates a logical relationship is (B): this feeling indicates a different way of thinking.
37. D
Coordination of Clauses
The original phrasing is incorrect because it includes a comma splice. Choice (B) is incorrect because the prepositional phrase by which is illogical. In choice (C), the use of the pronoun where is incorrect because an experiment is not a place.
38. C
Subject-Verb Agreement, Redundancy
The verb requires (singular) disagrees with the subject tasks (plural), therefore choices (A) and (D) are incorrect. Choice (B) is redundant.
39. C
Subject-Verb Agreement
The modifying phrase as soon as solving it is vague and awkward. Choice (C) clarifies the modifier by indicating that the subjects are solving the task.
40. D
Awkwardness, Logical Transitions
The underlined phrase is a sentence modifier, that is, a phrase that modifies the statement in the main clause experimenters found. Choices (A), (B), and (C) are needlessly awkward and wordy, but choice (D) provides a concise and clear modifier.
41. B
Verb Tense
This clause is describing a general fact (the theory that . . .), not an event. To express general facts, we use the simple present tense: corresponds.
42. B
Data Analysis
According to the graph, the line indicating the Insight condition separates from the line representing the Non-insight condition approximately 0.3 seconds prior to the button being pushed, and remains elevated until about 0.7 seconds after the button is pushed, for a duration of approximately 1 second.
43. D
Pronoun-Antecedent Agreement, Subject-Verb Agreement
The verb is agrees with the subject interpreting (both are singular), but the pronoun this disagrees with its antecedent data (this is singular, but data is plural).
44. B
Coordinating Clauses
The correct choice should combine the two questions into a single sentence. Choice (A) misstates the second question. Choice (C) inappropriately uses the subjunctive mood. Choice (D) misuses the parallel construction both A and B.
Section 3: Math (No Calculator)
1. B
Algebra (solving equations) EASY
6x + 9 = 30
To solve in one step, just divide both sides by 3:
2x + 3 = 10
Most students waste time solving for x, which will work, but takes longer:
6x + 9 = 30
Subtract 9:
6x = 21
Divide by 6:
x = 3.5
Evaluate 2x + 3 by
substituting x = 3.5:
2x + 3 = 2(3.5) + 3 = 7 + 3 = 10
2. D
Advanced Mathematics (nonlinear systems)
EASY
The solutions to the system correspond to the points of intersection of the two graphs. The figure shows four such intersection points.
3. B
Algebra (algebraic expressions) EASY
Let a = # of adult tickets sold, and c = # of child tickets sold. If 300 tickets were sold altogether:
c + a = 300
The revenue for a adult tickets sold at $5 each is $5a, and the revenue for c child tickets sold at $3 each is $3c. Since the total revenue is $1,400:
5a + 3c = 1,400
4. A
Advanced Mathematics (polynomials) EASY
2(x − 4)2 − 5x
Factor:
2[(x − 4)(x − 4)] − 5x
FOIL:
2[ x2 − 4x − 4x + 16] − 5x
Simplify:
2[ x2 − 8x + 16] − 5x
Distribute:
2x2 − 16x + 32 − 5x
Combine like terms:
2x2 − 21x + 32
5. C
Special Topics (three-dimensional geometry) MEDIUM
On the drawing, we should first mark the areas of the three faces. The front and back faces both have an area of 3a. The left and right faces both have an area of 3b. The top and bottom faces both have an area of ab. We should now try to find integer values for a and b so that these areas match those given in the choices.
(A) 15, 18, and 30
This is possible if a = 5 and b = 6.
(B) 18, 24, and 48
This is possible if a = 6 and b = 8.
(C) 12, 15, and 24
This cannot work for any integer values of a and b.
(D) 15, 24, and 40
This is possible if a = 5 and b = 8.
6. D
Algebra (linear equations) MEDIUM
C(n) = an + b
Since this expression is linear in n (the input variable, which represents the number of necklaces produced), the constant a represents the slope of this line, which in turn represents the “unit rate of increase,” in other words, the increase in total cost for each individual necklace produced.
The constant b represents the “y-intercept” of this line, which in this case means the costs when n = 0 (that is, the fixed costs before any necklaces are produced).
7. A
Algebra (lines) MEDIUM
To find the slope of line l, we can find two points on l and then use the slope formula.
f(x) = 2x2 − 4x +1
Plug in −1 for x:
f(−1) = 2(−1)2 − 4(−1) + 1
Simplify:
f(−1) = 2(1) + 4 + 1 = 2 + 4 + 1 = 7
Therefore line l intersects the function at (−1, 7).
Plug in 2 for x:
f(2) = 2(2)2 − 4(2) + 1
Simplify:
f(2) = 2(4) − (8) + 1 = 8 − 8 + 1 = 1
Therefore line l intersects the function at (2, 1). Now we find the slope of the line containing these two points.
slope 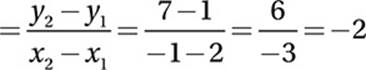
8. B Advanced Mathematics (parabolas) MEDIUM
The general equation of a parabola in the xy-plane is y = a(x − h)2 + k, in which (h, k) is the vertex. Now let’s express each choice in precisely this form.
(A) y = (x − 3)2 + 2 y = 1(x − 3)2 + 2a = 1, h = 3, k = 2
(B) y = 2(x − 3)2 y = 2(x − 3)2 + 0a = 2, h = 3, k = 0
(C) y = 2x2 − 3 y = 2(x − 0)2 − 3a = 2, h = 0, k = −3
(D) y = 3x2 + 2 y = 3(x − 0)2 + 2a = 3, h = 0, k = 2
If this vertex is on the x-axis, then k = 0. The only equation in which k = 0 is (B).
9. D Advanced Mathematics (rational equations) MEDIUM
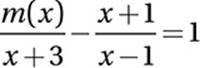
Add 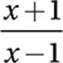 :
:
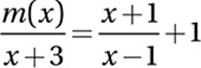
Express right side in terms of a common denominator:
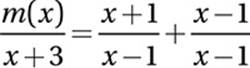
Combine terms on right into one fraction:
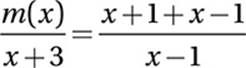
Combine terms:
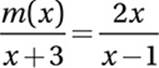
Multiple by x + 3:
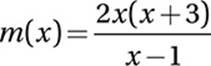
10. C
Algebra (linear relationships) MEDIUM
We are told that the temperature varies linearly with altitude, so if y represents the temperature (in °C) and x represents altitude (in km), these variables are related by the equation y = mx + b, where m (the slope) and b (the y-intercept) are constants.
We are given two points on this line: (50 km, 10°) and (80 km, −80°). We can use these points to find the slope, m:
slope 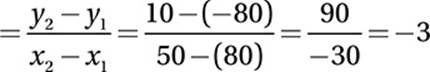
Recall that the slope of a linear relationship is the “unit rate of change.” In other words, the slope of −3 means that the temperature declines by 3° for every 1 km of additional altitude. Since we want the altitude at which the temperature is −50°, we want the value of x such that (x, −50°) is on this line. To find x, we can simply use the slope formula again, using either of the other two points: Slope formula using (50, 10) and (x, −50):
slope 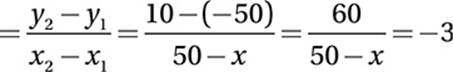
Multiply by 50 − x:
60 = −3(50 − x)
Distribute:
60 = −150 + 3x
Add 150:
210 = 3x
Divide by 3:
70 = x
11. A Advanced Mathematics (triangles/quadratics) MEDIUM-HARD
Any point that intersects the y-axis has an x-value of 0. So, to find point A, plug in 0 for x and solve for y:
y = 2x2 − 16x + 14
Plug in 0 for x:
y = 2(0)2 − 16(0) + 14 = 14
Any point that intersects the x-axis has a y-value of 0. So, to find points B and C, plug in 0 for y and solve for x:
y = 2x2 − 16x + 14
Substitute 0 for y:
0 = 2x2 − 16x + 14
Divide by 2:
0 = x2 − 8x + 7
Factor:
0 = (x − 7)(x − 1)
Use the Zero Product Property:
x = 7 and x = 1
If we connect these three points, we get a triangle with a height of 14 (from y = 0 to y = 14) and a base of 6 (from x = 1 to x = 7).
Use the triangle area formula 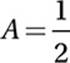 bh:
bh:
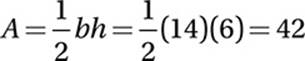
12. B Advanced Mathematics (polynomials) MEDIUM-HARD
Given equation:
y = (x + 2)2 (x − 3)2
To find the y-intercept, set x = 0:
y = (0 + 2)2(0 − 3)2
Simplify:
y = (2)2(-3)2 = (4)(9) = 36
Therefore the y-intercept is at (0, 36).
To find the x-intercepts, set y = 0:
0 = (x + 2)2 (x − 3)2
By the Zero Product Property, the only solutions to this equation are x = −2 and x = 3, so there are two x-intercepts and a total of three x- and y-intercepts.
13. C
Special Topics (complex numbers) HARD
A(2 − i) = 2 + i
Divide by (2 − i):
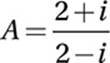
Multiply numerator and denominator by the conjugate (2 + i):
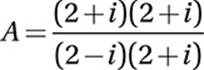
FOIL:
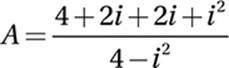
Combine terms:
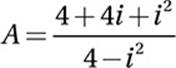
Substitute i2 = − 1:
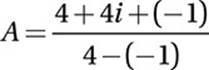
Simplify:
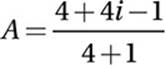
Combine terms:
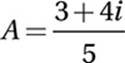
Distribute to express in standard a + bi form:
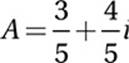
14. B
Algebra (graphs of linear equations) HARD
Given equation:
y + x = k(x − 1)
Subtract x:
y = k(x − 1) − x
Distribute:
y = kx − k − x
Collect like terms:
y = (k − 1)x − k
The slope of this line is k − 1 and its y-intercept is − k. If k > 2, then k − 1 > 1, and − k < −2. In other words, the slope of the line is greater than 1 and the y-intercept is less than −2. The only graph with these features is the one in choice (B).
15. B
Advanced Mathematics (analyzing polynomial functions) HARD
Because this polynomial has a degree of 3 (which is the highest power of any of its terms), it cannot have more than 3 zeros. These three zeros are given as −2, 3, and 6. We also know that g(0), the y-intercept of the graph, is negative. This gives us enough information to make a rough sketch of the graph.
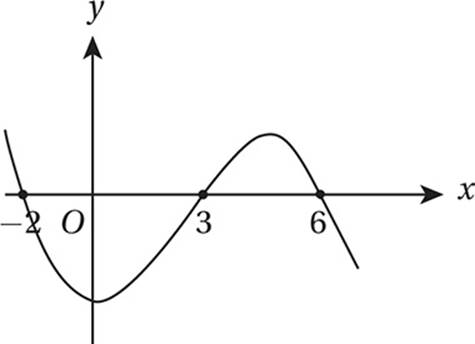
This shows that the only values of x for which the function is negative are −2 < x < 3 and x > 6. Therefore the only negative value among the choices is (B) g(−1).
16. 30
Algebra (linear equations) EASY
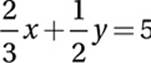
Multiply by 6 (the common denominator):
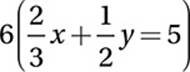
Distribute:
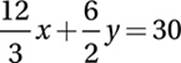
Simplify:
4x + 3y = 30
17. 25/7 or 3.57
Advanced Mathematics (rational equations) EASY
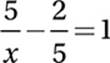
Add ![]() :
:
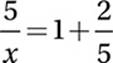
Simplify:
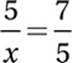
Cross multiply:
25 = 7x
Divide by 7:
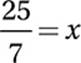
18. 35
Special Topics (radians and arcs) MEDIUM-HARD
Since an arc is simply a portion of a circumference, let’s first calculate the circumference of the circle:
C = 2πr = 2π(36) = 72π
Because arc AB has a measure of 7π, it is 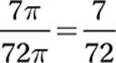 of the entire circumference. Since x° is the measure of the central angle that corresponds to this arc, it must be the same fraction of the whole:
of the entire circumference. Since x° is the measure of the central angle that corresponds to this arc, it must be the same fraction of the whole:
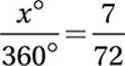
Cross multiply:
72x = 7(360)
Divide by 72:
x = 7(5)
Simplify:
x = 35
19. 1.2
Algebra (linear systems) MEDIUM-HARD
First, we should simplify the first equation:
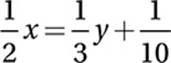
Subtract ![]() y:
y:
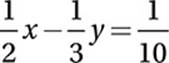
Multiply by 12:
6x − 4y = 1.2
This equation represents a line with slope of  . The second equation, 6x − 4y = k, also represents a line with slope
. The second equation, 6x − 4y = k, also represents a line with slope  . In order for this system of equations to have at least one solution, these two lines must have an intersection. How can two lines with the same slope intersect? They must be identical lines, and therefore intersect in all of their points. If this is the case, then k must equal 1.2.
. In order for this system of equations to have at least one solution, these two lines must have an intersection. How can two lines with the same slope intersect? They must be identical lines, and therefore intersect in all of their points. If this is the case, then k must equal 1.2.
20. 2.4
Special Topics (trigonometry) HARD
Since x represents the radian measure of an acute angle, and sin 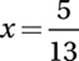 , we can use the definition of sine
, we can use the definition of sine 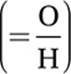 to draw a right triangle:
to draw a right triangle:
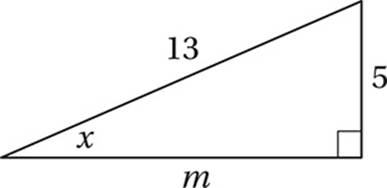
We might notice that this is a 5-12-13 special right triangle, or simply use the Pythagorean Theorem to show that m = 12. We can also show that the other acute angle in the triangle must be complementary to x (that is, together they form a right angle), and so must have a measure of ![]() −x.
−x.
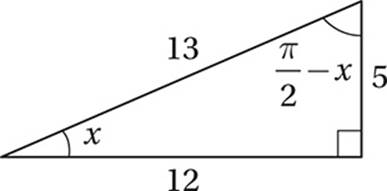
To find tan 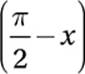 , we simply have to use the angle with measure
, we simply have to use the angle with measure 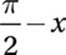 as our new reference angle, and use TOA:
as our new reference angle, and use TOA:
tan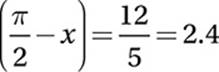
Section 4: Math (Calculator)
1. D
Algebra (systems) EASY
When faced with a system of equations, notice whether the two equations can be combined in a simple way—either by subtracting or adding the corresponding sides—to get the expression the question is asking for.
a − b = 10
a − 2b = 8
Subtract corresponding sides:
b = 2
2. C
Data Analysis (central tendency) EASY
The average of three numbers is 50:
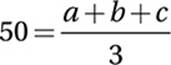
Multiply by 3:
150 = a + b + c
Two of the numbers have a sum of 85:
85 = a + b
Substitute into the previous equation:
150 = 85 + c
Subtract 85 to find c:
65 = c
3. D
Problem Solving/Data Analysis (proportions) EASY
Set up a proportion:
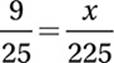
Cross multiply:
2,025 = 25x
Divide by 25:
81 = x
4. B
Data Analysis (tables) EASY
Let’s fill in the table with the information we’re given and work our way to the value the question asks us to find. First, use the information in the FAVORABLE column to determine how many women viewed the politician favorably:
26 + w = 59
Subtract 26:
w = 33
Next, go to the WOMEN row:
33 + x + 13 = 89
Combine terms:
46 + x = 89
Subtract 46:
x = 43
5. D
Algebra (exponentials) EASY
22n − 2 = 32
When dealing with exponential equations, it helps to see if we can express the two sides of the equation in terms of the same base. Since 32 = 25, we can express both sides in base 2:
22n − 2 = 25
If xa = xb and x > 1, then a = b (if the bases are equal, the exponents are equal):
2n − 2 = 5
Add 2:
2n = 7
Divide by 2:
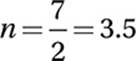
6. C
Algebra (representing quantities) EASY
The question asks us to find the “part-to-whole” ratio of walnuts: walnut fraction 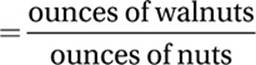 .
.
Since the walnuts weigh x ounces, and the total weight of all the nuts is x + 15 + 20 = x + 35 ounces,
walnut fraction 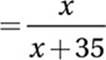
7. B
Advanced Mathematics (triangle trigonometry) EASY
Remember the definitions of the basic trigonometric functions: SOH CAH TOA. Since the “side of interest” (k) is the OPPOSITE side to the given angle (35°), and since we know the length of the HYPOTENUSE (12), we should use SOH.
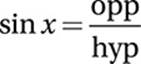
Plug in the values:
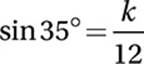
Substitute sin 35° = 0.574:
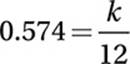
Multiply by 12:
(12)(0.574) = 6.88 = k
8. A
Special Topics (polygons) EASY
The sum of the measures if the interior angles of any polygon is (n − 2)180°, where n is the number of sides in the polygon. Since this is a 5-sided polygon, the sum of its interior angles is (5 − 2)(180°) = 3(180°) = 540°. Therefore the average of these measures is 540°/5 = 108°.
9. B
Data Analysis (scatterplot) MEDIUM
We want to find the slope of the line of best fit because it represents the average annual increase in revenue per store. Although the question asks about the years 2004 and 2012, we can choose ANY two points on this line to find its slope. We should choose points on the line of best fit that are easy to calculate with, such as (2005, $300,000) and (2011, $600,000).
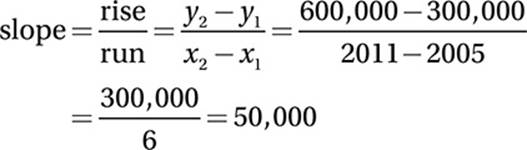
10. C
Data Analysis (scatterplot) MEDIUM-HARD
When faced with a question like this, we must analyze each statement individually.
(A) The average revenue per store increased by over 100% from 2005 to 2009. True or false? In 2005, according to the line of best fit, the average revenue per store was approximately $300,000. In 2009, the average revenue per store was approximately $500,000. This is a percent increase of
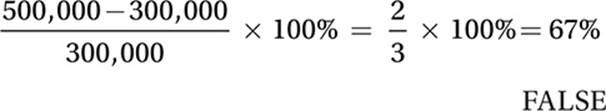
(B) The total number of retail stores increased by 50% from 2005 to 2012. True or false? According to the scatterplot, in 2005 there were 3 stores corresponding to the three dots above 2005. In 2012 there were 6 stores corresponding to the 6 dots above 2012. This is a percent increase of

FALSE
(C) The total revenue for all stores in 2012 is more than three times the total revenue from all stores in 2004. True or false? In 2004, there were 3 stores with an average revenue per store of approximately $250,000. Therefore the total revenue in 2004 was approximately 3 × $250,000 = $750,000. In 2012, there were 6 stores with an average revenue per store of approximately $650,000. Therefore the total revenue in 2012 was approximately 6 × $650,000 = $3,900,000. Since $3,900,000 is more than three time $750,000, this statement is TRUE.
11. B
Algebra (translating quantitative information) MEDIUM
This question tests your ability to translate words into algebraic expressions. Systematically translate the sentence phrase by phrase.
The product of two numbers, a and b is 6 greater than their sum.
Translation:
ab = 6 + a + b
Use commutative law of equality on right side:
ab = a + b + 6
12. D
Special Topics (coordinate geometry) MEDIUM
First, find the slope of l using the points (0, −9) and (12, 0):
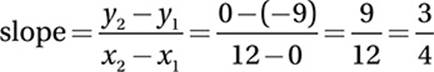
Since the two lines are parallel, line m must also have a slope of ![]() . Now we can solve for k using the slope equation and the two points on line m, (0, 0) and (k, 12):
. Now we can solve for k using the slope equation and the two points on line m, (0, 0) and (k, 12):
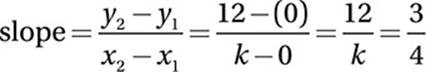
Cross multiply:
4(12) = 3(k)
Simplify:
48 = 3k
Divide by 3:
16 = k
Notice that the coordinates of the point (16, 12) correspond to the width and the length of the rectangle, respectively. Therefore, the area of the rectangle is 16 × 12 = 192 square units.
13. A
Problem Solving/Data Analysis (ratios) MEDIUM
If the Giants’ win-loss is 2:3, then they won 2n games and lost 3n games, where n is some unknown integer. (For instance, perhaps they won 2 games and lost 3, in which case n = 1, or perhaps they won 20 games and lost 30, in which case n = 10, etc.) This means that the total number of games they played is 2n + 3n = 5n. Since they won 120 games,
5n = 120
Divide by 5:
n = 24
Therefore they won 2n = (2)(24) = 48 games and lost 3n = (3)(24) = 72 games, and so they lost 72 − 48 = 24 more games than they won.
14. B
Advanced Mathematics (exponential growth) MEDIUM
We might begin by plugging in a number for p. Let’s say p = 120 cells to start. We are told that after one hour the population decreased by ![]() . Since
. Since ![]() of 120 is 40, the population decreased by 40 and the population was then 120 − 40 = 80 cells. In the second hour, the population increasedby 40%. Increasing a number by 40% is equivalent to it by 1.40 (because it becomes 140% of what it was), so the population was then 80(1.40) = 112 cells. In the third hour, the population increased by 50%, so it became 112(1.50) = 168 cells.
of 120 is 40, the population decreased by 40 and the population was then 120 − 40 = 80 cells. In the second hour, the population increasedby 40%. Increasing a number by 40% is equivalent to it by 1.40 (because it becomes 140% of what it was), so the population was then 80(1.40) = 112 cells. In the third hour, the population increased by 50%, so it became 112(1.50) = 168 cells.
Substituting p = 120 into each of the answer choices yields (A) 1.3p = 1.3(120) = 156, (B) 1.4p = 1.4(120) = 168, (C) 1.5p = 1.5(120) = 180, and (D) 1.6p = 1.6(120) = 192. Therefore the answer is (B).
Alternately, you can solve this problem algebraically: p(2/3)(1.40)(1.50) = 1.40p.
15. B
Advanced Mathematics (exponentials) MEDIUM
For this one, we’ll need the Laws of Exponentials from
Chapter 9, Lesson 9.
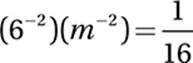
Translate by using Exponential Law #3:
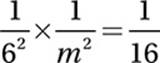
Multiply by m2:
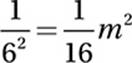
Multiply by 16:
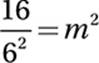
Simplify:
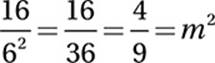
16. B
Data Analysis (probability) MEDIUM
Let R = the number of red marbles, W = the number of white marbles, and B = the number of blue marbles. If the jar contains twice as many red marbles as white marbles, then R = 2W. If the jar contains three times as many white marbles as blue marbles, then W = 3B. We can substitute numbers to these equations to solve the problem. Let’s say B = 10. This means there are 3(10) = 30 white marbles and 2(30) = 60 red marbles. The total number of marbles is therefore 10 + 30 + 60 = 100, and the number of non-red marbles is therefore 10 + 30 = 40 marbles, so the probability that the marble is not red is 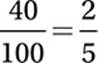 .
.
17. C
Advanced Mathematics (parabolas) MEDIUM
The vertex of a parabola with the equation y = A(x − h)2 + k is (h, k). For this parabola, h = 2 and k = 2. So, the vertex is (2, 2). The slope of the line that passes through (1, −3) and (2, 2) is
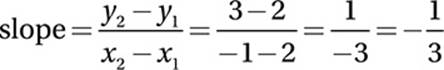
18. C
Advanced Mathematics (functions) MEDIUM-HARD
Let the input number be 7.
Step 1: Multiply the input value by 6:
42
Step 2: Add x to that result:
42 + x
Step 3: Divide this result by 4:
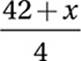
This must yield an output of 15:
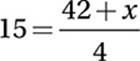
Multiply by 4:
60 = 42 + x
Subtract 42:
18 = x
19. C
Data Analysis (graphing data) MEDIUM-HARD
The graph of the quadratic y = ax2 + bx + c is a parabola. If a < 0, the parabola is “open-down” like a frowny-face. The only graph with this feature is (C).
20. B
Algebra (expressing relationships) MEDIUM-HARD
Draw a number line, and to show that p < r, place p to the left of r on the number line. The points that are closer to p than to r are all the points to the left of their midpoint. The midpoint is the average of the endpoints: 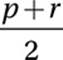 , so if the point with coordinate x is closer to p than to r, then
, so if the point with coordinate x is closer to p than to r, then 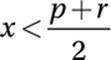 .
.
21. A
Algebra (simplifying expressions) MEDIUM-HARD
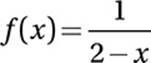
Substitute ![]() for x:
for x:
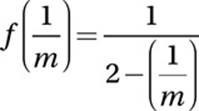
Simplify the denominator:
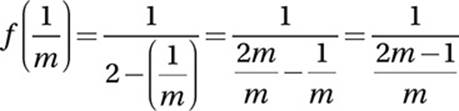
Divide by multiplying by the reciprocal:
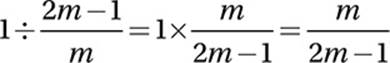
22. A
Advanced Mathematics (quadratics) MEDIUM-HARD
The graph of y = a(x − 2)(x + 1) is a quadratic with zeros (x-intercepts) at x = 2 and x = −1. The axis of symmetry of this parabola is halfway between the zeros, at x = (2 + −1)/2 = 1/2. Since a < 0, the parabola is “open down,” and so we have a general picture like this:
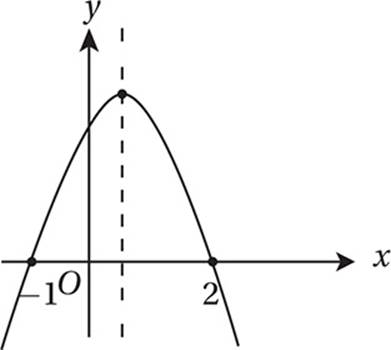
If you trace the curve from x = 0 to x = 5, that is, from the y-intercept and then to the right, you can see that the graph goes up a bit (until x = 1/2), and then goes down again.
Alternately, you can pick a negative value for a (like − 2) and graph the equation on your calculator.
23. D
Advanced Mathematics (rational equations) HARD
Given equation:
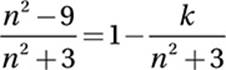
Add  :
:
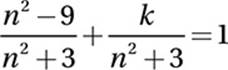
Combine the fractions into one:
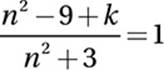
Multiply by n2 + 3:
n2 − 9 + k = n2 + 3
Subtract n2 :
−9 + k = 3
Add 9:
k = 12
24. C
Problem Solving (percentages) MEDIUM-HARD
Let p = the price per share of the stock. The cost of 200 of these shares (before commission) is therefore 200p. With a 3% commission, the cost becomes (1.03)(200p)
(1.03)(200p) = $3,399
Divide by 1.03:
200p = $3,300
Divide by 200:
p = $16.50 per share
25. A
Algebra (expressing quantities) MEDIUM-HARD
It may be easiest to choose number for w and y. Assume y = 4. If w is 50% greater than y, then w = 1.5(4) = 6. Therefore w−2 = 6−2 = 1/36, and y−2 = 4−2 = 1/16. Therefore the ratio of w−2 to y−2 is
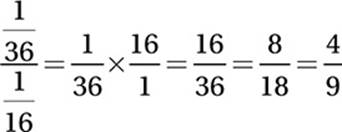
26. D
Data Analysis (set relations) HARD
Let’s let s = the total number of athletes in the group who play soccer, and t = the number of athletes in the group who run track. We can set up a Venn diagram to show the relationship between these two overlapping sets.
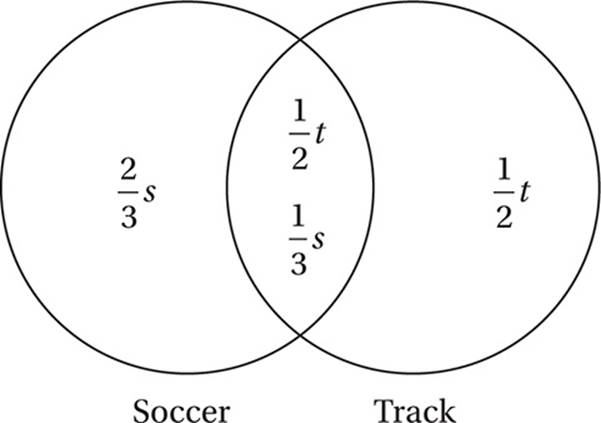
Since one-third of the soccer players also run track, we must put ![]() s in the overlapping region between soccer and track, and therefore the number who play only soccer is
s in the overlapping region between soccer and track, and therefore the number who play only soccer is ![]() s. Likewise, since one-half of the athletes who run track also play soccer, we must put
s. Likewise, since one-half of the athletes who run track also play soccer, we must put ![]() t in the overlapping region, and therefore the number of athletes who only run track is
t in the overlapping region, and therefore the number of athletes who only run track is ![]() t.
t.
Sincer there are 60 athletes in total:
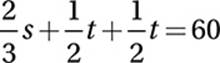
Simplify:
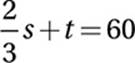
Multiply by 3 to simplify:
2s + 3t = 180
The number of soccer players who run track must equal the number of track athletes who play soccer:
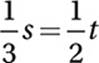
Multiply by 6 (the common denominator):
2s = 3t
Substitute 2s = 3t into the previous equation:
3t + 3t = 180
Simplify:
6t = 180
Divide by 6:
t = 30
Substitute t = 30 into the other
equation to solve for s:
2s = 3(30)
Simplify:
2s = 90
Divide by 2:
s = 45
Now we can use these values to complete the Venn diagram:
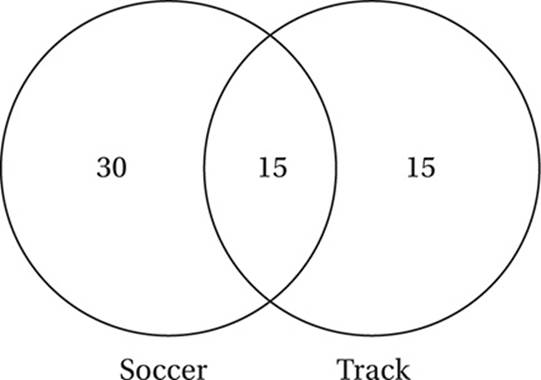
From this diagram, we can see that the only true statement among the choices is (D).
27. D
Advanced Mathematics (transformations) HARD
The graph of y = g(x) = f(x) + b is the graph of f vertically shifted up by b units. If g(x) = 0 has exactly one solution, the graph of y = g(x) can touch the x-axis at only one point: the vertex. Since the vertex of f has a y-coordinate of −2, this can only happen if f is shifted up 2 units, so b = 2.
28. B
Special Topics (trigonometry) HARD
The statement 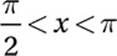 indicates that x is an angle in quadrant II, where the cosine is negative. Let’s draw this situation on the unit circle so we can visualize it. (We don’t want to confuse the angles called x and y in the problem with the x-coordinates and y-coordinates in the xy-plane. For this reason, let’s label the terminal rays for the angles “angle x” and “angle y.”) Recall that the cosine of any angle is the x-coordinate of the point on the unit circle that corresponds to that angle. If cos x = a, then a is the x-coordinate of the point on the unit circle that corresponds to “angle x,” as shown in the diagram.
indicates that x is an angle in quadrant II, where the cosine is negative. Let’s draw this situation on the unit circle so we can visualize it. (We don’t want to confuse the angles called x and y in the problem with the x-coordinates and y-coordinates in the xy-plane. For this reason, let’s label the terminal rays for the angles “angle x” and “angle y.”) Recall that the cosine of any angle is the x-coordinate of the point on the unit circle that corresponds to that angle. If cos x = a, then a is the x-coordinate of the point on the unit circle that corresponds to “angle x,” as shown in the diagram.
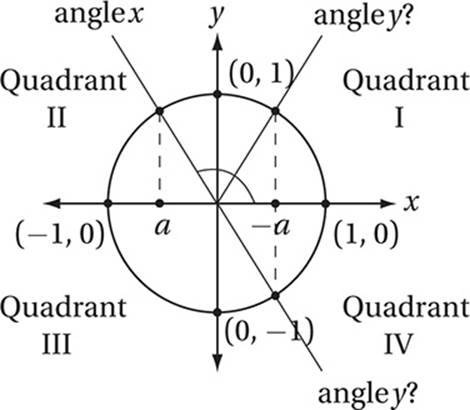
Now notice that, since a is a negative number, −a (that, is, the opposite of a), is a positive number. More specifically, it is the reflection of the point labeled a over the x-axis, as shown in the diagram. Now, if cos y = −a, then “angle y” corresponds to a point on the unit circle with an x-coordinate of −a. There are two possible locations for this point on the circle, and both are shown in the diagram above. Notice that one of these angles is the reflection of “angle x” over the y-axis. This is the supplement of “angle x,” that is, π − x. The other is the reflection of “angle x” over the origin, that is x + π. Therefore, the correct answer is (B).
Alternately, we could use the calculator to solve this problem by process of elimination. We can choose a value of “angle x” between π/2 and π. (In radian mode this is an angle between 1.57 and 3.14, and in degree mode it is an angle between 90° and 180°.) Let’s pick “angle x” to be 2 radians (about 115°). According to the calculator, cos(2) = −.416. Therefore, cos y must equal .416. Now we can substitute x = 2 into all of the choices and see which angle has a cosine of .416.
(A) cos(2 + 2π ) = −.416
(B) cos(2 + π) = .416
(C) cos(2 + π/2) = −.909
(D) cos(−2 + 2π) = −.416
Therefore the correct answer is (B).
29. A
Data Analysis (table) HARD
Since the question asks about those “who expressed an opinion on Proposal 81a,” we must ignore those who are listed as having No Opinion.
The number at the bottom right of the table indicated that there were 4,407 total people surveyed. But 719 of those had No Opinion, so 4,407 − 719 = 3,688 did have an opinion. What percentage of those are under 40? The answer is in the first row of the table (18 to 39): 917 of these Approve and 204 of these Disapprove. Therefore 917 + 204 = 1,121 of those showing an opinion are under 40 years of age.
Therefore the percentage of those showing an opinion who are under 40 is 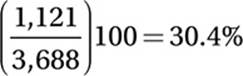
30. B
Data Analysis (table) HARD
(A) The approval rate for Proposal 81a generally decreases with the age of the voter.
Age 18 to 39:
918 out of 1,624 approve (56%)
Age 40 to 64:
1,040 out of 1,644 approve (64%)
Age 65 and older:
604 out of 1,139 approve (53%)
The approval rate increases and then decreases with age, so (A) is not correct.
(B) The disapproval rate for Proposal 81a generally increases with the age of the voter:
Age 18 to 39:
204 out of 1,624 disapprove (13%)
Age 40 to 64:
502 out of 1,644 disapprove (31%)
Age 65 and older:
420 out of 1,139 disapprove (37%)
The disapproval rate INCREASES as age increases, therefore (B) is correct.
31. 1/5 or 0.2
Data Analysis (variation) MEDIUM
If y varies inversely as x:
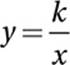
Substitute ½ = y and 10 = x:
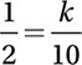
Cross multiply:
10 = 2k
Divide by 2:
5 = k
Therefore the general equation is:
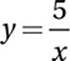
Substitute 25 = y:
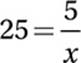
Multiply by x:
25x = 5
Divide by 25:
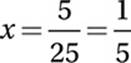
32. 169
Advance Mathematics (quadratics) MEDIUM
x2 = 12x = 13
Subtract 13:
x2 + 12x − 13 = 0
Factor:
(x + 13)(x − 1) = 0
Use the Zero Product Property:
x = −13 or x = 1
If x < 0, x must be −13. Therefore x2 = (−13)2 = 169.
Alternately, if you have QUADFORM (a quadratic formula program) programmed into your calculator, select PROGRAM, QUADFORM, and input a = 1, b = 12 and c = −13 to find the zeros (−13 and 1).
33. 112
Special Topics (polygons) MEDIUM-HARD
Notice that the “cutouts” can be reassembled to form two squares with side x and diagonal y, leaving an octagon with perimeter 8y.
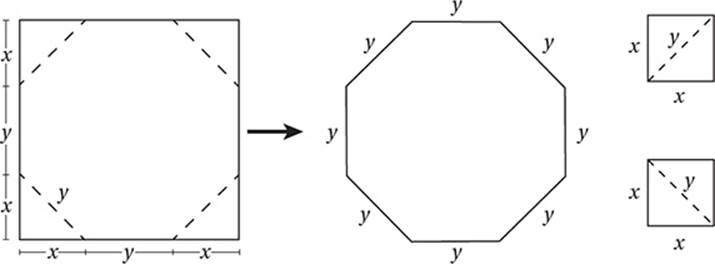
Since each of the cutout triangles is a right triangle:
x2 + x2 = y2
Simplify:
2x2 = y2
If the total area of the “cutouts” is 196 square centimeters:
2x2 = 196
Substitute 2x2 = y2:
y2 = 196
Take square root:
y = 14
Therefore the perimeter of the octagon is 8 × 14 = 112.
34. 16
Algebra (solving equations) HARD
Because m2 + n2 = 40, where m and n are both integers, we must look for two perfect squares that have a sum of 40. The perfect squares are 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 … and the only two of these with a sum of 40 are 4 and 36. So either m2 = 4 and n2 = 36 or m2 = 36 and n2 = 4.
CASE 1:
m2 = 4 and n2 = 36
Take square root:
m = ±2 and n = ±6
Since m < 0 < n:
m = −2 and n = 6
Evaluate (m + n)2:
(m + n)2 = (−2 + 6)2 = 42 = 16
CASE 2:
m2 = 36 and n2 = 4
Take square root:
m = ±6 and n = ±2
Since m < 0 < n:
m = −6 and n = 2
Evaluate (m + n)2:
(m + n)2 = (−6 + 2)2 = (−4)2 = 16
35. 1.4
Advanced Mathematics (trigonometry) MEDIUM-HARD
Recall the Pythagorean Trigonometric Identity, which is true for all x:
sin2 x + cos2 x = 1
Expression to be evaluated:
(sin x + cos x)2
FOIL:
(sin x + cos x)(sin x + cos x) = sin2 x + 2(sin x)(cos x) + cos2 x
Rearrange with Commutative and Associative Laws of Addition:
2(sin x)(cos x) + (sin2 x + cos2 x)
Substitute sin2 x + cos2 x = 1:
2(sin x)(cos x) + 1
Substitute (sin x)(cos x) = 0.2:
2(0.2) + 1 = 1.4
36. 115
Data Analysis (central tendency) MEDIUM
Begin by putting the data in order from least expensive to most expensive:
80 phones sold for $98
40 phones sold for $110
20 phones sold for $120
62 phones sold for $140
38 phones sold for $162
We don’t have to actually write out the prices of all 240 phones to find the median price. We can divide any set of 240 numbers, in ascending order, into two sets of 120 numbers. The median is in the middle of these, so it is the average of the 120th and 121st numbers. Since the first two categories account for 40 + 80 = 120 of these numbers, the 120th number in the set is $110, and the 121st number in the set is in the next higher category, $120. The median price is therefore ($110 + $120)/2 = $115.
37. 6.8
Problem Solving (extended thinking) HARD
If the height of the logo is to match the height of the banner, it must have a height of 4 feet. Let x be the corresponding length of the logo.
Since the logo has a height-to-length
ratio of 5:8:
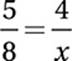
Cross multiply:
5x = 32
Divide by 5:
x = 6.4
Since the banner is 20 feet long, there are 20 - 6.4 = 13.6 feet in total for the side margins. If the logo is centered, then each margin is half this length, 13.6 ÷ 2 = 6.8 feet.
38. 25
Problem Solving (extended thinking) HARD
The banner has dimensions of 20 feet by 4 feet, so its area is 20 × 4 = 80 square feet. If the company charges $1.20 per square foot for the banner material, this cost is 80 × $1.20= $96. Based on the logo dimensions we determined in the previous problem, the area of the logo is 4 × 6.4 = 25.6 square feet. If the company charges $2.50 per square foot for the logo, the cost per printed logo is 25.6 × $2.50 = $64.
If the company charges a fixed cost of $32 per banner, then the total cost of a banner with ONE logo would be $96 + $64 + $32 = $192. The total cost of a banner with TWO logos would be $96 + $64 + $64 + $32 = $256.
We can calculate the percent savings with the “percent change” formula, since we are considering a “change” from the more expensive banner to the less expensive banner.
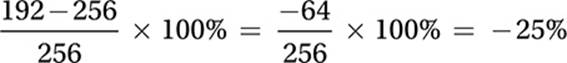
Therefore the percent savings is 25(%).
Section 5: Essay
Sample Response
Reading Score: 8 out of 8
Analysis Score: 8 out of 8
Writing Score: 8 out of 8
In this essay, Steven Pinker examines the “moral panics” surrounding new forms of media and the supposed cognitive and moral decline they cause. His essay provides a measure of balance to our modern discussions of social media and instantaneous digital information. He supports his thesis, that “such panics often fail reality checks,” with examples dating back as far as the 1950s, logical analysis, vibrant illustrative images, and touches of humor. He provides historical and scientific context for his claims and effectively encapsulates the broad misconceptions that cultural critics have about the relationship between modern media and the human brain. Although his argument could have been bolstered with more specific scientific support, his essay as a whole effectively argues for a reprieve from the hysteria about intellectual and moral decline allegedly caused by Twitter and Facebook.
Pinker makes use of “reductio ad absurdum,” or indirect proof, to make his case. This technique proceeds by arguing that if the point to be refuted were true, it would lead necessarily to a contradiction, and therefore it cannot be true. For instance, Pinker hints at this logical technique in the second paragraph: “When comic books were accused of turning juveniles into delinquents in the 1950s, crime was falling to record lows, just as the denunciations of video games in the 1990s coincided with the great American crime decline.” Here, Pinker is suggesting that sociological and psychological evidence refutes claims of social decline.
He uses reductio ad absurdum even more explicitly in the third paragraph: “If electronic media were hazardous to intelligence, the quality of science would be plummeting. Yet discoveries are multiplying like fruit flies, and progress is dizzying. Other activities in the life of the mind, like philosophy, history and cultural criticism, are likewise flourishing.” Unfortunately, Pinker does not provide substantial evidence to bolster these claims. He fails to address the common counterclaim that much of the “science” published on the Internet is flimsy, and the “cultural criticism” lazy.
Pinker then goes on to outline a basic lesson in human information processing, in an attempt to ground his argument in science. To Pinker, the claim that “information can change the brain” is facile (“it’s not as if the information is stored in the pancreas”) and misleading (“the existence of neural plasticity does not mean the brain is a blob of clay pounded into shape by experience”). Rather, Pinker suggests, “the effects of experience are highly specific to the experiences themselves. … Music doesn’t make you better at math; conjugating Latin doesn’t make you more logical; brain-training games don’t make you smarter.” Unfortunately, Pinker here seems to mistake assertion for argumentation. He is directly contradicting the claims of thousands of music and Latin teachers, as well as dozens of Lumosity commercials. But he is only gainsaying. Here again, we might expect some data to support his points.
Next, Pinker attempts to refute cultural critics by drawing analogies between their reasoning and the faulty reasoning of “primitive peoples” who believe that “eating fierce animals will make them fierce.” He likens this to the thinking of modern observers who believe that “reading bullet points and Twitter postings turns your thoughts into bullet points and Twitter postings.” But of course just because one line of reasoning parallels another does not mean that both are equally incorrect. Here again, Pinker’s argument would benefit from information about the actual cognitive effects of reading Twitter feeds.
Next, Pinker provides a qualification: “Yes, the constant arrival of information packets can be distracting or addictive, especially to people with attention deficit disorder.” But here again, even in conceding a point, Pinker doesn’t quite offer the information a reader might want: How significant is this distraction or addiction, and does it have any harmful long-term effects? We don’t get this information from Pinker, but we do get some practical advice: “Turn off e-mail or Twitter when you work …” We get even more substantial advice in the next paragraph: to cultivate “intellectual depth,” we must avail ourselves of “special institutions, which we call universities” and engage in “analysis, criticism, and debate.” But why, a reader might wonder, should we moderate our use of electronic media if it doesn’t have any real harmful effects?
Finally, Pinker ends with a broader perspective and a note of hope: “the Internet and information technologies are helping us manage, search, and retrieve our collective intellectual output. … Far from making us stupid, these technologies are the only things that will keep us smart.” Perhaps Pinker is right, but his argument would be stronger with more substantial quantitative evidence and more direct refutation of our real concerns about how the Internet might be changing our brains.
Scoring
Reading—8 (both readers gave it a score of 4)
This response demonstrates extremely thorough comprehension of Pinker’s essay through skillful use of summary, paraphrase, and direct quotations. The author summarizes Pinker’s central thesis and modes of persuasion (His thesis, that “such panics often fail reality checks,” is supported with examples dating back as far as the 1950s, careful logical analysis, vibrant illustrative images, and touches of humor) and shows a clear understanding of Pinker’s supporting ideas and overall tone (He provides historical and scientific context for his claims and effectively encapsulates the broad misconceptions that cultural critics have about the relationship between modern media and the human brain. … Pinker ends with a broader perspective and a note of hope). Each quotation is accompanied by insightful commentary that demonstrates that this author thoroughly understands Pinker’s central and secondary ideas, and even recognizes when Pinker seems occasionally to fall short of his own purpose.
Analysis—8 (both readers gave it a score of 4)
This response provides a thoughtful and critical analysis of Pinker’s essay and demonstrates a sophisticated understanding of the analytical task. The author has identified Butler’s primary modes of expression (logical analysis, vibrant illustrative images, and touches of humor) and has even provided a detailed examination of Pinker’s preferred logical method, reductio ad absurdum, with a discussion of several examples. Perhaps even more impressively, the author indicates where Pinker’s evidence falls short, providing critical analysis and suggesting alternatives (Unfortunately, Pinker does not provide substantial evidence to bolster these claims. He doesn’t address the common counterclaim that much of the “science” published on the Internet is flimsy, and the “cultural criticism” lazy. … Pinker here seems to mistake assertion for argumentation. … Here again, Pinker’s argument would benefit from information about the actual cognitive effects of reading Twitter feeds). Overall, the author’s analysis of Pinker’s essays demonstrates a thorough understanding not only of the rhetorical task that Pinker has set for himself, but also the means by which it is best accomplished.
Writing—8 (both readers gave it a score of 4)
This response shows a masterful use of language, sentence structure to establish a clear and insightful central claim (Although his argument could have been bolstered with more specific scientific support, his essay as a whole effectively argues for a reprieve from the hysteria about intellectual and moral decline allegedly caused by Twitter and Facebook). The response maintains a consistent focus on this central claim and supports it with a well-developed and cohesive analysis of Pinker’s essay. The author demonstrates effective verb choice (effectively encapsulates the broad misconceptions. … He likens this to the thinking of modern observers), strong grasp of relevant analytical terms, like reduction ad absurdum, facile, sociological and psychological evidence, counterclaim, assertion, argumentation, and gainsaying. The response is well-developed, progressing from general claim to specific analysis to considered evaluation. Largely free from grammatical error, this response demonstrates strong command of language and proficiency in writing.