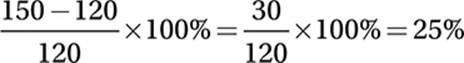SAT 2016
CHAPTER 7
THE SAT MATH TEST: THE HEART OF ALGEBRA
1. Working with Expressions
2. Working with Linear Equations
3. Working with Inequalities and Absolute Values
4. Working with Linear Systems

The SAT Math: Heart of Algebra
Why is algebra so important on the SAT Math test?
About 36% (21 out of 58) of the SAT Math questions fall under the category called the “Heart of Algebra.” Questions in this category test your ability to
analyze, fluently solve, and create linear equations, inequalities, [and] systems of equations using multiple techniques.
These questions will also assess your skill in
interpreting the interplay between graphical and algebraic representations [and] solving as a process of reasoning.
The specific topics include
• creating and solving linear equations in one and two variables
• graphing and interpreting linear equations
• creating, interpreting, and solving linear systems
• graphing and solving inequalities and systems of inequalities
• interpreting and solving algebraic word problems
Why are these skills important?
Algebra is an essential tool of quantitative analysis not only in math but also in subjects like engineering, the physical sciences, and economics. When describing the relationships between or among different quantities, or exploring the nature of unknown quantities, algebra provides essential tools for analyzing and solving problems. Most colleges consider fluency in algebra to be a vital prerequisite to a college-level liberal arts curriculum.
Sound intimidating? It”s not.
If you take the time to master the four core skills presented in these 13 lessons, you will gain the knowledge and practice you need to master even the toughest SAT Math “Heart of Algebra” questions.
Skill 1: Working with Expressions
Lesson 1: Using algebraic expressions
To solve tough SAT math problems, you must be fluent in defining, manipulating, and analyzing algebraic expressions.
Corrine drives to her office at an average speed of 50 miles per hour. When she returns home by the same route, the traffic is lighter and she averages 60 miles per hour. If her trip home is 10 minutes shorter than her trip to her office, what is the distance, in miles, from Corrine”s home to her office?

(Medium-hard) Why does everyone hate “word problems” like this one? For most of us, the problem is that the equations aren”t “set up” for us—we have to set them up ourselves, which can be a pain in the neck. But we can make these problems much easier by breaking them down into clear steps.
Key Steps to Solving Tough Algebraic Problems
Solving tough problems in mathematics and science frequently involves four essential steps:
1. identify the relevant quantities in the situation
2. express those quantities with algebraic expressions
3. translate the facts of the problem situation into equations involving those expressions
4. analyze and solve those equations
Step 1. Identify: In this problem, there are six relevant quantities:
• the speed from home to work
• the distance from home to work
• the time it takes to get from home to work
• the speed from work to home
• the distance from work to home
• the time it takes to get from work to home
This may seem like a lot, but as we will see, keeping track of them is quite manageable.
Step 2. Express: The problem gives us enough information to express all six quantities in terms of only two “unknowns.” If d is the distance, in miles, from her home to her office, and t is the time, in hours, it takes her to get home from the office, then we can express our six quantities, respectively, as

Step 3. Translate: To translate the facts of this problem into equations, we must know the formula distance = average speed × time. Applying this to each trip gives us

Step 4. Analyze and Solve: We have now reduced the problem to a “two by two system,” that is, two equations with two unknowns. Since the number of equations equals the number of unknowns, we should be able to solve for those unknowns. (In Lessons 12 and 13, we will review these concepts and techniques.) Since the unknown d is isolated in both equations, substitution is simple:

Since t represents the time it took Corrine to return home, in hours, this means it took her 5/6 hours (or 50 minutes) to get from her office to her home, and 5/6 hour + 1/6 hour = 1 hour to get to her office from home. But remember, the question asks for the distance from her home to her office, which we can find by substituting into either of our equations:
50(5/6 + 1/6) or 60(5/6) = 50 miles
Lesson 2: The Laws of Arithmetic
When expressing or simplifying a quantity, you frequently have many options. For instance, the expression 4x2 – 12x can also be expressed as 4x(x – 3). Similarly, 3.2 can be expressed as 16/5 or 3 ⅕ or 32/10. Which way is better? It depends on what you want to do with the expression. Different forms of an expression can reveal different characteristics of that quantity or the equation in which it appears. To gain fluency in expressing quantities, you must understand the Laws of Arithmetic.


To simplify complex expressions, you must know the Order of Operations:
PG-ER-MD-AS
Step 1: PG (parentheses and other grouping symbols, from innermost to outermost and left to right)
Since this expression contains no parentheses, we don”t have to worry about “grouped” operations, right? Wrong! Remember that fraction bars and radicals are “grouping symbols” just like parentheses are.
In other words, we can think of this expression as
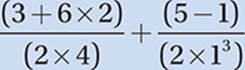
If a set of parentheses contains only one operation, then we simply do that operation:
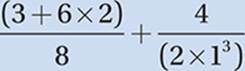
If it contains more than one operation, then we must move on to the next step.
Step 2: ER (exponents and roots, from innermost to outermost and left to right)
Do any of the parentheses contain exponents or roots? Yes, so we must perform that operation next:
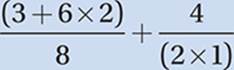
Step 3: MD (multiplication and division, from left to right)
Next, we do any multiplication inside the parentheses:
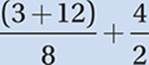
Step 4: AS (addition and subtraction, from left to right)
Now we do any addition and subtraction left in the parentheses:
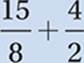
Once all the “grouped” operations are completed, we run through the order of operations once again to finish up. Exponents or roots? No. Multiplication or division? Yes:
1.875 + 2
Addition or subtraction? Yes: 1.875 + 2 = 3.875
What is the sum of the first 100 positive integers?

(Hard) Here, following the order of operations would be, shall we say, less than convenient: it would require 99 computations. Even with a calculator, it would be a pain. But here is a much simpler method:
Original expression:
1 + 2 + 3 + 4 + … + 97 + 98 + 99 + 100
Rearrange and regroup:
(1 + 100) + (2 + 99) + (3 + 98) + … + (50 + 51)
Simplify:
(101) + (101) + (101) + … + (101)
Since we have 50 pairs, this equals:
50(101)
Simplify:
5,050
This gives us exactly the same result as the order of operations would give, but with just a few simple calculations. How did we do it? By using three more laws of arithmetic: the commutative law of addition, the associative law of addition, and the distributive law of multiplication over addition.
Use the Laws of Arithmetic to simplify expressions or reveal their properties.
The Commutative Law of Addition
When adding, order doesn”t matter.
e.g., 3 + 8 + 17 + 12 = 3 + 17 + 12 + 8
The Commutative Law of Multiplication
When multiplying, order doesn”t matter.
e.g., 2 × 16 × 50 × 3 = 3 × 16 × 50 × 2
The Associative Law of Addition
When adding, grouping doesn”t matter.
e.g., 1 + 100 + 2 + 99 + 3 + 98 + … + 50 + 51 = (1 + 100) + (2 + 99) + (3 + 98) + … + (50 + 51)
The Associative Law of Multiplication
When multiplying, grouping doesn”t matter.
e.g., 1 × 2 × 3 × 4 × 5 = (1 × 2 × 3) × (4 × 5)
The Distributive Law of Multiplication over Addition
When multiplying by a grouped sum, you don”t have to do the grouped sum first; you can multiply first, as long as you distribute the multiplication over the entire sum.
e.g., 5(20 + 7) = 5 × 20 + 5 × 7 = 100 + 35 = 135
Which of the following is equivalent to 3(34 × 53)? [No calculator]
A) 3(34) × 3(53)
B) 94 + 153
C) 94 × 153
D) 35 × 53
Before making your choice, check the laws of arithmetic; don”t make up your own laws. Which laws of arithmetic can we use? Since the expression is a product, we can use the commutative law of multiplication and jumble up the terms, or the associative law of multiplication and regroup the terms any way we want (or not at all). Using the associative law gives us
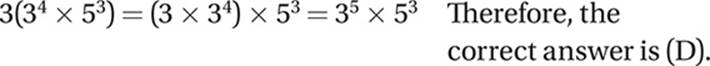
Don”t “over-distribute.”
Were you tempted to choose (A), (B), or (C) in the question above? If so, you are not alone. You are simply the victim of one of the most common mistakes in algebra: over-distribution. It comes from a misinterpretation of the Law of Distribution. The correct law is
When multiplying by a grouped sum, you don”t have to do the grouped sum first; you can multiply first, as long as you distribute the multiplication over the entire sum.
It is not
If something is outside parentheses, just bring it inside and distribute.
Look at these examples of “over-distribution” and verify that they are incorrect:
3(2 × 5) is not equal to (3 × 2) + (3 × 5) or (3 × 2) × (3 × 5)
(2 + 3)2 is not equal to 22 + 32
If x ≠ 0, which of the following equals 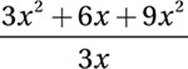 ?
?
A) 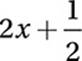
B) 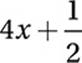
C) 2x2 + 2
D) 4x + 2
(Medium)
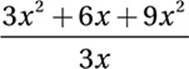
Commutative Law of Addition:
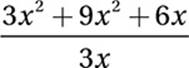
Associative Law of Addition:
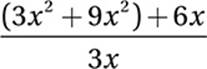
Distributive Law:
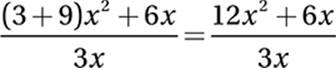
Division by a number is multiplication by its reciprocal:
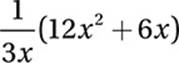
Distributive Law:
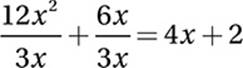
So the correct answer is (D). Look at each step carefully and notice how each one uses a particular Law of Arithmetic. In particular, notice that the “combining of like terms” in steps 1–3 is really an example of commuting, associating, and (un)distributing. Even more interesting, notice that steps 4–5 show that division distributes just like multiplication does.
You can also distribute division over addition just as you can distribute multiplication.
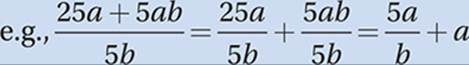
How many distinct values of x are solutions to the equation x2 + 4 = −4x?
A) none
B) one
C) two
D) three
(Medium) You might recognize that this equation is a quadratic equation (which we will discuss in much more detail in Chapter 9) and remember that such equations usually have two distinct solutions, but not always, so we must look at this equation more carefully.

Step 2 might seem a bit mysterious. Why did we write 4x as 2x + 2x? Here we are using the Product-Sum Method for factoring quadratics, which is explained in a bit more detail in Chapter 9, Lesson 4. For now, though, just notice that each step follows a particular Law of Arithmetic.
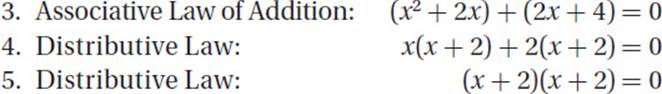
If the product of two numbers is 0, then one of those numbers must be 0. (This is the Zero Product Property.) Therefore x + 2 = 0 and so x = −2. Since the other factor is the same, we only get one solution to this equation, and the answer is (B).
To check the equation in step 5, we can FOIL the product of binomials on the left side to make sure we get the same expression we had back in step 1: (x + 2)(x + 2) = x2 + 4x + 4, which is precisely the expression we started with in step 1, confirming that our work is correct.
This means that the factoring process in steps 2–5 can be thought of as un-FOILing. We will look at this method of factoring more carefully in Chapter 9.
Make sure you know how to FOIL and un-FOIL.
FOILing is simply the shortcut for multiplying two binomials, which requires applying the distributive law twice. For example:

Exercise Set 1 (No Calculator)
1
(1 − (1 − (1 − 2))) − (1 − (1 − (1 − 3))) =

2
When 14 is subtracted from 6 times a number, 40 is left. What is half the number?

3
Four consecutive even numbers have a sum of 76. What is the greatest of these numbers?

4
If 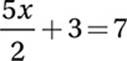 , then 10x + 12 =
, then 10x + 12 =

5
What number decreased by 7 equals the opposite of five times the number?

6
If 5d + 12 = 24, then 5d − 12 =

7
If 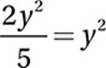 , then y + 5 =
, then y + 5 =

8
The product of x and y is 36. If both x and y are integers, then what is the least possible value of x − y?
A) −37
B) −36
C) −35
D) −9
9
If a factory can manufacture b computer screens in n days at a cost of c dollars per screen, then which of the following represents the total cost, in dollars, of the computer screens that can be manufactured, at that rate, in m days?
A) 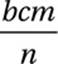
B) 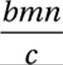
C) ![]()
D) ![]()
10
Which of the following is equivalent to 5x(2x × 3) − 5x2 for all real values of x?
A) 5x2 + 15x
B) 25x2
C) 5x2 − 15x
D) 10x2 × 15x − 5x2
11
The symbol Ο represents one of the fundamental operators: +, −, ×, or ÷. If (x Ο y) × (y Ο x) = 1 for all positive values of x and y, then Ο can represent
A) +
B) ×
C) −
D) ÷
Exercise Set 1 (Calculator)
12
The difference of two numbers is 4 and their sum is 14. What is their product?

13
If x + y − 1 = 1 − (1 − x), what is the value of y?

14
If 3x2 + 2x = 40, then 15x2 + 10x =

15
Ellen is currently twice as old as Maria, but in 6 years, Maria will be 2/3 as old as Ellen. How old is Ellen now?

16
If 2x − 2y = 5 and x + y = 6, what is the value of x2 − y2?

17
On a typical day, a restaurant sells n grilled cheese sandwiches for p dollars each. Today, however, the manager reduced the price of grilled cheese sandwiches by 30% and as a result sold 50% more of them than usual. Which of the following represents the revenue for today”s grilled cheese sandwich sales, in dollars?
A) 0.5np − 0.3
B) 1.05np
C) 1.20np
D) 1.50np
18
For all real numbers x and y, 4x(x) − 3xy(2x) =
A) 12x2y(x − 2y)
B) 2x2(2 − 3y)
C) 2x2(2 + 3y)
D) 4xy(x − 3y)
19
If a = 60(99)99 + 30(99)99, b = 99100, and c = 90(90)99, then which of the following expresses the correct ordering of a, b, and c?
A) c < b < a
B) b < c < a
C) a < b < c
D) c < a < b
20
Which of the following statements must be true for all values of x, y, and z?
I. (x + y) + z = (z + y) + x
II. (x − y) − z = (z − y) − x
III. (x ÷ y) ÷ z = (z ÷ y) ÷ x
A) I only
B) I and II only
C) I and III only
D) II and III only
21
Carlos began with twice as much money as David had. After Carlos gave $12 to David, Carlos still had $10 more than David. How much money did they have combined at the start?
A) $34
B) $68
C) $102
D) $108
EXERCISE SET 1 ANSWER KEY
No Calculator
1. 1
(1 − (1 − (1 − 2))) − (1 − (1 − (1 − 3)))
Parentheses:
(1 − (1 − (−1))) − (1− (1 − (−2)))
Next parentheses:
(1 − (2)) − (1 − (3))
Next parentheses:
(−1) − (−2)
Subtract:
−1 + 2 = 1
2. 9/2 or 4.5
6x − 14 = 40
Add 14:
6x = 54
Divide by 6:
x = 9
Multiply by ![]() :
:
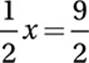
3. 22 Let n be the least of these numbers. The sum of four consecutive even numbers is therefore n + (n + 2) + (n + 4) + (n + 6) = 76.
Simplify:
4n + 12 = 76
Subtract 12:
4n = 64
Divide by 4:
n = 16
Therefore the largest of these numbers is 16 + 6 = 22.
4. 28
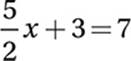
Multiply by 4:
10x + 12 = 28
5. 7/6 or 1.16 or 1.17
x − 7 = −5x
Subtract x:
−7 = −6x
Divide by –6:
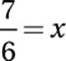
6. 0
5d + 12 = 24
Subtract 24:
5d − 12 = 0
7. 5
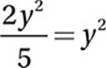
Subtract y2:
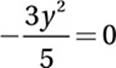
Multiply by −5/3:
y2 = 0
Take square root:
y = 0
Add 5:
y + 5 = 5
8. C If xy = 36 and x and y are integers, then x and y are both factors of 36. In order to minimize the value of x − y, we must find the greatest separation between x and y. The greatest separation between a factor pair is 1 − 36 = −35.
9. A We should regard this as a “conversion” problem from m days into a corresponding number of dollars.
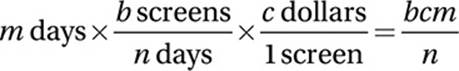
10. B Original expression:
5x(2x × 3) − 5x2
Parentheses:
5x(6x) − 5x2
Multiply:
30x2 − 5x2
Subtract:
25x2
Remember: The Law of Distribution does not apply in the first step, because the grouped expression doesn”t include addition or subtraction.
11. D The simplest approach is perhaps to choose simple values for x and y, like 2 and 3, and see which operator yields a true equation. Since (2 ÷ 3) × (3 ÷ 2) = 1, the answer is (D).
Calculator
12. 45
a − b = 4
a + b = 14
Add equations:
2a = 18
Divide by 2:
a = 9
Substitute a = 9:
9 + b = 14
Subtract 9:
b = 5
Evaluate ab:
ab = 9 × 5 = 45
13. 1
x + y − 1 = 1 − (1 − x)
Distribute:
x + y − 1 = 1 − 1 + x
Subtract x:
y − 1 = 1 − 1
Simplify:
y − 1 = 0
Add 1:
y = 1
14. 200
3x2 + 2x = 40
Multiply by 5:
15x2 + 10x = 200
15. 12 Let e = Ellen”s current age and m = Maria”s current age.
Ellen is twice as old as Maria:
e = 2m
In 6 years, Maria will be 2/3 as old as Ellen:
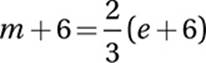
Substitute e = 2m:
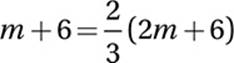
Multiply by 3:
3m + 18 = 2(2m + 6)
Distribute:
3m + 18 = 4m + 12
Subtract 3m and 12:
6 = m
Therefore e = 2m = 2(6) = 12.
16. 15 First equation:
2x − 2y = 5
Divide by 2:
x − y = 2.5
Second equation:
x + y = 6
Multiply:
(x − y)(x + y) = x2 − y2 = (2.5)(6) = 15
Alternately, we could solve the system using either substitution or linear combination and get x = 4.25 and y = 1.75, and evaluate x2 − y2 = (4.25)2 − (1.75)2 = 18.0625 − 3.0625 = 15.
17. B The revenue is equal to the number of items sold times the price per item. If the restaurant typically sells n sandwiches per day, but today sold 50% more, it sold 1.5n sandwiches. If the price p was reduced 30%, today”s price is 0.70p. Therefore, the total revenue is (1.5n)(0.70p) = 1.05np.
18. B
4x(x) − 3xy(2x)
Multiply:
4x2 − 6x2y
Largest common factor:
2x2(2 − 3y)
19. D Although a calculator is permitted for this question, most calculators will give an “overflow error” when trying to calculate numbers like 99100, because they”re just too large. However, comparing these numbers is straightforward if we can express them in a common format.

20. A Only statement I is true, by the Commutative and Associative Laws of Addition. Choosing simple values like x = 1, y = 2, and z = 3 will demonstrate that statements II and III do not yield true equations.
21. C Let x = the number of dollars David had to start. If Carlos started with twice as much money as David, then Carlos started with 2x dollars. After Carlos gave David $12, Carlos had 2x − 12 dollars and David had x + 12 dollars. If Carlos still had $10 more than David, then
2x − 12 = 10 + x + 12
Simplify:
2x − 12 = x + 22
Add 12:
2x = x + 34
Subtract x:
x = 34
Therefore, David started with $34 and Carlos started with 2($34) = $68, so they had $34 + $68 = $102 combined to start.
Lesson 3: Simplifying expressions and operations
If x and y are positive numbers and 3x − 2y = 7, what is the value of 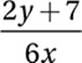 ?
?
A) ![]()
B) ![]()
C) ![]()
D) ![]()
(Easy) Working with algebraic equations doesn”t always mean “solving for x.” Notice that this particular question doesn”t ask for the values of x or y, but rather for the value of a more complicated expression. This may seem harder, but it”s actually pretty simple if you understand the Law of Substitution
The Law of Substitution
If two expressions are equal, then you may substitute one for the other at any point in the problem.
How does this help us here? Notice that if we simply add 2y to both sides of the equation, we get
3x − 2y = 7
Add 2y:
3x = 2y + 7
Therefore, by the Law of Substitution, we can substitute 3x for 2y + 7 or vice-versa. Since 2y + 7 appears in the expression we are asked to evaluate, it makes sense to replace it with 3x:
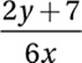
Substitute 3x for 2y + 7:
![]()
Simplify:
![]()
When a question asks you to analyze a complex expression, don”t be intimidated. Look for simple relationships that allow you to simplify them using techniques like the Law of Substitution.
Increasing a positive number x by 25% and then decreasing the result by 50% is equivalent to dividing x by what number?
A) 1.333
B) 1.5
C) 1.6
D) 1.625
(Medium) Increasing a quantity by 25% is equivalent to multiplying it by 1.25, because the final amount is 125% of the original amount (Chapter 8, Lesson 8). Decreasing a quantity by 50% is equivalent to multiplying it by .5, because the final amount is 50% of the original amount. Therefore, performing both changes is equivalent to multiplying by 1.25 × 0.50, or 0.625, which is equal to 5/8. But the question asks us for the equivalent division. Here, we need to remember a simple rule: multiplying by a number is equivalent to dividing by its reciprocal. Therefore, multiplying by 5/8 is the same as dividing by 8/5, which is 1.6. Therefore, the correct answer is (C).
Every operation can be expressed in terms of its inverse operation.

And here are two more handy equivalences:

If 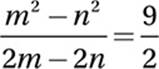 what is the value of m + n?
what is the value of m + n?

(Easy) When a problem includes a complicated expression, we should try to simplify it, but always keep an eye on what the question is asking. In this case, simplifying to find the value of m + n requires knowing some factoring identities.
Useful factoring identities
The difference of squares equals the product of conjugates:
x2 − y2 = (x + y)(x − y)
Perfect square polynomials:
x2 + 2ax + a2 = (x + a)(x + a)
x2 − 2ax + a2 = (x − a)(x − a)
The first of these identities helps us factor our numerator:
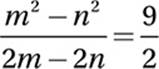
Factor numerator and denominator:
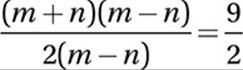
Cancel common factors:
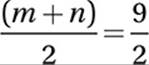
Multiply by 2:
m + n = 9
Lesson 4: Using conversion as a problem-solving tool
Niko is 27 inches shorter than his father, who is 5 feet 10 inches tall. How tall is Niko? (1 foot = 12 inches)
A) 3 feet 4 inches
B) 3 feet 6 inches
C) 3 feet 7 inches
D) 3 feet 10 inches
(Easy) Solving this problem requires unit conversions. To convert inches to feet, we multiply by the conversion factor (1 foot/12 inches). To convert feet to inches, we multiply by its reciprocal (12 inches/1 foot). If Niko”s father is 5 feet 10 inches tall, he is 5 feet × (12 inches/1 foot) + 10 inches = 70 inches tall. If Niko is 27 inches shorter, he is 70 − 27 = 43 inches tall, which is equivalent to 43 inches × (1 foot/12 inches) = 3 7/12 feet, or 3 feet 7 inches, so the correct answer is (C).
Conversion factors as problem-solving tools
A conversion factor is simply a fraction in which the quantities in the numerator and the denominator represent equal quantities. Sometimes the equivalence is universal—for instance, 1 pound is always equal to 16 ounces—and sometimes it is problem-specific—for instance when a machine pump waters at a rate 3 gallons per hour, 1 hour of pumping is “equal” to 3 gallons being pumped.
If a factory can manufacture b computer screens in n days at a cost of c dollars per screen, then which of the following represents the total cost, in dollars, of the computer screens that can be manufactured, at that rate, in m days?
A) 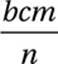
B) 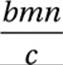
C) ![]()
D) ![]()
(Medium) This problem, from the previous exercise set, can be solved in several different ways. One method is to simply choose values for the unknowns and turn the problem into an arithmetic problem instead of an algebra problem. But here we will look at it as a conversion problem.
We can think of this problem as being a “conversion” from a quantity of days to an equivalent quantity of dollars. We are given that this factory is working for m days, so we write this quantity down, including the units, and we multiply by the conversion factors until we get dollars:
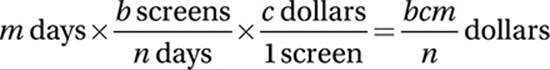
So the correct answer is (A).
Exercise Set 2 (No Calculator)
1
If bag A weighs 4 pounds 5 ounces and bag B weighs 6 pounds 2 ounces, how much heavier, in ounces, is bag B than bag A? (1 pound = 16 ounces)

2
If 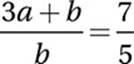 , what is the value of
, what is the value of ![]() ?
?

3
If x − 2y = 10 and x ≠ 0, what is the value of 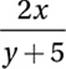 ?
?

4
If a − b = 4 and a2 − b2 = 3, what is the value of a + b?

5
If 6 gricks are equivalent to 5 merts, then 2 merts are equivalent to how many gricks?

6
If the function {x} is defined by the equation {x} = (1 − x)2, what is the value of {{4}}?

7
If 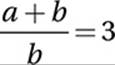 and
and 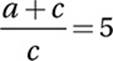 , what is the value of
, what is the value of ![]() ?
?

8
(x − 9)(x − a) = x2 − 4ax + b
In the equation above, a and b are constants. If the equation is true for all values of x, what is the value of b?
A) −27
B) −12
C) 12
D) 27
9
If 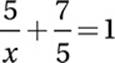 , what is the value of x?
, what is the value of x?
A) 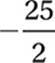
B) −7
C) 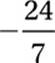
D) ![]()
10
(p + 2)2 = (p − 5)2
The equation above is true for which of the following values of p?
A) −2 and 5
B) 2 and −5
C) 1.5 only
D) 5 only
11
If 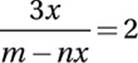 for all positive values of m and n, then which of the following is equal to x?
for all positive values of m and n, then which of the following is equal to x?
A) 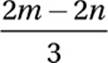
B) 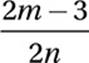
C) 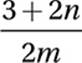
D) 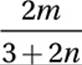
Exercise Set 2 (Calculator)
12
Let m be a positive real number. Increasing m by 60% then decreasing the result by 50% is equivalent to dividing m by what number?

13
What is the sum of the first 50 positive even integers?

14
Three years ago, Nora was half as old as Mary is now. If Mary is four years older than Nora, how old is Mary now?

15
If 2/3 of the seats at a football stadium were filled at the beginning of the game, and at halftime 1,000 spectators left, leaving 3/7 of the seats filled, what is the total number of seats in the stadium?

16
If three candy bars and two gumdrops cost $2.20, and four candy bars and two gumdrops cost $2.80, what is the cost, in dollars, of one gumdrop?

17
If 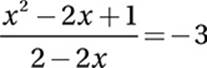 , what is the value of x −1?
, what is the value of x −1?

18
Subtracting 3 from a number and then multiplying this result by 4 is equivalent to multiplying the original number by 4 and then subtracting what number?

19
In a poker game, a blue chip is worth 2 dollars more than a red chip, and a red chip is worth 2 dollars more than a green chip. If 5 green chips are worth m dollars, then which of the following represents the value, in dollars, of 10 blue chips and 5 red chips?
A) 50 + 3m
B) 18 + 60m
C) 40 + 3m
D) 28 + 20m
20
A train travels at an average speed of 50 miles per hour for the first 100 miles of a 200-mile trip, and at an average of 75 miles per hour for final 100 miles. What is the train”s average speed for the entire trip?
A) 58.5 mph
B) 60.0 mph
C) 62.5 mph
D) 63.5 mph
21
Which of the following is equivalent to 3m(m2 × 2m) for all real values of m?
A) 3m2 + 6m
B) 3m2 × 6m
C) 3m3 × 6m2
D) 6m4
22
If the cost of living in a certain city increased by 20% in the 10 years from 1980 to 1990, and increased by 50% in the 20 years from 1980 to 2000, what was the percent increase in the cost of living from 1990 to 2000?
A) 15%
B) 20%
C) 25%
D) 30%
EXERCISE SET 2 ANSWER KEY
No Calculator
1. 29 4 pounds 5 ounces = 4(16) + 5 = 69 ounces, and 6 pounds 2 ounces = 6(16) + 2 = 98 ounces. Therefore, bag B weighs 98 − 69 = 29 ounces more.
2. 2/15 or .133
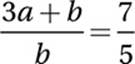
Distribute division:
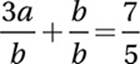
Simplify:
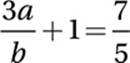
Subtract 1:
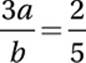
Divide by 3:
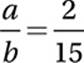
3. 4 Expression to be evaluated:
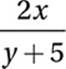
Given equation:
x − 2y = 10
Add 2y:
x = 2y + 10
Substitute x = 2y + 10:
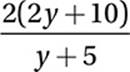
Simplify:
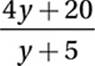
Factor and simplify:
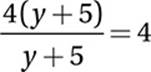
4. ¾ or .75
a2 − b2 = 3
Factor:
(a − b)(a + b) = 3
Substitute a − b = 4:
4(a + b) = 3
Divide by 4:
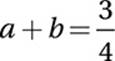
5. 12/5 or 2.4
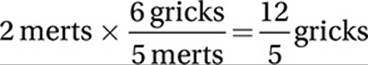
6. 64
{4} = (1 − 4)2 = (−3)2 = 9
{{4}} = (1 − {4})2 = (1 − 9)2 = (−8)2 = 64
7. 2 Given equation:
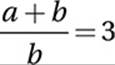
Distribute division:
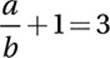
Subtract 1:
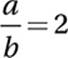
Reciprocate:
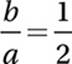
Given equation:
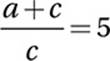
Distribute division:
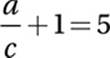
Subtract 1:
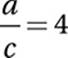
Multiply:
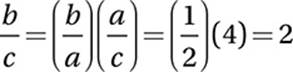
8. D Given:
(x − 9)(x − a) = x2 − 4ax + b
FOIL:
x2 − ax − 9x + 9a = x2 − 4ax + b
Simplify:
x2 − (a + 9)x + 9a = x2 − 4ax + b
If this equation is true for all x, then the coefficients of corresponding terms must be equal, so
a + 9 = 4a
Subtract a:
9 = 3a
Divide by 3:
3 = a
Therefore b = 9a = 9(3) = 27.
9. A Given equation:
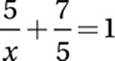
Multiply by 5x:
25 + 7x = 5x
Subtract 7x:
25 = −2x
Divide by −2:
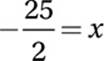
10. C Given equation:
(p + 2)2 = (p − 5)2
FOIL:
p2 + 4p + 4 = p2 − 10p + 25
Subtract p2:
4p + 4 = −10p + 25
Add 10p:
14p + 4 = 25
Subtract 4:
14p = 21
Divide by 14:
p = 1.5
11. D Given equation:
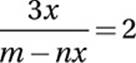
Multiply by m − nx:
3x = 2(m − nx)
Distribute:
3x = 2m − 2nx
Add 2nx:
3x + 2nx = 2m
Factor out x:
x(3 + 2n) = 2m
Divide by 3 + 2n:
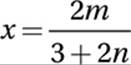
Calculator
12. 1.25 Increasing a number by 60% is equivalent to multiplying it by 1.60, and decreasing a number by 50% is equivalent to multiplying it by 0.50. Therefore, performing both changes in succession is equivalent to multiplying by 1.60 × 0.50 = 0.80. Multiplying by 0.80 is equivalent to dividing by its reciprocal: 1/(0.80) = 1.25.
13. 2,550 The sum of the first 50 positive even integers is 2 + 4 + 6 + 8 + … + 100. As with the example is Lesson 2, these numbers can be regrouped into 25 pairs of numbers each of which has a sum of 2 + 100 = 102. Therefore, their sum is 25(102) = 2,550.
14. 14 Let n = Nora”s age now, and m = Mary”s age now. If 3 years ago, Nora was half as old
as Mary is now:
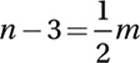
If Mary is 4 years older than Nora:
m = 4 + n
Subtract 4:
m − 4 = n
Substitute n = m − 4:
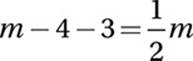
Simplify:
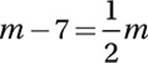
Multiply by 2:
2m − 14 = m
Subtract m and add 14:
m = 14
15. 4,200 Let x = the total number of seats in the stadium.
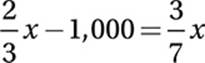
Subtract ![]() x:
x:
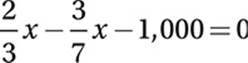
Add 1,000:
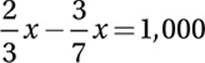
Combine like terms:
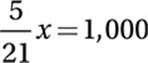
Multiply by ![]() :
:
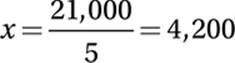
16. 0.20 Let g = the cost, in dollars, of one gumdrop, and c = the cost, in dollars, of one candy bar.
4c + 2g = 2.80
3c + 2g = 2.20
Subtract:
c = 0.60
Substitute c = 0.60:
4(0.60) + 2g = 2.80
Simplify:
2.40 + 2g = 2.80
Subtract 2.40:
2g = 0.40
Divide by 2:
g = 0.20
17. 6
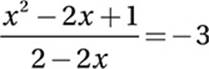
Factor:
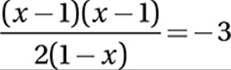
Multiply by −1:
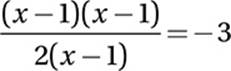
Simplify:
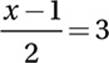
Multiply by 2:
x − 1 = 6
18. 12 We can just choose a number to work with, like 10. If we subtract 3 from this number then multiply the result by 4, we get 4(10 − 3) = 28. If we multiply it by 4 and then subtract a mystery number, we get 4(10) − x = 40 − x.
28 = 40 − x
Subtract 40:
−12 = −x
Multiply by −1:
12 = x
19. A If 5 green chips are worth m dollars, then each green chip is worth m/5 dollars. If a red chip is worth 2 dollars more than a green chip, then each red chip is worth m/5 + 2 dollars. If each blue chip is worth 2 dollars more than a red chip, then each blue chip is worth m/5 + 4 dollars. Therefore, 10 blue chips and 5 red chips are worth 10(m/5 + 4) + 5(m/5 + 2) = 2m + 40 + m + 10 = 3m + 50 dollars.
20. B The average speed is equal to the total distance divided by the total time. The total distance is 200 miles. The time for the first hundred miles is (100 miles/50 mph) = 2 hours, and the time for the second hundred miles is (100 miles/75 mph) = 4/3 hours. Therefore the total time of the trip is 2 + 4/3 = 10/3 hours, and the average speed is
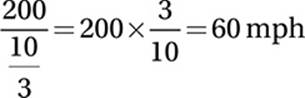
21. D
3m(m2 × 2m)
Parentheses:
3m(2m3)
Multiply:
6m4
22. C Assume the cost of living in 1980 was $100. If this increased by 20% from 1980 to 1990, then the cost of living in 1990 was 1.20($100) = $120. If the increase from 1980 to 2000 was 50%, then the cost of living in 2000 was 1.50($100) = $150. The percent increase from 1990 to 2000 is therefore