Cracking the GRE Premium (2015)
Part III How to Crack the Math Section
9 The Geography of the Math Section
10 Numbers and Equations
11 Real World Math
12 Geometry
13 Math Et Cetera
Chapter 9 The Geography of the Math Section
This chapter contains an overview of the content and structure you’ll see on the Math sections of the GRE. It provides valuable information on pacing strategies and the various question formats you’ll encounter on the GRE. It also goes over how to use basic test-taking techniques such as Process of Elimination and Ballparking as they relate to math questions. After finishing this chapter, you’ll have a good idea of what the Math section of the GRE looks like and some basic approaches to help you navigate it.
WHAT’S IN THE MATH SECTION
The GRE Math section primarily tests math concepts you learned in seventh through tenth grades, including arithmetic, algebra, and geometry. ETS alleges that the Math sections test the reasoning skills that you’ll use in graduate school, but what the Math section primarily tests is your comfort level with some basic math topics and your ability to take a test with strange-looking questions under timed conditions.
Junior High School?
The Math section of the GRE mostly tests how much you remember from the math courses you took in seventh, eighth, ninth, and tenth grades. But here’s some good news: GRE math is easier than SAT math. Why? Because many people study little or no math in college. If the GRE tested college-level math, everyone but math majors would bomb the test.
If you’re willing to do a little work, this is good news for you. By brushing up on the modest amount of math you need to know for the test, you can significantly increase your GRE Math score. All you have to do is shake off the dust.
The Math section of the exam consists of two 35-minute sections, each of which will consist of 20 questions. The first 7 or 8 questions of each section will be quantitative comparisons (quant comp, for short). The remainder will consist of multiple-choice or numeric-entry questions.
Predictable Triggers
The beauty of a standardized test is that it is, well, standardized. Standardized means predictable. We know exactly what ETS is going to test and how they’re going to test it. The math side of the test consists of a series of utterly predictable triggers, to which we have designed a series of highly scripted responses. ETS wants you to see each problem as a new challenge to solve. What you will find, however, is that there are only about 20 math concepts that are being tested. All of the questions you will see are just different ways of asking about these different concepts. Most of these concepts you already know. Once you recognize what’s being tested, even the trickiest questions become familiar and easy to solve.
It’s Really a Reading Test
In constructing the Math section, ETS is limited to the math that nearly everyone has studied: arithmetic, basic algebra, basic geometry, and elementary statistics. There’s no calculus (or even precalculus), no trigonometry, and no major-league algebra or geometry. Because of these limitations, ETS has to resort to traps in order to create hard problems. Even the most commonly missed GRE math problems are typically based on relatively simple principles. What makes the problems difficult is that these simple principles are disguised.

Head to your Premium
Portal to watch topnotch
Princeton Review
instructors talk about the
GRE Math section and
walk you through sample
problems.
Many test takers have no problem doing the actual calculations involved in the math questions on the GRE; in fact, you’ll even be allowed to use a calculator (more on that soon). However, on this test your ability to carefully read the problems and figure out how to set them up is more important than your ability to make calculations.
As you work through this section, don’t worry about how quickly you’re doing the problems. Instead, take the time to really understand what the questions are asking; pay close attention to the wording of the problems. Most math errors are the result of careless mistakes caused by not reading the problem carefully enough!
Read and Copy Carefully
You can do all the calculations right and still get a question wrong. How? What if you solve for x but the question asked for the value of x + 4? Ugh. Always reread the question before you choose an answer. Take your time and don’t be careless. The problem will stay on the screen as long as you want it to, so reread the question and double-check your work before answering it.
Or how about this? The radius of the circle is 5, but when you copied the picture onto your scratch paper, you accidentally made it 6. Ugh! If you make a mistake copying down information from the screen, you’ll get the question wrong no matter how perfect your calculations are. You have to be extra careful when copying down information.
THE CALCULATOR
As we mentioned before, on the GRE you’ll be given an on-screen calculator. The calculator program on the GRE is a rudimentary one that gives you the five basic operations: addition, subtraction, multiplication, division, and square root, plus a decimal function and a positive/negative feature. It also follows the order of operations, or PEMDAS (more on this topic in Chapter 10). The calculator also has the ability to transfer the answer you’ve calculated directly into the answer box for certain questions. The on-screen calculator can be a huge advantage—if it’s used correctly!
As you might have realized by this point, ETS is not exactly looking out for your best interests. Giving you a calculator might seem like an altruistic act, but rest assured that ETS knows that there are certain ways in which calculator use can be exploited. Keep in mind the following:

1. Calculators Can’t Think. Calculators are good for one thing and one thing only: calculation. You still have to figure out how to set up the problem correctly. If you’re not sure what to calculate, then a calculator isn’t helpful. For example, if you do a percent calculation on your calculator and then hit “Transfer Display,” you will have to remember to move the decimal point accordingly, depending on whether the question asks for a percent or a decimal.

2. The Calculator as a Liability. ETS will give you questions that you can solve with a calculator, but the calculator can actually be a liability. You will be tempted to use it. For example, students who are uncomfortable adding, subtracting, multiplying, or dividing fractions may be tempted to convert all fractions to decimals using the calculator. Don’t do it. You are better off mastering fractions than avoiding them. Working with exponents and square roots is another way in which the calculator will be tempting but may yield really big and awkward numbers or long decimals. You are much better off learning the rules of manipulating exponents and square roots. Most of these problems will be faster and cleaner to solve with rules than with a calculator. The questions may also use numbers that are too big for the calculator. Time spent trying to get an answer out of a calculator for problems involving really big numbers will be time wasted. Find another way around.

3. A Calculator Won’t Make You Faster. Having a calculator should make you more accurate, but not necessarily faster. You still need to take time to read each problem carefully and set it up. Don’t expect to blast through problems just because you have a calculator.

4. The Calculator Is No Excuse for Not Using Scratch Paper. Scratch paper is where good technique happens. Working problems by hand on scratch paper will help to avoid careless errors or skipped steps. Just because you can do multiple functions in a row on your calculator does not mean that you should be solving problems on your calculator. Use the calculator to do simple calculations that would otherwise take you time to solve. Make sure you are still writing steps out on your scratch paper, labeling results, and using set-ups. Accuracy is more important than speed!
Of course, you should not fear the calculator; by all means, use it and be grateful for it. Having a calculator should help you eliminate all those careless math mistakes.
GEOGRAPHY OF A MATH SECTION
Math sections contain 20 questions each. Test takers are allowed 35 minutes per section. The first 7 or 8 questions of each math section are quantitative comparisons, while the remainder are a mixed bag of problem solving, all that apply, numeric entry, and charts and graphs. Each section covers a mixture of algebra, arithmetic, quantitative reasoning, geometry, and real-world math.
QUESTION FORMATS
Much like the Verbal section, the Math section on the GRE contains a variety of different question formats. Let’s go through each question format and discuss how to crack it.
Standard Multiple Choice
These questions are the basic five-answer multiple-choice questions. These are great candidates for POE (Process of Elimination) strategies we will discuss later in this chapter.
Multiple Choice, Multiple Answer
These questions appear similar to the standard multiple-choice questions; however, on these you will have the opportunity to pick more than one answer. There can be anywhere from three to eight answer choices. Here’s an example of what these will look like:
If 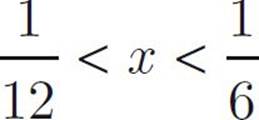 , then which of the following could be the value of x ?
, then which of the following could be the value of x ?
Indicate all such values.
![]()
![]()
![]()
![]()
![]()
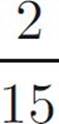
![]()
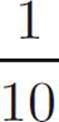
![]()
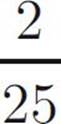
Your approach on these questions won’t be radically different from the approach you use on standard multiple-choice questions. But obviously, you’ll have to consider all of the answers—make sure you read each question carefully and remember that more than one answer can be correct. For example, for this question, you’d click on choices (C) and (D). You must select every correct choice to get credit for the problem.
Quantitative Comparison Questions
Quantitative comparison questions, hereafter affectionately known as “quant comp” questions, ask you to compare Quantity A to Quantity B. These questions have four answer choices instead of five, and all quant comp answer choices are the same. Here they are:
![]() Quantity A is greater.
Quantity A is greater.
![]() Quantity B is greater.
Quantity B is greater.
![]() The two quantities are equal.
The two quantities are equal.
![]() The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
Your job is to compare the two quantities and choose one of these answers.
Quant comp problems test the same basic arithmetic, algebra, and geometry concepts as do the other GRE math problems. So, to solve these problems, you’ll apply the same techniques you use on the other GRE math questions. But quant comps also have a few special rules you need to remember.
There Is No “E”
Because there are only four choices on quant comp questions, after you use POE to eliminate all of the answer choices you can, your odds of guessing correctly are even better. Think about it this way: Eliminating even one answer on a quant comp question will give you a one-in-three chance of guessing correctly.
If a Quant Comp Question Contains Only Numbers, the Answer Can’t Be (D)
Any quant comp problem that contains only numbers and no variables must have a single solution. Therefore, on these problems, you can eliminate choice (D) immediately because the larger quantity can be determined. For example, if you’re asked to compare ![]() and
and ![]() , you can determine which fraction is larger, so the answer cannot be (D).
, you can determine which fraction is larger, so the answer cannot be (D).
Compare, Don’t Calculate
You don’t always have to calculate the exact value of each quantity before you compare them. After all, your mission is simply to compare the two quantities. It’s often helpful to treat the two quantities as though they were two sides of an equation. Anything you can do to both sides of an equation, you can also do to both quantities. You can add the same number to both sides, you can multiply both sides by the same positive number, and you can simplify a single side by multiplying it by one.
Do only as much work
as you need to.
If you can simplify the terms of a quant comp, you should always do so.
Here’s a quick example:
![]()

![]() Quantity A is greater.
Quantity A is greater.
![]() Quantity B is greater.
Quantity B is greater.
![]() The two quantities are equal.
The two quantities are equal.
![]() The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
Here’s How to Crack It
Don’t do any calculating! Remember: Do only as much work as you need to in order to answer the question! The first thing you should do is eliminate (D). After all, there are only numbers here. After that, get rid of numbers that are common to both columns (think of this as simplifying). Both columns contain a 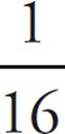 and a
and a ![]() , so because we’re talking about addition, they can’t make a difference to the outcome. With them gone, you’re merely comparing the
, so because we’re talking about addition, they can’t make a difference to the outcome. With them gone, you’re merely comparing the ![]() in column A to the
in column A to the ![]() in column B. Now we can eliminate (C) as well—after all, there is no way that
in column B. Now we can eliminate (C) as well—after all, there is no way that ![]() is equal to
is equal to ![]() . So, we’re down to two choices, (A) and (B). If you don’t remember how to compare fractions, don’t worry—it’s covered in Chapter 11 (Real World Math). The answer to this question is (B).
. So, we’re down to two choices, (A) and (B). If you don’t remember how to compare fractions, don’t worry—it’s covered in Chapter 11 (Real World Math). The answer to this question is (B).
![]()
Okay, let’s talk about another wacky question type you’ll see in the Math section.
Numeric Entry
Some questions on the GRE won’t even have answer choices, and you’ll have to generate your own answer. Here’s an example:
![]()
Each month, Renaldo earns a commission of 10.5% of his total sales for the month, plus a salary of $2,500. If Renaldo earns $3,025 in a certain month, what were his total sales?

Click on the answer box and type in a number.
Backspace to erase.
Here’s How to Crack It
On this type of question, POE is not going to help you! That means if you’re not sure how to do one of these questions, you should immediately move on. Leave it blank and come back to it in your second pass through the test.
If Renaldo earned $3025, then his earnings from the commission on his sales are $3025 − $2500 = $525. So, $525 is 10.5% of his sales. Set up an equation to find the total sales: 525 = 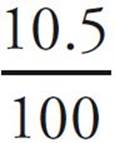 x where x is the amount of the sales. Solving this equation, x = 5000. (We’ll review how to set up and solve equations like this in later chapters.)
x where x is the amount of the sales. Solving this equation, x = 5000. (We’ll review how to set up and solve equations like this in later chapters.)
To answer this question, you’d enter 5,000 into the box. Alternately, you could transfer your work directly from the on-screen calculator to the text box.
![]()
MAXIMIZE YOUR SCORE
As you’re probably aware by now, doing well on the Math section will involve more than just knowing some math. It will also require the use of some good strategies. Let’s go through some good strategies now. Make sure you read this section carefully; it will be important for you to keep these techniques in mind as you work through the content chapters that follow this one!
The Two Roles of Techniques
The techniques are there to ensure that the questions that you should get right, you do get right. A couple of careless errors on easy questions will kill your score. The techniques are not just tools; they are proven standard approaches that save time and effort and guarantee points. Use these techniques on every question. Turn them into habits that you use every time.
Take the Easy Test First
The new GRE offers the opportunity to mark a question and return to it. Since all questions count equally toward your score, why not do the easy ones first? Getting questions right is far more important than getting to every question, so start with the low hanging fruit. There is no law that says you have to take the test in the order in which it is given. If you see a question you don’t like, keep moving. Play to your strengths and get all of the questions that you’re good at in the bank, before you start spending time on the hard ones. It makes no sense to spend valuable minutes wrestling with hard questions while there are still easy ones on the table. It makes even less sense if you end up having to rush some easy ones (making mistakes in the process), as a result. Free yourself from numerical hegemony! Take the easy test first!
Bend, Don’t Push
Eighty percent of the errors on the math side of the test are really reading errors. It is a four-hour test and at some point during these four hours your brain is going to get tired. When this happens you will read, see, or understand questions incorrectly. Once you see a problem wrong, it is nearly impossible to see it correctly. When this happens, even simple problems can become extremely frustrating. If you solve a problem and your answer is not one of the choices, this is what has happened. When you would swear that a problem can’t be solved, this is what has happened. When you have absolutely no idea how to solve a problem, this is what has happened. If you find yourself with half a page full of calculations and are no closer to the answer, this is what has happened. You are in La La Land. Once you are in La La Land, you can continue to push on that problem all day and you won’t get any closer.
There is a good chance that you are already familiar with this frustration. The first step is to learn to recognize it when it is happening. Here are some keys to recognizing when you are off track.
You know you are in La La Land when…
· You have spent more than three minutes on a single problem.
· Your hand is not moving.
· You don’t know what to do next.
· Your answer is not one of the choices.
· You’re spending lots of time with the calculator and working with some ugly numbers.
Once you recognize that you are in La La Land, get out. Continuing to push on a problem, at this point, is a waste of your time. You could easily spend three or four precious minutes on this problem and be no closer to the answer. Spend those three or four minutes on other questions. That time should be yielding you points, not frustration.
After you have done two or three other questions, return to the one that was giving you trouble. Most likely, the reason it was giving you trouble is that you missed something or misread something the first time around. If the problem is still difficult, walk away again.

This is called Bend, Don’t Push. The minute you encounter any resistance on the test, walk away. Bend. There are plenty of other easier points for you to get with that time. Then return to the problem a few questions later. It’s okay to take two or three runs at a tough problem. If you run out of time before returning to the question, so be it. Your time is better spent on easier problems anyway, since all problems count the same.
Forcing yourself to walk away can be difficult, especially when you have already invested time in a question. You will have to train yourself to recognize resistance when it occurs, to walk away, and then to remember to come back. Employ this technique anytime you are practicing for the GRE. It will take some time to master. Be patient and give it a chance to work. With this technique, there are no questions that are out of your reach on the GRE.
POE: Ballparking and Trap Answers
Use Process of Elimination whenever you can on questions that are in standard multiple-choice format. Always read the answer choices before you start to solve a math problem because often they will help guide you—you might even be able to eliminate a couple of answer choices before you begin to calculate the answer.
Two effective POE tools are Ballparking and Trap Answers.
You Know More Than You Think
Say you were asked to find 30 percent of 50. Wait—don’t do any math yet. Let’s say that you glance at the answer choices and you see these:
![]() 5
5
![]() 15
15
![]() 30
30
![]() 80
80
![]() 150
150
Think about it. Whatever 30 percent of 50 is, it must be less than 50, right? So any answer choice that’s greater than 50 can’t be right. That means you should eliminate both (D) and (E) before you even do any calculations! Thirty percent is less than half, so we can get rid of anything greater than 25, which means that choice (C) is gone too. What is 10% of 50? Eliminate choice (A). You’re done. The only answer left is (B). This process is known as Ballparking. Remember that the answers are part of the question. There are more than four times the number of wrong answers on the GRE as there are right ones. If it were easy to find the right ones, you wouldn’t need this book. It is almost always easier to identify and eliminate the wrong answers than it is to calculate the right one. Just make sure that you are using your scratch paper to eliminate answer choices instead of keeping track in your head.
Ballparking helps you eliminate answer choices and increases your odds of zeroing in on the correct answer. The key is to eliminate any answer choice that is “out of the ballpark.”
Let’s look at another problem:
![]()
A 100-foot rope is cut so that the shorter piece is ![]() the length of the longer piece. What is the length of the shorter piece in feet?
the length of the longer piece. What is the length of the shorter piece in feet?
![]() 75
75
![]() 66
66![]()
![]() 50
50
![]() 40
40
![]() 33
33![]()

Need More Math
Review?
Check out Math Workout
for the GRE for even more
math review.
Here’s How to Crack It
Now, before we dive into the calculations, let’s use a little common sense. The rope is 100 feet long. If we cut the rope in half, each part would be 50 feet. However, we didn’t cut the rope in half; we cut it so that there’s a longer part and a shorter part. What has to be true of the shorter piece then? It has to be less than 50 feet. If it weren’t, it wouldn’t be shorter than the other piece. So looking at our answers, we can eliminate (A), (B), and (C) without doing any real math. That’s Ballparking. By the way, the answer is (D).
![]()
Trap Answers
ETS likes to include “trap answers” in the answer choices to their math problems. Trap answers are answer choices that appear correct upon first glance. Often these answers will look so tempting that you’ll choose them without actually bothering to complete the necessary calculations. Watch out for this! If a problem seems way too easy, be careful and double-check your work.
Look at the this problem:
![]()
The price of a jacket is reduced by 10%. During a special sale, the price is discounted by another 10%. The special sale price is what percent less than the original price of the jacket?
![]() 15%
15%
![]() 19%
19%
![]() 20%
20%
![]() 21%
21%
![]() 25%
25%
Here’s How to Crack It
The answer might seem like it should be 20 percent. But wait a minute: Does it seem likely that the GRE is going to give you a problem that you can solve just by adding 10 + 10? Probably not. Choice (C) is a trap answer.
To solve this problem, imagine that the original price of the jacket is $100. After a 10 percent discount the new price is $90. But now when we take another 10 percent discount, we’re taking it from $90, not $100. 10 percent of 90 is 9, so we take off another $9 from the price and our final price is $81. That represents a 19 percent total discount because we started with a $100 jacket. The correct answer is (B).
![]()
HOW TO STUDY
Make sure you learn the content of each of the following chapters before you go on to the next one. Don’t try to cram everything in all at once. It’s much better to do a small amount of studying each day over a longer period; you will master both the math concepts and the techniques if you focus on the material a little bit at a time. Just as we have been telling you in earlier chapters, let the content sink in by taking short study breaks between study sessions and giving yourself plenty of time to prepare for the GRE. Slow and steady wins the race!
Practice, Practice, Practice
Practice may not make perfect, but it sure will help. Use everyday math calculations as practice opportunities. Balance your checkbook without a calculator! Make sure your check has been added correctly at a restaurant, and figure out the exact percentage you want to leave for a tip. The more you practice simple adding, subtracting, multiplying, and dividing on a day-to-day basis, the more your arithmetic skills will improve for the GRE.

Your Premium Portal contains
tons of informational
videos, practice tests,
helpful articles, and more
to help with your GRE
preparation. Head over
there and take advantage
of this fantastic resource!
After you work through this book, be sure to practice doing questions on our online tests and on real GREs. There are always sample questions at www.gre.org, and practice will rapidly sharpen your test-taking skills.
Finally, unless you trust our techniques, you may be reluctant to use them fully and automatically on the real GRE. The best way to develop that trust is to practice before you get to the real test.
Summary
· The GRE contains two 35-minute Math sections. Each section has 20 questions.
· The GRE tests math concepts up to about the tenth-grade level of difficulty.
· You will be allowed to use a calculator on the GRE. The calculator is part of the on-screen display.
· The Math section employs a number of different question formats, including multiple choice, numeric entry, and quantitative comparison questions.
· Use the Two-Pass system on the Math section. Find the easier questions and do them first. Use your remaining time to work some of the more difficult questions.
· When you get stuck on a problem, walk away. Do a few other problems to distract your brain, and then return to the question that was giving you problems.
· Ballpark or estimate the answers to math questions and eliminate answers that don’t make sense.
· Watch out for trap answers. If an answer seems too easy or obvious, it’s probably a trap.
· Always do your work on your scratch paper, not in your head. Even when you are Ballparking, make sure that you are eliminating answer choices on your scratch paper. If your hand isn’t moving, you’re stuck and you need to walk away, or you’re doing work in your head, which leads to errors.