Barron's GRE, 18th Edition (2009)
Part 4. QUANTITATIVE ABILITY: TACTICS, STRATEGIES, PRACTICE, AND REVIEW
Chapter 12. Quantitative Comparison Questions
One half of the 28 questions on the quantitative section of the GRE are quantitative comparisons. Unless you took the SAT before 2005, it is very likely that you have never seen questions of this type and certainly never learned the correct strategies for answering them. Don’t worry. In this chapter you will learn all of the necessary tactics. If you master them, you will quickly realize that quantitative comparisons are the easiest mathematics questions on the GRE and will wish that there were more than 14 of them.
Before the first quantitative comparison question appears on the screen, you will see these instructions.
Directions: This question consists of two quantities, one in Column A and one in Column B. You are to compare the two quantities and decide whether
the quantity in Column A is greater;
the quantity in Column B is greater;
the two quantities are equal;
the relationship cannot be determined from the information given.
Common information: Information concerning one or both of the quantities to be compared is centered above the two columns. A symbol that appears in both columns represents the same thing in Column A as it does in Column B.
Before learning the different strategies for solving this type of question, let’s clarify these instructions. In quantitative comparison questions there are two quantities, one in Column A and one in Column B, and it is your job to compare them.
|
You should click on |
if |
|
The quantity in Column A is greater. The quantity in Column B is greater. The two quantities are equal. The relationship cannot be determined from the information given. |
The quantity in Column A is greater all the time, no matter what. The quantity in Column B is greater all the time, no matter what. The two quantities are equal all the time, no matter what. The answer is not one of the first three choices. |
This means, for example, that if you can find a single instance when the quantity in Column A is greater than the quantity in Column B, then you can immediately eliminate two choices: the answer cannot be “The quantity in Column B is greater,” and the answer cannot be “The two quantities are equal.” In order for the answer to be “The quantity in Column B is greater,” the quantity in Column B would have to be greater all the time; but you know of one instance when it isn’t. Similarly, since the quantities are not equal all the time, the answer can’t be “The two quantities are equal.” The correct answer, therefore, is either “The quantity in Column A is greater” or “The relationship cannot be determined from the information given.” If it turns out that the quantity in Column A is greater all the time, then that is the answer; if, however, you can find a single instance where the quantity in Column A is not greater, the answer is “The relationship cannot be determined from the information given.”
By applying the tactics that you will learn in this chapter, you will probably be able to determine which of the choices is correct; if, however, after eliminating two of the choices, you still cannot determine which answer is correct, quickly guess between the two remaining choices and move on.
Before learning the most important tactics for handling quantitative comparison questions, let’s look at two examples to illustrate the preceding instructions.
EXAMPLE 1
|
Column A |
Column B |
|
|
1 < x < 3 |
||
|
x2 |
2x |
|
· ![]() The quantity in Column A is greater.
The quantity in Column A is greater.
· ![]() The quantity in Column B is greater.
The quantity in Column B is greater.
· ![]() The two quantities are equal.
The two quantities are equal.
· ![]() The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
SOLUTION. In each column, x represents the same thing — a number between 1 and 3. If x is 2, then x2 and 2x are each 4, and in this case the two quantities are equal. We can, therefore, eliminate the first two choices: neither Column A nor Column B is greater all the time. However, in order for the correct answer to be “The two quantities are equal,” the columns would have to be equal all the time. Are they? Note that although 2 is the only integerbetween 1 and 3, it is not the only number between 2 and 3: x could be 1.1 or 2.5 or any of infinitely many other numbers. And in those cases the quantities are not equal (For example, 2.52 = 6.25, whereas 2(2.5) = 5). The columns are not always equal, and so the correct answer is the fourth choice: “The relationship cannot be determined from the information given.”
HELPFUL HINT
Right now, memorize the instructions for answering quantitative comparison questions. When you take the GRE, dismiss the instructions for these questions immediately — do not spend even one second reading the directions (or looking at the sample problems).
EXAMPLE 2
|
Column A |
Column B |
|
|
p and q are primes |
||
|
p + q = 12 |
||
|
p |
8 |
|
· ![]() The quantity in Column A is greater.
The quantity in Column A is greater.
· ![]() The quantity in Column B is greater.
The quantity in Column B is greater.
· ![]() The two quantities are equal.
The two quantities are equal.
· ![]() The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
SOLUTION. Since 5 and 7 are the only primes whose sum is 12, p could be 5 or 7. In either case, p is less than 8, and so the quantity in Column B is greater, all the time. Note that although 1 + 11 = 12, p cannot be 11, because 1 is not a prime [See Section 14-A].
NOTE: To simplify the discussion, throughout the rest of this chapter, in the explanations of the answers to all sample questions and the Model Tests, the four answer choices will be referred to as A, B, C, and D, respectively. For example, we will write
The correct answer is B.
rather than
The correct answer is “The quantity in Column B is greater.”
Testing Tactics
![]() Replace Variables with Numbers
Replace Variables with Numbers
Many problems that are hard to analyze because they contain variables become easy to solve when the variables are replaced by simple numbers.
TACTIC 1 is the most important tactic in this chapter. Using it properly will earn you more points on the quantitative comparison questions of the GRE than you can gain by applying any of the others. Be sure to master it!
Most quantitative comparison questions contain variables. When those variables are replaced by simple numbers such as 0 or 1, the quantities in the two columns become much easier to compare.
The reason that TACTIC 1 is so important is that it guarantees that on any quantitative comparison question that involves variables, you will be able to immediately eliminate two of the four choices, and very often a third choice as well, leaving you with at least a 50% chance of guessing correctly, and often a certainty. Try the following example, and then read the explanation very carefully.
EXAMPLE 3
|
Column A |
Column B |
|
|
a < b < c < d |
||
|
ab |
cd |
SOLUTION.
· Replace a, b, c, and d with easy-to-use numbers which satisfy the condition a < b < c < d: for example, a = 1, b = 3, c = 6, d = 10. [See the guidelines that follow to learn why 1, 2, 3, 4 is not the best choice.]
· Evaluate the two columns: ab = (1)(3) = 3, and cd = (6)(10) = 60.
· So in this case, the quantity in Column B is greater.
· Does that mean that B is the correct answer? Not necessarily. The quantity in Column B is greater this time, but will it be greater every single time, no matter what?
· What it does mean is that neither A nor C could possibly be the correct answer: Column A can’t be greater every single time, no matter what because it isn’t greater this time; and the quantities aren’t equal every single time, no matter what because they aren’t equal this time.
So in the few seconds that it took you to plug in 1, 3, 6, and 10 for a, b, c, and d, you were able to eliminate two of the four choices. You now know that the correct answer is either B or D, and if you could do nothing else, you would now guess with a 50% chance of being correct.
But, of course, you will do something else. You will try some other numbers. But which numbers? Since the first numbers you chose were positive, try some negative numbers this time.
· Let a = –5, b = –3, c = –2, and d = –1.
· Evaluate: ab = (–5)(–3) = 15 and cd = (–2)(–1) = 2.
· So in this case, the quantity in Column A is greater.
· Column B is not greater all the time. B is not the correct answer.
· The correct answer is D: The relationship cannot be determined from the information given.
NOTES:
1. If for your second substitution you had chosen 3, 7, 8, 10 or 2, 10, 20, 35 or any four positive numbers, Column B would have been bigger. No matter how many substitutions you made, Column B would have been bigger each time, and you would have incorrectly concluded that B was the answer. In fact, if the given condition had been 0 < a < b < c < d, then B would have been the correct answer.
2. Therefore, knowing which numbers to plug in when you are using TACTIC 1 is critical. As long as you comply with the conditions written above the columns, you have complete freedom in choosing the numbers. Some choices, however, are much better than others.
Here are some guidelines for deciding which numbers to use when applying TACTIC 1.
|
1. |
The very best numbers to use first are: 1, 0, and −1. |
|
2. |
Often, fractions between 0 and 1 are useful. |
|
3. |
Occasionally, “large” numbers such as 10 or 100 can be used. |
|
4. |
If there is more than one letter, it is permissible to replace each with the same number. |
|
5. |
Do not impose any conditions not specifically stated. In particular, do not assume that variables must be integers. For example, 3 is not the only number that satisfies 2 < x < 4 (2.1, 3.95, and π all work). The expression a < b< c < d does not mean that a, b, c, d are integers, let alone consecutive integers (which is why we didn’t choose 1, 2, 3, and 4 in Example 3), nor does it mean that any or all of them are positive. |
When you replace the variables in a quantitative comparison question with numbers, remember:
|
If the value in Column A |
eliminate B and C — |
|
is ever greater: |
the answer must be A or D. |
|
If the value in Column B |
eliminate A and C — |
|
is ever greater: |
the answer must be B or D. |
|
If the two columns are |
eliminate A and B — |
|
ever equal: |
the answer must be C or D. |
You have learned that, no matter how hard a quantitative comparison is, as soon as you replace the variables, two choices can immediately be eliminated; and if you can’t decide between the other two, just guess. This guarantees that in addition to correctly answering all the questions that you know how to solve, you will be able to answer correctly at least half, and probably many more, of the questions that you don’t know how to do.
Practice applying TACTIC 1 on these examples.
EXAMPLE 4
|
Column A |
Column B |
|
|
m > 0 and m ≠ 1 |
||
|
m2 |
m3 |
EXAMPLE 5
|
13y |
15y |
EXAMPLE 6
|
w + 11 |
w – 11 |
EXAMPLE 7
|
The perimeter of a rectangle whose area is 18 |
The perimeter of a rectangle whose area is 28 |
EXAMPLE 8
|
|
|
|
3a |
4c |
SOLUTION 4. Use TACTIC 1. Replace m with numbers satisfying m > 0 and m≠ 1.

The answer is D.
SOLUTION 5. Use TACTIC 1. There are no restrictions on y, so use the best numbers: 1, 0, –1.

The answer is D.
SOLUTION 6. Use TACTIC 1. There are no restrictions on w, so use the best numbers: 1, 0, –1.

Guess A. We let w be a positive number, a negative number, and 0. Each time, Column A was greater. That’s not proof, but it justifies an educated guess. [The answer is A. Clearly, 11 > −11 and if we add w to each side, we get: w + 11 > w − 11.]
SOLUTION 7. What’s this question doing here? How can we use TACTIC 1? Where are the variables that we’re supposed to replace? Well, in each column there are rectangles, and the variables are their lengths and widths.
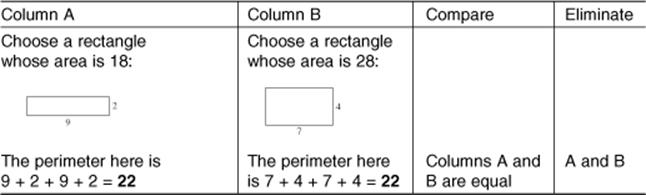
Keep Column B, but take a different rectangle of area 18 in Column A:

The answer is D.
SOLUTION 8. Use TACTIC 1. First, try the easiest number: let t = 0. Then a, b, and c are each 0, and in this case, the columns are equal — they’re both 0. Eliminate A and B. Now, try another number for t. The obvious choice is 1, but then a, b, and c will all be fractions. To avoid this, let t = 6. Then, ![]() , and
, and ![]() . This time,
. This time, ![]() and
and ![]() and 4b = 4(3) = 12. Again, the two columns are equal. Choose C.
and 4b = 4(3) = 12. Again, the two columns are equal. Choose C.
NOTE: You should consider answering this question directly (i.e., without plugging in numbers), only if you are very comfortable with both fractions and elementary algebra. Here’s the solution:
![]()
Therefore, 2c = t, and 4c = 2t. Since ![]() . So, 4c = 3a. The answer is C.
. So, 4c = 3a. The answer is C.
![]() Choose an Appropriate Number
Choose an Appropriate Number
This is just like TACTIC 1. We are replacing a variable with a number, but the variable isn’t mentioned in the problem.
EXAMPLE 9
|
Column A |
Column B |
|
Every band member is either 15, 16, or 17 years old. |
|
|
One third of the band members are 16, and |
|
|
twice as many band members are 16 as 15. |
|
|
The number of 17-year-old band members |
The total number of 15- and 16-year-old band members |
If the first sentence of Example 9 had been “There are n students in the school band, all of whom are 15, 16, or 17 years old,” the problem would have been identical to this one. Using TACTIC 1, you could have replaced n with an easy-to-use number, such as 6, and solved: ![]() are 16 years old; 1 is 15, and the remaining 3 are 17. The answer is C.
are 16 years old; 1 is 15, and the remaining 3 are 17. The answer is C.
The point of TACTIC 2 is that you can plug in numbers even if there are no variables. As discussed in TACTIC 3, Chapter 12, this is especially useful on problems involving percents, in which case 100 is a good number, and problems involving fractions, in which case the LCD of the fractions is a good choice. However, the use of TACTIC 2 is not limited to these situations. Try using TACTIC 2 on the following three problems.
EXAMPLE 10
|
Column A |
Column B |
|
The perimeter of a square and the |
|
|
circumference of a circle are equal. |
|
|
The area of the circle |
The area of the square |
EXAMPLE 11
|
Jen, Ken, and Len divided a cash prize. |
|
|
Jen took 50% of the money and spent |
|
|
Ken took 40% of the money and spent |
|
|
The amount that Jen spent |
The amount that Ken spent |
EXAMPLE 12
|
Column A |
Column B |
|
Eliane types twice as fast as Delphine. |
|
|
Delphine charges 50% more per page than Eliane. |
|
|
Amount Eliane earns in 9 hours |
Amount Delphine earns in 12 hours |
SOLUTION 10. First use TACTIC 1, Chapter 10: draw a diagram.
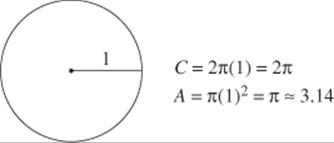
Then use TACTIC 2: choose an easy-to-use number. Let the radius of the circle be 1. Then its area is π. Let s be the side of the square:
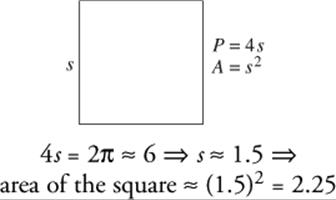
The answer is A.
SOLUTION 11. Use TACTIC 2. Assume the prize was $100. Then Jen took $50 and spent ![]() . Ken took $40 and spent
. Ken took $40 and spent ![]() . The answer is C.
. The answer is C.
SOLUTION 12. Use TACTIC 2. Choose appropriate numbers. Assume Delphine can type 1 page per hour and Eliane can type 2. Assume Eliane charges $1.00 per page and Delphine charges $1.50. Then in 9 hours, Eliane types 18 pages, earning $18.00. In 12 hours, Delphine types 12 pages, earning 12 × $1.50 = $18.00. The answer is C.
![]() Make the Problem Easier: Do the Same Thing to Each Column
Make the Problem Easier: Do the Same Thing to Each Column
A quantitative comparison question can be treated as an equation or an inequality. Either:

In solving an equation or an inequality, you can always add the same quantity to each side or subtract the same quantity from each side. Similarly, in solving a quantitative comparison, you can always add the same quantity to each column or subtract the same quantity from each column. You can also multiply or divide each side of an equation or inequality by the same quantity, but in the case of inequalities you can do this only if the quantity is positive. Since you don’t know whether the columns are equal or unequal, you cannot multiply or divide by a variable unless you know that it is positive. If the quantities in each column are positive you may square them or take their square roots.
To illustrate the proper use of TACTIC 3, we will give alternate solutions to three of the examples which we already solved using TACTIC 1.
EXAMPLE 4
|
Column A |
Column B |
|
|
m > 0 and m ≠ 1 |
||
|
m2 |
m3 |
|
EXAMPLE 5
|
13y |
15y |
EXAMPLE 6
|
w + 11 |
w − 11 |
|
|
Column A |
Column B |
|
|
SOLUTION 4. Divide each column by m2 (that’s OK — m2 is positive): |
|
|
This is a much easier comparison. Which is greater, m or 1? We don’t know. We know m > 0 and m ≠ 1, but it could be greater than 1 or less than 1. The answer is D.
|
SOLUTION 5. Subtract13y from each column: |
13y − 13y = 0 |
15y − 13y = 2y |
Since there are no restrictions on y, 2y could be greater than, less than, or equal to 0. The answer is D.
|
SOLUTION 6. Subtract w from each column: |
|
|
|
11 |
−11 |
Clearly, 11 is greater than −11. Column A is greater.
Here are five more examples on which to practice TACTIC 3.
EXAMPLE 13
|
Column A |
Column B |
|
|
|
EXAMPLE 14
|
(43 + 59)(17 − 6) |
(43 + 59)(17 + 6) |
EXAMPLE 15
|
(43 − 59)(43 − 49) |
(43 – 59)(43 + 49) |
EXAMPLE 16
|
Column A |
Column B |
|
|
a is a negative number |
||
|
a2 |
–a2 |
|
EXAMPLE 17
|
|
|
|
|
Column A |
Column B |
|
|
SOLUTION 13. |
||
|
Subtract |
|
|
|
Since |
SOLUTION 14.
|
Divide each column by (43 + 59): |
|
|
Clearly, (17 + 6) > (17 − 6). The answer is B.
SOLUTION 15. CAUTION: (43 − 59) is negative, and you may not divide the columns by a negative number.
The easiest alternative: Column A, being the product of 2 negative numbers, is positive, whereas Column B is negative. Column A is greater.
|
Column A |
Column B |
|
|
SOLUTION 16. |
||
|
Add a2 to each column: |
a2 + a2 = 2a2 |
−a2 + a2 = 0 |
Since a is negative, 2a2 is positive. The answer is A.
|
SOLUTION 17. |
||
|
Square each column: |
|
|
The answer is C.
![]() Ask “Could They Be Equal?” and “Must They Be Equal?”
Ask “Could They Be Equal?” and “Must They Be Equal?”
TACTIC 4 has many applications, but is most useful when one of the columns contains a variable and the other contains a number. In this situation ask yourself, “Could they be equal?” If the answer is “yes,” eliminate A and B, and then ask, “Must they be equal?” If the second answer is “yes,” then C is correct; if the second answer is “no,” then choose D. When the answer to “Could they be equal?” is “no,” we usually know right away what the correct answer is. In both questions, “Could they be equal” and “Must they be equal,” the word they refers, of course, to the quantities in Columns A and B.
Let’s look at a few examples.
EXAMPLE 18
|
Column A |
Column B |
|
The sides of a triangle are 3, 4, and x |
|
|
x |
5 |
EXAMPLE 19
|
56 < 5c < 64 |
|
|
c |
12 |
EXAMPLE 20
|
School A has 100 teachers and School B has 200 teachers. |
|
|
Each school has more female teachers than male teachers. |
|
|
The number of female teachers at School A |
The number of female teachers at School B |
EXAMPLE 21
|
Column A |
Column B |
|
(m + 1)(m + 2)(m + 3) = 720 |
|
|
m + 2 |
10 |
EXAMPLE 22
|
The perimeter of a rectangle whose area is 21 |
20 |
SOLUTION 18. Could they be equal? Could x = 5? Of course. That’s the all-important 3-4-5 right triangle. Eliminate A and B. Must they be equal? Must x = 5? If you’re not sure, try drawing an acute or an obtuse triangle. The answer is No. Actually, x can be any number satisfying: 1 < x < 7. (See KEY FACT J12, the triangle inequality, and the figure below.) The answer is D.
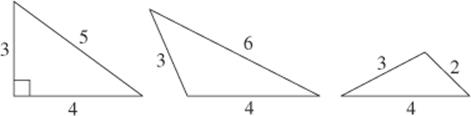
SOLUTION 19. Could they be equal? Could c = 12? If c = 12, then 5c = 60, so, yes, they could be equal. Eliminate A and B. Must they be equal? Must c = 12? Could c be more or less than 12? BE CAREFUL: 5 × 11 = 55, which is too small; and 5 × 13 = 65, which is too big. Therefore, the only integer that c could be is 12; but c doesn’t have to be an integer. The only restriction is that 56 < 5c < 64. If 5c were 58 or 61.6 or 63, then c would not be 12. The answer is D.
SOLUTION 20. Could they be equal? Could the number of female teachers be the same in both schools? No. More than half (i.e., more than 100) of School B’s 200 teachers are female, but School A has only 100 teachers in all. The answer is B.
SOLUTION 21. Could they be equal? Could m + 2 = 10? No, if m + 2 = 10, then m + 1 = 9 and m + 3 = 11, and 9 × 10 × 11 = 990, which is too big. The answer is not C, and since m + 2 clearly has to be smaller than 10, the answer is B.
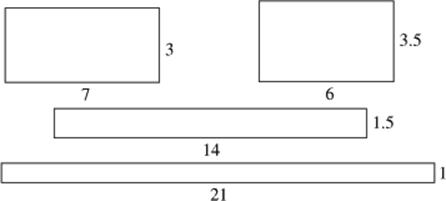
SOLUTION 22. Could they be equal? Could a rectangle whose area is 21 have a perimeter of 20? Yes, if its length is 7 and its width is 3: 7 + 3 + 7 + 3 = 20. Eliminate A and B. Must they be equal? If you’re sure that there is no other rectangle with an area of 21, then choose C; if you’re not sure, guess between C and D; if you know there are other rectangles of area 21, choose D.
There are other possibilities — lots of them; here are a 7 × 3 rectangle and a few other rectangles whose areas are 21:
![]() Don’t Calculate: Compare
Don’t Calculate: Compare
Avoid unnecessary calculations. You don’t have to determine the exact values of the quantities in Columns A and B; you just have to compare them.
TACTIC 5 is the special application of TACTIC 7, Chapter 10 (Don’t do more than you have to) to quantitative comparison questions. The proper use of TACTIC 5 allows you to solve many quantitative comparisons without doing tedious calculations, thereby saving you valuable test time that you can use on other questions. Before you start calculating, stop, look at the columns, and ask yourself, “Can I easily and quickly determine which quantity is greater without doing any arithmetic?” Consider Examples 23 and 24, which look very similar, but really aren’t.
EXAMPLE 23
|
Column A |
Column B |
|
37 × 3 43 |
30 × 53 |
EXAMPLE 24
|
37 × 43 |
39 × 47 |
Example 23 is very easy. Just multiply: 37 × 43 = 1591 and 30 × 53 = 1590. The answer is A.
Example 24 is even easier. Don’t multiply. In far less time than it takes to do the multiplications, you can see that 37 < 39 and 43 < 47, so clearly 37 × 43 < 39 × 47. The answer is B. You don’t get any extra credit for taking the time to determine the value of each product!
Remember: do not start calculating immediately. Always take a second or two to glance at each column. In Example 23 it’s not at all clear which product is larger, so you have to multiply. In Example 24, however, no calculations are necessary.
These are problems on which poor test-takers do a lot of arithmetic and good test-takers think! Practicing TACTIC 5 will help you become a good test-taker.
Now, test your understanding of TACTIC 5 by solving these problems.
EXAMPLE 25
|
Column A |
Column B |
|
The number of years from 1776 to 1929 |
The number of years from 1767 to 1992 |
EXAMPLE 26
|
452 + 252 |
(45 + 25)2 |
EXAMPLE 27
|
45(35 + 65) |
45 × 35 + 45 × 65 |
EXAMPLE 28
|
Marianne earned a 75 on each of her first three math tests and an 80 on her fourth and fifth tests. |
|
|
Marianne’s average after 4 tests |
Marianne’s average after 5 tests |
SOLUTIONS 25–28
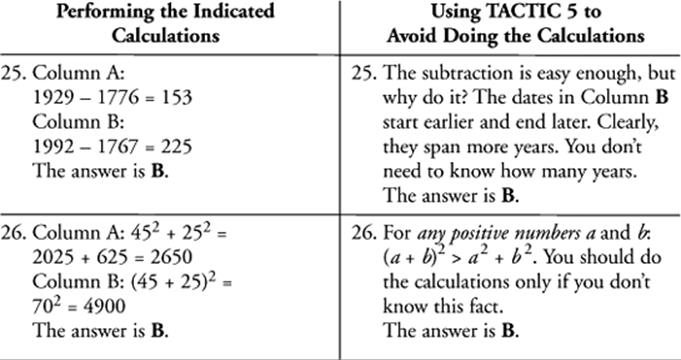
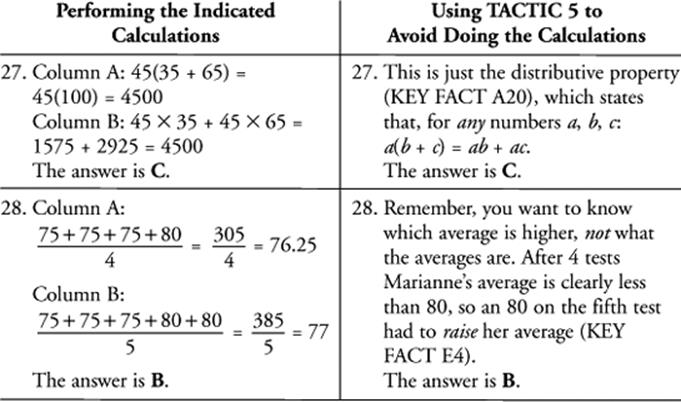
CAUTION: TACTIC 5 is important, but don’t spend a lot of time looking for ways to avoid a simple calculation.
![]() Know When to Avoid Choice D
Know When to Avoid Choice D
If the quantities in Columns A and B are both fixed numbers, the answer cannot be D.
Notice that D was not the correct answer to any of the six examples discussed under TACTIC 5. Those problems had no variables. The quantities in each column were all specific numbers. In each of the next four examples, the quantities in Columns A and B are also fixed numbers. In each case, either the two numbers are equal or one is greater than the other. It can always be determined, and so D cannot be the correct answer to any of these problems. If, while taking the GRE, you find a problem of this type that you can’t solve, just guess: A, B, or C. Now try these four examples.
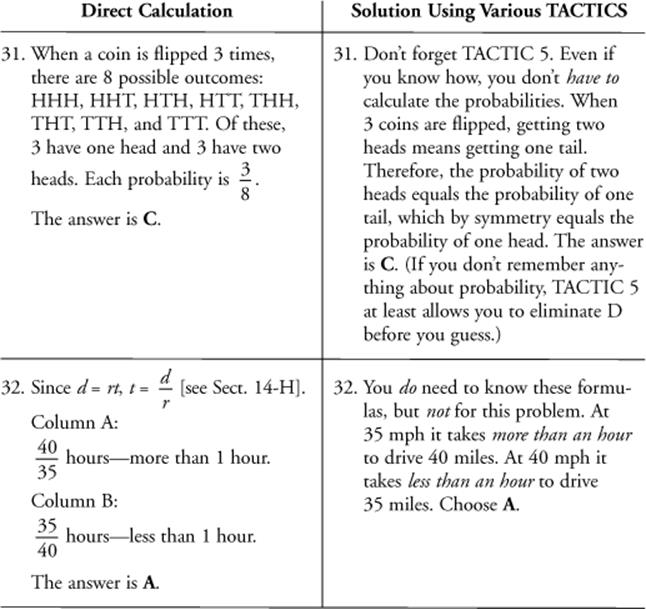
EXAMPLE 29
|
Column A |
Column B |
|
The number of seconds in one day |
The number of days in one century |
EXAMPLE 30
|
The area of a square whose sides are 4 |
Twice the area of an equilateral triangle whose sides are 4 |
EXAMPLE 31
|
Column A |
Column B |
|
|
Three fair coins are flipped. |
||
|
The probability of getting one head |
The probability of getting two heads |
|
EXAMPLE 32
|
The time it takes to drive 40 miles at 35 mph |
The time it takes to drive 35 miles at 40 mph |
Here’s the important point to remember: don’t choose D because you can’t determine which quantity is bigger; choose D only if nobody could determine it. You may or may not know how to compute the number of seconds in a day, the area of an equilateral triangle, or a certain probability, but these calculations can be made.
SOLUTIONS 29–32

Practice Exercises
Quantitative Comparison Questions
|
Column A |
Column B |
|
|
1. |
197 + 398 + 586 |
203 + 405 + 607 |
|
x > 0 |
||
|
2. |
10 x |
|
|
3. |
The time that it takes to type 7 pages at a rate of 6 pages per hour |
The time that it takes to type 6 pages at a rate of 7 pages per hour |
|
cd < 0 |
||
|
4. |
(c + d)2 |
c2 + d2 |
|
a, b, and c are the measures of the angles of isosceles triangle ABC. |
|||
|
x, y, and z are the measures of the angles of right triangle XYZ. |
|||
|
5. |
The average of a, b, and c |
The average of x, y, and z |
|
|
b < 0 |
||
|
6. |
6b |
b6 |
|
7. |
The area of a circle whose radius is 17 |
The area of a circle whose diameter is 35 |
|
Line k goes through (1,1) and (5,2). |
||
|
8. |
The slope of line k |
The slope of line m |
|
x is a positive integer |
||
|
9. |
The number of multiples of 6 between 100 and x + 100 |
The number of multiples of 9 between 100 and x + 100 |
|
Column A |
Column B |
|
|
x + y = 5 |
||
|
y − x = −5 |
||
|
10. |
y |
0 |
|
11. |
|
|
|
|
||
|
12. |
The area of the shaded region |
12 |
|
The number of square inches in the |
||
|
13. |
The length of an edge of the cube |
6 inches |
|
1 < x < 4 |
||
|
14. |
πx |
x2 |
|
|
||
|
15. |
The area of ΔABC |
3 |
ANSWER KEY
|
1. B |
4. B |
7. B |
10. C |
13. C |
|
2. D |
5. C |
8. A |
11. A |
14. D |
|
3. A |
6. B |
9. D |
12. B |
15. D |
Answer Explanations
The direct mathematical solution to a problem is almost always the preferable one, so it is given first. It is often followed by one or more alternate solutions, indicated by a double asterisk, based on the various tactics discussed in this chapter. Occasionally, a solution based on one of the tactics is much easier than the straightforward one. In that case, it is given first.
1. (B)This can easily be solved in less than a minute by adding, but in only 5 seconds by thinking! Use TACTIC 5: don’t calculate; compare. Each of the three numbers in Column B is greater than the corresponding number in Column A.
2. (D)Use TACTIC 1. When x = 1, the columns are equal; when x = 2, they aren’t.
**Use TACTIC 3
|
Column A |
Column B |
|
|
10x |
|
|
|
Multiply each |
||
|
column by x (this |
||
|
is OK since x > 0): |
10x2 |
10 |
|
Divide each |
||
|
column by 10: |
x2 |
1 |
3. This is a much easier comparison. x2 could equal 1, but doesn’t have to. The answer is Choice D.
4. (A) You can easily calculate each of the times — by dividing 7 by 6 in Column A, and 6 by 7 in Column B. However, it is easier to just observe that the time in Column A is more than one hour, whereas the time in Column B is less than one hour.
5. (B) Use TACTIC 3
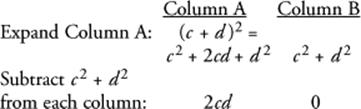
Since it is given that cd < 0, so is 2cd.
**If you can’t expand (c + d)2, use TACTIC 1. Replace c and d with numbers satisfying cd < 0.

Both times Column B was greater: choose B.
6. (C) The average of 3 numbers is their sum divided by 3. Since in any triangle the sum of the measures of the 3 angles is 180° [KEY FACT J1], the average in each column is equal to 180 ÷ 3 = 60.
**Use TACTIC 1. Pick values for the measures of the angles. For example, in isosceles ΔABC choose 70, 70, 40; in right ΔXYZ, choose 30, 60, 90. Each average is 60. Choose C.
7. (B) Since b < 0, 6b is negative, whereas b6 is positive.
**Use TACTIC 1. Replace b with numbers satisfying b < 0.

Both times Column B was greater: choose B.
8. (B) Again, use TACTIC 5: don’t calculate the two areas; compare them. The circle in Column A has a radius of 17, and so its diameter is 34. Since the circle in Column B has a larger diameter, its area is greater.
9. (A) Again, use TACTIC 5: don’t calculate either slope. Quickly, make a rough sketch of line k, going through (1,1) and (5,2), and draw line m perpendicular to it.
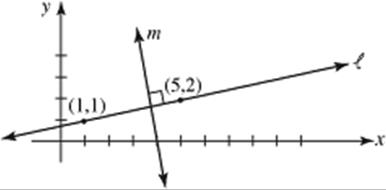
Line k has a positive slope (it slopes upward), whereas line m has a negative slope (it slopes downward). Column A is greater. [Note: the slope of k is ![]() and the slope of m is −4. See Section 14-N for all the facts you need to know about slopes.]
and the slope of m is −4. See Section 14-N for all the facts you need to know about slopes.]
**If you don’t know this fact about slopes, use TACTIC 6. The answer cannot be Choice D, and if two lines intersect, their slopes cannot be equal, so eliminate Choice C. Guess Choice A or B.
10. (D) Every sixth integer is a multiple of 6 and every ninth integer is a multiple of 9, so in a large interval there will be many more multiples of 6. But in a very small interval, there might be none or possibly just one of each.
**Use TACTIC 1. Let x = 1. Between 100 and 101 there are no multiples of 6 and no multiples of 9. Eliminate Choices A and B. Choose a large number for x: 100, for example. Between 100 and 200 there are many more multiples of 6 than there are multiples of 9. Eliminate Choice C.
11. 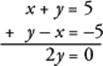
Since 2y = 0, y = 0.
**Use TACTIC 4. Could y = 0? In each equation, if y = 0, then x = –5. So, y can equal 0. Eliminate Choices A and B, and either guess between Choices C and D or try to continue. Must y = 0? Yes, when you have two linear equations in two variables, there is only one solution, so nothing else is possible.
12. (A) The arithmetic is annoying and time-consuming, but not difficult. However, you can avoid the arithmetic, if you know KEY FACT A24:
If 0 < x < 1 and n > 1, then xn < x.
Since ![]() , then
, then ![]() .
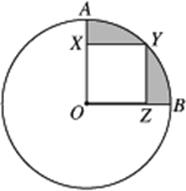
.
13. (B) The area of the shaded region is the area of quarter-circle AOB minus the area of the square. Since r = OA = 6, the area of the quarter-circle is ![]() . OY, the diagonal of the square, is 6 (since it is a radius of the circle), so OZ, the side of the square, is
. OY, the diagonal of the square, is 6 (since it is a radius of the circle), so OZ, the side of the square, is ![]() [KEY FACT J8]. So the area of the square is
[KEY FACT J8]. So the area of the square is ![]() . Finally, the area of the shaded region is 9π − 18, which is approximately 10.
. Finally, the area of the shaded region is 9π − 18, which is approximately 10.
**The solution above requires several steps. [See Sections 14-J, K, L to review any of the facts used.] If you can’t reason through this, you still should be able to answer this question correctly. Use TACTIC 6. The shaded region has a definite area, which is either 12, more than 12, or less than 12. Eliminate D. Also, the area of a curved region almost always involves π, so assume the area isn’t exactly 12. Eliminate Choice C. You can now guessbetween Choices A and B, but if you trust the diagram and know a little bit you can improve your guess. If you know that the area of the circle is 36π, so that the quarter-circle is 9π or about 28, you can estimate the shaded region. It’s well less than half of the quarter-circle, so less than 14 and probably less than 12. Guess Choice B.
14.(C) Use TACTIC 4. Could the edge be 6? Test it. If each edge is 6, the area of each face is 6 × 6 = 36, and since a cube has 6 faces, the total surface area is 6 × 36 = 216. The volume is 63 = 216. So the columns could be equal. Eliminate Choices A and B. If you have a sense that this is the only cube with this property, choose C. In fact, if you had no idea how to do this, you might use TACTIC 6, assume that there is only one way, eliminate Choice D, and then guess C. The direct solution is simple enough if you know the formulas. If e is the length of an edge of the cube, then the area is 6e2 and the volume is e3: 6e2 = e3 ⇒ 6 = e.
15. (D) There are several ways to do this. Use TACTIC 1: plug in a number for x. If x = 2, Column A is 2π, which is slightly more than 6, and Column B is 22 = 4. Column A is greater: eliminate Choices B and C. Must Column A be greater? If the only other number you try is x = 3, you’ll think so, because 32 = 9, but 3π > 9. But remember, x does not have to be an integer: 3.92 > 15, whereas 3.9π < 4π, which is a little over 12.
**Use TACTIC 4. Could πx = x2? Yes, if x = π. Must x = π? No.
**Use TACTIC 3. Divide each side by x: Now Column A is π and Column B is x. Which is bigger, π or x? We cannot tell.
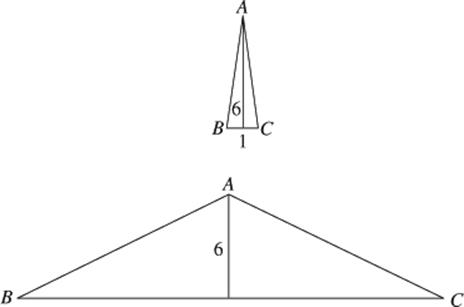
16. (D) Use TACTIC 4. Could the area of ΔABC = 3? Since the height is 6, the area would be 3 only if the base were 1: ![]() . Could BC = 1? Sure (see the figure). Must the base be 1? Of course not.
. Could BC = 1? Sure (see the figure). Must the base be 1? Of course not.