CHAPTER 3 LSAT Logic Games

In this chapter, you will learn:

 How to work each of the four types of games you might encounter on the Logic Games section

 How to diagram and symbolize the information presented to you in each game

 How to draw deductions from the information presented to you in each game

 The best techniques and methods for working each kind of question

 How to approach the Logic Games section as a whole

This chapter focuses on the Logic Games section (formally known as the Analytical Reasoning section). The cases in this chapter will teach you a six-step approach you can use to work every game you encounter. The Logic Games section can seem daunting at first, so we’ll break it down into parts. As noted in Chapter 1, the Logic Games section requires you to perform only two tasks: ordering and grouping. The test writers use some combination of those two tasks to create four different types of games.

This chapter introduces you to each of the four major game types that appear on the LSAT. You will learn the best way to:

  Determine what kind of game you’re working based on the information in the setup and the clues

  Diagram and symbolize the setup and the clues

  Make deductions from that information

  Answer each of the different kinds of questions you’ll come across

We’ll also discuss the best strategy for tackling the Logic Games section as a whole.

Accordingly, this chapter contains six cases. Four of them—Case 1, Case 3, Case 4, and Case 5—introduce a particular type of game. Those four cases include a sample game and a detailed explanation of how to work the sample game. Case 2 introduces you to conditional statements, which are a particularly important type of clue and can appear on any type of game. Finally, Case 6 discusses section-wide strategy.

Two important notes before you turn to the first case:

  As you’ll soon see firsthand, an effective Logic Games strategy involves a good bit of writing: you’ll draw a diagram, symbolize clues, and map out your answers to each question. Unfortunately, you’re not allowed to bring scratch paper into the LSAT. You have to do all your work in the blank space in your test booklet. As you practice, get in the habit of working in the small space you’ll have available to you.

  The sample games used in these cases are not representative of the average difficulty of the games you’ll see on test day. The games are teaching tools; they are designed to demonstrate the fundamentals of a sound approach to working games. Each case concludes with setup drills that reflect the difficulty of real games.

Practicing is the only way to truly get a sense of how hard logic games really are. The Logic Games sections in the practice tests included at the back of this book contain a mix of games that is representative of what you’re likely to encounter on the actual LSAT.

One-Tiered Ordering Games: Emily Walks the Dogs

This case serves two primary functions. First, it introduces the general approach you should use to work every logic game. That approach involves the following six steps:

1. Identify the game type

2. Begin your diagram

3. Symbolize the clues

4. Double-check your symbolizations

5. Make deductions

6. Answer the questions in the smartest order

Because you’ll use this same six-step approach on every game you encounter, this case is the longest case of this chapter. As you work different kinds of games and more difficult games, you’ll want to return to this case to review the fundamentals.

Second, this case introduces you to a particular type of logic game: one-tiered ordering games. One-tiered ordering games have been by far the most common type of game on recent LSATs. As noted in Chapter 1, the LSAC has released to the public 15 of the 20 LSATs that it administered between 2006 and 2010. Of the 60 games that appear on those LSATs, 24—or 40 percent—were one-tiered ordering games. That’s an average of just under two per test. Mastering one-tiered ordering games is therefore an indispensable component of success on test day.

We’ll introduce ordering games using a sample game, which we’ll walk through together step by step. If you want to take a shot at working it on your own beforehand, feel free. You might find the explanation of how to set up and work the game easier to understand if you’ve spent some time trying to work it yourself. But you don’t need to do so; after all, the purpose of this chapter is to introduce you to a new, more effective method of solving logic games.

A dog walker named Emily has been hired to walk six dogs: a Labrador, a Mutt, a Poodle, a Retriever, a Schnauzer, and a Terrier. She walks each dog exactly once, and she walks them one at a time. The order in which Emily walks the dogs must be consistent with the following:

She walks the Labrador some time before the Terrier.

She walks the Poodle immediately after the Mutt.

She walks the Retriever either immediately before or immediately after the Terrier.

She walks the Schnauzer fourth.

1. Which of the following could be the order, from first to last, in which Emily walks the dogs?

(A) L, T, R, S, M, P

(B) M, L, P, S, T, R

(C) T, R, L, S, M, P

(D) L, M, P, R, T, S

(E) R, L, T, S, M, P

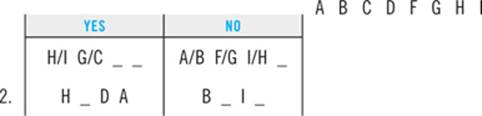
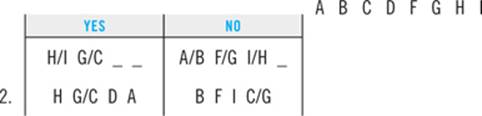
2. Which of the following must be false?

(A) Emily walks the Terrier second.

(B) Emily walks the Labrador third.

(C) Emily walks the Mutt third.

(D) Emily walks the Retriever sixth.

(E) Emily walks the Poodle sixth.

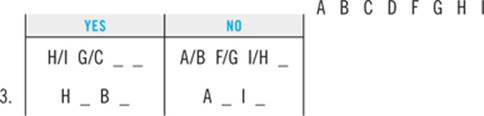
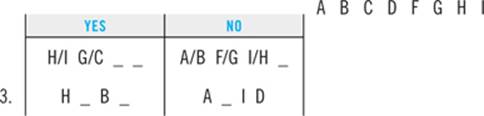
3. If Emily walks the Retriever third, which of the following must be true?

(A) Emily walks the Terrier fourth.

(B) Emily walks the Poodle sixth.

(C) Emily walks the Poodle fifth.

(D) Emily walks the Labrador second.

(E) Emily walks the Mutt first.

4. Which of the following must be false?

(A) Emily walks the Mutt first.

(B) Emily walks the Labrador second.

(C) Emily walks the Terrier fifth.

(D) Emily walks the Labrador first.

(E) Emily walks the Retriever third.

5. Which one of the following is a complete and accurate list of the positions in which Emily could walk the Retriever?

(A) 5, 6

(B) 3, 5

(C) 3, 5, 6

(D) 2, 3, 5, 6

(E) 1, 2, 3, 5, 6

6. If Emily walks the Mutt second, which of the following could be false?

(A) She walks the Labrador before she walks the Mutt.

(B) She walks the Terrier after she walks the Schnauzer.

(C) She walks the Retriever after she walks the Terrier.

(D) She walks the Schnauzer before she walks the Retriever.

(E) She walks the Poodle after she walks the Labrador.

STEP 1:  Identify the Game Type

To determine what kind of game you’re dealing with, look to language in the setup and language in the clues. It’s important that you read both the setup and the clues before you begin your diagram. Sometimes the information you need appears in the clues and sometimes there are clues in the setup.

Because you’re being asked to arrange the elements (the dogs) in sequential order (which one was walked first, second, etc., down to sixth), this is an ordering game. Because you’re assigning exactly one element to each slot in the game, this is a one-tiered ordering game (we’ll discuss a different kind of ordering game—two-tiered ordering games—in Case 4).

What’s the language in the setup that marks this as an ordering game? Here, the setup explicitly says “the order in which Emily walks the dogs.” The other language in this setup that is the hallmark of an ordering game is, “She walks each dog exactly once, and she walks them one at a time.” You’re putting things in order, one at a time. Here are some other examples of language the LSAT could use to set up an ordering game:

  Five basketball players are ranked by height from tallest to shortest. There are no ties.

  The new children’s book series has exactly eight chapters.

  A real-estate agent must show seven houses. She does not show any of the houses more than once, and no two houses are shown at the same time.

Similarly, comparative language in the clues is a strong indicator that this is an ordering game: Emily walks some dogs “before” and “after” other dogs. Clues that assign a particular element a numbered rank (“She walks the Schnauzer fourth”) are also an ordering-game staple. Here is some other language you might see in the clues of ordering games:

  Before and after

  Earlier and later

  Higher and lower

  More expensive and less expensive

  Taller and shorter

  Younger (or newer) and older

  Numbering language: “cannot be third,” “must be either first or last,” and so on

STEP 2:  Begin Your Diagram

Once you’ve classified the game as a one-tiered ordering game, you can begin drawing your diagram. Your goal is to draw a diagram that is a visually accurate representation of the logical relationship between the elements. In other words, when you’re trying to figure out what kind of diagram to draw, just ask yourself, “What does this game look like?”

This game asks you to create a list numbered 1 through 6 of the order in which Emily walks the dogs. So, your diagram will look like this:

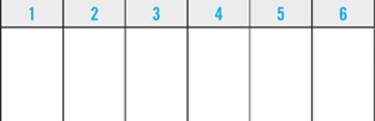
Next, you’ll symbolize the game’s elements and each of the clues. First, abbreviate each element using a letter. Then list the letters off to the side of the diagram so you can keep track of them as you work.

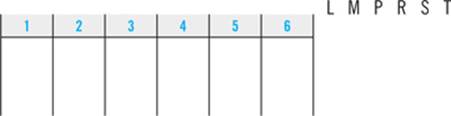
STEP 3:  Symbolize the Clues

Symbolize the clues in a vertical line off to the side of your diagram. Keep the space underneath your diagram clear because you’ll need to expand the diagram as you work the questions. The same principle that determined how you drew your diagram will now dictate how you symbolize each clue: What does it look like?

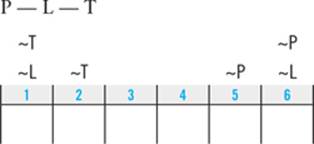
Clue 1: “She walks the Labrador some time before the Terrier.”

You don’t know exactly how far apart L and T have to be. It would be consistent with this clue for Emily to walk L first and T sixth, or she could walk L third and T fourth. All you know is that L will be somewhere to the left of T in the diagram. So you’ll symbolize this clue accordingly:

L — T

Then check off “L” and “T” on your list of elements. It’s important to get in the habit of doing this as you work. Once you’ve symbolized all the clues, if one of the elements is not checked off, you know it is a “free agent”; there are no restrictions on where it can go. This can be a powerful aid in working a game.

Clue 2: “She walks the Poodle immediately after the Mutt.”

Here, you know exactly how far apart these two elements have to be: wherever they are plugged into the diagram, M will immediately precede P. What will that look like?

MP

Clue 3: “She walks the Retriever either immediately before or immediately after the Terrier.”

Here again you know that wherever these two elements are plugged into the diagram, they’ll be right next to each other. While these two elements have to be adjacent, the order in which they must appear is not yet determined. In other words, your diagram could look like this:

RT

or it could look like this:

TR

and in either case the clue would be satisfied. Instead of using two separate boxes, you’ll use one and make a notation that indicates that the elements in the box can appear in either order.

R ↔ T

Clue 4: “She walks the Schnauzer fourth.”

The purpose of symbolizing clues is to help you figure out where to place the elements in your diagram. This clue skips straight to the punch line and places an element for you. Accordingly, you should symbolize this clue directly into your diagram:

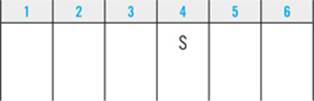
STEP 4:  Double-Check Your Symbolizations

The single most costly mistake you can make on the Logic Games section is to incorrectly symbolize a clue. You can easily wind up working through most of the questions before realizing your mistake. You can’t afford to lose that time. It is absolutely vital that you double-check your symbolizations before proceeding any further.

The most effective way to double-check your symbolizations is to translate them back into English. For example, you symbolized the first clue in this game like this:

L — T

Translated into English, that says, “Emily walks L before she walks T.” After making that translation, compare it to the language of the clue. Since your translation matches the language of the clue, you know you’ve symbolized that clue correctly. You’ll repeat this process for every clue before beginning to Make deductions.

It’s better to double-check this way than by re-symbolizing each clue. Why? If you misunderstood the clue the first time you read it, you’re likely to make the same mistake the second time and you’ll end up with the wrong symbolization again. Plus, when you translate your symbolization into English, the double-checking process is as simple as comparing your translation to the clue. If the two don’t match, you’ll spot it right away.

After double-checking your clues, you should have a diagram and clue list that looks like this:

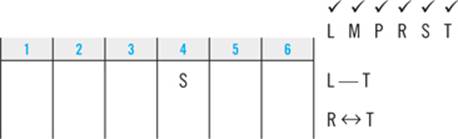
STEP 5:  Make Deductions

The final step before you begin working the questions is to investigate the clues to see if you can make any deductions about the placement of the elements in the game. It can be tempting to skip this step and dive straight into the questions—making deductions takes time, and time is of the essence. But these deductions will drastically reduce the time it takes you to answer the questions.

Many LSAT students initially find the process of making deductions to be a mysterious one. Fortunately, there are a few categories of deductions that show up repeatedly on the Logic Games section. And there is a consistent set of steps you can follow that will allow you to make those deductions.

Look for opportunities to make the following kinds of deductions:

1. Can’t-be-first-or-last deductions

2. Repeated-element deductions

3. Down-to-two deductions

4. Block-splitting deductions

The first deduction is relevant to those “before or after” clues. Think about it this way. If someone must stand in line after you, you can’t be the last in line. And if someone must come before you, you can’t be first.

For example, take the first clue in this game:

L — T

You can deduce from this clue that Emily cannot walk T first. If she did, it would be impossible for her to satisfy the condition that she walk L before she walks T. For similar reasons, you can deduce that she cannot walk L sixth.

The best way to symbolize that deduction is with a notation above your diagram:

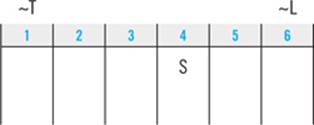
(Note: This book uses the “~” sign to mean “not.” Many test takers choose to represent “not” with a strike-through, so that “not T” would be symbolized “T.” Either method is fine; pick the one that you feel more comfortable with and use it consistently.)

The second clue (MP) is amenable to the same deduction: Emily cannot walk M last, and she cannot walk P first:

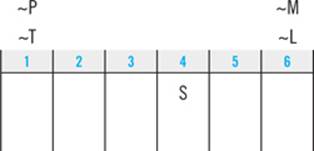
There is another, similar deduction you can make from this clue. M cannot be placed in any slot where it is impossible to place P in the slot immediately to the right. Since S must be fourth, you know that M cannot be third:

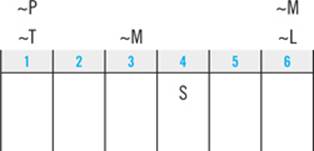
The third clue will not support this kind of deduction, as Emily can walk R and T in any order so long as she walks them consecutively.

Once you’ve completed the process of making can’t-be-first-or-last deductions, turn next to repeated-element deductions. Use a two-step process to make repeated-element deductions:

1. Identify any element that appears in more than one clue.

2. See if you can combine those clues to produce new information.

In this game, the only element that shows up in more than one clue is T, which appears in both the first (L — T) and third clues. And it’s possible to combine those clues to produce new information.

In plain English, the third clue tells you that R and T appear consecutively. As a consequence, it’s impossible for L to appear in between R and T. Since R and T are right next to each other and the first clue tells you that L must come before T, it follows that L also must come before R.

Symbolically,

L — T

plus

R ↔ T

equals

L — R ↔ T

This deduction functions as a new clue, which means you can make deductions based on it. This new clue will support two can’t-be-first-or-last deductions. Take a moment to see if you can make them.

First, you now know that L must come before R, so it follows that R can’t come first. Second, you now know that both R and T must come after L. So not only can L not be sixth, but it also can’t be fifth. It needs at least two available spaces after it to house both R and T. You can symbolize these new deductions directly into your diagram:

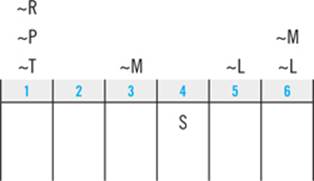
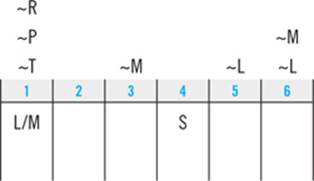
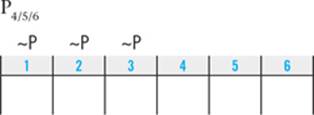
Next up, look for what we’ll call down-to-two deductions. In the Logic Games section, being able to limit a slot to only two elements is almost as valuable as being able to definitively place one element in that slot. While it’s rare to be able to definitively place an element, you’ll frequently be able to make a down-to-two deduction that limits a slot to two possibilities.

The question to ask is, “Is there any slot in this game that is so restricted that it can be occupied by only one of two elements?” Here, you know from your prior deductions that neither R nor P nor T can occupy the first slot. And since S must be fourth, you also know that S cannot occupy the first slot. Four of the six elements are thus barred from being first: only L and M remain. You can note that deduction directly into your diagram using a slash as an either/or symbol:

No other down-to-two deductions are available, so let’s turn to the final type of deduction, which is to look for possibilities of block-splitting. Block-splitting is one of the most commonly recurring concepts on the Logic Games section, showing up in all four types of games. The test writers frequently use it to generate correct and incorrect answers.

What is block-splitting? In this game, clues 2 and 3 require M and P and R and T to always appear right next to each other. Those clues create two-element “blocks.” The basic concept of block-splitting is that in a game that involves blocks of elements, you can’t place the nonblocked, single elements in a way that makes it impossible to place all of the blocks.

Here’s a simple example. Suppose Emily only had to walk three dogs—S, R, and T—but she still had to walk R and T consecutively. If Emily walked S second, there would be no way for her to legally walk all three dogs. Walking S second would split the R—T block.

Making a block-splitting deduction is the process of taking a moment at the beginning of the game to think about where you can place any multi-element blocks. Sometimes the need to preserve room to place the block will make it impossible to place a single, unblocked element in a particular slot in the game. To make a block-splitting deduction, follow these steps:

1. Identify all of the blocked elements.

2. Determine the various places within the game where the block(s) can be placed.

3. Look for any slots where placing a single, unblocked element would split the block (i.e., make it impossible to place the blocked elements anywhere).

In this game, you have two two-element blocks: MP and RT, and your diagram looks like this:

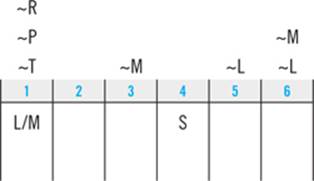
The blocks take up four slots, and there are only three slots to the left of S. So you know that one of the blocks must be in 5 and 6, and the other block must be somewhere in the first three slots.

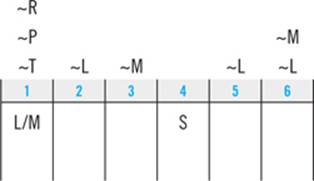
That enables you to make the following deduction: if you place one of the nonblocked elements in slot 2, you won’t have room to place both of the blocks. L is the only nonblocked element that you haven’t placed yet, so you can deduce that L can never go in slot 2:

If you found it difficult to follow the reasoning that led to that deduction, don’t worry. Block-splitting deductions are the most difficult kind of deduction to make. It also gets easier to make them the more you practice working games.

STEP 6:  Answer the Questions in the Smartest Order

The order in which the questions associated with a game appear is not the order in which you should work those questions. You want to work the questions in the way that is most helpful to you. That means you want to work easier questions before harder questions. You also want to work the questions in such a way that you can use the work you do on the first few questions to help you answer the last few questions. The most strategically advantageous order in which to work the questions is as follows:

1. Answer the Complete and Accurate List question.

2. Answer questions that give you more information to work with.

3. Answer the remaining questions.

Complete and Accurate List Questions.  The first question associated with your game about Emily walking the dogs is a Complete and Accurate List question. Complete and Accurate List questions ask, “Which of the following answer choices is an acceptable way to fill in every slot in this game?” These are by far the easiest kind of question you’ll see on the Logic Games section. If a game has one (and most games do), you should always work it first. How can you identify a Complete and Accurate List question? It will ask you to pick an arrangement that complies with all the clues, and it will always be the first question associated with the game.

1. Which of the following could be the order, from first to last, in which Emily walks the dogs?

(A) L, T, R, S, M, P

(B) M, L, P, S, T, R

(C) T, R, L, S, M, P

(D) L, M, P, R, T, S

(E) R, L, T, S, M, P

To answer a Complete and Accurate List question, take each clue and scan the answer choices looking for one that violates the rule that clue establishes.

Your first clue tells you that L must come before T. Scanning the answer choices, T is listed before L in answer choice C, so you can eliminate that choice. Answer B violates clue 2, answer E violates clue 3, and answer D violates clue 4, so the correct choice for question 1 is answer A.

Questions That Give You More Information.  Information is the coin of the realm in the Logic Games section. The more you know about where the elements must, can, or cannot go, the easier it is to work with the game. For that reason, questions that contain new information are generally easier and less time-consuming to work than questions that require you to work only with the information given in the setup.

In this game, questions 3 and 6 are examples of this kind of question: each of them instructs you to assume an additional fact that further limits the ways in which Emily can walk the dogs.

3. If Emily walks the Retriever third, which of the following must be true?

(A) Emily walks the Terrier fourth.

(B) Emily walks the Poodle sixth.

(C) Emily walks the Poodle fifth.

(D) Emily walks the Labrador second.

(E) Emily walks the Mutt first.

The first step in working this kind of question is to plug the new information directly into your diagram:

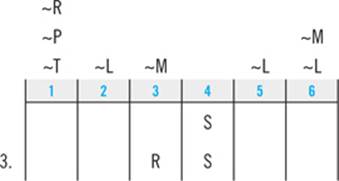
Next, you’ll combine that information with your clues and deductions. Start with any clue that applies to the same element(s) about which the question has given you new information. Here, the third clue tells you that T and R must appear consecutively. Since S must appear right after R, you know that T must appear right before R in slot 2:

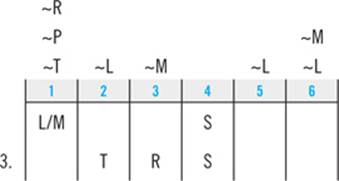
Since Emily must walk T second, you’ll immediately look down to the answer choices to see if that’s listed as one of the answer choices. As it turns out, it’s not, but if it had been, you could have selected it and moved on without doing any more work. Your goal on the Logic Games section is to do exactly as much work as you have to to get the right answer, and no more. Each time you place an element, check the answer choices to see if you’ve got the answer.

Your next step will be to combine the new information you have about T with any clues you have about T. From the first clue, you know that L must come before T. Since you know that T must be second, L must be first:

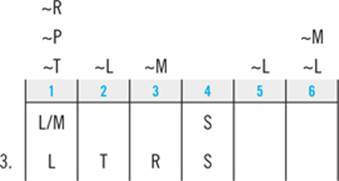
Once again, scan the answer choices to see if “L must be first” is among them. It’s not, so you’ll keep going. Only two slots remain open, and from the second clue you can determine that M and P must be fifth and sixth, respectively:

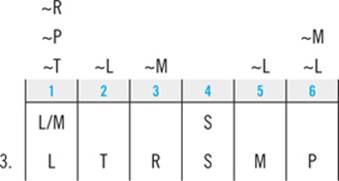
Just by virtue of knowing that R comes third, you’re able to completely fill in the game. As the diagram illustrates, the correct choice for question 3 is answer B: Emily must walk the Poodle sixth.

6. If Emily walks the Mutt second, which of the following could be false?

(A) She walks the Labrador before she walks the Mutt.

(B) She walks the Terrier after she walks the Schnauzer.

(C) She walks the Retriever after she walks the Terrier.

(D) She walks the Schnauzer before she walks the Retriever.

(E) She walks the Poodle after she walks the Labrador.

Pay close attention to language. What exactly is the question asking you to determine? Question 3 asks what must be true; question 6 asks what could be false. Another question may ask you what must be false or what could be true. It is crucial that you carefully note what the question is asking, and to keep it at the forefront of your mind as you work.

As it turns out, questions 3 and 6 are mirror images of each other: anything that must be true cannot be false. On a must-be-true question, you diagram the new information, definitively place as many other elements as possible, and pick an answer choice that matches what you’ve diagrammed. On a could-be-false question, the first two steps are the same, but instead of selecting the answer that matches your diagram, you eliminate it as an incorrect choice. It cannot be false (or in other words, it must be true).

Question 6 tells you that M comes second. First, you’ll plug that into the diagram:

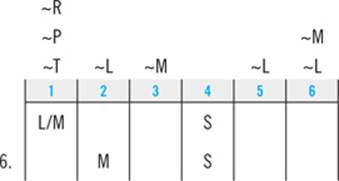
If M comes second, the second clue tells you P must come third:

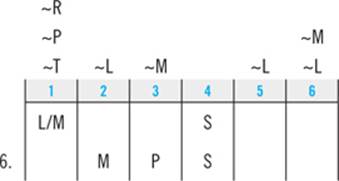
Scanning the answer choices reveals that you can’t cross anything out yet. Next, your down-to-two deduction tells you that if M is second, L must come first:

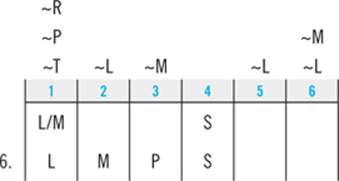
That tells you that L must come before both P and S, so you can eliminate answer choices A and E.

Finally, the third clue tells you that R and T must appear consecutively, so they go in slots 5 and 6. You don’t know what order R and T appear in, so you’ll place them using the “either/or” notation.

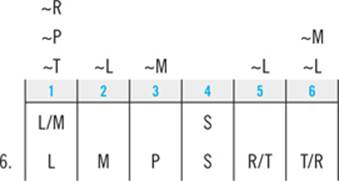
That tells you that S must come before both T and R, which eliminates answers B and D. That leaves you with answer C: “Emily walks the Retriever after she walks the Terrier.” Not necessarily! Emily could walk the Terrier after the Retriever, as your diagram clearly shows. Therefore, answer C could be false, so it is the right answer.

Again, carefully read the language of the question and always keep in mind what the question is asking you to determine. For question 6, if you thought you were looking for an answer that must be false instead of one that could be false, you would definitely waste a lot of time on a wild goose chase.

Questions That Do Not Give You New Information.  Having worked all of the questions that give you new information, you’ll finally turn to the questions that don’t. Use a three-step process to tackle such questions:

1. Can you answer this question using the clues and your deductions?

2. Can you answer this question using work you did on previous questions?

3. Can you answer this question using the process of elimination?

Each of the three remaining questions illustrates one step in that process.

2. Which of the following must be false?

(A) Emily walks the Terrier second.

(B) Emily walks the Labrador third.

(C) Emily walks the Mutt third.

(D) Emily walks the Retriever sixth.

(E) Emily walks the Poodle sixth.

Question 2 simply asks you to pick an answer choice that must be false based only on the information in the setup and the clues.

The correct answer to a question like this one is never merely a restatement of one of the clues. You might be able to use the clues to eliminate some incorrect answer choices, but arriving at the correct answer will always require you to make some kind of deduction.

The best place to start is with the deductions you already made. Here, that’s all it takes. You already deduced that M can never be in slot 3. That deduction makes answer C the correct choice.

4. Which of the following must be false?

(A) Emily walks the Mutt first.

(B) Emily walks the Labrador second.

(C) Emily walks the Terrier fifth.

(D) Emily walks the Labrador first.

(E) Emily walks the Retriever third.

Question 4 asks which of its answer choices must be false. On must-be-false questions, you can eliminate any answer choice that could be true.

Therefore, your first step is to check to see if any of the answer choices match up with any of your deductions to create a legal arrangement of the elements. Once again, you’re in luck. Your block-splitting deduction tells you that L can’t be second, so it must be false. Therefore, answer B is the correct choice.

But you noted above that block-splitting deductions are the most difficult kind of deduction to make. What would you do if you hadn’t made the block-splitting deduction? In that case, you would use the second tactic for approaching questions that don’t give you any new information: rely on the work you’ve done in answering previous questions.

If you hadn’t made the block-splitting deduction, at this point your diagram would look like this:

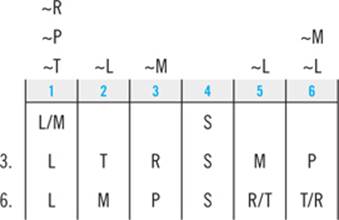
In the course of diagramming your answers to questions 3 and 6, you’ve already generated several examples of ways in which all six of the elements in the game could legally be placed. Accordingly, if your answers to those questions demonstrate that one or more of the answer choices to question 4 could be true, you can eliminate those choices. Using this tactic, you can eliminate answer choices D and E based on your answer to question 3 and answer choice C based on your answer to question 6.

All that’s left is to pick between answer A and answer B. Your work on previous questions does not enable you to eliminate either choice, so you’ll have to turn to your third and final tactic for these kinds of questions: using the process of elimination. There are only two choices left, so you can just pick one and diagram it. If it must be false, you’ve got your answer.

Start with answer choice A. Could it be true that Emily walks M first? If you plug M into slot 1, the second clue tells you that P must come second:

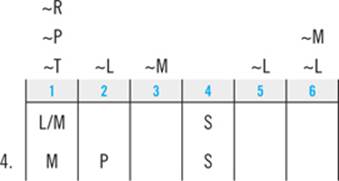
The third clue tells you that R and T must be in consecutive slots; the only place to make that happen is in slots 5 and 6:

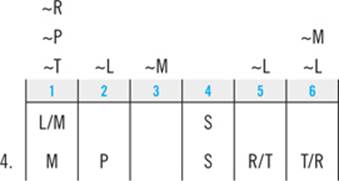
That forces L into slot 3:

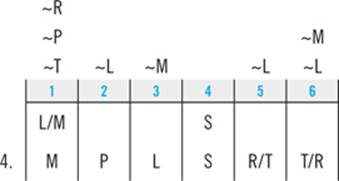
Having L in slot 3 and T in slot 5 or slot 6 satisfies the first clue, so this is a legal arrangement. Since it could be true that Emily walks M first, you can eliminate answer choice A, leaving answer B as the correct answer to question 4.

Your work on question 4 highlights two things. On the one hand, it is extremely helpful to take the time up front to Make deductions. On the other hand, if you overlook a deduction, it’s not the end of the world. You can still arrive at the correct answer to a question; it’s just going to take you longer.

Finally, turn to question 5.

5. Which one of the following is a complete and accurate list of the positions in which Emily could walk the Retriever?

(A) 5, 6

(B) 3, 5

(C) 3, 5, 6

(D) 2, 3, 5, 6

(E) 1, 2, 3, 5, 6

Don’t let the wording of the question confuse you; this is not the kind of question you should always work first. Not only is it not the first question associated with the game, but it asks you only about one element instead of every element in the game.

Here, you’re looking for a list of the slots where R could appear that is both accurate (no wrong answers included) and complete (no right answers excluded). The steps to working this question are the same. First you turn to your deductions. You know that R can’t go first, so you can eliminate choice E as inaccurate.

Next, you’ll use your work on previous questions:

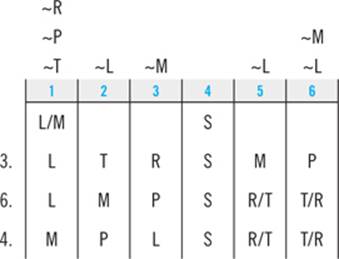
Your work on question 3 tells you that R can go third, so answer A is an incomplete list. Your work on questions 4 and 6 tells you that R can go sixth, so you can also eliminate answer B as incomplete.

The only choices left are answers C and D, and you can’t eliminate either one based on your answers to other questions, so you’ll have to use the process of elimination. Since the only difference between those two answers is whether R can go second, you’ll plug that into your diagram and see if you can make it work.

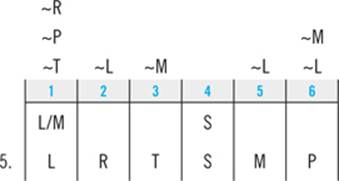
And you can: the third clue places T in slot 3; the second clue places M and P in 5 and 6; and the first clue places L in slot 1.

Since R can appear in slot 2, answer C is an incomplete list. Accordingly, choice D is the correct answer to question 5.

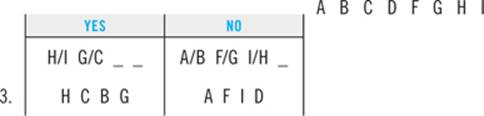
Clue Symbolization Drills

The game that you’ve just worked through is a relatively straightforward example of a one-tiered ordering game. There are many different ways the test writers can increase the difficulty level of one-tiered ordering games. By far the most common technique they use is giving you clues that are difficult to understand, difficult to symbolize, and difficult to work with. These symbolization drills are designed to introduce some of those more difficult clue types.

Instructions: Below are examples of clues applied to the setup of the sample game that might appear in one-tiered ordering games. Use the “what does it look like?” principle to symbolize each of these clues (remember you can input some clues directly into your diagram). Also make a note of any can’t-be-first-or-last deductions. Answers appear on the following page.

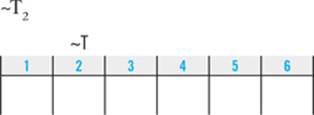
1. Emily cannot walk the Terrier second.

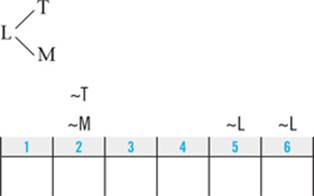
2. Emily must walk the Labrador before she walks both the Mutt and the Retriever.

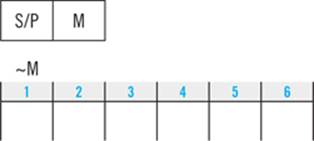
3. Emily must walk either the Schnauzer or the Poodle immediately before she walks the Mutt.

4. Emily must walk the Labrador before she walks the Terrier but after she walks the Poodle.

5. The Poodle must be one of the last three dogs Emily walks.

6. Emily must walk exactly two dogs in between the Mutt and the Retriever.

7. Emily must walk at least two dogs in between the Mutt and the Retriever.

8. Emily walks the Terrier either at some time before she walks the Labrador or at some time after she walks the Poodle, but not both.

9. Either Emily walks the Poodle before both the Retriever and the Mutt, or she walks both the Retriever and the Mutt before the Poodle.

10. Emily walks the Terrier before the Mutt, or else she walks the Terrier before the Labrador, but not both.

Clue Symbolization Answers

1. 

2. 

3. 

4. 

5. 

6. 

7. 

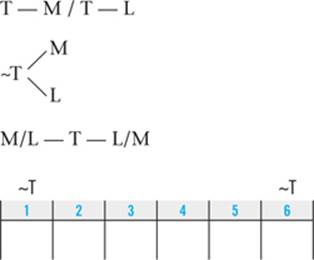
8. T — L/P — T
~(P — T — L)

Note that this clue does not support any can’t-be-first-or-last deductions.

9. 

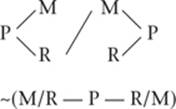
Note that this clue does not support any can’t-be-first-or-last deductions.

10. 

Working with Conditional Statements

As noted at the beginning of the chapter, there are only two tasks the Logic Games section will ask you to perform: ordering and grouping. Case 1 introduced you to ordering games. Before you can turn to grouping games, however, you need to take a moment to learn how to identify and work with a particular type of clue.

The purpose of this case is to introduce you to conditional statements. Working with conditional statements is essential to success on the Logic Games section. It is guaranteed that on test day you will have to symbolize and work with multiple clues that are conditional statements. In recent years, every single grouping game on the LSAT has had at least one conditional-statement clue. Many ordering games employ them as well.

This case will proceed in three parts. First, we’ll discuss what a conditional statement is, how to symbolize a basic conditional statement, and how to make the deduction that every conditional statement supports. Next, we’ll deal with translating and symbolizing more complex conditional statements. Last, you’ll have a chance to practice these skills with a series of drills.

Basic Conditional Statements

A conditional statement is an “if–then” statement. For example, “If something is an apple, then it is a fruit” is a conditional statement. We’ll call the portion of the statement that follows the “if” the condition, and the portion that follows the “then” we’ll label the consequence.

Each time you see a conditional statement on the Logic Games section, you’ll take the same three steps:

1. Abbreviate the elements that make up the statement.

2. Symbolize the statement using an arrow.

3. Symbolize the statement’s contrapositive.

For step 1, abbreviate “apple” as “A” and “fruit” as “F.”

Next, symbolize the conditional statement using an arrow. The condition—that’s the statement that follows “if”—goes in front of the arrow. The consequence—the statement that follows “then”—goes behind the arrow. So, “If something is an apple, then it is a fruit” becomes “A → F.”

Third, you’ll make the standard deduction that follows from every conditional statement. That deduction is known as the contrapositive. If something is an apple, then it must be a fruit. Therefore, if something is not a fruit, then it cannot be an apple. A conditional statement and its contrapositive are logically equivalent to one another: when you know a conditional statement is true, you can be certain that its contrapositive is also true.

Symbolically, to take the contrapositive of “A → F,” follow these two steps:

1. Flip sides. Take the element before the arrow and move it after the arrow. Take the element after the arrow and move it before the arrow.

2. Flip signs. Take any element that is positive and negate it. Take any element that is negative and make it positive.

Thus, the contrapositive of “A → F” is “~F → ~A.”

Working with Conditional Statements

You now know that two things are true:

A → F
~F → ~A

Based on those two conditional statements, what do you know if:

1. Something is an apple?

2. Something is not an apple?

3. Something is a fruit?

4. Something is not a fruit?

Again, start in plain English.

1. If something is an apple, then it must be a fruit.

2. If something is not an apple, does it follow that it is not a fruit? No. The thing could be an orange or a pear.

3. If you know that something is a fruit, does it follow that it must be an apple? No. Again, it could be another type of fruit.

4. If something is not a fruit, you can be sure that it is not an apple.

Conditional statements are based on their conditions. The statement only tells you something if the condition is satisfied. If the condition is not satisfied, the statement tells you nothing.

Understanding this distinction is critical to success on the Logic Games section. The first half of a conditional statement can be false, and the second half can still be true. Here’s an easy way to remember this rule: Follow the arrow.

A → F
~F → ~A

If you know A, the arrow points you to F. If you know ~F, the arrow points you to ~A. But if you know F or ~A, the conditional statement tells you nothing; you’re on the wrong side of the arrow. As long as you never go against the arrow, you won’t misinterpret a conditional statement.

Complex Conditional Statements: Multiple Elements

Statements in the form of “If A, then B” are the simplest kind of conditional statement. But the Logic Games section also employs conditional statements in more complicated forms. Fortunately, you can use a standard set of steps to symbolize these more complicated conditionals and accurately state their contrapositives.

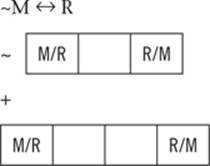
As an example, start with the statement, “If not A or B, then C and not D.” You can symbolize that statement using your standard “~” as a negative and the “&” and “/” signs for “and” and “or,” respectively:

~A / B → C & ~D

The tricky part is correctly writing out that statement’s contrapositive. To do so, follow these three steps:

1. Flip sides. This is the same as before: take the elements before the arrow and move them after the arrow, and vice versa.

2. Flip signs. This is also the same as before. Flip all negatives into positives, and negate anything that is positive.

3. Flip connectors. “And” becomes “or,” and “or” becomes “and.” Take any “&” and make it a “/.” Take any “/” and make it an “&.”

Here’s what those steps look like when applied to a conditional statement in the form of ~A / B → C & ~D:

1. C D → A B

2. ~C D → A ~B

3. ~C / D → A & ~B

That’s all there is to it. “If not C or D, then A and not B” is the contrapositive of the statement “If not A or B, then C and not D.”

Complex Conditional Statements: Ordering Clues

One type of complex conditional statement is particularly relevant. To illustrate it, return to the game you worked in Case 1. Suppose that game had included the following clue: “If Emily walks the Retriever before she walks the Terrier, then she must walk the Mutt before she walks the Schnauzer.”

You would symbolize such a clue like this:

R — T → M — S

Clues like this—conditional statements that dictate the order in which certain elements appear—have been very common on recent LSATs. To take its contrapositive, all you have to do is flip sides and flip signs:

1. M — S → R — T

2. ~(M — S) → ~(R — T)

In the context of the sample game, there’s a more useful way to flip signs. Recall that Emily must walk the dogs one at a time. If M is not before S, that means that M is after S. Thus, when you’re flipping signs on a clue like this, “before” becomes “after,” and “after” becomes “before.” That rule will allow you to diagram the contrapositive the same way you would diagram the other clues:

S — M → T — R

Complex Conditional Statements: Translating Phrases Other Than If–Then

The final skill you’ll need to work effectively with conditional statements is the ability to translate and symbolize conditional statements that use nonstandard language. For example, each of the following is a conditional statement:

1. B only if A

2. Not B unless A

3. All A are B

4. No A are B

5. B if, but only if, A

The following list offers ways each of these statements can be symbolized using the standard → sign for conditionals.

B only if A = B → A

Symbolizing “only if” statements can be tricky. In a standard “if–then” statement, whatever comes after “if” is placed in front of the arrow. By contrast, when the clue uses “only if” language, whatever comes after the “only if” is placed behind the arrow.

“Not B unless A” = B → A

Translating an “unless” statement into a conditional involves two steps:

1. Take what follows “unless” and make it the back half of your symbolization.

2. Take what comes before the “unless,” negate it, and make it the front half of your symbolization.

“All A are B” = A → B
“No A are B” = A → ~B

These two are fairly straightforward. The trick is recognizing that all-or-nothing statements like these are actually conditional statements.

“B if, but only if, A” = A → B and B → A

This is probably the trickiest type of conditional statement you might run across on test day. The reason it’s tricky is that it’s actually two conditional statements—(1) “B if A”; and (2) “B only if A”—disguised as one. That’s why it takes two separate symbolizations to diagram it correctly.

Conditional Statement Drills

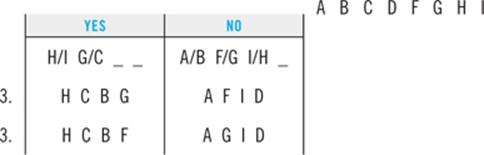
You’ll practice working with conditional statements in grouping games in the next case. Below are examples of conditional-statement clues that might appear in one-tiered ordering games. The clues refer back to the game you worked in Case 1 in which Emily walked the dogs. For each of these questions, symbolize the clue and symbolize the contrapositive. Answers follow.

1. Emily must walk the Mutt fifth if she does not walk the Terrier second.

2. Emily walks the Schnauzer second if, but only if, she walks the Retriever sixth.

3. If Emily walks the Mutt before the Poodle, then she walks the Terrier after the Labrador.

4. Emily walks the Retriever first, unless she walks the Schnauzer fifth.

5. Emily does not walk the Retriever first unless she walks the Schnauzer fifth.

6. If Emily walks the Mutt third, then she walks the Retriever immediately before she walks the Schnauzer.

7. If Emily walks the Terrier third, then she walks the Terrier before both the Labrador and the Schnauzer.

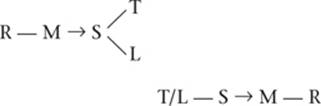
8. If Emily walks the Retriever before she walks the Mutt, then she walks the Schnauzer before both the Terrier and the Labrador.

1. ~T₂ → M₅

~M₅ → T₂

2. Emily walks the Schnauzer second if she walks the Retriever sixth.

R₆ → S₂

~S₂ → ~R₆

Emily walks the Schnauzer second only if she walks the Retriever sixth.

S₂ → R₆
~R₆ → ~S₂

3. M — P → L — T

T — L → P — M

4. ~R₁ → S₅

~S₅ → R₁

5. R₁ → S₅

~S₅ → ~R₁

6. 

7. 

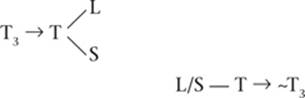
8. 

Grouping Games: Ralph Hosts a Dinner Party

The purpose of this case is to introduce grouping games. Of the 60 games that appeared on the 15 publicly available LSATs from 2006 to 2010, 16—about 27 percent—were grouping games. That means that, on average, one of the four games in a Logic Games section is a grouping game.

Recall from Case 1 the six-step method that you learned for tackling one-tiered ordering games:

1. Identify the game type

2. Begin your diagram

3. Symbolize the clues

4. Double-check your symbolizations

5. Make deductions

6. Answer the questions in the smartest order

This case will show you how to use this same method to work grouping games. The primary difference will be in how the game is set up—and, correspondingly, what your diagram looks like. Take a moment to attempt this game before you turn to the discussion and explanation that follows.

Ralph is hosting a dinner party. Because his table has limited seating, he must invite exactly four guests. He will select his guests from the following list of eight of his friends: Angelica, Brunson, Cathy, Daisuka, Finley, Grant, Helen, and Isaiah. Based on what he knows about his friends, Ralph will choose whom to invite to the party consistent with the following:

He does not invite both Angelica and Brunson.

He does not invite Grant if he invites Finley.

If he invites Angelica, he does not invite Isaiah.

If he invites Daisuka, then he also invites Angelica.

He invites either Helen or Isaiah, but he does not invite them both.

If he does not invite Cathy, he invites Grant.

1. Which of the following could be the four guests whom Ralph invites to dinner?

(A) Angelica, Brunson, Cathy, and Helen

(B) Angelica, Cathy, Daisuka, and Helen

(C) Angelica, Daisuka, Finley, and Helen

(D) Cathy, Finley, Grant, and Helen

(E) Cathy, Daisuka, Grant, and Helen

2. If Ralph invites Daisuka, then which of the following could be true?

(A) He also invites Brunson

(B) He does not invite Helen.

(C) He also invites Cathy.

(D) He does not invite Angelica.

(E) He also invites Finley.

3. If Ralph invites Brunson and Helen, then which of the following guests must he also invite?

(A) Cathy

(B) Finley

(C) Isaiah

(D) Grant

(E) Daisuka

4. Ralph could invite either Angelica or Brunson if he also invites which of the following pairs of guests?

(A) Cathy and Daisuka

(B) Cathy and Isaiah

(C) Grant and Isaiah

(D) Daisuka and Helen

(E) Grant and Helen

5. If Ralph invites Cathy, which of the following guests, if invited, would result in the guest list for the party being completely determined?

(A) Isaiah

(B) Finley

(C) Daisuka

(D) Brunson

(E) Grant

STEP 1:  Identify the Game Type

Again, to determine what type of game you’re dealing with, you look to the language in the setup and the language in the clues. This game asks you to sort the elements into two lists: those who are invited to the dinner party, and those who are not. That makes this a grouping game.

The setup of a grouping game will contain language that instructs you to “select,” “choose,” or “assign” certain elements “from” or “among” a list to a particular group, bin, or team. The setup may introduce the clues with language telling you that the clues limit the composition of each group, the formation of each team, or the assignment or selection of the elements.

In the clues, look for language that keeps elements together or forces them apart by assigning them to the same or a different group or team. Similarly, the clue might tell you that a certain team or group cannot have a particular element, must have a particular element, must have both of two elements, or must have one or the other but not both of two elements. In addition, most grouping games utilize conditional clues that tell you what happens if a certain element is included, excluded, selected, omitted, on, off, in, or out.

This game, with Ralph hosting a dinner party, is the most typical type of LSAT grouping game in two respects. First, it has only two groups. You’ll also encounter grouping games with more groups, but two-group games are much more common.

Second, the “people who are not invited” is a second, equally important group. That’s typical of two-group grouping games on the LSAT: the game tells you only that certain elements must be invited, selected, chosen, assigned, or taken. It’s left to you to create a second group.

STEP 2:  Begin Your Diagram

Create a diagram that captures the logical relationship between the game’s elements. What does this game look like?

Imagine Ralph drawing up his guest list. On one side of the list are the people he’s inviting, and on the other side are the folks who didn’t make the cut. As to each element, the game asks, “Are you invited? Yes or no?” That points the way to the beginning of a diagram:

This game provides one additional piece of information that is critical to a proper diagram: “he must invite exactly four guests.” A more difficult grouping game might leave the number of elements in each group undefined, limited only by the information in the clues. But here, we know we have two groups of equal size: four yeses, four nos; we’ll draw that fact directly into our diagram:

STEP 3:  Symbolize the Clues

Recall the general principles of symbolization discussed in Case 1. You should symbolize the clues so that they look on the page as they’ll look in the diagram. And whenever possible, symbolize clues directly into the diagram.

Clue 1: “He does not invite both Angelica and Brunson.”

This clue tells you that A and B cannot both be in the “yes” group; that means one slot in the “no” group will always be reserved for either A or B. You should symbolize this clue directly into your diagram using a placeholder in the “no” group:

That placeholder tells you that one slot in the “no” is always spoken for by either A or B.

Two-group grouping games like this one are where you’ll really reap the benefits of mastering Case 2’s discussion of conditional statements. This clue also tells you that if Ralph invites Angelica, he cannot invite Brunson:

A → ~B

and that if he invites Brunson, he cannot invite Angelica:

B → ~A

List those clues out to the side of your diagram.

Recall from Case 2 that there is a standard deduction that follows automatically from every conditional statement: its contrapositive. Any time you symbolize a conditional statement, you should immediately also symbolize its contrapositive. It’s important to get in the habit of doing this automatically. Here, that means you should also write the following out to the side of your diagram:

~A → B
~B → A

Clue 2: “He does not invite Grant if he invites Finley.”

This is a common wrinkle: a conditional clue that lists the consequence before the condition. As long as you remember that the condition is the statement that follows “if,” you’ll diagram these clues correctly:

F → ~G
G → ~F

Clue 3: “If he invites Angelica, he does not invite Isaiah.”

Clue 4: “If he invites Daisuka, then he also invites Angelica.”

These two clues are more of the same:

A → ~I, and its contrapositive:
I → ~A

D → A, and its contrapositive:
~A → ~D

Clue 5: “He invites either Helen or Isaiah, but he does not invite them both.”

This is a very useful clue because it’s actually two clues. First, it tells you that one spot in your “yes” group is always occupied by either H or I, as is one spot in your “no” group. You can use placeholders to symbolize that information directly into your diagram:

Second, this clue tells you both that if Ralph invites H, he can’t invite I, and also that if he doesn’t invite H, then he must invite I. You should also symbolize each of those conditional statements along with its contrapositive.

H → ~I, and its contrapositive:
I → ~H

~H → I, and its contrapositive:
~I → H

Clue 6: “If he does not invite Cathy, he invites Grant.”

By now the proper symbolization of this clue should be familiar:

~C → G, and
~G → C

STEP 4:  Double-Check Your Symbolizations

Translate your symbolizations into English, then verify what you come up with against the language of the clue. Once you’ve done that, you should have a setup and a list of clues that look like this:

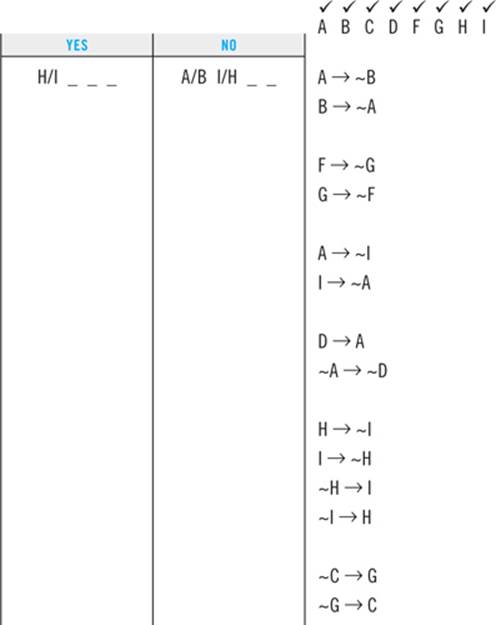
STEP 5:  Make Deductions

Recall the three types of deductions you looked for in Case 1’s ordering game in which Emily walked the dogs:

1. Can’t-be-first-or-last deductions

2. Repeated-element deductions

3. Down-to-two deductions

Since the elements don’t appear in any order, you won’t be able to make the first type of deduction.

That takes you to repeated-element deductions. This game presents an opportunity to make a particular kind of repeated-element deduction, which we’ll call conditional-combination deductions.

To make a conditional-combination deduction:

1. Look for an element that appears in the front half of one conditional clue and in the back half of another. In other words, the same element needs to be on the left side of one arrow and the right side of a different arrow.

2. Combine the statements.

For example, your list of clues for this game looks like this (the clues are numbered on this list for ease of reference):

1. A → ~B
B → ~A

2. F → ~G
G → ~F

3. A → ~I
I → ~A

4. D → A
~A → ~D

5. H → ~I
I → ~H
~H → I
~I → H

6. ~C → G
~G → C

Look at clues 6 and 2. G appears on the right side of the arrow in clue 6 (~C → G), and it appears on the left side of the arrow in the contrapositive of clue 2 (G → ~F). Therefore, you can combine those two statements to make the following deduction: ~C → G & ~F. You can add that deduction to the bottom of your list of clues.

You can make a similar deduction by combining clues 1 and 4. Take a moment to make it yourself.

The net result of B → ~A and ~A → ~D is B → ~A & ~D.

This game will support one final conditional-combination deduction, and it’s a big one: four separate clues are involved. See if you can identify which ones they are. Remember, find an element that appears on the right side of one arrow and the left side of another. Continue to repeat the process until no more combinations are available.

Here, your big deduction starts with clue 4: D → A. Clue 1 gives you A → ~B, clue 3 gives you A → ~I, and the last part of clue 5 gives you ~I → H. Put them together and you’ve got:

D → A, ~B, ~I, & H

In a two-group grouping game like this, this is an immensely valuable deduction. If D is in the “yes” group, it dramatically constrains the game; you automatically know what happens with five out of the eight elements.

At this point, the list of clues and deductions running down the side of your diagram should look like this:

CLUES

A → ~B
B → ~A
F → ~G
G → ~F
A → ~I
I → ~A
D → A
~A → ~D
H → ~I
I → ~H
~H → I
~I → H
~C → G
~G → C

DEDUCTIONS

~C → G & ~F
B → ~A & ~D
D → A, ~B, ~I, & H

That’s a lot of information to keep track of; this is one of the ways the LSAT’s writers can increase the difficulty level of a game.

No other conditional-combination deductions are available, so look now for down-to-two deductions. Two-group grouping games like this one frequently support a particular type of down-to-two deduction.

Recall clue 2: “He does not invite Grant if he invites Finley.” You symbolized that clue as:

F → ~G
G → ~F

This is a one-or-the-other clue. If Ralph invites Finley, he can’t invite Grant. If he invites Grant, he can’t invite Finley. There’s no scenario in which both F and G are in your “yes” group. That means that at least one or the other of F and G will always be in the “no” group. Make note of that fact using a placeholder:

Importantly, there’s no placeholder in the “yes” group. It would be perfectly consistent with clue 2 for both F and G to be in the “no” group.

So how do you identify a one-or-the-other clue that will support this particular kind of down-to-two deduction? To make down-to-two deductions in two-group grouping games with conditional clues, look for clues that tell you that one element must be a “yes” if the other is a “no.” In other order words, the language of the clue will track the names of the groups. You have two groups in this game: “yes” and “no.” And clue 2 tells you that if one element (F) is in “yes,” then another element (G) must be in “no.”

There is one other clue in this game that will support the same kind of deduction. Take a moment to see if you can identify it.

Clue 6 tells you that there is no scenario under which Ralph invites neither Grant nor Cathy. If Grant is a “no,” Cathy is a “yes.” If Cathy is a “no,” Grant must be a “yes.” One or the other of them must be in your “yes” group, so represent that fact with a placeholder:

There are no other down-to-two deductions available, and there are no block clues in this game, so you won’t be able to make any block-splitting deductions. That means you’re ready to turn to the questions.

STEP 6:  Answer the Questions in the Smartest Order

The way to approach the questions in a grouping game is the same as the way to approach them in an ordering game:

1. Answer the Complete and Accurate List question.

2. Answer questions that give you more information to work with.

3. Answer the remaining questions.

The Complete-and-Accurate-List Question.  Question 1 is a Complete and Accurate List question, although it might not look like one at first.

1. Which of the following could be the four guests whom Ralph invites to dinner?

(A) Angelica, Brunson, Cathy, and Helen

(B) Angelica, Cathy, Daisuka, and Helen

(C) Angelica, Daisuka, Finley, and Helen

(D) Cathy, Finley, Grant, and Helen

(E) Cathy, Daisuka, Grant, and Helen

Each answer choice is a complete list of the members of a “yes” group; correspondingly, each “no” group is made up of the four elements not listed. To answer this question, work with each of the clues one at a time. Pick a clue, then scan the answers looking for a choice that violates the rule that clue establishes. Repeat this process with all of the clues.

Here, answer A violates clue 1, answer D violates clue 2, none of the answers violates clue 3, answer E violates clue 4, none of the answers violates clue 5, and answer C violates clue 6. The down-to-two deduction you made based on clue 6 is helpful here; it makes it much easier to recognize that answer C must be eliminated because it contains neither Grant nor Cathy. As a result, the correct choice is answer B.

Questions That Give You More Information. Next up is question 2, which instructs you to plug D into the “yes” group and asks what could be true a result.

2. If Ralph invites Daisuka, then which of the following could be true?

(A) He also invites Brunson.

(B) He does not invite Helen.

(C) He also invites Cathy.

(D) He does not invite Angelica.

(E) He also invites Finley.

Reviewing your list of clues and deductions, you see that putting D in the “yes” group is the triggering condition for your biggest deduction:

D → A, ~B, ~I, & H

A and H also go in “yes,” while B and I must go to “no”:

Just by plugging in that deduction, you learn that answer choices A, B, and D can be eliminated; they all must be false.

You have only one spot open in the “yes” group, which clue 6 tells you must be filled by either G or C. None of the rest of the clues requires that last spot to be filled by G in particular or C in particular, so you know it can be either one. With your “yes” group filled, you know that F must be a “no,” along with the other of G or C:

Since F must be a “no,” answer E must be false. As the diagram illustrates, the correct answer to question 2 is answer C: it could be true that Ralph invites Cathy.

Question 3 asks who must also be invited if Brunson and Helen are invited.

3. If Ralph invites Brunson and Helen, then which of the following guests must he also invite?

(A) Cathy

(B) Finley

(C) Isaiah

(D) Grant

(E) Daisuka

The question gives you concrete new information to work with: B and H are both in the “yes” group. The first step is to plug that new information into the diagram and then combine it with the clues and deductions that also give you information about B and H. Here, clue 1 tells you that if B is a “yes,” A must be a “no,” and clue 5 tells you that if H is a “yes,” then I must be a “no.”

Scanning the answer choices, you see that you can already eliminate answer choice C. Because A is not invited, the fourth clue tells you that D must also be in the “no,” group:

That allows you to eliminate answer choice E, but that’s as far as you can go, and you don’t yet have enough information to answer the question. What next?

Unable to fill in the rest of your diagram, you have to turn to the process of elimination. But that doesn’t mean you should just grab the first answer choice you see and plug it into your diagram. That approach is time-consuming; you could end up having to diagram three or four possibilities. There’s a smarter way to eliminate answer choices. It’s based on the down-to-two concept you’re familiar with from making deductions.

The down-to-two strategy for the process of elimination works like this: If there’s any slot in your diagram that you know is restricted to two possibilities, diagram both of them. Once you do, you’ll know you’ve exhausted all of the game’s possible arrangements. That will allow you to determine what must be or what could be true.

Here, you know that the last slot in the “no” group must be occupied by either F or G. So you can draw two scenarios—one where F is a “no,” and one where G is a “no”—and be certain you’ve covered the full universe of possibilities.

If F is a “no,” that forces both G and C into the “yes” group:

Scanning through your clues, you can verify that this arrangement doesn’t violate any of the rules. Next, if G is a “no,” that forces F and C into the “yes” group:

This arrangement, too, is consistent with all the clues. This allows you to arrive at answer A as the correct answer to question 3: Ralph could invite either Finley or Grant, but he only must invite Cathy.

The last question that gives you new information is question 5.

5. If Ralph invites Cathy, which of the following guests, if invited, would result in the guest list for the party being completely determined?

(A) Isaiah

(B) Finley

(C) Daisuka

(D) Brunson

(E) Grant

This is one of the more difficult question types you’ll encounter on the Logic Games section. You want to look for answer choices that contain elements that are heavily restricted. The more information you have about an element, the more likely it is that placing that element will completely determine the game.

In this game the choice is easy. The last conditional-combination deduction you made showed you that if D is in the “yes” group, you automatically know what happens with four other elements:

D → A, ~B, ~I, & H.

In other words, if D is a “yes,” A and H must also be “yeses.” The question tells you that C also must be a “yes”—that makes four elements in the “yes” group, which completely determines the game. Consequently, the correct answer to question 5 is answer C.

If you hadn’t been able to zero in on D based on your deductions, you would have worked through the answer choices one at a time. If, after plugging in the answer, any slot in the game is not definitively filled, you would eliminate that choice and move on. There’s no faster or smarter way to tackle these kinds of questions.

The Remaining Questions. That brings you to question 4, the only question associated with this game that does not give you any new information.

4. Ralph could invite either Angelica or Brunson if he also invites which of the following pairs of guests?

(A) Cathy and Daisuka

(B) Cathy and Isaiah

(C) Grant and Isaiah

(D) Daisuka and Helen

(E) Grant and Helen

You’ll approach this question by applying the three techniques introduced in Case 1 in sequential order:

1. Can you answer this question using the clues and your deductions?

2. Can you answer this question using work you did on previous questions?

3. Can you answer this question by plugging the answer choices into your diagram?

Question 4 asks which two guests can be invited so that Ralph would still be free to invite either Angelica or Brunson. In other words, what pair of invitees makes A and B interchangeable?

First, work with the clues and your deductions. The correct answer will not contain any element that, when placed in the “yes” group, requires either A or B to be invited. Similarly, the correct answer will not contain any element that, when placed in the “yes” group, prohibits either A or B from being invited.

1. Find either A, ~A, B, or ~B as a consequence, behind the arrow.

2. Eliminate the element that is the condition.

1. A → ~B
B → ~A

2. F → ~G
G → ~F

3. A → ~I
I → ~A

4. D → A
~A → ~D

5. H → ~I
I → ~H
~H → I
~I → H

6. ~C → G
~G → C

Looking over your clues, you first come across the contrapositive of clue 3: I → ~A. If I is invited, Ralph is prohibited from inviting A. That allows you to eliminate answer choices B and C. Next up is clue 4: D → A. Since inviting D obligates Ralph to also invite A, you can eliminate answer choices A and D. By the process of elimination, you know that the correct answer must be answer choice E.

Grouping Game Setup Drills

The grouping game you just finished was not particularly easy. The fact that every single clue was a conditional statement added a substantial measure of difficulty. On the other hand, the fact that the game specified that each group had exactly four members made working it a lot easier.

There are a variety of ways that grouping games can be made more difficult. The following page contains two setup drills that are designed to introduce you to some of the variants on grouping games you might encounter on test day. Each drill contains the setup and the clues of a grouping game, but no questions. For each drill, symbolize the clues, begin your diagram, and make deductions. Answers and comments follow the games.

Drill 1

A doctor will make rounds on which she visits her patients three times today: in the morning, afternoon, and evening. She visits exactly five patients: A, B, C, D, and E. On each round she visits at least two patients, and she must visit each patient at least once. The doctor visits her patients in accordance with the following restrictions:

On each round, she visits either C or D.

She visits both C and E on exactly one of her rounds.

She visits B on exactly two of her rounds.

She does not visit A on a round unless she is not visiting either E or D.

Drill 2

A car dealer has received 10 new cars: three sedans—A, B, and C—four trucks—F, G, H, and I—and three economy models—X, Y, and Z. The dealer only has room in his showroom to display six of the cars. He must display the cars consistent with the following conditions:

He must display at least one of X or Y.

He displays exactly two trucks.

He does not display B if he displays C.

If he displays I, he also displays G.

If he displays A, he also displays Z.

DRILL 1

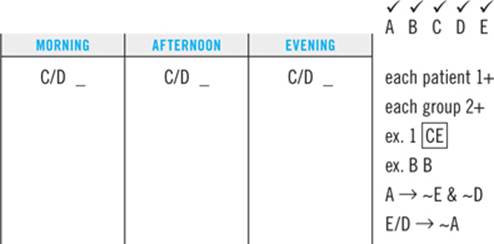
Comments. Four aspects of this game add to its difficulty:

1. Identifying the game type. At first glance, you might mistakenly identify this as an ordering game, since the doctor is visiting patients on three sequential rounds. It’s not until you read the clues (which have no “before/after” or “earlier/later” language) that it becomes clear this is a grouping game.

2. Repeated elements. Clue 3 specifies that B appears exactly twice, and the setup and the other clues leave open the possibility that the other elements also could appear two or maybe three times. That adds a degree of difficulty to the game.

3. Variable number of elements per group. The setup tells you that each group must have at least two elements, but it gives you no guidance on what the upper limit to the groups’ size is. Based on clue 4, you know that no group will have all five elements, but that’s all you know. The lack of a fixed number of elements per group also makes this game more difficult.

4. Clues that are hard to symbolize. Clues 1 and 4 are pretty standard, but clues 2 and 3 are not. You just have to find a way to notate the information they present in a way that makes sense to you (here, “exactly” has been abbreviated as “ex.”).

DRILL 2

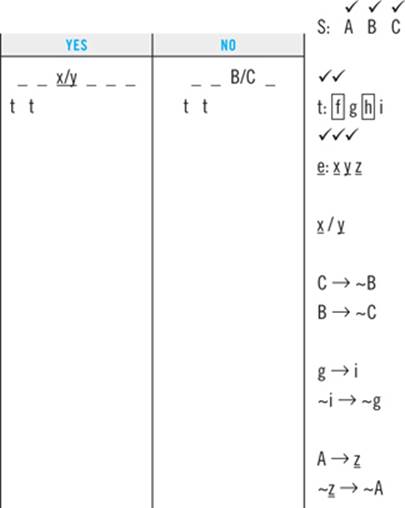
Comments. Three features of this game add to its difficulty:

1. Multiple element types. This is a common way the LSAT makes grouping games more difficult: creating multiple types, kinds, or categories of elements. When the game does that, your symbolizations should visually distinguish between the different kinds of elements: here, the diagram shows upper-case, lower-case, and underlined letters to distinguish the three kinds of automobile.

2. Sheer size. Increasing the number of elements involved in the game makes the game more difficult. It’s harder to keep track of 10 elements than it is to keep track of 6.

3. Identical elements. Two elements in this game—f and h—are free agents. Other than the fact that they are trucks, the game places no restrictions on them. They are functionally identical to each other; anything one can do, the other can do, and vice versa. That’s an easy thing to lose sight of while working a game; here, those two elements are circled as a reminder.

Two-Tiered Ordering Games: Trudy Picks Her Course Schedule

This case introduces the third major game type you’ll encounter on the Logic Games section. Games like these require you to group the elements into teams that are composed of exactly two elements. They also usually ask you to put the elements and teams in a particular order. In other words, they typically involve both the ordering task and the grouping task.

We’ll refer to these games as two-tiered ordering games. Fourteen of the last sixty published games—that’s 23 percent, almost one out of every four—have been two-tiered ordering games. You’re almost as likely to see one of these on test day as you are to see a grouping game.

As the name suggests, the best way to approach these games is to use a diagram that is derived from and very similar to the one you used to approach a one-tiered ordering game. This case introduces that setup and some of the distinctive kinds of clues two-tiered ordering games frequently utilize.

A sample two-tiered ordering game appears follows. This game has an abbreviated set of questions because you’ll use the same approach to working questions on two-tiered ordering games that you use on other types of games. The few included here are designed to help familiarize you with working with this kind of diagram. Take a moment to try to work this game on your own using the familiar six-step approach before you turn to the explanation.

Trudy is a college student who is planning her course schedule for the upcoming semester. To satisfy the requirements for graduation, she must take the following six classes: Linguistics, Macroeconomics, Oceanography, Philosophy, Rhetoric, and Sociology. She takes classes only on Mondays, Tuesdays, and Wednesdays. She takes exactly two classes per day, one at 11:00 a.m. and one at 3:00 p.m. Trudy must schedule her classes consistent with the following:

She cannot take Macroeconomics and Rhetoric on the same day.

She must take Macroeconomics and Sociology on consecutive days.

She must take Philosophy on a later day than Oceanography.

She must take Linguistics sometime after she takes Sociology.

She must take Oceanography at 11:00 a.m.

1. If Trudy takes Sociology at 11:00 a.m. on Wednesday, which one of the following must be true?

(A) She takes Macroeconomics at 11:00 a.m. on Tuesday.

(B) She takes Oceanography at 11:00 a.m. on Tuesday.

(C) She takes Philosophy at 3:00 p.m. on Tuesday.

(D) She takes Linguistics at 3:00 p.m. on Monday.

(E) She takes Rhetoric at 3:00 p.m. on Monday.

2. Which of the following cannot be the pair of classes Trudy takes at 11:00 a.m. and 3:00 p.m. Tuesday, respectively?

(A) Philosophy and Sociology

(B) Sociology and Rhetoric

(C) Rhetoric and Linguistics

(D) Linguistics and Macroeconomics

(E) Macroeconomics and Philosophy

3. If Trudy takes both Macroeconomics and Philosophy at 11:00 a.m., which of the following must be true?

(A) She takes Philosophy on Tuesday.

(B) She takes Macroeconomics on Tuesday.

(C) She takes Linguistics on Wednesday.

(D) She takes Rhetoric on Monday.

(E) She takes Oceanography on Monday.

STEP 1:  Identify the Game Type

As always, you’ll identify what type of game you’re dealing with by looking to the language in the setup and the language in the clues. Two-tiered ordering games have three linguistic hallmarks:

1. The setup and the clues will use both grouping language and ordering language.

2. The game will have you assign exactly two elements to each group.

3. The two slots in each group will be specified.

For example, the setup of this game has a clear ordering component. Trudy is taking classes in sequential order: first Monday, then Tuesday, then Wednesday, and each day her 11:00 a.m. class comes before her 3:00 p.m. class. And the clues are rife with ordering language: some classes must be taken on a later day than, consecutive days with, or sometime before other classes.

At the same time, the setup of this game tells you that you’re assigning elements (from a list of classes) to a particular group (a day of the week). And the first clue tells you that M and R can’t be assigned to the same day. Both of those instructions utilize grouping language.

The second hallmark is also clearly present: Trudy “takes exactly two classes per day.” That type of instruction is a strong indicator that this is a two-tiered ordering game.

Finally, not only does each group (day of the week) have two members, but the slots into which those members will be placed are specified: one slot is “11:00 a.m.” and the other is “3:00 p.m.” And the slots are not interchangeable, as the fifth clue makes abundantly clear. This feature of the game—two-member groups in which each member is assigned a specified slot—is also a telltale sign of a two-tiered ordering game.

One final point about identifying two-tiered ordering games. Not all two-tiered ordering games will exhibit all three of these telltale features. But as long as a game exhibits two of these three features, you should still use the two-tiered ordering setup.

For example, some games might have you assign elements into two-member groups, but the slots in the group will be interchangeable. Others will have you assign exactly two elements to each group, and the slots in the group will be specified, but there will be no ordering component to the game. You should still use the diagram introduced in this case to set up those kinds of games.

Yes, you read that right: there are situations in which you should use the two-tiered ordering setup even when the game does not involve ordering. If the game tells you that each group has two slots, and each slot is specified, the approach you’re learning in this game is the best one to use.

STEP 2:  Begin Your Diagram

What does it look like? Visualize Trudy’s calendar. The days of the week run left to right. The hours in the day proceed from top to bottom. We’ll use that image to guide the structure of our diagram:

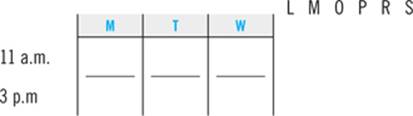
As we’ll see when we turn to symbolizing the clues, this diagram allows you to accurately capture several different kinds of logical relationships between the elements.

STEP 3:  Symbolize the Clues

Clue 1: “She cannot take Macroeconomics and Rhetoric on the same day.”

What would this clue look like? If Trudy took M and R on the same day, they would appear on top of each other in the diagram. This clue tells you that can’t happen, so you’ll add the “not” sign. And finally, you’ll use the switching arrow to convey that the clue means M and R can’t be on the same day.

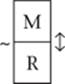
Note that this does not mean that M can’t be at 11:00 and R at 3:00 (or vice versa) on any given day.

Clue 2: “She must take Macroeconomics and Sociology on consecutive days.”

You saw a clue very similar to this one in Case 1, where Emily walked the Retriever either immediately before or immediately after the Terrier. Your first inclination might be to symbolize this clue the same way:

M ↔ S

But that symbolization could be misleading. It would be consistent with this clue for Trudy to take Macroeconomics on Tuesday afternoon and Sociology on Wednesday morning. In other words, this clue permits M and S to appear in consecutive slots, but in different tiers within those slots. You should diagram it accordingly:

Clue 3: “She must take Philosophy on a later day than Oceanography.”

This type of clue also should be familiar to you from Case 1. This time, you can use the same symbolization here that you used there, because it is an accurate representation of how this clue will look in the diagram.

O — P

Clue 4: “She must take Linguistics sometime after she takes Sociology.”

Careful—this clue is something of a trap. Take a moment to compare it to clue 3. Clue 4 permits an arrangement between L and S that clue 3 forbids between P and O. Do you see it? This clue would allow Trudy to take Sociology at 11:00 a.m. on Wednesday and Linguistics at 3:00 p.m. the same day. But clue 3 would prohibit her from taking O and P in those same time slots.

This type of clue—one that tells you only that one element must come “sometime” after the other, preserving the possibility that they could appear in the same group—is a common feature of two-tiered ordering games. And it’s not easy to diagram because there’s no single symbolization that accurately represents all the possibilities this clue allows. Both

S — L

and

are legitimate options. You can add those two options, separated by a slash (/) to indicate that either is acceptable, to your list of clues:

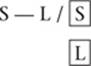
What you know definitively is that clue 4 bars both of the following two arrangements:

~(L — S)

and

You can add both of those to your list.

Clue 5: “She must take Oceanography at 11:00 a.m.”

This clue takes you back to first principles: whenever possible, symbolize a clue directly into your diagram:

STEP 4:  Double-Check Your Symbolizations

This step is the same from game to game: translate your symbolizations into English, then make sure that your translations match up with the language of each clue. Do this fully and carefully; there is no more valuable investment of time on the Logic Games section.

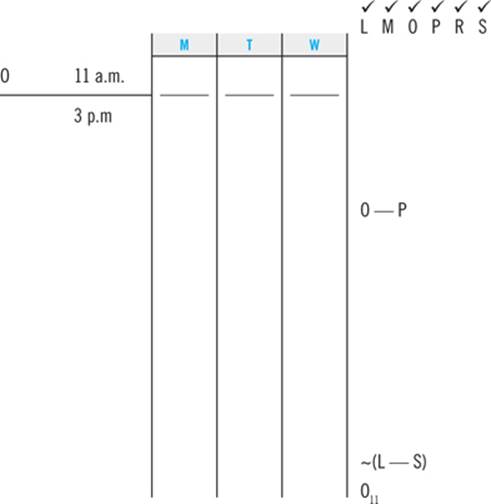
STEP 5:  Make Deductions

Two-tiered ordering games give you an opportunity to make each of the four major types of deductions:

1. Can’t-be-first-or-last deductions

2. Repeated-element deductions

3. Down-to-two deductions

4. Block-splitting deductions

In the first category, clue 2 tells you that P must come on a later day than O. That means that P can’t be on Monday, and O can’t be Wednesday:

Clue 4 tells you that S must come sometime earlier than L, so you know that S can’t be Monday at 11, and L can’t be Wednesday at 3:

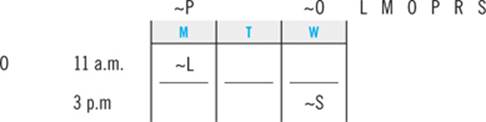
You don’t have any other before-and-after type clues, so turn to repeated-element deductions. Both M and S appear in multiple clues. But there’s no way to combine the clues. Why not? Because in each case one clue tells you what the element must do, while the other tells you what the element must not do.

Next, look for down-to-two deductions. You know from clue 5 that O must be in one of the 11:00 a.m. slots, and your deduction from clue 2 tells you that O can’t be at 11:00 a.m. on Wednesday. You can combine those two clues to determine that O must appear either at 11:00 a.m. Monday or at 11:00 a.m. Tuesday:

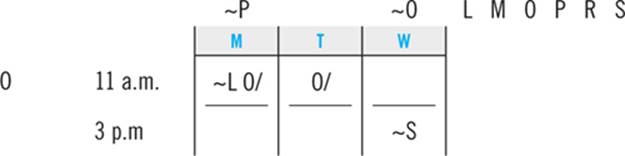
Finally, look for any block-splitting deductions:

1. Identify the blocked elements.

2. Determine where the block(s) can be placed.

3. Look for any slots where placing a single, unblocked element would split the block.

Your only block clue here is clue 3: M and S must appear on consecutive days. How could you satisfy that clue? You could place one on Monday and one on Tuesday, or one on Tuesday and one on Wednesday. And that points the way to a block-splitting deduction: no matter what, one of either M or S must be on Tuesday: if, for example, you put both O and R on Tuesday, there would no way to fill in the rest of the game that was consistent with clue 3.

Note that fact above your diagram:

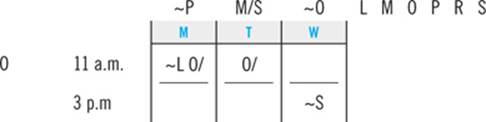
And now you’re ready to tackle the questions.

STEP 6:  Answer the Questions in the Smartest Order

As noted above, this game has an abbreviated set of questions. Since there is no Complete and Accurate List question, turn directly to the questions that give you new information. We start with question 1.

1. If Trudy takes Sociology at 11:00 a.m. on Wednesday, which one of the following must be true?

(A) She takes Macroeconomics at 11:00 a.m. on Tuesday.

(B) She takes Oceanography at 11:00 a.m. on Tuesday.

(C) She takes Philosophy at 3:00 p.m. on Tuesday.

(D) She takes Linguistics at 3:00 p.m. on Monday.

(E) She takes Rhetoric at 3:00 p.m. on Monday.

First you’ll utilize any clues that also give you information about S. Clue 4 tells you that L must come after S; there’s only one slot in the game that satisfies that requirement:

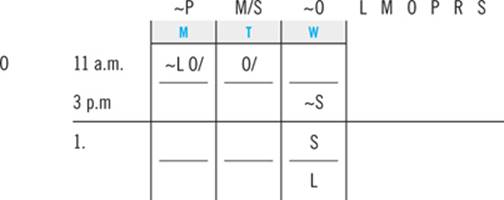
That allows you to eliminate answer choice D. Clue 3 tells you that if S is on Wednesday, then M must be sometime on Tuesday:

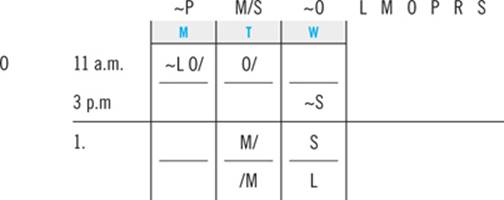
Now that you know that M must be on Tuesday, clue 1 tells you that R must be on Monday, as M and R can’t be on the same day:

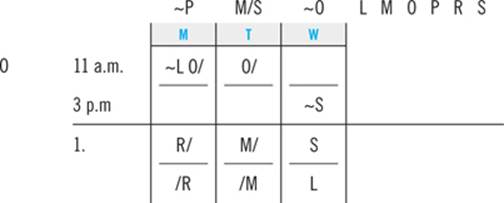
A scan of the answers reveals that you can’t select or eliminate any more choices, so you’ll keep working. All that’s left is to place P and O, and clues 2 and 5 make that relatively easy. From clue 2, you know that P must be on Tuesday and O on Monday. Clue 5 tells you that O must be Monday at 11:00 a.m., which means R must be in the afternoon. You don’t have any further information on M and P, however, so either of those elements could occupy either Tuesday slot:

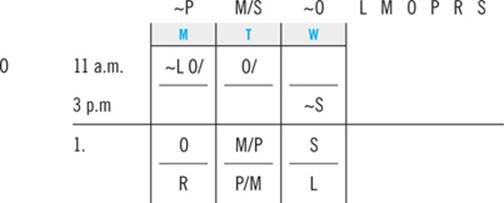
As the diagram illustrates, the correct answer to question 1 is answer E. Answers B and D must be false, while answers A and C could be, but need not, be true.

Now we’ll look at question 3.

3. If Trudy takes both Macroeconomics and Philosophy at 11:00 a.m., which of the following must be true?

(A) She takes Philosophy on Tuesday.

(B) She takes Macroeconomics on Tuesday.

(C) She takes Linguistics on Wednesday.

(D) She takes Rhetoric on Monday.

(E) She takes Oceanography on Monday.

Clue 5 tells you that O also must be at 11:00 a.m., so you now know that M, P, and O must occupy the three morning slots, while S, L, and R must be in the afternoon. What next? Although this question gives you new information, it may not be immediately apparent how to plug this new information into the diagram.

In this situation, turn to the down-to-two principle and look for an element or slot in the diagram that has only two possibilities. Once you diagram them both, you’ll know you’ve covered everything.

You know that O can go in only one of two slots, thanks to clue 2. That gives you a good place to start on this question: if you plug O into Monday and Tuesday at 11:00 a.m., you’ll have covered all your bases.

First, try O at 11:00 a.m. Tuesday. Clue 2 also tells you that P must be on Wednesday, and the question narrows that down to Wednesday at 11:00 a.m. Since the question also requires M to be in an 11:00 a.m. slot, M must be on Monday:

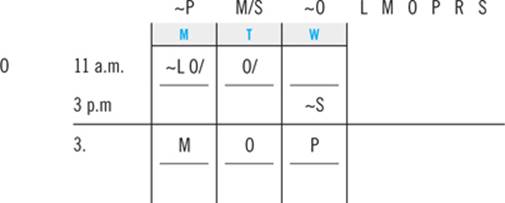
Turning to the afternoon slots, since M and S must appear on consecutive days, S must be on Tuesday afternoon. In turn, clue 4 tells you that L must be on Wednesday, which forces R into the Monday at 3:00 p.m. slot:

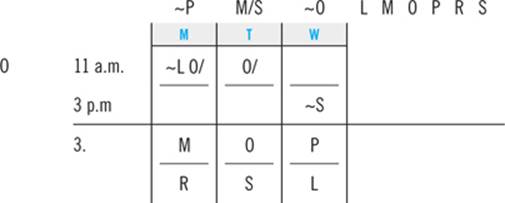
Do you see the problem with this arrangement? Clue 1 prohibits M and R from being on the same day. Therefore, O can’t be on Tuesday.

Ordinarily the next step would be to plug O into the Monday slot and continue diagramming possibilities. Fortunately, however, placing O on Tuesday allows you to identify answer choice E as the correct answer, so there’s no need to work any further. It must be true that O is in the 11:00 a.m. Monday slot.

One final note on this question: Since you’ll sometimes use prior work to eliminate answer choices on questions that don’t give you any new information, it’s important that you prominently note to yourself that this arrangement (with O on Tuesday morning) is not valid. You don’t want to inadvertently look back at it and use it to select a wrong answer on a later question. The best way to do that is to lightly cross it out:

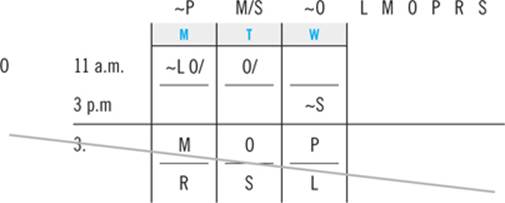
Now turn to question 2.

2. Which of the following cannot be the pair of classes Trudy takes at 11:00 a.m. and 3:00 p.m. Tuesday, respectively?

(A) Philosophy and Sociology

(B) Sociology and Rhetoric

(C) Rhetoric and Linguistics

(D) Linguistics and Macroeconomics

(E) Macroeconomics and Philosophy

On questions that give you no new information, your first step is to attempt to use your clues and deductions to eliminate or select answer choices. Here, that’s as far as you have to go. Your block-splitting deduction tells you that Trudy must take either M or S on Tuesday. Answers A and B contain S, while answers D and E contain M. Since putting both R and L on Tuesday would split the M–S block, the correct answer to question 2 is choice C.

Two-Tiered Ordering Game Setup Drills

Recall from our discussion of step 1 that two-tiered ordering games have three hallmarks, the presence of any two of which is enough to signal that you should set up the game using the diagram you learned in this case. One of the main challenges that two-tiered ordering games present is the fact that they can sometimes be difficult to identify.

Following are two setup drills of games that are harder to identify as two-tiered ordering games. Each drill contains the setup and the clues of a two-tiered ordering game, but no questions. for each drill, symbolize the clues, begin your diagram, and make deductions. Answers and comments appear after the games. Pay close attention to the language in the setup and the clues; see if you can pinpoint exactly what makes each game a two-tiered ordering game.

Drill 1

Six volleyball teammates—Maria, Nancy, Rebecca, Priscilla, Tanya, and Yvonne—are to practice on three courts: court one, court two, and court three. Each team member is assigned to a position as either a setter or a hitter. Exactly two teammates—one setter and one hitter—practice on each court. They are assigned to the courts consistent with the following:

Yvonne is a hitter.

Priscilla does not practice on court three.

Tanya and Nancy play the same position.

Priscilla practices on the same court as either Maria or Rebecca.

Drill 2

A law firm’s file clerk is placing six case files in a file cabinet: B, D, G, H, J, and K. The files will be placed in order from front to back. Each file is from a case whose status is either active or closed. The clerk organizes the files in accordance with these conditions:

Each file from an active case has a file from a closed case directly behind it.

B is an active case.

K is somewhere in front of H.

G is the fourth file in the cabinet.

The second file in the cabinet is from an active case

DRILL 1

Comment. This game has two of the three hallmarks of a two-tiered ordering game—you are assigning exactly two elements to each group, and the slots in the groups are specified—despite the fact that there is no ordering component to this game. The benefit of using this setup for a game like this is that it allows you to use blocks in diagramming both clues 3 and 4.

DRILL 2

Comments. Two points will help you solve this game.

1. Correctly identifying the game type: This is a fairly common type of two-tiered ordering game: you’re assigning elements to slots, and each of those elements has one of two particular characteristics. When you see a game like this, this is the best setup: the element in the top tier, and the characteristic in the bottom tier.

2. Making deductions based on clue 1: Two-tiered ordering games like this one almost always have a clue similar clue 1, from which you can deduce a lot of information about the second tier of the game. It’s important that you identify that this kind of clue (1) should be diagrammed as a conditional statement, and (2) will support an “if someone must be after you, you can’t be last” deduction.

“1-2-2 or 1-1-3?” Games: A Bellman Carries Bags

This case introduces the final type of game you could encounter in the Logic Games section. Games like these are relatively rare: only 10 percent of the more recently published games have been “1-2-2 or 1-1-3?” games. When they do show up, they are usually one of the more difficult games in the section. In Case 6, which will discuss strategies for working the Logic Games section as a whole, we’ll talk about ranking games by order of difficulty and working your way through the section from easiest to hardest. One of the best reasons to learn about these “1-2-2 or 1-1-3?” games is to learn how to identify them and postpone working on them until you’ve already completed the easier games.

So what exactly is a “1-2-2 or 1-1-3?” game? Like two-tiered ordering games, these games are hybrid games that involve both the ordering task and the grouping task. Unlike two-tiered ordering games, they do not assign a fixed number of slots to each group. The defining feature of a “1-2-2 or 1-1-3?” game is that instead of dictating the number of elements assigned to each group in the setup, it requires you to determine this as part of the game.

The bad news about these games is that the number of elements assigned to each group can vary from question to question. That variability adds difficulty to these games. The good news is that there is always a very small number of possibilities for how many elements there might be in each group. Typically, there are only two possible ways to distribute the elements among the groups. Hence the name we’re using to describe these games. For example, a game might list five elements, create three groups, and tell you nothing more than that each group contains at least one element. In this hypothetical game, there are only two ways to distribute the elements among the groups: 1, 2, and 2; or 1, 1, and 3. Taking the time up front to identify the different possible distributions of elements among the groups is the key to conquering these games.

A sample game of this type follows. Like the game in Case 4, this game contains only a few sample questions. Try to work this game on your own before you turn to the explanation. As you work it on your own, focus on trying to identify how many ways the elements can be distributed among the groups.

A bellman at a hotel must deliver bags to six guests of the hotel. Each bag belongs to exactly one guest: Anand, Blake, Carmina, Deanna, Eun, or Francisco. The bellman makes exactly three trips to deliver the six bags. Each bag is delivered in exactly one trip. The bellman delivers at least one and no more than three bags per trip. The bellman delivers the bags in accordance with the following conditions:

He delivers Eun’s bag at the same time he delivers either Anand’s bag or Blake’s bag, but not both.

He delivers Francisco’s bag before he delivers Eun’s bag.

He delivers Deanna’s bag before he delivers Blake’s bag.

He does not deliver Carmina’s bag before he delivers Eun’s bag.

1. If the bellman delivers Anand’s and Carmina’s bags and no others on his third trip, then which of the following must be true?

(A) He delivers exactly one bag on his first trip.

(B) He delivers exactly one bag on his second trip.

(C) He delivers exactly two bags on his second trip.

(D) He delivers exactly three bags on his first trip.

(E) He delivers exactly three bags on his second trip.

2. If the bellman delivers Anand’s bag on his first trip, which of the following must be true?

(A) He delivers Deanna’s bag on his first trip.

(B) He delivers Deanna’s bag on his second trip.

(C) He delivers Carmina’s bag on his third trip.

(D) He delivers Eun’s bag on his third trip.

(E) He delivers Francisco’s bag on his second trip.

3. If Blake’s is the only bag the bellman delivers on one of his trips, which of the following could be true?

(A) He delivers Deanna’s bag on his third trip.

(B) He delivers Carmina’s bag on his second trip.

(C) He delivers Blake’s bag on his first trip.

(D) He delivers Anand’s bag on his first trip.

(E) He delivers Francisco’s bag on his second trip.

STEP 1:  Identify the Game Type

Like a two-tiered ordering game, the setup and clues of a “1-2-2 or 1-1-3?” game will contain both ordering language and grouping language. The key difference between the two is in the number of elements that are assigned to each group, bin, or team. Instead of being fixed at exactly two, the number will vary from a required minimum of one up to a maximum of three (or—on very rare occasions—four). That combination—language that is a hybrid of ordering and grouping plus a variable number of elements per group—is the hallmark of a “1-2-2 or 1-1-3?” game.

The language the game uses to convey that combination will vary. In some games—including this one—the setup will expressly instruct that “each [group] must have at least one [element], and each [group] can hold up to three [elements].” When you see that kind of language—each group contains a minimum of one and a specified maximum of three or more—you know you’re dealing with a “1-2-2 or 1-1-3?” game.

Other times, however, these games are harder to identify. The setup might only specify that each group contains at least one element, leaving the maximum number of elements per group undefined. That, too, is a hallmark of a “1-2-2 or 1-1-3?” game, although it’s not always easy to spot. In fact, when a game involves both ordering and grouping, it’s very easy to make the mistake of assuming that it’s a two-tiered ordering game. Be mindful of this possibility.

In sum, once you recognize that a game involves both ordering and grouping, your next step should be to look at the number of elements assigned to each group. If it’s specified that each group must have exactly two elements, you’re dealing with a two-tiered ordering game. If the number of elements in each group can vary, you’re dealing with a “1-2-2 or 1-1-3?” game. Sometimes you’ll know the number of elements can vary because the game tells you that the maximum per group is more than two. Other times the game will not specify any maximum.

STEP 2:  Begin Your Diagram

A “1-2-2 or 1-1-3?” game asks you to assign elements to groups, so you’ll use the same basic diagram structure here that you used on grouping games. Here, the bellman is making three trips, so your diagram will look like this:

This game also involves ordering, though, so you might be wondering why you wouldn’t use a tiered ordering diagram similar to the one you used in Case 4 when Trudy picked her course schedule. The reason is that a tiered ordering setup can quickly become unwieldy and difficult to work with on a “1-2-2 or 1-1-3?” game. You don’t know how many tiers to put in each group, and not every group will have the same number of tiers. The traditional grouping setup can better accommodate the flexible, variable group size in “1-2-2 or 1-1-3?” games.

STEP 3:  Symbolize the Clues

Clue 1: “He delivers Eun’s bag at the same time he delivers either Anand’s bag or Blake’s bag, but not both.”

This clue is actually two clues wrapped into one. It tells you that E must be with one of two other elements, and it also tells you that E cannot be with both of those other two elements. Diagram each piece of information separately:

and also

Clue 2: “He delivers Francisco’s bag before he delivers Eun’s bag.”

Clue 3: “He delivers Deanna’s bag before he delivers Blake’s bag.”

These two clues should be familiar from your work with one-tiered and two-tiered ordering games. Diagram them the same way here that you did in those games:

F — E
D — B

These clues tell you how the elements must be ordered between the groups, not within the groups. Visually, the representation of the clue is accurate, but it is slightly more susceptible to misinterpretation. Unfortunately, there’s no better way to draw the diagram and/or symbolize the clue. This is another reason why “1-2-2 or 1-1-3?” games tend to be some of the hardest games you’ll encounter in the Logic Games section.

Clue 4: “He does not deliver Carmina’s bag before he deliver’s Eun’s bag.”

This clue is similar to one you saw in Case 4 in that it tells you only that one arrangement of the elements is impermissible:

~(C — E)

This clue creates two possibilities for how those elements can legally be arranged: C and E can be delivered at the same time, or C can be delivered after E. Again, you’ll note that using the either/or symbol:

STEP 4:  Double-Check Your Symbolizations

This step should be very familiar by now: translate your symbolizations back into English, then compare the language of your translation with the language of each clue. The result should be that your page looks like this:

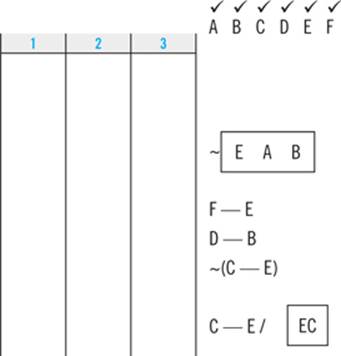
STEP 5:  Make Deductions

“1-2-2 or 1-1-3?” games require you to make a new kind of deduction in addition to the three standard deductions that you’ve already learned. On games like these, one of your core tasks is to determine how many different ways there are to distribute the elements among the groups. The first deduction you should make on a “1-2-2 or 1-1-3?” game—and these games will always support this kind of deduction—is to list out the different possible group-size combinations. You can call these group-size deductions.

Group-size deductions are a combination of the process of elimination and counting. The most systematic way to make group-size deductions is to start small and work your way up. Try to make as many groups as possible that have only one element in them. Gradually work your way down so that only one group has only one element. Then, try to have as many as you can with only two elements in them, and then three.

For example, in this game, there are three groups and six elements. Each group must contain at least one and at most three elements. So start by asking if you could possibly have two groups with exactly one element. That would force four elements into the third group, so the answer is no. What about one group with exactly one element? If you put two elements in the second group and three in the third, that works. So you know one possible arrangement: 1-2-3.

If the smallest group has two elements, the distribution is even: 2-2-2. Could the smallest group have three elements? If so, two groups would each have three elements, while the third group would have none. Since the setup tells you that each group must have at least one element, there is no legal arrangement where the smallest group has three elements.

That leaves only two possibilities for how the elements can be distributed among the groups: 1-2-3, or 2-2-2. That’s typical: most games of this type only allow two legal arrangements (on rare occasions there will be three possibilities).

Make sure you make a note of the possible arrangements somewhere on the page. Limitations on how the elements can be distributed among the groups invariably play a large role in determining the correct answers to questions on “1-2-2 or 1-1-3?” games.

Now let’s turn to the more familiar deductions.

Clues 2 and 3 both support can’t-be-first-or-last deductions:

Next, both B and E appear in multiple clues, so look for repeated-element deductions. Clues 1 and 2 will support a very straightforward deduction:

Clues 2 and 4 can also be combined. Since F must come before E, and C cannot come before E, it follows that C must come after F:

F — C

and thus also that C cannot appear in group 1:

Finally, look for down-to-two deductions. With this game, this process is quick. You can see that only three of the elements can ever end up in group 1, but you can’t narrow it down any further, so turn to the questions.

STEP 6:  Answer the Questions in the Smartest Order

This game also has an abbreviated set of questions that does not include a Complete and Accurate List question, so turn directly to the questions that give you new information.

1. If the bellman delivers Anand’s and Carmina’s bags and no others on his third trip, then which of the following must be true?

(A) He delivers exactly one bag on his first trip.

(B) He delivers exactly one bag on his second trip.

(C) He delivers exactly two bags on his second trip.

(D) He delivers exactly three bags on his first trip.

(E) He delivers exactly three bags on his second trip.

This question tells you that A and C (and no other bags) are delivered in group 3, and asks you what must be true as a result. Plug that new information into the diagram and then combine it with the clues that give you information about those two elements:

Clue 1 tells you that either A or B must be with E. Since A and C are the only elements in group 3, you know that B and E must be together in one of the first two groups. Since C is in the last group, you know that clue 4 will be satisfied no matter what you do with E.

Having exhausted the clues that give you information about the elements in the question, turn next to the remaining clues. Clue 2 tells you that F must be in an earlier group than E. Given that no additional elements can be placed in group 3, there’s only one way to satisfy clue 2:

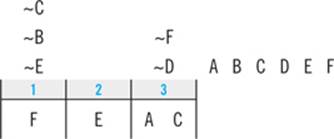
The same logic applies to clue 3, which allows you to place D and B:

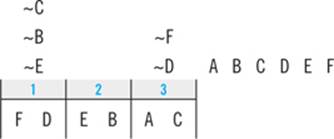
That definitively places all six elements; all six can only go in one particular group. That allows you to identify choice C as the correct answer.

2. If the bellman delivers Anand’s bag on his first trip, which of the following must be true?

(A) He delivers Deanna’s bag on his first trip.

(B) He delivers Deanna’s bag on his second trip.

(C) He delivers Carmina’s bag on his third trip.

(D) He delivers Eun’s bag on his third trip.

(E) He delivers Francisco’s bag on his second trip.

This question tells you that A is in group 1, and asks what must be true as a result.

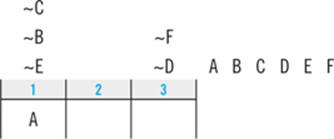
A appears in only one clue, clue 1: E has to be with either A or B. But you know from clue 2 that E can’t be in group 1. Thus, you know that E and B have to be together in one of the two later groups. Nothing in the question, the clues, or your deductions tells you which group E and B will be in, but that’s okay. You’ll use your down-to-two tactic and diagram both possibilities.

If E and B are in group 2, clues 2 and 3 require F and D to be in group 1:

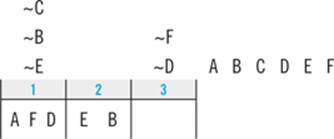
Since each group must have at least one element, C is forced into group 3. That’s consistent with clue 4, so this is a legal arrangement:

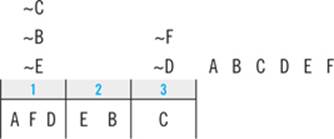
That allows you to eliminate choices B, D, and E.

If E and B are in group 3, clue 4 tells you that C must also be in group 3:

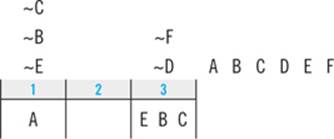
And that’s as far as you need to go to answer this question: under both scenarios, C is in group 3, and that makes choice C the correct answer to question 2.

Finally, turn to question 3.

3. If Blake’s is the only bag the bellman delivers on one of his trips, which of the following could be true?

(A) He delivers Deanna’s bag on his third trip.

(B) He delivers Carmina’s bag on his second trip.

(C) He delivers Blake’s bag on his first trip.

(D) He delivers Anand’s bag on his first trip.

(E) He delivers Francisco’s bag on his second trip.

This question tells you that B is alone in one of the groups and asks what could be true as a result. If B is alone, clue 1 tells you that E and A must be together. The question doesn’t specify which group B is alone in, but your deduction from clue 3 tells you that B can never be in group 1. Not only does that allow you to eliminate answer choice C, but you also once again find yourself down to two possibilities, so you can start diagramming.

Start by plugging B into group 2 (if you want to, you can draw a line through the rest of the space in the group as a way to remind yourself that no other elements can be there):

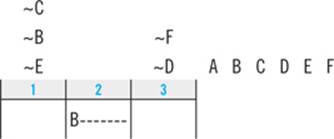
Clue 3 immediately tells you that D must be in group 1:

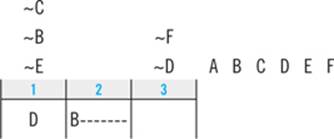
Clue 2 tells you that F must be in an earlier group than E. Since B is the only element in group 2, there is only one way to satisfy clue 2: E must be in group 3, and F must be in group 1 (your deductions above each group indicated this, too):

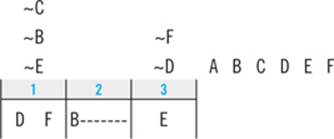
Since either A or B must be with E (clue 1), you know that A will also be in group 3:

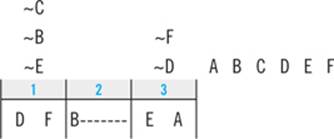
And since C cannot be delivered before E (clue 4), it too must go in group 3:

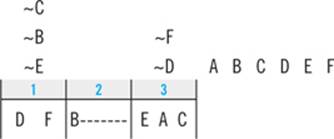
Unfortunately, this arrangement doesn’t get you a correct answer, so try the second of your down-to-two possibilities:

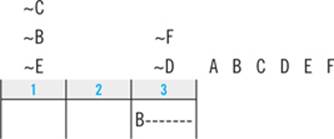
Based on clue 2, you know that F must be in group 1 and E must be in group 2:

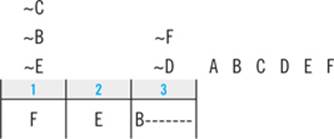
Clue 1 tells you that E and A must be together, and clue 4 tells you that C also has to be in group 2:

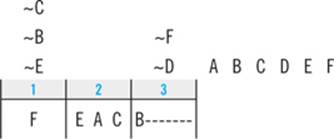
Since group 2 now has the maximum number of elements, D must be in group 1, and that’s consistent with clue 3, which is the only restriction on D’s location:

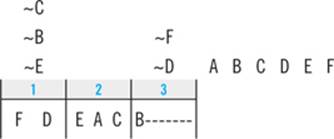
This arrangement allows you to identify choice B as the correct answer.

Conclusion

Because “1-2-2 or 1-1-3?” games appear on the LSAT so infrequently, this case does not include any setup drills with additional examples of these games. The key things to remember are the following:

1. If you see a game that (1) involves ordering and grouping, and (2) does not specify that there are two elements in each group, you’re dealing with a “1-2-2 or 1-1-3?” game.

2. Every “1-2-2 or 1-1-3?” game will support a group-size deduction.

3. If you see one of these games, it’s likely to be one of the more difficult games in the section.

Section-Wide Strategy

You’re now familiar with all four types of games that you’re likely to encounter in the Logic Games section. Below is a summary of the six-step approach you’ll use to work those games:

1. Identify the game type.

 Are you asked to put the elements in sequential order? (ordering game)

 Are you asked to assign the elements to groups? (grouping game)

 Are two of the following true: (1) You are asked to do both ordering and grouping; (2) there are exactly two slots per group; (3) the slots in the group are specified? (two-tiered ordering game)

 Are you being asked to do both ordering and grouping, but the group size is not limited to two? (“1-2-2 or 1-1-3?” game)

2. Begin your diagram.

 What does this game look like?

 Have you listed out all the elements in the game?

3. Symbolize the clues.

 Visually, what will this clue look like when it’s placed in the diagram?

4. Double-check your symbolizations.

 When you translate your symbolization back into English, does it match the language of the clue?

5. Make deductions.

 Can you make a group-size deduction? (“1-2-2 or 1-1-3?” games only)

 Can you make any can’t-be-first-or-last deductions? (not applicable in grouping games)

 Can you make any repeated-element deductions using elements that appear in more than one clue? If there are multiple conditional clues, can you make any conditional-combination deductions?

 Can you make any down-to-two deductions? Are there any one-or-the-other clues that will allow you to use placeholders?

 Can you make any block-splitting deductions?

6. Answer the questions in the smartest order.

(A) Answer the Complete and Accurate List question.

 Is this the first question associated with the game?

 Which clue does each answer choice violate?

(B) Answer questions that give you more information.

 How does this new information fit into your diagram?

(C) Answer the remaining questions.

 Can you answer this question using the clues and your deductions?

 Can you answer this question using work you did on previous questions?

 Can you answer this question using the process of elimination? Is there a place in the game that is limited to two possibilities, so that if you diagram them both you know you’ve covered all your bases?

Those six steps will enable you to work any game you encounter. The final piece of the puzzle is a strategy for tackling the Logic Games section as a whole.

There are two components to an effective section-wide Logic Games approach:

1. Work the games in the right order. You should work the easier games before you work the harder games.

2. Work the games at the right speed. You should work at the pace that maximizes your accuracy.

Accuracy Over Speed

Accuracy is more important than speed, even if being accurate means you don’t have time to work all of the questions.

Put differently, your goal is not to answer every question. Your goal is to answer as many questions correctly as you can. And the best strategy for answering questions correctly is not to hurriedly work every single question on all four games, racing to beat the 35-minute buzzer. On the contrary, most LSAT takers are better served by slowing down and concentrating their effort on fewer questions.

Consider: every Logic Games section contains four games and is 35 minutes long; most have 23 questions. Let’s say you take 32 minutes to answer the 18 questions associated with the three easiest games. Because you’re able to work carefully, you answer those questions at a 90 percent rate of accuracy. With the remaining time, you work the complete-and-accurate-list question on the final game (which, with practice, you’ll be able to answer correctly every time). You guess on the other four questions; since each question has five choices, on each question you have a 20 percent chance that your guess will be right.

On average, that strategy will net you 18 correct answers: (18 × 0.9) + 1 + (4 × 0.2) = 18. Eighteen out of twenty-three is 78 percent, which will earn you a score of around 163. That’s high enough to make you competitive for admission to virtually any law school in the country.

Work smarter, not faster. If you answer most of the questions you work correctly, you’ll get a score you’ll be happy with. With that in mind, here is the three-step approach you should use to tackle the Logic Games section as a whole:

1. Rank the games by difficulty.

2. Work the easiest game first.

3. Work the easiest questions first.

Ranking Games by Difficulty

Your goal is to work the easier games before the harder games. So what is it about a game that makes it easier or harder? As you’re scanning through the games, you should pay attention to three things:

1. What type of game is it?

2. What do the clues and the setup look like?

3. What do the questions look like?

What Type of Game Is It? The first thing you have to figure out is what kind of game you’re dealing with. As discussed in Case 5, if you see a “1-2-2 or 1-1-3?” game, it’s almost certainly one of the harder games in the section. Leave it for last.

As for the other games, keep in mind that everyone has individual strengths and weaknesses. After you’ve practiced working Logic Games for a while, you may find that grouping games give you more trouble than ordering games, or that you tend to do well on two-tiered ordering games. Incorporate that kind of personal knowledge into your decision about which games to work first.

What Do the Clues and the Setup Look Like? The test writers have a standard set of tricks they use to make each type of game more or less difficult. As you’re scanning the setup and the clues, keep an eye out for the following elements.

  Are the clues hard to understand, symbolize, and work with? You saw some examples of complex clues like these in the drills following Case 1 and Case 2. This is by far the most important thing to focus on when you’re assessing the difficulty of any kind of ordering game.

  How does the number of elements compare to the number of slots? Ideally, the numbers should be the same—that is, you’re putting six elements in order from one to six. Therefore, the easiest ordering games will say that each element is used “exactly once.” If the elements must be used “at least once” (e.g., you have to use five elements to fill eight slots) that means you’re going to be repeating elements, so the game will be a little bit trickier. If the game doesn’t specify, some elements may not be used at all (e.g., you have to fill seven slots from a group of ten elements).

  Is the number of elements in each group variable or fixed? Games where the number of elements within each group is fixed tend to be easier. Games that say you can have “up to three” elements or “at least two” elements will be harder.

  Are there multiple types of elements, or are all the elements the same? It’s typically easier to work games that involve only one kind of element. Games where the elements are divided into subcategories are more difficult, such as drill 2 of the grouping games, the one with the 10 cars that were divided into three types (sedans, trucks, economy models), which then had to be grouped into six slots.

  How big is the game? It tends to be easier to sort 6 elements into groups than it is to sort 12 elements into groups.

  How many conditional clues are there? Having all conditional clues or multiple conditional clues tends to make a game more difficult.

  Do all of the elements have to be used? On this factor, grouping games and ordering games are similar. The easiest grouping games use each element exactly once. More difficult games allow elements to be repeated or don’t require all the elements to be used.

What Do the Questions Look Like? There are three things to look for in the questions that might influence your decision about which games to work first.

1. First, how many questions give you new information? Those questions tend to be among the easiest to work. So, for example, a game with a Complete and Accurate List question, three questions that give you new information, and one other question is preferable to a game with a Complete and Accurate List question, one question that gives you new information, and three other question types, such as those that require you to rely solely on your deductions and your answers to previous questions.

2. Are there any questions associated with the game that are notoriously difficult or time-consuming? There are two question types in particular to look out for:

 Which of the following, if substituted for clue 4, would have the same effect on the composition of the game?

 Which of the following, if known, allows the order of the elements (or the composition of the groups) to be completely determined?
Each of these types of questions is difficult and time-consuming. However, that doesn’t mean that you should skip the game entirely. If the game otherwise looks good, you might work all the other questions, guess on this question, and use the time you save to work the easier questions on another game.

3. If all else fails and two games appear to be equally difficult, look to how many questions there are associated with the game. Other things being equal, a game with six questions is preferable to a game with only five.

All in all, the process of ranking the games in order of difficulty should only take you 90 seconds to two minutes. That’s not a lot of time, so you’ll necessarily be making some snap judgments. It doesn’t matter if you’re slightly off and work the second easiest game before the easiest one. The most important thing is to identify the game that is likely to give you the most trouble and work it last (if at all).