CHEMISTRY THE CENTRAL SCIENCE
12 SOLIDS AND MODERN MATERIALS
12.2 STRUCTURES OF SOLIDS
Crystalline and Amorphous Solids
Solids contain large numbers of atoms. For example, a 1-mm3 cube of NaCl contains over 2 × 1019 atoms. How can we hope to describe such a large collection of atoms? Fortunately, the structures of many solids have patterns that repeat over and over in three dimensions. We can visualize the solid as being formed by stacking a large number of small, identical structural units, much like a wall can be built by stacking identical bricks.
Solids in which atoms are arranged in an orderly repeating pattern are called crystalline solids. These solids usually have flat surfaces, or faces, that make definite angles with one another. The orderly arrangements of atoms that produce these faces also cause the solids to have highly regular shapes (![]() FIGURE 12.2). Examples of crystalline solids include sodium chloride, quartz, and diamond.
FIGURE 12.2). Examples of crystalline solids include sodium chloride, quartz, and diamond.
Amorphous solids (from the Greek words for “without form”) lack the order found in crystalline solids. At the atomic level the structures of amorphous solids are similar to the structures of liquids, but the molecules, atoms, and/or ions lack the freedom of motion they have in liquids. Amorphous solids do not have the well-defined faces and shapes of a crystal. Familiar amorphous solids are rubber, glass, and obsidian (volcanic glass).

Iron pyrite (FeS2), a crystalline solid

Obsidian (typically KAlSi3O8), an amorphous solid
![]() FIGURE 12.2 Examples of crystalline and amorphous solids. The atoms in crystalline solids repeat in an orderly, periodic fashion that leads to well-defined faces at the macroscopic level. This order is lacking in amorphous solids like obsidian (volcanic glass).
FIGURE 12.2 Examples of crystalline and amorphous solids. The atoms in crystalline solids repeat in an orderly, periodic fashion that leads to well-defined faces at the macroscopic level. This order is lacking in amorphous solids like obsidian (volcanic glass).
Unit Cells and Crystal Lattices
In a crystalline solid there is a relatively small repeating unit, called a unit cell, that is made up of a unique arrangement of atoms and embodies the structure of the solid. The structure of the crystal can be built by stacking this unit over and over in all three dimensions. Thus, the structure of a crystalline solid is defined by (a) the size and shape of the unit cell and (b) the locations of atoms within the unit cell.
The geometrical pattern of points on which the unit cells are arranged is called a crystal lattice. The crystal lattice is, in effect, an abstract (that is, not real) scaffolding for the crystal structure. We can imagine forming the entire crystal structure by first building the scaffolding and then filling in each unit cell with the same atom or group of atoms.
Before describing the structures of solids, we need to understand the properties of crystal lattices. It's useful to begin with two-dimensional lattices because they are simpler to visualize than three-dimensional ones. ![]() FIGURE 12.3 shows a two-dimensional array of lattice points. Each lattice point has an identical environment. The positions of the lattice points are defined by the lattice vectors a and b. Beginning from any lattice point it is possible to move to any other lattice point by adding together whole-number multiples of the two lattice vectors.*
FIGURE 12.3 shows a two-dimensional array of lattice points. Each lattice point has an identical environment. The positions of the lattice points are defined by the lattice vectors a and b. Beginning from any lattice point it is possible to move to any other lattice point by adding together whole-number multiples of the two lattice vectors.*
The parallelogram formed by the lattice vectors, the shaded region in Figure 12.3, defines the unit cell. In two dimensions the unit cells must tile, or fit together in space, in such a way that they completely cover the area of the lattice with no gaps. In three dimensions the unit cells must stack together to fill all space.
In a two-dimensional lattice, the unit cells can take only one of the four shapes shown in ![]() FIGURE 12.4. The most general type of lattice is the oblique lattice. In this lattice, the lattice vectors are of different lengths and the angle γ between them is of arbitrary size, which makes the unit cell an arbitrarily shaped parallelogram. A square lattice results when the lattice vectors are equal in length and perpendicular to each other. If the two vectors are perpendicular to each other but of different lengths, a rectangular lattice is formed. The fourth type of two-dimensional lattice, where a and b are the same length and γ is 120°, is a hexagonal lattice.† The lattices in Figure 12.4 represent tiling of four basic shapes: squares, rectangles, hexagons, and arbitrary parallelograms. Other polygons, such as pentagons, cannot cover space without leaving gaps, as
FIGURE 12.4. The most general type of lattice is the oblique lattice. In this lattice, the lattice vectors are of different lengths and the angle γ between them is of arbitrary size, which makes the unit cell an arbitrarily shaped parallelogram. A square lattice results when the lattice vectors are equal in length and perpendicular to each other. If the two vectors are perpendicular to each other but of different lengths, a rectangular lattice is formed. The fourth type of two-dimensional lattice, where a and b are the same length and γ is 120°, is a hexagonal lattice.† The lattices in Figure 12.4 represent tiling of four basic shapes: squares, rectangles, hexagons, and arbitrary parallelograms. Other polygons, such as pentagons, cannot cover space without leaving gaps, as ![]() FIGURE 12.5 shows.
FIGURE 12.5 shows.
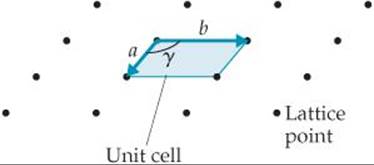
![]() FIGURE 12.3 A crystalline lattice in two dimensions. An infinite array of lattice points is generated by adding together the lattice vectors a and b. The unit cell is a parallelogram defined by the lattice vectors.
FIGURE 12.3 A crystalline lattice in two dimensions. An infinite array of lattice points is generated by adding together the lattice vectors a and b. The unit cell is a parallelogram defined by the lattice vectors.
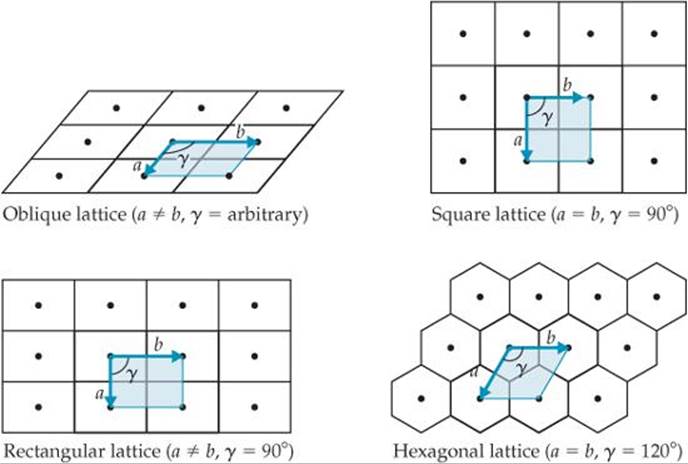
![]() FIGURE 12.4 The four two-dimensional lattices. The unit cell for each lattice is shaded.
FIGURE 12.4 The four two-dimensional lattices. The unit cell for each lattice is shaded.
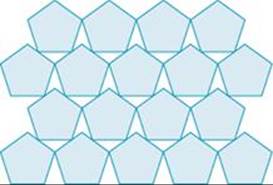
![]() FIGURE 12.5 Not all shapes tile space. Tiling means covering a surface entirely, which is impossible for some geometric shapes, as shown here for pentagons.
FIGURE 12.5 Not all shapes tile space. Tiling means covering a surface entirely, which is impossible for some geometric shapes, as shown here for pentagons.
To understand real crystals, we must move from two dimensions to three. In three dimensions, a lattice is defined by three lattice vectors a, b, and c (![]() FIGURE 12.6). These lattice vectors define a unit cell that is a parallelepiped (a six-sided figure whose faces are all parallelograms) and is described by the lengths a, b, c of the cell edges and the angles α β, γ between these edges. There are seven possible shapes for a three-dimensional unit cell, as shown in Figure 12.6.
FIGURE 12.6). These lattice vectors define a unit cell that is a parallelepiped (a six-sided figure whose faces are all parallelograms) and is described by the lengths a, b, c of the cell edges and the angles α β, γ between these edges. There are seven possible shapes for a three-dimensional unit cell, as shown in Figure 12.6.
![]() GIVE IT SOME THOUGHT
GIVE IT SOME THOUGHT
Imagine you generate a three-dimensional lattice by taking a and b vectors that form a two-dimensional square lattice. Then add a third vector, c, that is of different length and perpendicular to the first two. Which of the seven three-dimensional lattices results?
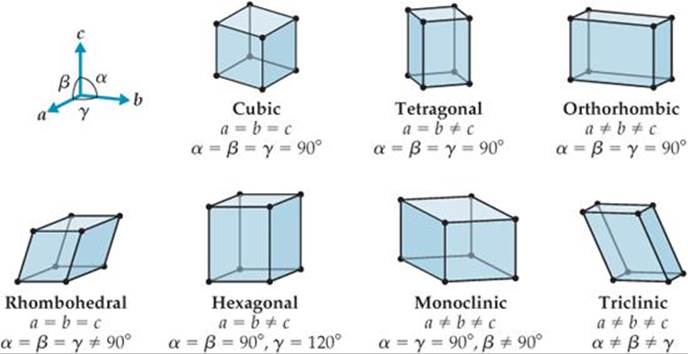
![]() FIGURE 12.6 The seven three-dimensional primitive lattices.
FIGURE 12.6 The seven three-dimensional primitive lattices.
If we place a lattice point at each corner of a unit cell, we get a primitive lattice. All seven lattices in Figure 12.6 are primitive lattices. It is also possible to generate what are called centered lattices by placing additional lattice points in specific locations in the unit cell. This is illustrated for a cubic lattice in ![]() FIGURE 12.7. A body-centered cubic lattice has one lattice point at the center of the unit cell in addition to the lattice points at the eight corners. A face-centered cubic lattice has one lattice point at the center of each of the six faces of the unit cell in addition to the lattice points at the eight corners. Centered lattices exist for other types of unit cells as well. Examples include body-centered tetragonal and face-centered orthorhombic. Counting all seven primitive lattices as well as the various types of centered lattices, there are a total of 14 three-dimensional lattices. For the crystals discussed in this chapter we need only consider the lattices shown in Figures 12.6 and 12.7.
FIGURE 12.7. A body-centered cubic lattice has one lattice point at the center of the unit cell in addition to the lattice points at the eight corners. A face-centered cubic lattice has one lattice point at the center of each of the six faces of the unit cell in addition to the lattice points at the eight corners. Centered lattices exist for other types of unit cells as well. Examples include body-centered tetragonal and face-centered orthorhombic. Counting all seven primitive lattices as well as the various types of centered lattices, there are a total of 14 three-dimensional lattices. For the crystals discussed in this chapter we need only consider the lattices shown in Figures 12.6 and 12.7.
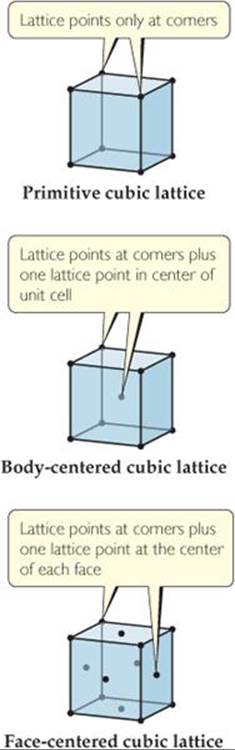
![]() FIGURE 12.7 The three types of cubic lattices.
FIGURE 12.7 The three types of cubic lattices.
Filling the Unit Cell
The lattice by itself does not define a crystal structure. To generate a crystal structure, we need to associate an atom or group of atoms with each lattice point. In the simplest case, the crystal structure consists of identical atoms, and each atom lies directly on a lattice point. When this happens, the crystal structure and the lattice points have identical patterns. Many metallic elements adopt such structures, as we will see in Section 12.3. Keep in mind that only elements can form structures of this type. For compounds, even if we were to put an atom on every lattice point, the points would not be identical because the atoms are not all of the same.
In most crystals the atoms are not exactly coincident with the lattice points. Instead, a group of atoms, called a motif, is associated with each lattice point. The unit cell contains a specific motif of atoms, and the crystal structure is built up by repeating the unit cell over and over. This process is illustrated in ![]() FIGURE 12.8 for a two-dimensional crystal based on a hexagonal unit cell and a two-carbon-atom motif. The resulting infinite two-dimensional honeycomb structure is a two-dimensional crystal called graphene. Each carbon atom is covalently bonded to three neighboring carbon atoms in what amounts to an infinite sheet of interconnected hexagonal rings.
FIGURE 12.8 for a two-dimensional crystal based on a hexagonal unit cell and a two-carbon-atom motif. The resulting infinite two-dimensional honeycomb structure is a two-dimensional crystal called graphene. Each carbon atom is covalently bonded to three neighboring carbon atoms in what amounts to an infinite sheet of interconnected hexagonal rings.
The crystal structure of graphene illustrates two important characteristics of crystals. First, we see that no atoms lie on the lattice points. While most of the structures we discuss in this chapter do have atoms on the lattice points, there are many examples, like graphene, where this is not the case. Thus, to build up a structure you must know the location and orientation of the atoms in the motif with respect to the lattice points. Second, we see that bonds can be formed between atoms in neighboring unit cells. This happens in many crystals, particularly metallic, ionic, and network-covalent solids.
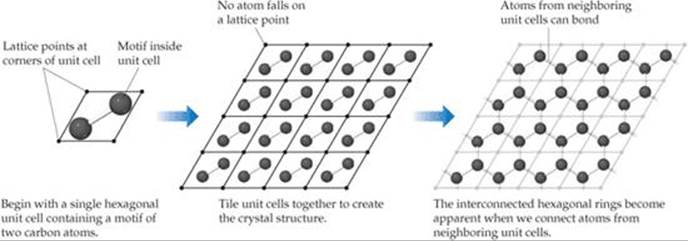
![]() FIGURE 12.8 Two-dimensional structure of graphene built up from a single unit cell.
FIGURE 12.8 Two-dimensional structure of graphene built up from a single unit cell.
 A CLOSER LOOK
A CLOSER LOOK
X-RAY DIFFRACTION
When light waves pass through a narrow slit, they are scattered in such a way that the wave seems to spread out. This physical phenomenon is called diffraction. When light passes through many evenly spaced narrow slits (a diffraction grating), the scattered waves interact to form a series of bright and dark bands, known as a diffraction pattern. The bright bands correspond to constructive overlapping of the light waves, and the dark bands correspond to destructive overlapping of the light waves (Section 9.8, “A Closer Look: Phases in Atomic and Molecular Orbitals”). The most effective diffraction of light occurs when the wavelength of the light and the width of the slits are similar in magnitude.
The spacing of the layers of atoms in solid crystals is usually about 2-20 Å. The wavelengths of X-rays are also in this range. Thus, a crystal can serve as an effective diffraction grating for X-rays. X-ray diffraction results from the scattering of X-rays by a regular arrangement of atoms, molecules, or ions. Much of what we know about crystal structures has been obtained by looking at the diffraction patterns that result when X-rays pass through a crystal, a technique known as X-ray crystallography. As shown in ![]() FIGURE 12.9 a monochromatic beam of X-rays is passed through a crystal. The diffraction pattern that results is recorded. For many years the diffracted X-rays were detected by photographic film. Today, crystallographers use an array detector, a device analogous to that used in digital cameras, to capture and measure the intensities of the diffracted rays.
FIGURE 12.9 a monochromatic beam of X-rays is passed through a crystal. The diffraction pattern that results is recorded. For many years the diffracted X-rays were detected by photographic film. Today, crystallographers use an array detector, a device analogous to that used in digital cameras, to capture and measure the intensities of the diffracted rays.
The pattern of spots on the detector in Figure 12.9 depends on the particular arrangement of atoms in the crystal. The spacing and symmetry of the bright spots, where constructive interference occurs, provide information about the size and shape of the unit cell. The intensities of the spots provide information that can be used to determine the locations of the atoms within the unit cell. When combined, these two pieces of information give the atomic structure that defines the crystal.
X-ray crystallography is used extensively to determine the structures of molecules in crystals. The instruments used to measure X-ray diffraction, known as X-ray diffractometers, are now computer controlled, making the collection of diffraction data highly automated. The diffraction pattern of a crystal can be determined very accurately and quickly (sometimes in a matter of hours), even though thousands of diffraction spots are measured. Computer programs are then used to analyze the diffraction data and determine the arrangement and structure of the molecules in the crystal. X-ray diffraction is an important technique in industries ranging from steel and cement manufacture to pharmaceuticals.
RELATED EXERCISES: 12.105, 12.106, 12.107
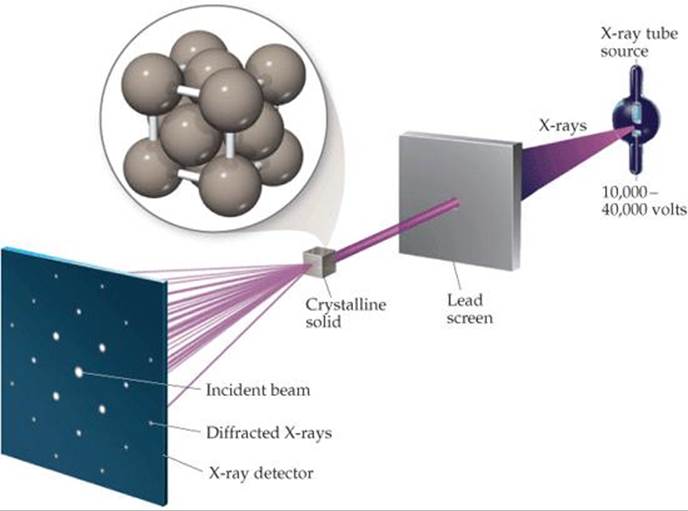
![]() FIGURE 12.9 Diffraction of X-rays by a crystal. In X-ray crystallography a monochromatic X-ray beam is passed through a crystal. The X-rays are diffracted, and the resulting interference pattern is recorded. The crystal is rotated and another diffraction pattern recorded. Analysis of many diffraction patterns gives the positions of the atoms in the crystal.
FIGURE 12.9 Diffraction of X-rays by a crystal. In X-ray crystallography a monochromatic X-ray beam is passed through a crystal. The X-rays are diffracted, and the resulting interference pattern is recorded. The crystal is rotated and another diffraction pattern recorded. Analysis of many diffraction patterns gives the positions of the atoms in the crystal.