CHEMISTRY THE CENTRAL SCIENCE
16 ACID–BASE EQUILIBRIA
16.7 WEAK BASES
Many substances behave as weak bases in water. Weak bases react with water, abstracting protons from H2O, thereby forming the conjugate acid of the base and OH– ions:
The equilibrium-constant expression for this reaction can be written as
Water is the solvent, so it is omitted from the equilibrium-constant expression. The most commonly encountered weak base is ammonia:
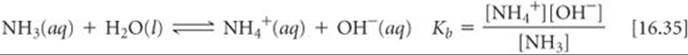
As with Kw and Ka, the subscript b in Kb denotes that the equilibrium constant refers to a particular type of reaction, namely the ionization of a weak base in water. The constant Kb, the base-dissociation constant, always refers to the equilibrium in which a base reacts with H2O to form the corresponding conjugate acid and OH–.
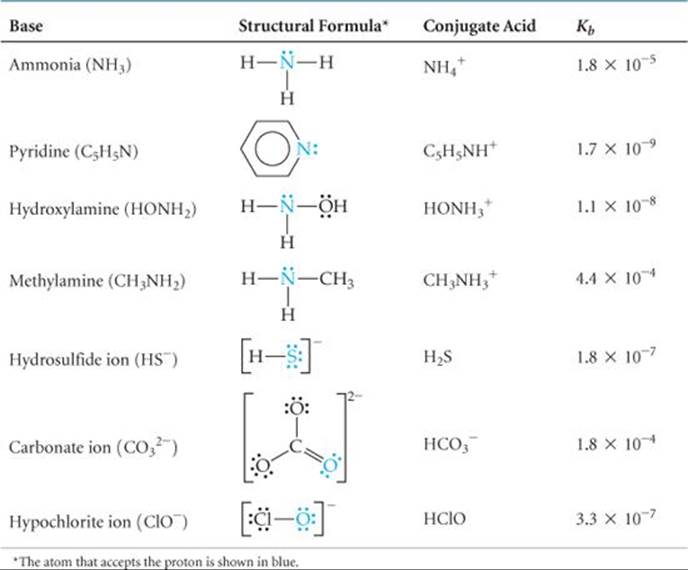
TABLE 16.4 lists the Lewis structures, conjugate acids, and Kb values for a number of weak bases in water. Appendix D includes a more extensive list. These bases contain one or more lone pairs of electrons because a lone pair is necessary to form the bond with H+. Notice that in the neutral molecules in Table 16.4, the lone pairs are on nitrogen atoms. The other bases listed are anions derived from weak acids.
TABLE 16.4 • Some Weak Bases in Water at 25 °C
SAMPLE EXERCISE 16.15 Using Kb To Calculate OH–
Calculate the concentration of OH– in a 0.15 M solution of NH3.
SOLUTION
Analyze We are given the concentration of a weak base and asked to determine the concentration of OH–.
Plan We will use essentially the same procedure here as used in solving problems involving the ionization of weak acids, that is, write the chemical equation and tabulate initial and equilibrium concentrations.
Solve The ionization reaction and equilibrium-constant expression are
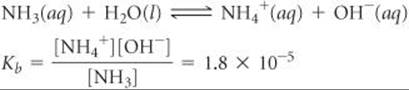
The equilibrium concentrations are (We ignore the concentration of H2O because it is not involved in the equilibrium-constant expression.)
Inserting these quantities into the equilibrium-constant expression gives
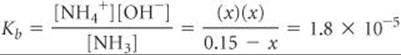
Because Kb is small, the amount of NH3 that reacts with water is much smaller than the NH3 concentration, and so we can neglect x relative to 0.15 M. Then we have
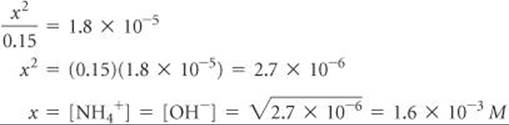
Check The value obtained for x is only about 1% of the NH3 concentration, 0.15 M. Therefore, neglecting x relative to 0.15 was justified.
Comment You may be asked to find the pH of a solution of a weak base. Once you have found [OH–], you can proceed as in Sample Exercise 16.9, where we calculated the pH of a strong base. In the present sample exercise, we have seen that the 0.15 M solution of NH3 contains [OH–] = 1.6 × 10–3M. Thus, pOH = –log(1.6 × 10–3) = 2.80, and pH = 14.00 – 2.80 = 11.20. The pH of the solution is above 7 because we are dealing with a solution of a base.
PRACTICE EXERCISE
Which of the following compounds should produce the highest pH as a 0.05 M solution: pyridine, methylamine, or nitrous acid?
Answer: methylamine (because it has the larger Kb value of the two amine bases in the list)
Types of Weak Bases
Weak bases fall into two general categories. The first category is neutral substances that have an atom with a nonbonding pair of electrons that can accept a proton. Most of these bases, including all uncharged bases in Table 16.4, contain a nitrogen atom. These substances include ammonia and a related class of compounds called amines (
FIGURE 16.13). In organic amines, at least one N—H bond in NH3 is replaced with an N—C bond. Like NH3, amines can abstract a proton from a water molecule by forming an N—H bond, as shown here for methylamine:
GO FIGURE
When hydroxylamine acts as a base, which atom accepts the proton?
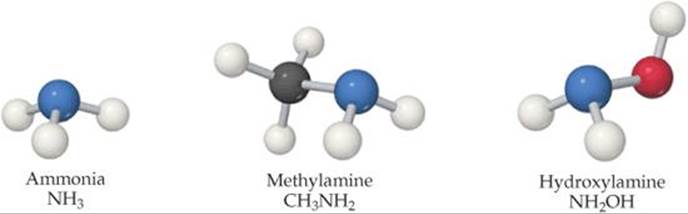
FIGURE 16.13 Structures of ammonia and two simple amines.
Anions of weak acids make up the second general category of weak bases. In an aqueous solution of sodium hypochlorite (NaClO), for example, NaClO dissociates to Na+ and ClO– ions. The Na+ ion is always a spectator ion in acid–base reactions. 
(Section 4.3) The ClO– ion, however, is the conjugate base of a weak acid, hypochlorous acid. Consequently, the ClO– ion acts as a weak base in water:
In Figure 16.5 we saw that bleach is quite basic (pH values of 12–13). Common chlorine bleach is typically a 5% NaOCl solution.
SAMPLE EXERCISE 16.16 Using pH to Determine the Concentration of a Salt
A solution made by adding solid sodium hypochlorite (NaClO) to enough water to make 2.00 L of solution has a pH of 10.50. Using the information in Equation 16.37, calculate the number of moles of NaClO added to the water.
SOLUTION
Analyze NaClO is an ionic compound consisting of Na+ and ClO– ions. As such, it is a strong electrolyte that completely dissociates in solution into Na+, a spectator ion, and ClO– ion, a weak base with Kb = 3.3 × 10–7 (Equation 16.37). Given this information we must calculate the number of moles of NaClO needed to raise the basicity of 2.00-L of water to 10.50.
Plan From the pH, we can determine the equilibrium concentration of OH–. We can then construct a table of initial and equilibrium concentrations in which the initial concentration of ClO– is our unknown. We can calculate [ClO–] using the expression for Kb.
Solve We can calculate [OH–] by using either Equation 16.16 or Equation 16.20; we will use the latter method here:
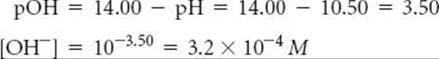
This concentration is high enough that we can assume that Equation 16.37 is the only source of OH–; that is, we can neglect any OH– produced by the autoionization of H2O. We now assume a value of x for the initial concentration of ClO– and solve the equilibrium problem in the usual way.
We now use the expression for the base-dissociation constant to solve for x:
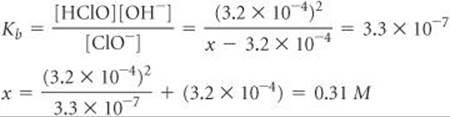
We say that the solution is 0.31 M in NaClO even though some of the ClO– ions have reacted with water. Because the solution is 0.31 M in NaClO and the total volume of solution is 2.00 L, 0.62 mol of NaClO is the amount of the salt that was added to the water.
PRACTICE EXERCISE
What is the molarity of an aqueous NH3 solution that has a pH of 11.17?
Answer: 0.12 M