CHEMISTRY THE CENTRAL SCIENCE

19 CHEMICAL THERMODYNAMICS

19.2 ENTROPY AND THE SECOND LAW OF THERMODYNAMICS

How can we use the fact that any spontaneous process is irreversible to make predictions about the spontaneity of an unfamiliar process? Understanding spontaneity requires us to examine the thermodynamic quantity called entropy, which was first mentioned in Section 13.1. In general, entropy is associated either with the extent of randomness in a system or with the extent to which energy is distributed among the various motions of the molecules of the system. In this section we consider how we can relate entropy changes to heat transfer and temperature. Our analysis will bring us to a profound statement about spontaneity that we call the second law of thermodynamics.

Entropy Change

The entropy, S, of a system is a state function just like internal energy, E, and enthalpy, H. As with these other quantities, the value of S is a characteristic of the state of a system. (Section 5.2) Thus, the change in entropy, ΔS, in a system depends only on the initial and final states of the system and not on the path taken from one state to the other:

For the special case of an isothermal process, ΔS is equal to the heat that would be transferred if the process were reversible, q_rev, divided by the absolute temperature at which the process occurs:

Although there are many possible paths that can take the system from one state to another, only one path is associated with a reversible process. Thus, the value of q_rev is uniquely defined for any two states of the system. Because S is a state function, we can use Equation 19.2 to calculate ΔSfor any isothermal process between states, not just the reversible one.

GIVE IT SOME THOUGHT

How do we reconcile the fact that S is a state function but ΔS depends on q, which is not a state function?

ΔS for Phase Changes

The melting of a substance at its melting point and the vaporization of a substance at its boiling point are isothermal processes. (Section 11.4) Consider the melting of ice. At 1 atm pressure, ice and liquid water are in equilibrium at 0 °C. Imagine melting 1 mol of ice at 0 °C, 1 atm to form 1 mol of liquid water at 0 °C, 1 atm. We can achieve this change by adding a certain amount of heat to the system from the surroundings: q = ΔH_fusion. Now imagine that we add the heat infinitely slowly, raising the temperature of the surroundings only infinitesimally above 0 °C. When we make the change in this fashion, the process is reversible because we can reverse it by infinitely slowly removing the same amount of heat, ΔH_fusion, from the system, using immediate surroundings that are infinitesimally below 0 °C. Thus, q_rev = ΔH_fusion for the melting of ice at T = 0 °C = 273 K.

The enthalpy of fusion for H₂O is ΔH_fusion = 6.01 kJ/mol (a positive value because melting is an endothermic process). Thus, we can use Equation 19.2 to calculate ΔS_fusion for melting 1 mol of ice at 273 K:

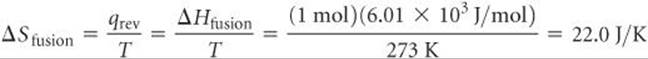
Notice (a) that we must use the absolute temperature in Equation 19.2 and (b) that the units for ΔS, J/K, are energy divided by absolute temperature, as we expect from Equation 19.2.

SAMPLE EXERCISE 19.2 Calculating ΔS for a Phase Change

Elemental mercury is a silver liquid at room temperature. Its normal freezing point is –38.9 °C, and its molar enthalpy of fusion is ΔH_fusion = 2.29 kJ/mol. What is the entropy change of the system when 50.0 g of Hg(l) freezes at the normal freezing point?

SOLUTION

Analyze We first recognize that freezing is an exothermic process, which means heat is transferred from system to surroundings and q < 0. The enthalpy of fusion refers to the process of melting. Because freezing is the reverse of melting, the enthalpy change that accompanies the freezing of 1 mol of Hg is –ΔH_fusion = –2.29 kJ/mol.

Plan We can use – ΔH_fusion and the atomic weight of Hg to calculate q for freezing 50.0 g of Hg. Then we use this value of q as q_rev in Equation 19.2 to determine ΔS for the system.

Solve

For q we have

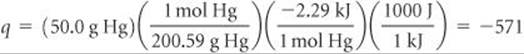
Before using Equation 19.2, we must first convert the given Celsius temperature to kelvins:

We can now calculate ΔS_sys:

Check The entropy change is negative because our q_rev value is negative, which it must be because heat flows out of the system in this exothermic process.

Comment This procedure can be used to calculate ΔS for other isothermal phase changes, such as the vaporization of a liquid at its boiling point.

PRACTICE EXERCISE

The normal boiling point of ethanol, C₂H₅OH, is 78.3 °C, and its molar enthalpy of vaporization is 38.56 kJ/mol. What is the change in entropy in the system when 68.3 g of C₂H₅OH(g) at 1 atm condenses to liquid at the normal boiling point?

Answer: –163 J/K

A CLOSER LOOK
THE ENTROPY CHANGE WHEN A GAS EXPANDS ISOTHERMALLY

In general, the entropy of any system increases as the system becomes more random or more spread out. Thus, we expect the spontaneous expansion of a gas to result in an increase in entropy. To see how this entropy increase can be calculated, consider the expansion of an ideal gas that is initially constrained by a piston, as in the rightmost part of Figure 19.5. Imagine that we allow the gas to undergo a reversible isothermal expansion by infinitesimally decreasing the external pressure on the piston. The work done on the surroundings by the reversible expansion of the system against the piston can be calculated with the aid of calculus (we do not show the derivation):

In this equation, n is the number of moles of gas, R is the gas constant (Section 10.4), T is the absolute temperature, V₁ is the initial volume, and V₂ is the final volume. Notice that if V₂> V₁, as it must be in our expansion, then w_rev< 0, meaning that the expanding gas does work on the surroundings.

One characteristic of an ideal gas is that its internal energy depends only on temperature, not on pressure. Thus, when an ideal gas expands isothermally, ΔE = 0. Because ΔE = q_rev + w_rev = 0, we see that q_rev = — w_rev = nRT ln(V₂/V₁). Then, using Equation 19.2, we can calculate the entropy change in the system:

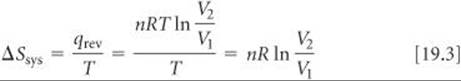
From the ideal-gas equation, we can calculate the number of moles in 1.00 L of an ideal gas at 1.00 atm and 0 °C by using the value 0.08206 L-atm/mol-K for R:

The gas constant, R, can also be expressed as 8.314 J/mol-K (Table 10.2), and this is the value we must use in Equation 19.3 because we want our answer to be expressed in terms of J rather than in L-atm. Thus, for the expansion of the gas from 1.00 L to 2.00 L, we have

In Section 19.3 we will see that this increase in entropy is a measure of the increased randomness of the molecules because of the expansion.

RELATED EXERCISES: 19.29, 19.30, and 19.106

The Second Law of Thermodynamics

The key idea of the first law of thermodynamics is that energy is conserved in any process. (Section 5.2) Entropy, however, is not conserved. For any spontaneous process, the total change in entropy, which is the sum of the entropy change of the system plus the entropy change of the surroundings, is greater than zero.

Let's illustrate this generalization by calculating the entropy change of a system and the entropy change of its surroundings when our system is 1 mol of ice (a piece roughly the size of an ice cube) melting in the palm of your hand, which is part of the surroundings. The process is not reversible because the system and surroundings are at different temperatures. Nevertheless, because ΔS is a state function, its value is the same regardless of whether the process is reversible or irreversible. We calculated the entropy change of the system just before Sample Exercise 19.2:

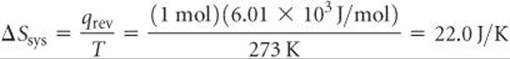
The surroundings immediately in contact with the ice are your hand, which we assume is at body temperature, 37 °C = 310 K. The quantity of heat lost by your hand is –6.01 × 10³ J/mol, which is equal in magnitude to the quantity of heat gained by the ice but has the opposite sign. Hence, the entropy change of the surroundings is

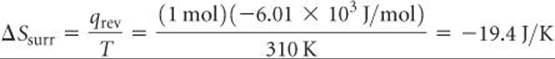
Thus, the total entropy change is positive:

If the temperature of the surroundings were not 310 K but rather some temperature in-finitesimally above 273 K, the melting would be reversible instead of irreversible. In that case the entropy change of the surroundings would equal –22.0 J/K and ΔS_total would be zero.

In general, any irreversible process results in an increase in total entropy, whereas any reversible process results in no overall change in entropy. This statement is known as the second law of thermodynamics.

The sum of the entropy of a system plus the entropy of the surroundings is everything there is, and so we refer to the total entropy change as the entropy change of the universe, ΔS_univ. We can therefore state the second law of thermodynamics in terms of two equations:

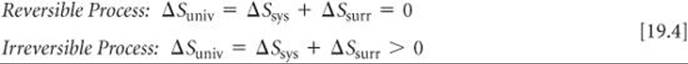
Because spontaneous processes are irreversible, we can say that the entropy of the universe increases in any spontaneous process. This profound generalization is yet another way of expressing the second law of thermodynamics.

GIVE IT SOME THOUGHT

The rusting of iron is spontaneous and is accompanied by a decrease in the entropy of the system (the iron and oxygen). What can we conclude about the entropy change of the surroundings?

The second law of thermodynamics tells us the essential character of any spontaneous change—it is always accompanied by an increase in the entropy of the universe. We can use this criterion to predict whether a given process is spontaneous or not. Before seeing how this is done, however, we will find it useful to explore entropy from a molecular perspective.

A word on notation before we proceed. Throughout most of the remainder of this chapter, we will focus on systems rather than surroundings. To simplify the notation, we will usually refer to the entropy change of the system as ΔS rather than explicitly indicating ΔS_sys.