CHEMISTRY THE CENTRAL SCIENCE

3 STOICHIOMETRY: CALCULATIONS WITH CHEMICAL FORMULAS AND EQUATIONS

3.4 AVOGADRO'S NUMBER AND THE MOLE

Even the smallest samples we deal with in the laboratory contain enormous numbers of atoms, ions, or molecules. For example, a teaspoon of water (about 5 mL) contains 2 × 10²³ water molecules, a number so large it almost defies comprehension. Chemists therefore have devised a counting unit for describing such large numbers of atoms or molecules.

In everyday life we use such familiar counting units as dozen (12 objects) and gross (144 objects). In chemistry the counting unit for numbers of atoms, ions, or molecules in a laboratory-size sample is the mole, abbreviated mol.* One mole is the amount of matter that contains as many objects (atoms, molecules, or whatever other objects we are considering) as the number of atoms in exactly 12 g of isotopically pure ¹²C. From experiments, scientists have determined this number to be 6.0221421 × 10²³, which we will usually round to 6.02 × 10²³. Scientists call this valueAvogadro's number, N_A, in honor of the Italian scientist Amedeo Avogadro (1776–1856), and it is often cited with units of reciprocal moles, 6.02 × 10²³ mol⁻¹. The unit (read as either “inverse mole” or “per mole”) reminds us that there are 6.02 × 10²³ objects per one mole. A mole of atoms, a mole of molecules, or a mole of anything else all contain Avogadro's number of objects:

STRATEGIES IN CHEMISTRY
PROBLEM SOLVING

Practice is the key to success in solving problems. As you practice, you can improve your skills by following these steps:

Step 1: Analyze the problem. Read the problem carefully. What does it say? Draw a picture or diagram that will help you to visualize the problem. Write down both the data you are given and the quantity you need to obtain (the unknown).

Step 2: Develop a plan for solving the problem. Consider a possible path between the given information and the unknown. What principles or equations relate the known data to the unknown?

Recognize that some data may not be given explicitly in the problem; you may be expected to know certain quantities (such as Avogadro's number) or look them up in tables (such as atomic weights). Recognize also that your plan may involve either a single step or a series of steps with intermediate answers.

Step 3: Solve the problem. Use the known information and suitable equations or relationships to solve for the unknown. Dimensional analysis (Section 1.6) is a useful tool for solving a great number of problems. Be careful with significant figures, signs, and units.

Step 4: Check the solution. Read the problem again to make sure you have found all the solutions asked for in the problem. Does your answer make sense? That is, is the answer outrageously large or small or is it in the ballpark? Finally, are the units and significant figures correct?

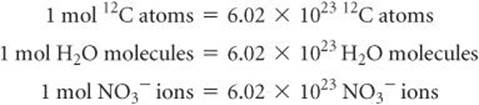
Avogadro's number is so large that it is difficult to imagine. Spreading 6.02 × 10²³ marbles over Earth's surface would produce a layer about 3 miles thick. Avogadro's number of pennies placed side by side in a straight line would encircle Earth 300 trillion (3 × 10¹⁴) times.

SAMPLE EXERCISE 3.7 Estimating Numbers of Atoms

Without using a calculator, arrange these samples in order of increasing numbers of carbon atoms: 12 g ¹²C, 1 mol C₂H₂, 9 × 10²³ molecules of CO₂.

SOLUTION

Analyze We are given amounts of three substances expressed in grams, moles, and number of molecules and asked to arrange the samples in order of increasing numbers of C atoms.

Plan To determine the number of C atoms in each sample, we must convert 12 g ¹²C, 1 mol C₂H₂, and 9 × 10²³ molecules CO₂ to numbers of C atoms. To make these conversions, we use the definition of mole and Avogadro's number.

Solve One mole is defined as the amount of matter that contains as many units of the matter as there are C atoms in exactly 12 g of ¹²C. Thus, 12 g of ¹²C contains 1 mol of C atoms = 6.02 × 10²³ C atoms. One mol of C₂H₂ contains 6 × 10²³ C₂H₂ molecules. Because there are two C atoms in each molecule, this sample contains 12 × 10²³ C atoms. Because each CO₂ molecule contains one C atom, the CO₂ sample contains 9 × 10²³ C atoms. Hence, the order is 12 g ¹²C (6 × 10²³ C atoms) 6 9 × 10²³ CO₂ molecules (9 × 10²³ C atoms) < 1 mol C₂H₂ (12 × 10²³ C atoms).

Check We can check our results by comparing numbers of moles of C atoms in the samples because the number of moles is proportional to the number of atoms. Thus, 12 g of ¹²C is 1 mol C; 1 mol of C₂H₂ contains 2 mol C, and 9 × 10²³ molecules of CO₂ contain 1.5 mol C, giving the same order as stated previously.

PRACTICE EXERCISE

Without using a calculator, arrange these samples in order of increasing number of O atoms: 1 mol H₂O, 1 mol CO₂, 3 × 10²³ molecules O₃.

Answer: 1 mol H₂O (6 × 10²³ O atoms) < 3 × 10²³ molecules O₃ (9 × 10²³ O atoms) < 1 mol CO₂ (12 × 10²³ O atoms)

SAMPLE EXERCISE 3.8 Converting Moles to Number of Atoms

Calculate the number of H atoms in 0.350 mol of C₆H₁₂O₆.

SOLUTION

Analyze We are given the amount of a substance (0.350 mol) and its chemical formula C₆H₁₂O₆. The unknown is the number of H atoms in the sample.

Plan Avogadro's number provides the conversion factor between number of moles of C₆H₁₂O₆ and number of molecules of C₆H₁₂O₆: 1 mol C₆H₁₂O₆ = 6.02 × 10²³ molecules C₆H₁₂O₆. Once we know the number of molecules of C₆H₁₂O₆, we can use the chemical formula, which tells us that each molecule of C₆H₁₂O₆ contains 12 H atoms. Thus, we convert moles of C₆H₁₂O₆ to molecules of C₆H₁₂O₆ and then determine the number of atoms of H from the number of molecules of C₆H₁₂O₆:

Moles C₆H₁₂O₆ → molecules C₆H₁₂O₆ → atoms H

Solve

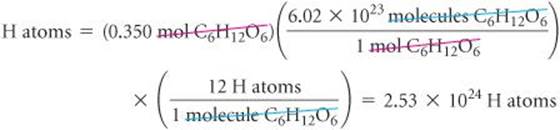
Check We can do a ballpark calculation: First, 0.35(6 × 10²³) is about 2 × 10²³ molecules of C₆H₁₂O₆, and each one of these molecules contains 12 H atoms. So 12(2 × 10²³) gives 24 × 10²³ = 2.4 × 10²⁴ H atoms, which agrees with our result. Because we were asked for the number of H atoms, the units of our answer are correct. The given data had three significant figures, so our answer has three significant figures.

PRACTICE EXERCISE

How many oxygen atoms are in (a) 0.25 mol Ca(NO₃)₂ and (b) 1.50 mol of sodium carbonate?

Answers: (a) 9.0 × 10²³, (b) 2.71 × 10²⁴

Molar Mass

A dozen is the same number, 12, whether we have a dozen eggs or a dozen elephants. Clearly, however, a dozen eggs does not have the same mass as a dozen elephants. Similarly, a mole is always the same number (6.02 × 10²³), but 1-mol samples of different substances have different masses. Compare, for example, 1 mol of ¹²C and 1 mol of ²⁴Mg. A single ¹²C atom has a mass of 12 amu, whereas a single ²⁴Mg atom is twice as massive, 24 amu (to two significant figures). Because a mole of anything always contains the same number of particles, a mole of ²⁴Mg must be twice as massive as a mole of ¹²C. Because a mole of ¹²C has a mass of 12 g (by definition), a mole of ²⁴Mg must have a mass of 24 g. This example illustrates a general rule relating the mass of an atom to the mass of Avogadro's number (1 mol) of these atoms: The atomic weight of an element in atomic mass units is numerically equal to the mass in grams of 1 mol of that element. For example,

Cl has an atomic weight of 35.5 amu 1 mol Cl has a mass of 35.5 g

Au has an atomic weight of 197 amu 1 mol Au has a mass of 197 g

For other kinds of substances, the same numerical relationship exists between formula weight and mass of one mole of a substance:

H₂O has a formula weight of 18.0 amu 1 mol H₂O has a mass of 18.0 g (FIGURE 3.9)

NO₃⁻ has a formula weight of 62.0 amu 1 mol NO₃⁻ has a mass of 62.0 g

NaCl has a formula weight of 58.5 amu 1 mol NaCl has a mass of 58.5 g

GO FIGURE

How many H₂O molecules are in a 9.00-g sample of water?

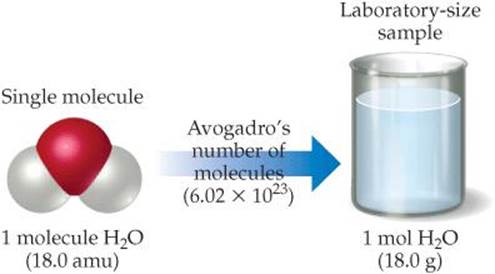
FIGURE 3.9 Comparing the mass of 1 molecule and 1 mol of H₂O. Both masses have the same number but different units (atomic mass units and grams). Expressing both masses in grams indicates their huge difference: 1 molecule H₂O has a mass of 2.99 × 10⁻²³ g whereas 1 mol H₂O has a mass of 18.0 g.

GIVE IT SOME THOUGHT

a. Which has more mass, a mole of water (H₂O) or a mole of glucose (C₆H₁₂O₆)?

b. Which contains more molecules, a mole of water or a mole of glucose?

The mass in grams of one mole of a substance (that is, the mass in grams per mole) is called the molar mass of the substance. The molar mass in grams per mole of any substance is numerically equal to its formula weight in atomic mass units. For NaCl, for example, the formula weight is 58.5 amu and the molar mass is 58.5 g/mol. Mole relationships for several other substances are shown in TABLE 3.2, and FIGURE 3.10 shows 1-mol quantities of three common substances.

The entries in Table 3.2 for N and N₂ point out the importance of stating the chemical form of a substance when using the mole concept. Suppose you read that 1 mol of nitrogen is produced in a particular reaction. You might interpret this statement to mean 1 mol of nitrogen atoms (14.0 g). Unless otherwise stated, however, what is probably meant is 1 mol of nitrogen molecules, N₂ (28.0 g), because N₂ is the most common chemical form of the element. To avoid ambiguity, it is important to state explicitly the chemical form being discussed. Using the chemical formula—N or N₂, for instance–– avoids ambiguity.

TABLE 3.2 • Mole Relationships

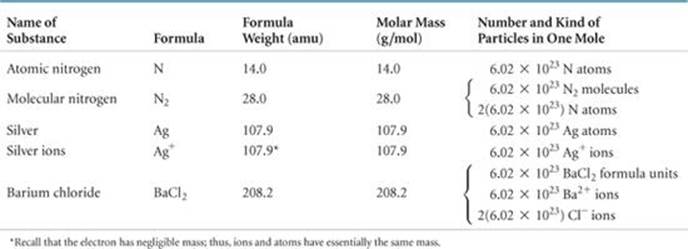
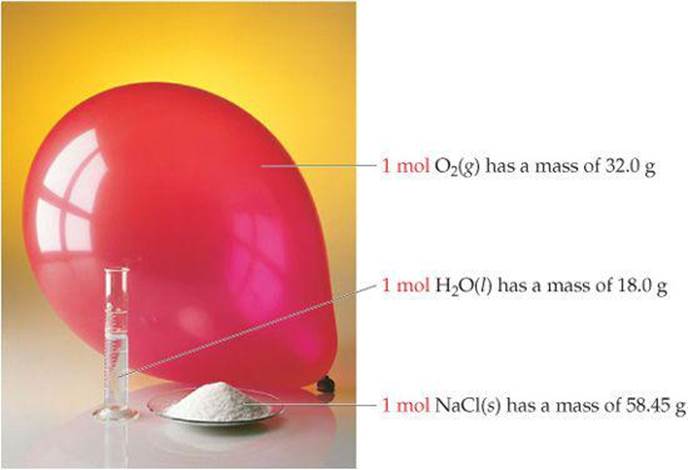
FIGURE 3.10 One mole each of a solid (NaCl), a liquid (H₂O), and a gas (O₂). In each case, the mass in grams of 1 mol––that is, the molar mass––is numerically equal to the formula weight in atomic mass units. Each of these samples contains 6.02 × 10²³ formula units.

SAMPLE EXERCISE 3.9 Calculating Molar Mass

What is the molar mass of glucose, C₆H₁₂O₆?

SOLUTION

Analyze We are given a chemical formula and asked to determine its molar mass.

Plan Because the molar mass of any substance is numerically equal to its formula weight, we first determine the formula weight of glucose by adding the atomic weights of its component atoms. The formula weight will have units of amu, whereas the molar mass has units of g/mol.

Solve Our first step is to determine the formula weight of glucose:

Because glucose has a formula weight of 180.0 amu, 1 mol of this substance (6.02 × 10²³ molecules) has a mass of 180.0 g. In other words, C₆H₁₂O₆ has a molar mass of 180.0 g/mol.

Check A magnitude below 250 seems reasonable based on the earlier examples we have encountered, and grams per mole is the appropriate unit for the molar mass.

Comment Glucose, also known as blood sugar, is found in nature in honey and fruits. Other sugars used as food are converted into glucose in the stomach or liver before the body uses them as energy sources. Because glucose requires no conversion, it is often given intravenously to patients who need immediate nourishment.

PRACTICE EXERCISE

Calculate the molar mass of Ca(NO₃)₂.

Answer: 164.1 g/mol

CHEMISTRY AND LIFE
GLUCOSE MONITORING

Over 20 million Americans have diabetes, and globally the number approaches 172 million. Diabetes is a metabolic disorder in which the body either cannot produce or cannot properly use the hormone insulin. One signal that a person is diabetic is that the concentration of glucose in the blood is higher than normal. Therefore, people who are diabetic need to measure their blood glucose concentrations regularly. Untreated diabetes can cause severe complications such as blindness and loss of limbs.

The body converts most of the food we eat into glucose. After digestion, glucose is delivered to cells via the blood. Cells need glucose to live, and insulin must be present in order for glucose to enter the cells. Normally, the body adjusts the concentration of insulin automatically, in concert with the glucose concentration after eating. However, in a diabetic person, either little or no insulin is produced (Type 1 diabetes) or insulin is produced but the cells cannot take it up properly (Type 2 diabetes). The result is that the blood glucose concentration is too high. People normally have a range of 70-120 mg glucose per deciliter of blood. A person who has not eaten for 8 hours or more is diagnosed as diabetic if his or her glucose level is 126 mg/dL or higher.

Glucose meters work by the introduction of blood from a person, usually by a prick of the finger, onto a small strip of paper that contains chemicals that react with glucose. Insertion of the strip into a small battery-operated reader gives the glucose concentration (FIGURE 3.11). The mechanism of the readout varies from one monitor to another—it may be a measurement of a small electrical current or measurement of light produced in a chemical reaction. Depending on the reading on any given day, a diabetic person may need to receive an injection of insulin or simply stop eating sweets for a while.

FIGURE 3.11 Glucose meter.

Interconverting Masses and Moles

Conversions of mass to moles and of moles to mass are frequently encountered in calculations using the mole concept. These calculations are simplified using dimensional analysis, as shown in Sample Exercises 3.10 and 3.11.

SAMPLE EXERCISE 3.10 Converting Grams to Moles

Calculate the number of moles of glucose (C₆H₁₂O₆) in 5.380 g of C₆H₁₂O₆.

SOLUTION

Analyze We are given the number of grams of a substance and its chemical formula and asked to calculate the number of moles.

Plan The molar mass of a substance provides the factor for converting grams to moles. The molar mass of C₆H₁₂O₆ is 180.0 g/mol (Sample Exercise 3.9).

Solve Using 1 mol C₆H₁₂O₆ = 180.0 g C₆H₁₂O₆ to write the appropriate conversion factor, we have

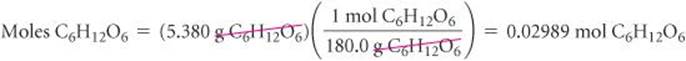
Check Because 5.380 g is less than the molar mass, an answer less than one mole is reasonable. The unit mol is appropriate. The original data had four significant figures, so our answer has four significant figures.

PRACTICE EXERCISE

How many moles of sodium bicarbonate (NaHCO₃) are in 508 g of NaHCO₃?

Answer: 6.05 mol NaHCO₃

SAMPLE EXERCISE 3.11 Converting Moles to Grams

Calculate the mass, in grams, of 0.433 mol of calcium nitrate.

SOLUTION

Analyze We are given the number of moles and the name of a substance and asked to calculate the number of grams in the sample.

Plan To convert moles to grams, we need the molar mass, which we can calculate using the chemical formula and atomic weights.

Solve Because the calcium ion is Ca²⁺ and the nitrate ion is NO₃⁻, calcium nitrate is Ca(NO₃)₂. Adding the atomic weights of the elements in the compound gives a formula weight of 164.1 amu. Using 1 mol Ca(NO₃)₂ = 164.1 g Ca(NO₃)₂ to write the appropriate conversion factor, we have

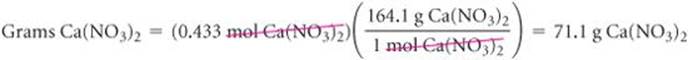
Check The number of moles is less than 1, so the number of grams must be less than the molar mass, 164.1 g. Using rounded numbers to estimate, we have 0.5 × 150 = 75 g, which means the magnitude of our answer is reasonable. Both the units (g) and the number of significant figures (3) are correct.

PRACTICE EXERCISE

What is the mass, in grams, of (a) 6.33 mol of NaHCO₃ and (b) 3.0 × 10⁻⁵ mol of sulfuric acid?

Answers: (a) 532 g, (b) 2.9 × 10⁻³ g

Interconverting Masses and Numbers of Particles

The mole concept provides the bridge between mass and number of particles. To illustrate how this bridge works, let's calculate the number of copper atoms in an old copper penny. Such a penny has a mass of about 3 g, and we assume it is 100% copper:

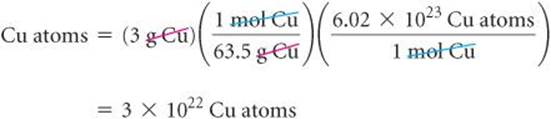
We have rounded our answer to one significant figure because we used only one significant figure for the mass of the penny. Notice how dimensional analysis (Section 1.6) provides a straightforward route from grams to numbers of atoms. The molar mass and Avogadro's number are used as conversion factors to convert grams to moles and then moles to atoms. Notice also that our answer is a very large number. Any time you calculate the number of atoms, molecules, or ions in an ordinary sample of matter, you can expect the answer to be very large. In contrast, the number of moles in a sample will usually be small, often less than 1.

The general procedure for interconverting mass and number of formula units (atoms, molecules, ions, or whatever else is represented by the chemical formula) is summarized in FIGURE 3.12.

GO FIGURE

What number would you use to convert (a) moles of CH₄ to grams of CH₄ and (b) number of molecules of CH₄ to moles of CH₄?

FIGURE 3.12 Procedure for interconverting mass and number of formula units. The number of moles of the substance is central to the calculation. Thus, the mole concept can be thought of as the bridge between the mass of a sample in grams and the number of formula units contained in the sample.

SAMPLE EXERCISE 3.12 Calculating Numbers of Molecules and Atoms from Mass

(a) How many glucose molecules are in 5.23 g of C₆H₁₂O₆? (b) How many oxygen atoms are in this sample?

SOLUTION

Analyze We are given the number of grams and the chemical formula and asked to calculate (a) the number of molecules and (b) the number of O atoms in the sample.

(a) Plan The strategy for determining the number of molecules in a given quantity of a substance is summarized in Figure 3.12. We must convert 5.23 g to moles of C₆H₁₂O₆ and then convert moles to molecules of C₆H₁₂O₆. The first conversion uses the molar mass of C₆H₁₂O₆, 180.0 g, and the second conversion uses Avogadro's number.

Solve Molecules C₆H₁₂O₆

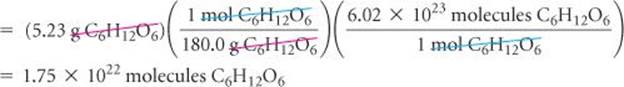
Check Because the mass we began with is less than a mole, there should be fewer than 6.02 × 10²³ molecules in the sample, which means the magnitude of our answer is reasonable. We can make a ballpark estimate of the answer: 5/200 = 2.5 × 10⁻² mol; 2.5 × 10⁻² × 6 × 10²³ = 15 × 10²¹ = 1.5 × 10²² molecules. The units (molecules) and significant figures (three) are appropriate.

(b) Plan To determine the number of O atoms, we use the fact that there are six O atoms in each C₆H₁₂O₆ molecule. Thus, multiplying the number of molecules we calculated in (a) by the factor (6 atoms O/1 molecule C₆H₁₂O₆) gives the number of O atoms.

Solve

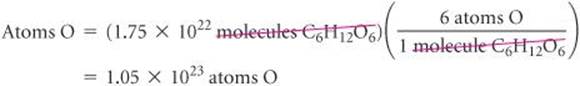
Check The answer is 6 times as large as the answer to part (a), exactly what it should be. The number of significant figures (three) and the units (atoms O) are correct.

PRACTICE EXERCISE

(a) How many nitric acid molecules are in 4.20 g of HNO₃? (b) How many O atoms are in this sample?

Answers: (a) 4.01 × 10²² molecules HNO₃, (b) 1.20 × 10²³ atoms O