CHEMISTRY THE CENTRAL SCIENCE
3 STOICHIOMETRY: CALCULATIONS WITH CHEMICAL FORMULAS AND EQUATIONS
3.5 EMPIRICAL FORMULAS FROM ANALYSES
As we learned in Section 2.6, the empirical formula for a substance tells us the relative number of atoms of each element in the substance. The empirical formula H2O shows that water contains two H atoms for each O atom. This ratio also applies on the molar level: 1 mol of H2O contains 2 mol of H atoms and 1 mol of O atoms. Conversely, the ratio of the numbers of moles of all elements in a compound gives the subscripts in the compound's empirical formula. Thus, the mole concept provides a way of calculating empirical formulas.
Mercury and chlorine, for example, combine to form a compound that is 73.9% mercury and 26.1% chlorine by mass. Thus, if we had a 100.0-g sample of the compound, it would contain 73.9 g of mercury and 26.1 g of chlorine. (Samples of any size can be used in problems of this type, but we will generally use 100.0 g to simplify the calculation of mass from percentage.) Using atomic weights to get molar masses, we can calculate the number of moles of each element in the sample:
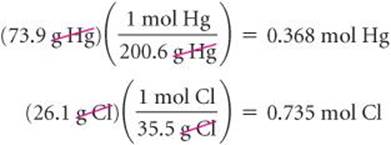
GO FIGURE
How do you calculate the mole ratio of each element in any compound?
FIGURE 3.13 Procedure for calculating an empirical formula from percentage composition. The key step in the calculation is step 2, determining the number of moles of each element in the compound.
We then divide the larger number of moles by the smaller number to obtain the Cl:Hg mole ratio:
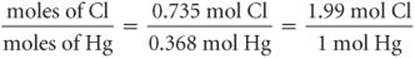
Because of experimental errors, calculated values for a mole ratio may not be whole numbers, as in the calculation here. The number 1.99 is very close to 2, however, and so we can confidently conclude that the empirical formula for the compound is HgCl2. The empirical formula is correct because its subscripts are the smallest integers that express the ratio of atoms present in the compound.
(Section 2.6).
The general procedure for determining empirical formulas is outlined in 
FIGURE 3.13.
GIVE IT SOME THOUGHT
What is the mole ratio of nitrogen to hydrogen in N2H4?
SAMPLE EXERCISE 3.13 Calculating an Empirical Formula
Ascorbic acid (vitamin C) contains 40.92% C, 4.58% H, and 54.50% O by mass. What is the empirical formula of ascorbic acid?
SOLUTION
Analyze We are to determine the empirical formula of a compound from the mass percentages of its elements.
Plan The strategy for determining the empirical formula involves the three steps given in Figure 3.13.
Solve
1. For simplicity, we assume we have exactly 100 g of material (although any other mass could also be used). In 100 g of ascorbic acid, we have
40.92 g C, 4.58 g H, and 54.50 g O.
2. We calculate the number of moles of each element:
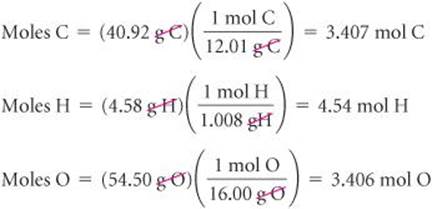
3. We determine the simplest whole-number ratio of moles by dividing each number of moles by the smallest number of moles:
The ratio for H is too far from 1 to attribute the difference to experimental error; in fact, it is quite close to 
. This suggests we should multiply the ratios by 3 to obtain whole numbers:
C:H:O = 3(1:1.33:1) = 3:4:3
Thus, the empirical formula is
C3H4O3
Check It is reassuring that the subscripts are moderate-size whole numbers. Also, calculating the percentage composition of C3H8O gives values very close to the original percentages.
PRACTICE EXERCISE
A 5.325-g sample of methyl benzoate, a compound used in the manufacture of perfumes, contains 3.758 g of carbon, 0.316 g of hydrogen, and 1.251 g of oxygen. What is the empirical formula of this substance?
Answer: C4H4O
Molecular Formulas from Empirical Formulas
We can obtain a molecular formula for any compound from its empirical formula if we know either the molecular weight or the molar mass of the compound. The subscripts in the molecular formula of a substance are always whole-number multiples of the subscripts in its empirical formula. (Section 2.6) This multiple can be found by dividing the molecular weight by the empirical formula weight:
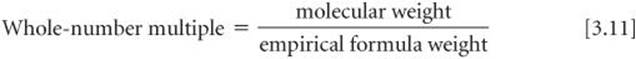
In Sample Exercise 3.13, for example, the empirical formula of ascorbic acid was determined to be C3H4O3. This means the empirical formula weight is 3(12.0 amu) + 4(1.0 amu) + 3(16.0 amu) = 88.0 amu. The experimentally determined molecular weight is 176 amu. Thus, we find the whole-number multiple that converts the empirical formula to the molecular formula by dividing:
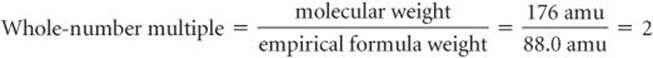
Consequently, we multiply the subscripts in the empirical formula by this multiple, giving the molecular formula: C6H8O6.
SAMPLE EXERCISE 3.14 Determining a Molecular Formula
Mesitylene, a hydrocarbon found in crude oil, has an empirical formula of C3H4 and an experimentally determined molecular weight of 121 amu. What is its molecular formula?
SOLUTION
Analyze We are given an empirical formula and a molecular weight and asked to determine a molecular formula.
Plan The subscripts in a compound's molecular formula are whole-number multiples of the subscripts in its empirical formula. We find the appropriate multiple by using Equation 3.11.
Solve The formula weight of the empirical formula C3H4 is
3(12.0 amu) + 4(1.0 amu) = 40.0 amu
Next, we use this value in Equation 3.11:
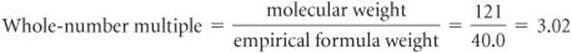
Only whole-number ratios make physical sense because molecules contain whole atoms. The 3.02 in this case could result from a small experimental error in the molecular weight. We therefore multiply each subscript in the empirical formula by 3 to give the molecular formula: C9H12.
Check We can have confidence in the result because dividing molecular weight by empirical formula weight yields nearly a whole number.
PRACTICE EXERCISE
Ethylene glycol, used in automobile antifreeze, is 38.7% C, 9.7% H, and 51.6% O by mass. Its molar mass is 62.1 g/mol. (a) What is the empirical formula of ethylene glycol? (b) What is its molecular formula?
Answers: (a) CH3O, (b) C2H6O2
Combustion Analysis
One technique for determining empirical formulas in the laboratory is combustion analysis, commonly used for compounds containing principally carbon and hydrogen.
When a compound containing carbon and hydrogen is completely combusted in an apparatus such as that shown in 
FIGURE 3.14, the carbon is converted to CO2 and the hydrogen is converted to H2O. (Section 3.2) The amounts of CO2 and H2O produced are determined by measuring the mass increase in the CO2 and H2O absorbers. From the masses of CO2 and H2O we can calculate the number of moles of C and H in the original sample and thereby the empirical formula. If a third element is present in the compound, its mass can be determined by subtracting the measured masses of C and H from the original sample mass.
FIGURE 3.14 Apparatus for combustion analysis.
SAMPLE EXERCISE 3.15 Determining an Empirical Formula by Combustion Analysis
Isopropyl alcohol, sold as rubbing alcohol, is composed of C, H, and O. Combustion of 0.255 g of isopropyl alcohol produces 0.561 g of CO2 and 0.306 g of H2O. Determine the empirical formula of isopropyl alcohol.
SOLUTION
Analyze We are told that isopropyl alcohol contains C, H, and O atoms and given the quantities of CO2 and H2O produced when a given quantity of the alcohol is combusted. We must determine the empirical formula for isopropyl alcohol, a task that requires us to calculate the number of moles of C, H, and O in the sample.
Plan We can use the mole concept to calculate grams of C in the CO2 and grams of H in the H2O. These masses are the masses of C and H in the alcohol before combustion. The mass of O in the compound equals the mass of the original sample minus the sum of the C and H masses. Once we have the C, H, and O masses, we can proceed as in Sample Exercise 3.13.
Solve
To calculate the mass of C from the measured mass of CO2, we first use the molar mass of CO2, 44.0 g/mol, to convert grams of CO2 to moles of CO2. Because each CO2 molecule has only one C atom, there is 1 mol of C atoms per mole of CO2 molecules. This fact allows us to convert moles of CO2 to moles of C. Finally, we use the molar mass of C, 12.0 g, to convert moles of C to grams of C:
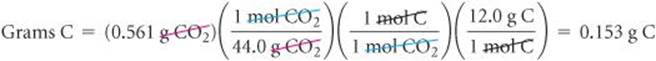
The calculation for determining H mass from H2O mass is similar, although we must remember that there are 2 mol of H atoms per 1 mol of H2O molecules:
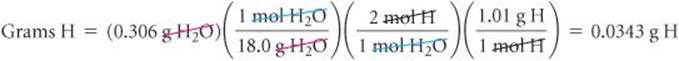
The mass of the sample, 0.255 g, is the sum of the masses of C, H, and O. Thus, the O mass is
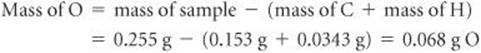
The number of moles of C, H, and O in the sample is therefore
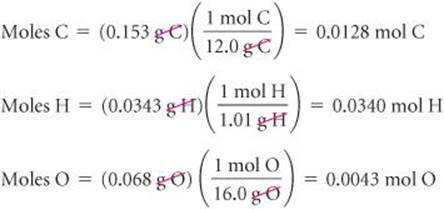
To find the empirical formula, we must compare the relative number of moles of each element in the sample. We determine relative number of moles by dividing each of our calculated number of moles by the smallest number:
The first two numbers are very close to the whole numbers 3 and 8, giving the empirical formula
C3H8O.
Check The subscripts work out to be moderate-size whole numbers, as expected.
PRACTICE EXERCISE
(a) Caproic acid, responsible for the odor of dirty socks, is composed of C, H, and O atoms. Combustion of a 0.225-g sample of this compound produces 0.512 g CO2 and 0.209 g H2O. What is the empirical formula of caproic acid? (b) Caproic acid has a molar mass of 116 g/mol. What is its molecular formula?
Answers: (a) C3H6O, (b) C6H12O2
GIVE IT SOME THOUGHT
In Sample Exercise 3.15, how do you explain the fact that the values in our calculated C:H:O ratio are 3.0:7.9:1.0 rather than exact integers 3:8:1?