CHEMISTRY THE CENTRAL SCIENCE

3 STOICHIOMETRY: CALCULATIONS WITH CHEMICAL FORMULAS AND EQUATIONS

3.6 QUANTITATIVE INFORMATION FROM BALANCED EQ UATIONS

The coefficients in a chemical equation represent the relative numbers of molecules in a reaction. The mole concept allows us to convert this information to the masses of the substances in the reaction. For instance, the coefficients in the balanced equation

indicate that two molecules of H₂ react with one molecule of O₂ to form two molecules of H₂O. It follows that the relative numbers of moles are identical to the relative numbers of molecules:

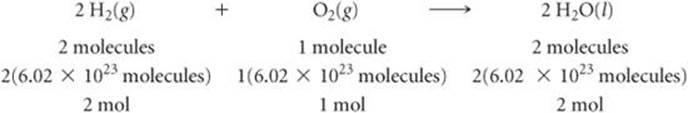
We can generalize this observation to all balanced chemical equations: The coefficients in a balanced chemical equation indicate both the relative numbers of molecules (or formula units) in the reaction and the relative numbers of moles. FIGURE 3.15 shows how this result corresponds to the law of conservation of mass.

The quantities 2 mol H₂, 1 mol O₂, and 2 mol H₂O given by the coefficients in Equation 3.12 are called stoichiometrically equivalent quantities. The relationship between these quantities can be represented as

where the symbol means “is stoichiometrically equivalent to.” Stoichiometric relations such as these can be used to convert between quantities of reactants and products in a chemical reaction. For example, the number of moles of H₂O produced from 1.57 mol of O₂ is

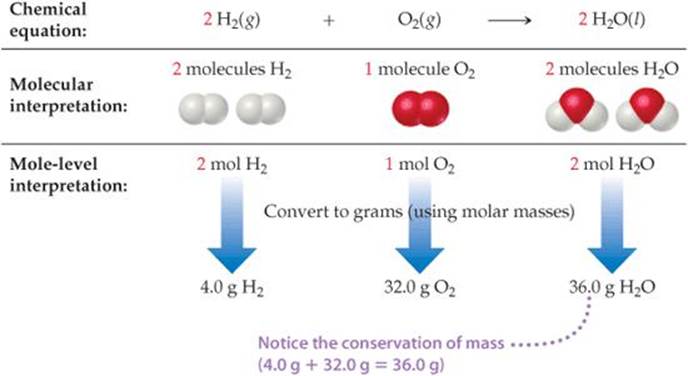
FIGURE 3.15 Interpreting a balanced chemical equation quantitatively.

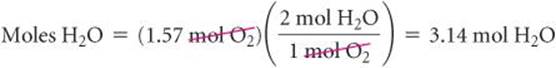
GIVE IT SOME THOUGHT

When 1.57 mol O₂ reacts with H₂ to form H₂O, how many moles of H₂ are consumed in the process?

As an additional example, consider the combustion of butane (C₄H₁₀), the fuel in disposable general-purpose lighters:

Let's calculate the mass of CO₂ produced when 1.00 g of C₄H₁₀ is burned. The coefficients in Equation 3.13 tell us how the amount of C₄H₁₀ consumed is related to the amount of CO₂ produced: 2 mol C₄H₁₀ 8 mol CO₂. To use this stoichiometric relationship, we must convert grams of C₄H₁₀ to moles using the molar mass of C₄H₁₀, 58.0 g/mol:

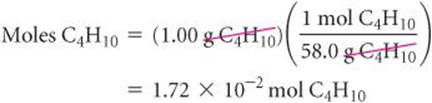
We then use the stoichiometric factor from the balanced equation to calculate moles of CO₂:

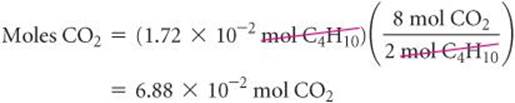
Finally, we use the molar mass of CO₂, 44.0 g/mol, to calculate the CO₂ mass in grams:

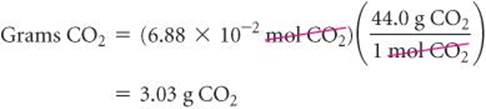
This conversion sequence involves three steps, as illustrated in FIGURE 3.16. These three conversions can be combined in a single equation:

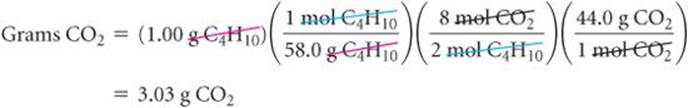
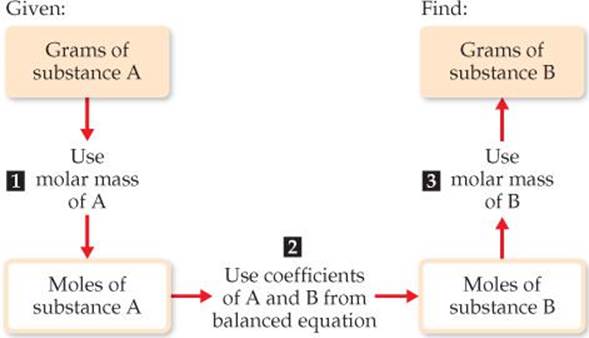
FIGURE 3.16 Procedure for calculating amounts of reactants consumed or products formed in a reaction. The number of grams of a reactant consumed or product formed can be calculated in three steps, starting with the number of grams of any reactant or product. Notice how molar masses and the coefficients in the balanced equation are used.

To calculate the amount of O₂ consumed in the reaction of Equation 3.13, we again rely on the coefficients in the balanced equation for our stoichiometric factor: 2 mol C₄H₁₀ 13 mol O₂:

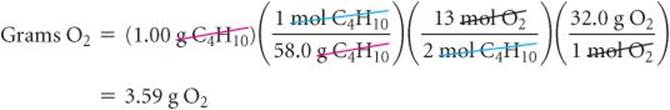
GIVE IT SOME THOUGHT

If 20.00 g of a compound reacts completely with 30.00 g of another compound in a combination reaction, how many grams of product are formed?

SAMPLE EXERCISE 3.16 Calculating Amounts of Reactants and Products

Determine how many grams of water are produced in the oxidation of 1.00 g of glucose, C₆H₁₂O₆:

C₆H₁₂O₆(s) + 6 O₂(g) → 6 CO₂(g) + 6 H₂O(l)

SOLUTION

Analyze We are given the mass of a reactant and must determine the mass of a product in the given reaction.

Plan The general strategy, as outlined in Figure 3.16, requires three steps:

1. Convert grams of C₆H₁₂O₆ to moles using the molar mass of C₆H₁₂O₆.

2. Convert moles of C₆H₁₂O₆ to moles of H₂O using the stoichiometric relationship 1 mol C₆H₁₂O₆ 6 mol H₂O.

3. Convert moles of H₂O to grams using the molar mass of H₂O.

Solve

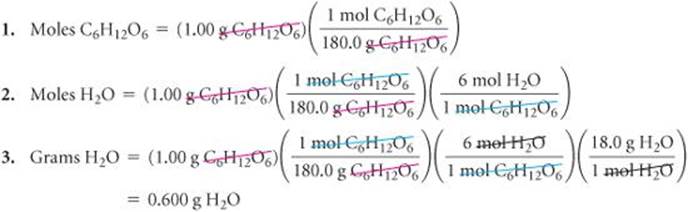
The steps can be summarized in a diagram like that in Figure 3.16:

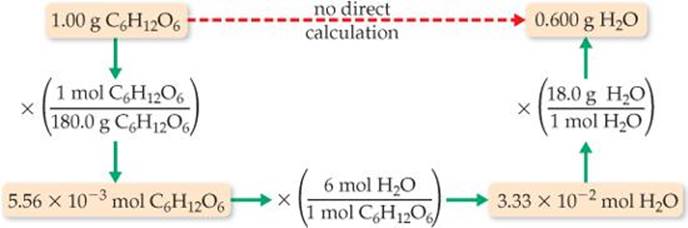
Check We can check how reasonable our result is by doing a ballpark estimate of the mass of H₂O. Because the molar mass of glucose is 180 g/mol, 1 gram of glucose equals 1/180 mol. Because one mole of glucose yields 6 mol H₂O, we would have 6/180 = 1/30 mol H₂O. The molar mass of water is 18 g/mol, so we have 1/30 × 18 = 6/10 = 0.6 g of H₂O, which agrees with the full calculation. The units, grams H₂O, are correct. The initial data had three significant figures, so three significant figures for the answer is correct.

Comment An average adult ingests 2 L of water daily and eliminates 2.4 L. The “extra” 0.4 L is produced in the metabolism of foodstuffs, such as oxidation of glucose. The desert rat (kangaroo rat), on the other hand, apparently never drinks water. It survives on its metabolic water.

PRACTICE EXERCISE

Decomposition of KClO₃ is sometimes used to prepare small amounts of O₂ in the laboratory: 2 KClO₃(s) → 2 KCl(s) + 3 O₂(g). How many grams of O₂ can be prepared from 4.50 g of KClO₃?

Answer: 1.77 g

SAMPLE EXERCISE 3.17 Calculating Amounts of Reactants and Products

Solid lithium hydroxide is used in space vehicles to remove the carbon dioxide gas exhaled by astronauts. The hydroxide reacts with the carbon dioxide to form solid lithium carbonate and liquid water. How many grams of carbon dioxide can be absorbed by 1.00 g of lithium hydroxide?

SOLUTION

Analyze We are given a verbal description of a reaction and asked to calculate the number of grams of one reactant that reacts with 1.00 g of another.

Plan The verbal description of the reaction can be used to write a balanced equation:

2 LiOH(s) + CO2(g) → Li₂CO₃(s) + H₂O(l)

We are given the mass in grams of LiOH and asked to calculate the mass in grams of CO₂. We can accomplish this task by using the three conversion steps in Figure 3.16. The conversion of step 1 requires the molar mass of LiOH (6.94 + 16.00 + 1.01 = 23.95 g/mol). The conversion of step 2 is based on a stoichiometric relationship from the balanced chemical equation: 2 mol LiOH 1 mol CO₂. For the step 3 conversion, we use the molar mass of CO₂: 12.01 + 2(16.00) = 44.01 g/mol.

Solve

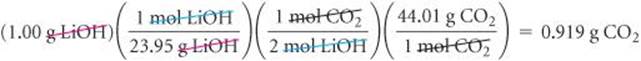
Check Notice that 23.95 g LiOH/mol ≈ 24 g LiOH/mol, that 24 g LiOH/mol × 2 mol LiOH = 48 g LiOH, and (44 g CO₂/mol)/(48 g LiOH) is slightly less than 1. Thus, the magnitude of our answer, 0.919 g CO₂, is reasonable based on the amount of starting LiOH. The significant figures and units are also appropriate.

PRACTICE EXERCISE

Propane, C₃H₈ (Figure 3.8), is a common fuel used for cooking and home heating. What mass of O₂ is consumed in the combustion of 1.00 g of propane?

Answer: 3.64 g