CHEMISTRY THE CENTRAL SCIENCE
5 THERMOCHEMISTRY

BIOENERGY. The sugars in sugarcane, produced from CO2, H2O, and sunshine via photosynthesis, can be converted into ethanol, which is used as an alternative to gasoline. In certain climates, such as that in Brazil, the sugarcane crop replenishes itself rapidly, making cane-based ethanol a sustainable fuel source.
WHAT'S AHEAD
5.1 THE NATURE OF ENERGY
We begin by considering the nature of energy and the forms it takes, notably kinetic energy and potential energy. We discuss the units used in measuring energy and the fact that energy can be used to do work or to transfer heat. To study energy changes, we focus on a particular part of the universe, which we call the system. Everything else is called the surroundings.
5.2 THE FIRST LAW OF THERMODYNAMICS
We then explore the first law of thermodynamics: Energy cannot be created or destroyed but can be transformed from one form to another or transferred between systems and surroundings. The energy possessed by a system is called its internal energy. Internal energy is a state function, a quantity whose value depends only on the current state of a system, not on how the system came to be in that state.
5.3 ENTHALPY
Next, we encounter a state function called enthalpy that is useful because the change in enthalpy measures the quantity of heat energy gained or lost by a system in a process occurring under constant pressure.
5.4 ENTHALPIES OF REACTION
We see that the enthalpy change associated with a chemical reaction is the enthalpies of the products minus the enthalpies of the reactants. This quantity is directly proportional to the amount of reactant consumed in the reaction.
5.5 CALORIMETRY
We next examine calorimetry, an experimental technique used to measure heat changes in chemical processes.
5.6 HESS'S LAW
We observe that the enthalpy change for a given reaction can be calculated using appropriate enthalpy changes for related reactions. To do so, we apply Hess's law.
5.7 ENTHALPIES OF FORMATION
Then we discuss how to establish standard values for enthalpy changes in chemical reactions and how to use them to calculate enthalpy changes for reactions.
5.8 FOODS AND FUELS
Finally, we examine foods and fuels as sources of energy and discuss some related health and social issues.
CHANCES ARE YOU'VE HEARD THE word energy today, perhaps in one of your courses, in the news, in conversation, or possibly in all these instances. Our modern society depends on energy for its existence. The issues surrounding energy—its sources, production, distribution, and consumption—pervade a lot of our conversation, from science to politics to economics to environmental issues. The production of energy is a major factor in the growth of national economies, especially rapidly developing countries such as China, India, and Brazil. The chapter-opening photograph highlights the efforts in Brazil to use their bountiful and fast-growing sugarcane crop as a source of ethanol. A major part of the Brazilian economy has depended on the use of ethanol instead of petroleum-based fuels in transportation and industry.
With the exception of the energy from the Sun, most of the energy used in our daily lives comes from chemical reactions. The combustion of gasoline, the production of electricity from coal, the heating of homes by natural gas, and the use of batteries to power electronic devices are all examples of how chemistry is used to produce energy. In addition, chemical reactions provide the energy that sustains living systems. Plants, such as the sugarcane in the chapter-opening photograph, use solar energy to carry out photosynthesis, allowing them to grow. The plants in turn provide food from which we humans derive the energy needed to move, maintain body temperature, and carry out all other bodily functions. What exactly is energy, though, and what principles are involved in its production, consumption, and transformation from one form to another?
In this chapter we begin to explore energy and its changes. We are motivated not only by the impact of energy on so many aspects of our daily lives but also by the fact that if we are to properly understand chemistry, we must understand the energy changes that accompany chemical reactions.
The study of energy and its transformations is known as thermodynamics (Greek: thérme, “heat”; dy'namis, “power”). This area of study began during the Industrial Revolution in order to develop the relationships among heat, work, and fuels in steam engines. In this chapter we will examine the relationships between chemical reactions and energy changes that involve heat. This portion of thermodynamics is called thermochemistry. We will discuss additional aspects of thermodynamics in Chapter 19.
![]() GO FIGURE
GO FIGURE
Why is a pitcher able to throw a baseball faster than he could throw a bowling ball?

![]() FIGURE 5.1 Work and heat, two forms of energy. (a) Work is energy used to cause an object to move. (b) Heat is energy used to cause the temperature of an object to increase.
FIGURE 5.1 Work and heat, two forms of energy. (a) Work is energy used to cause an object to move. (b) Heat is energy used to cause the temperature of an object to increase.
5.1 THE NATURE OF ENERGY
The concept of matter has always been easy to grasp because matter can be seen and touched. By contrast, although the concept of energy is a familiar one, it is challenging to deal with in a precise way. Energy is commonly defined as the capacity to do work or transfer heat. This definition requires us to understand the concepts of work and heat. Work is the energy used to cause an object to move against a force, and heat is the energy used to cause the temperature of an object to increase (![]() FIGURE 5.1). Let's begin our study of thermochemistry by examining the ways in which matter can possess energy and how that energy can be transferred from one piece of matter to another.
FIGURE 5.1). Let's begin our study of thermochemistry by examining the ways in which matter can possess energy and how that energy can be transferred from one piece of matter to another.
Kinetic Energy and Potential Energy
Objects, whether they are baseballs or molecules, can possess kinetic energy, the energy of motion. The magnitude of the kinetic energy, Ek, of an object depends on its mass, m, and speed, v:
![]()
We see that the kinetic energy of an object increases as its speed increases. For example, a car moving at 55 miles per hour (mph) has greater kinetic energy than it does at 25 mph. For a given speed the kinetic energy increases with increasing mass. Thus, a large truck traveling at 55 mph has greater kinetic energy than a small sedan traveling at the same speed because the truck has the greater mass. In chemistry, we are interested in the kinetic energy of atoms and molecules. Although too small to be seen, these particles have mass and are in motion and, therefore, possess kinetic energy.
All other kinds of energy—the energy stored in a stretched spring, in a weight held above your head, or in a chemical bond, for example—are potential energy. An object has potential energy by virtue of its position relative to other objects. Potential energy is, in essence, the “stored” energy that arises from the attractions and repulsions an object experiences in relation to other objects.
We are all familiar with instances in which potential energy is converted into kinetic energy. For example, think of a cyclist poised at the top of a hill (![]() FIGURE 5.2). Because of the attractive force of gravity, the potential energy of the cyclist and her bicycle is greater at the top of the hill than at the bottom. As a result, the bicycle easily moves down the hill with increasing speed. As it does so, the potential energy initially stored in it is converted into kinetic energy. The potential energy decreases as the bicycle rolls down the hill, but its kinetic energy increases as the speed increases (Equation 5.1).
FIGURE 5.2). Because of the attractive force of gravity, the potential energy of the cyclist and her bicycle is greater at the top of the hill than at the bottom. As a result, the bicycle easily moves down the hill with increasing speed. As it does so, the potential energy initially stored in it is converted into kinetic energy. The potential energy decreases as the bicycle rolls down the hill, but its kinetic energy increases as the speed increases (Equation 5.1).
We will soon see that this interconversion of energy, with one form decreasing while the other increases, is the first cornerstone of thermodynamics.
Gravitational forces play a negligible role in the ways that atoms and molecules interact with one another. Forces that arise from electrical charges are more important when dealing with atoms and molecules. One of the most important forms of potential energy in chemistry iselectrostatic potential energy, Eel, which arises from the interactions between charged particles. This energy is proportional to the electrical charges on the two interacting objects,Q1 andQ2, and inversely proportional to the distance, d, separating them:
![]() GO FIGURE
GO FIGURE
Suppose the bicyclist is coasting (not pedaling) at constant speed on a flat road and begins to go up a hill. If she does not start pedaling, what happens to her speed? Why?
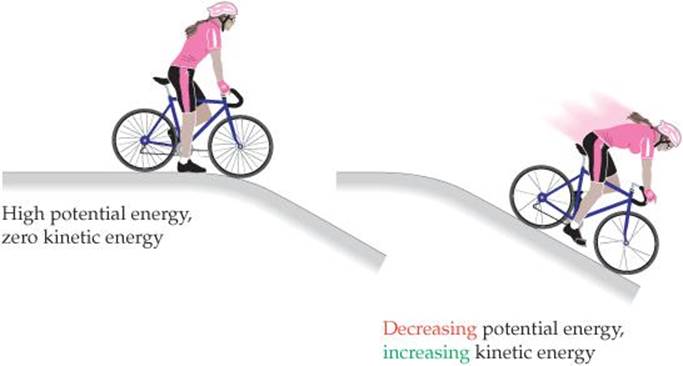
![]() FIGURE 5.2 Potential energy and kinetic energy. The potential energy initially stored in the motionless bicycle at the top of the hill is converted to kinetic energy as the bicycle moves down the hill and loses potential energy.
FIGURE 5.2 Potential energy and kinetic energy. The potential energy initially stored in the motionless bicycle at the top of the hill is converted to kinetic energy as the bicycle moves down the hill and loses potential energy.

Here k is simply a constant of proportionality, 8.99 × 109 J-m/C2. [C is the coulomb, a unit of electrical charge ![]() (Section 2.2), and J is the joule, a unit of energy we will discuss soon.] At the molecular level, the electrical chargesQ1 andQ2 are typically on the order of magnitude of the charge of the electron (1.60 × 10−19 C).
(Section 2.2), and J is the joule, a unit of energy we will discuss soon.] At the molecular level, the electrical chargesQ1 andQ2 are typically on the order of magnitude of the charge of the electron (1.60 × 10−19 C).
Equation 5.2 shows that the electrostatic potential energy goes to zero as d becomes infinite; in other words, the zero of electrostatic potential energy is defined as infinite separation of the charged particles. ![]() FIGURE 5.3 illustrates how Eel behaves for charges of the same and different sign. WhenQ1 andQ2 have the same sign (for example, both positive), the two charged particles repel each other, and a repulsive force pushes them apart. In this case, Eel is positive, and the potential energy decreases as the particles move farther and farther apart. WhenQ1 andQ2 have opposite signs, the particles attract each other, and an attractive force pulls them toward each other. In this case, Eel is negative, and the potential energy increases (becomes less negative) as the particles move apart.
FIGURE 5.3 illustrates how Eel behaves for charges of the same and different sign. WhenQ1 andQ2 have the same sign (for example, both positive), the two charged particles repel each other, and a repulsive force pushes them apart. In this case, Eel is positive, and the potential energy decreases as the particles move farther and farther apart. WhenQ1 andQ2 have opposite signs, the particles attract each other, and an attractive force pulls them toward each other. In this case, Eel is negative, and the potential energy increases (becomes less negative) as the particles move apart.
![]() GO FIGURE
GO FIGURE
A positively charged particle and a negatively charged particle are initially far apart. What happens to their electrostatic potential energy as they are brought closer together?
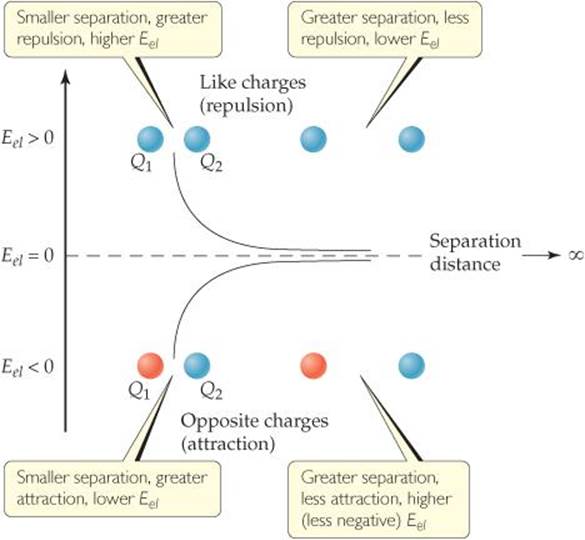
![]() FIGURE 5.3 Electrostatic potential energy. At finite separation distances for two charged particles, Eel is positive for like charges and negative for opposite charges. As the particles move farther apart, their electrostatic potential energy approaches zero.
FIGURE 5.3 Electrostatic potential energy. At finite separation distances for two charged particles, Eel is positive for like charges and negative for opposite charges. As the particles move farther apart, their electrostatic potential energy approaches zero.
These trends in electrostatic potential energy are used often in chemistry, as we will see later in the text.
One of our goals in chemistry is to relate the energy changes seen in the macroscopic world to the kinetic or potential energy of substances at the molecular level. Many substances—fuels, for example—release chemical energy when they react, energy due to the potential energy stored in the arrangements of their atoms. The energy a substance possesses because of its temperature (its thermal energy) is associated with the kinetic energy of the molecules in the substance.
![]() GIVE IT SOME THOUGHT
GIVE IT SOME THOUGHT
When the cyclist and bicycle in Figure 5.2 come to a stop at the bottom of the hill, (a) is the potential energy the same as it was at the top of the hill? (b) Is the kinetic energy the same as it was at the top of the hill?
Units of Energy
The SI unit for energy is the joule (pronounced “jool”), J, in honor of James Joule (1818–1889), a British scientist who investigated work and heat: 1 J = 1 kg-m2/s2. Equation 5.1 shows that a mass of 2 kg moving at a speed of 1 m/s possesses a kinetic energy of 1 J:
![]()
Because a joule is not a large amount of energy, we often use kilojoules (kJ) in discussing the energies associated with chemical reactions.
Traditionally, energy changes accompanying chemical reactions have been expressed in calories, a non-SI unit still widely used in chemistry, biology, and biochemistry. A calorie (cal) was originally defined as the amount of energy required to raise the temperature of 1 g of water from 14.5 °C to 15.5 °C. A calorie is now defined in terms of the joule:
1 cal = 4.184 J (exactly)
A related energy unit used in nutrition is the nutritional Calorie (note the capital C): 1 Cal = 1000 cal = 1 kcal.
System and Surroundings
When analyzing energy changes, we need to focus on a limited and well-defined part of the universe to keep track of the energy changes that occur. The portion we single out for study is called the system; everything else is called the surroundings. When we study the energy change that accompanies a chemical reaction in the laboratory, the re-actants and products constitute the system. The container and everything beyond it are considered the surroundings.
Systems may be open, closed, or isolated. An open system is one in which matter and energy can be exchanged with the surroundings. An uncovered pot of boiling water on a stove, such as in Figure 5.1(b), is an open system: Heat comes into the system from the stove, and water is released to the surroundings as steam.
The systems we can most readily study in thermochemistry are called closed systems—systems that can exchange energy but not matter with their surroundings. For example, consider a mixture of hydrogen gas, H2, and oxygen gas, O2, in a cylinder fitted with a piston (![]() FIGURE 5.4). The system is just the hydrogen and oxygen; the cylinder, piston, and everything beyond them (including us) are the surroundings. If the gases react to form water, energy is liberated:
FIGURE 5.4). The system is just the hydrogen and oxygen; the cylinder, piston, and everything beyond them (including us) are the surroundings. If the gases react to form water, energy is liberated:
![]() GO FIGURE
GO FIGURE
If the piston is pulled upward so that it sits halfway between the position shown and the top of the cylinder, is the system still closed?
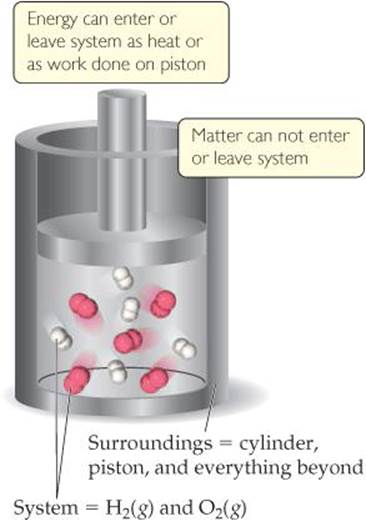
![]() FIGURE 5.4 A closed system.
FIGURE 5.4 A closed system.
![]()
Although the chemical form of the hydrogen and oxygen atoms in the system is changed by this reaction, the system has not lost or gained mass, which means it has not exchanged any matter with its surroundings. However, it can exchange energy with its surroundings in the form of workand heat.
An isolated system is one in which neither energy nor matter can be exchanged with the surroundings. An insulated thermos containing hot coffee approximates an isolated system. We know, however, that the coffee eventually cools, so it is not perfectly isolated.
![]() GIVE IT SOME THOUGHT
GIVE IT SOME THOUGHT
Is a human being an isolated, closed, or open system?
Transferring Energy: Work and Heat
Figure 5.1 illustrates the two ways we experience energy changes in our everyday lives—in the form of work and in the form of heat. In Figure 5.1(a) work is done as energy is transferred from the pitcher's arm to the ball, directing it toward the plate at high speed. In Figure 5.1(b) energy is transferred in the form of heat. Causing the motion of an object against a force and causing a temperature change are the two general ways that energy can be transferred into or out of a system.
A force is any push or pull exerted on an object. We define work, w, as the energy transferred when a force moves an object. The magnitude of this work equals the product of the force, F, and the distance, d, the object moves:
![]()
We perform work, for example, when we lift an object against the force of gravity. If we define the object as the system, then we—as part of the surroundings—are performing work on that system, transferring energy to it.
The other way in which energy is transferred is as heat. Heat is the energy transferred from a hotter object to a colder one. A combustion reaction, such as the burning of natural gas illustrated in Figure 5.1(b), releases the chemical energy stored in the molecules of the fuel. ![]() (Section 3.2) If we define the substances involved in the reaction as the system and everything else as the surroundings, we find that the released energy causes the temperature of the system to increase. Energy in the form of heat is then transferred from the hotter system to the cooler surroundings.
(Section 3.2) If we define the substances involved in the reaction as the system and everything else as the surroundings, we find that the released energy causes the temperature of the system to increase. Energy in the form of heat is then transferred from the hotter system to the cooler surroundings.
SAMPLE EXERCISE 5.1 Describing and Calculating Energy Changes
A bowler lifts a 5.4-kg (12-lb) bowling ball from ground level to a height of 1.6 m (5.2 ft) and then drops it. (a) What happens to the potential energy of the ball as it is raised? (b) What quantity of work, in J, is used to raise the ball? (c) After the ball is dropped, it gains kinetic energy. If all the work done in part (b) has been converted to kinetic energy by the time the ball strikes the ground, what is the ball's speed just before it hits the ground? (Note: The force due to gravity is F = m × g, where m is the mass of the object and g is the gravitational constant; g = 9.8 m/s2.)
SOLUTION
Analyze We need to relate the potential energy of the bowling ball to its position relative to the ground. We then need to establish the relationship between work and the change in the ball's potential energy. Finally, we need to connect the change in potential energy when the ball is dropped with the kinetic energy attained by the ball.
Plan We can calculate the work done in lifting the ball by using Equation 5.3: w = F × d. The kinetic energy of the ball just before it hits the ground equals its initial potential energy. We can use the kinetic energy and Equation 5.1 to calculate the speed, v, just before impact.
Solve
(a) Because the ball is raised above the ground, its potential energy relative to the ground increases.
(b) The ball has a mass of 5.4 kg and is lifted 1.6 m. To calculate the work performed to raise the ball, we use Equation 5.3 and F = m × g for the force that is due to gravity:
w = F × d = m × g × d = (5.4 kg)(9.8 m/s2)(1.6 m) = 85 kg-m2s2 = 85 J
Thus, the bowler has done 85 J of work to lift the ball to a height of 1.6 m.
(c) When the ball is dropped, its potential energy is converted to kinetic energy. We assume that the kinetic energy just before the ball hits the ground is equal to the work done in part (b), 85 J:
![]()
We can now solve this equation for v:

Check Work must be done in (b) to increase the potential energy of the ball, which is in accord with our experience. The units are appropriate in (b) and (c). The work is in units of J and the speed in units of m/s. In (c) we carry an additional digit in the intermediate calculation involving the square root, but we report the final value to only two significant figures, as appropriate.
Comment A speed of 1 m/s is roughly 2 mph, so the bowling ball has a speed greater than 10 mph just before impact.
PRACTICE EXERCISE
What is the kinetic energy, in J, of (a) an Ar atom moving at a speed of 650 m/s, (b) a mole of Ar atoms moving at 650 m/s? (Hint: 1 amu = 1.66 × 10−27 kg.)
Answers: (a) 1.4 × 10−20 J, (b) 8.4 × 103 J