CHEMISTRY THE CENTRAL SCIENCE
5 THERMOCHEMISTRY
5.2 THE FIRST LAW OF THERMODYNAMICS
We have seen that the potential energy of a system can be converted into kinetic energy, and vice versa. We have also seen that energy can be transferred back and forth between a system and its surroundings in the forms of work and heat. All of these conversions and transfers proceed in accord with one of the most important observations in science: Energy can be neither created nor destroyed. Any energy that is lost by a system must be gained by the surroundings, and vice versa. This important observation—that energy is conserved—is known as the first law of thermodynamics. To apply this law quantitatively, let's first define the energy of a system more precisely.
Internal Energy
We will use the first law of thermodynamics to analyze energy changes in chemical systems. In order to do so, we must consider all the sources of kinetic and potential energy in the system we are studying. We define the internal energy, E, of a system as the sum of all the kinetic and potential energies of the components of the system. For the system in Figure 5.4, for example, the internal energy includes not only the motions and interactions of the H2 and O2 molecules but also the motions and interactions of the nuclei and electrons. We generally do not know the numerical value of a system's internal energy. In thermodynamics, we are mainly concerned with the change in E (and, as we shall see, changes in other quantities as well) that accompanies a change in the system.
Imagine that we start with a system with an initial internal energy E initial. The system then undergoes a change, which might involve work being done or heat being transferred. After the change, the final internal energy of the system is Efinal. We define the change in internal energy, denoted ΔE (read “delta E”),* as the difference between Efinal and Einitial:
![]()
We generally can't determine the actual values of Efinal and Einitial for any system of practical interest. Nevertheless, one of the beautiful aspects of the first law of thermodynamics is that we need only the value of ΔE in order to apply the law. We can often determine the value of ΔE even though we don't know the specific values of Efinal and Einitial.
Thermodynamic quantities such as ΔE have three parts: (1) a number and (2) a unit, which together give the magnitude of the change, and (3) a sign that gives the direction. A positive value of ΔE results when Efinal> E initial, indicating that the system has gained energy from its surroundings. A negative value of ΔE results when Efinal< Einitial, indicating that the system has lost energy to its surroundings. Notice that we are taking the point of view of the system rather than that of the surroundings in discussing the energy changes. We need to remember, however, that any increase in the energy of the system is accompanied by a decrease in the energy of the surroundings, and vice versa. These features of energy changes are summarized in ![]() FIGURE 5.5.
FIGURE 5.5.
![]() GO FIGURE
GO FIGURE
What is the value of ΔE if Efinal equals Einitial?
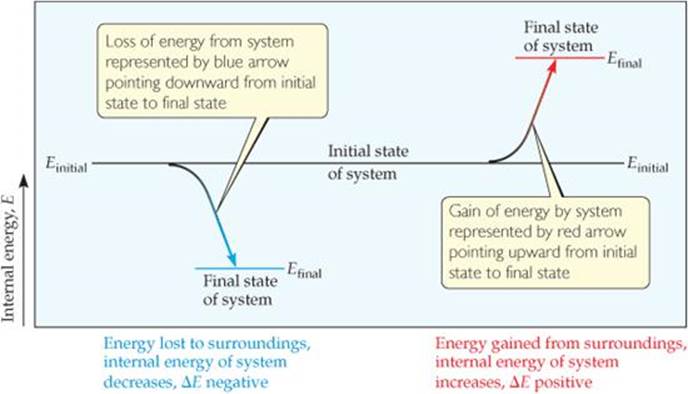
![]() FIGURE 5.5 Changes in internal energy.
FIGURE 5.5 Changes in internal energy.
In a chemical reaction, the initial state of the system refers to the reactants and the final state refers to the products. In the reaction
2 H2(g) + O2(g) → 2 H2O(l)
for instance, the initial state is the 2 H2(g) + O2(g) and the final state is the 2 H2O(l). When hydrogen and oxygen form water at a given temperature, the system loses energy to the surroundings. Because energy is lost from the system, the internal energy of the products (final state) is less than that of the reactants (initial state), and ΔE for the process is negative. Thus, the energy diagram in ![]() FIGURE 5.6 shows that the internal energy of the mixture of H2 and O2 is greater than that of the H2O produced in the reaction.
FIGURE 5.6 shows that the internal energy of the mixture of H2 and O2 is greater than that of the H2O produced in the reaction.
![]() GO FIGURE
GO FIGURE
The internal energy for Mg(s) and Cl2(g) is greater than that of MgCl2(s). Sketch an energy diagram that represents the reaction MgCl2(s) → Mg(s) + Cl2(g).
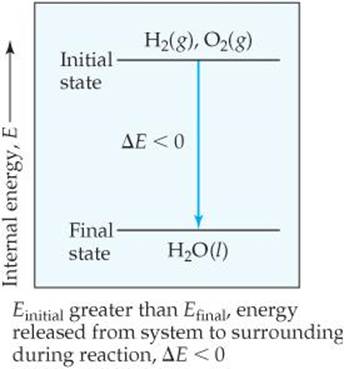
![]() FIGURE 5.6 Energy diagram for the reaction 2 H2(g) + O2(g) → 2 H2O(I).
FIGURE 5.6 Energy diagram for the reaction 2 H2(g) + O2(g) → 2 H2O(I).
Relating ΔE to Heat and Work
As we noted in Section 5.1, a system may exchange energy with its surroundings in two general ways: as heat or as work. The internal energy of a system changes in magnitude as heat is added to or removed from the system or as work is done on or by the system. If we think of internal energy as the system's bank account of energy, we see that deposits or withdrawals can be made either in increments of heat or in increments of work. Deposits increase the energy of the system (positive ΔE), whereas withdrawals decrease the energy of the system (negative ΔE).
![]() GO FIGURE
GO FIGURE
Suppose a system receives a “deposit” of work from the surroundings and loses a “withdrawal” of heat to the surroundings. Can we determine the sign of ΔE for this process?

![]() FIGURE 5.7 Sign conventions for heat and work. Heat, q, gained by a system and work, w, done on a system are both positive quantities, corresponding to “deposits” of internal energy into the system. Conversely, heat transferred from the system to the surroundings and work done by the system on the surroundings are both “withdrawals” of internal energy from the system.
FIGURE 5.7 Sign conventions for heat and work. Heat, q, gained by a system and work, w, done on a system are both positive quantities, corresponding to “deposits” of internal energy into the system. Conversely, heat transferred from the system to the surroundings and work done by the system on the surroundings are both “withdrawals” of internal energy from the system.
We can use these ideas to write a useful algebraic expression of the first law of thermodynamics. When a system undergoes any chemical or physical change, the accompanying change in internal energy ΔE, is the sum of the heat added to or liberated from the system, q, and the work done on or by the system, w:
![]()
When heat is added to a system or work is done on a system, its internal energy increases. Therefore, when heat is transferred to the system from the surroundings, q has a positive value. Adding heat to the system is like making a deposit to the energy account—the energy of the system increases (![]() FIGURE 5.7). Likewise, when work is done on the system by the surroundings, w has a positive value. Conversely, both the heat lost by the system to the surroundings and the work done by the system on the surroundings have negative values; that is, they lower the internal energy of the system. They are energy withdrawals and lower the amount of energy in the system's account.
FIGURE 5.7). Likewise, when work is done on the system by the surroundings, w has a positive value. Conversely, both the heat lost by the system to the surroundings and the work done by the system on the surroundings have negative values; that is, they lower the internal energy of the system. They are energy withdrawals and lower the amount of energy in the system's account.
The sign conventions for q, w, and ΔE are summarized in ![]() TABLE 5.1. Notice that any energy entering the system as either heat or work carries a positive sign.
TABLE 5.1. Notice that any energy entering the system as either heat or work carries a positive sign.
TABLE 5.1 • Sign Convention for q, w and ΔE

SAMPLE EXERCISE 5.2 Relating Heat and Work to Changes of Internal Energy
Gases A(g) and B(g) are confined in a cylinder-and-piston arrangement like that in Figure 5.4 and react to form a solid product C(s): A(g) + B(g) → C(s). As the reaction occurs, the system loses 1150 J of heat to the surroundings. The piston moves downward as the gases react to form a solid. As the volume of the gas decreases under the constant pressure of the atmosphere, the surroundings do 480 J of work on the system. What is the change in the internal energy of the system?
SOLUTION
Analyze The question asks us to determine ΔE, given information about q and w.
Plan We first determine the signs of q and w (Table 5.1) and then use Equation 5.5, ΔE = q + w, to calculate ΔE.
Solve Heat is transferred from the system to the surroundings, and work is done on the system by the surroundings, so q is negative and w is positive: q = –1150 J and w = 480 kJ. Thus,
ΔE = q + w = (–1150 J) + (480 J) = – 670 J
The negative value of ΔE tells us that a net quantity of 670 J of energy has been transferred from the system to the surroundings.
Comment You can think of this change as a decrease of 670 J in the net value of the system's energy bank account (hence, the negative sign); 1150 J is withdrawn in the form of heat while 480 J is deposited in the form of work. Notice that as the volume of the gases decreases, work is being done on the system by the surroundings, resulting in a deposit of energy.
PRACTICE EXERCISE
Calculate the change in the internal energy for a process in which a system absorbs 140 J of heat from the surroundings and does 85 J of work on the surroundings.
Answer: +55 J
Endothermic and Exothermic Processes
Because transfer of heat to and from the system is central to our discussion in this chapter, we have some special terminology to indicate the direction of transfer. When a process occurs in which the system absorbs heat, the process is called endothermic (endo- means “into”). During an endothermic process, such as the melting of ice, heat flows into the system from its surroundings [![]() FIGURE 5.8 (a)]. If we, as part of the surroundings, touch a container in which ice is melting, the container feels cold to us because heat has passed from our hand to the container.
FIGURE 5.8 (a)]. If we, as part of the surroundings, touch a container in which ice is melting, the container feels cold to us because heat has passed from our hand to the container.
A process in which the system loses heat is called exothermic (exo- means “out of”). During an exothermic process, such as the combustion of gasoline, heat exits or flows out of the system into the surroundings [Figure 5.8(b)].
![]() GIVE IT SOME THOUGHT
GIVE IT SOME THOUGHT
When H2(g) and O2(g) react to form H2O(l), heat is released to the surroundings. Consider the reverse reaction, namely, the formation of H2(g) and O2(g) from H2O(l): 2 H2O(l) → 2 H2(g) + O2(g). Is this reaction exothermic or endothermic? (Hint: Refer to Figure 5.6)
State Functions
Although we usually have no way of knowing the precise value of the internal energy of a system, E, it does have a fixed value for a given set of conditions. The conditions that influence internal energy include the temperature and pressure. Furthermore, the internal energy of a system is proportional to the total quantity of matter in the system because energy is an extensive property. ![]() (Section 1.3)
(Section 1.3)
Suppose we define our system as 50 g of water at 25 °C (![]() FIGURE 5.9). The system could have reached this state by cooling 50 g of water from 100 °C to 25 °C or by melting 50 g of ice and subsequently warming the water to 25 °C. The internal energy of the water at 25 °C is the same in either case. Internal energy is an example of a state function, a property of a system that is determined by specifying the system's condition, or state (in terms of temperature, pressure, and so forth). The value of a state function depends only on the present state of the system, not on the path the system took to reach that state. Because E is a state function, ΔE depends only on the initial and final states of the system, not on how the change occurs.
FIGURE 5.9). The system could have reached this state by cooling 50 g of water from 100 °C to 25 °C or by melting 50 g of ice and subsequently warming the water to 25 °C. The internal energy of the water at 25 °C is the same in either case. Internal energy is an example of a state function, a property of a system that is determined by specifying the system's condition, or state (in terms of temperature, pressure, and so forth). The value of a state function depends only on the present state of the system, not on the path the system took to reach that state. Because E is a state function, ΔE depends only on the initial and final states of the system, not on how the change occurs.

![]() FIGURE 5.8 Endothermic and exothermic reactions. (a) When ammonium thiocyanate and barium hydroxide octahydrate are mixed at room temperature, the temperature drops. (b) The reaction of powdered aluminum with Fe2O3 (the thermite reaction) proceeds vigorously, releasing heat and forming Al2O3 and molten iron.
FIGURE 5.8 Endothermic and exothermic reactions. (a) When ammonium thiocyanate and barium hydroxide octahydrate are mixed at room temperature, the temperature drops. (b) The reaction of powdered aluminum with Fe2O3 (the thermite reaction) proceeds vigorously, releasing heat and forming Al2O3 and molten iron.
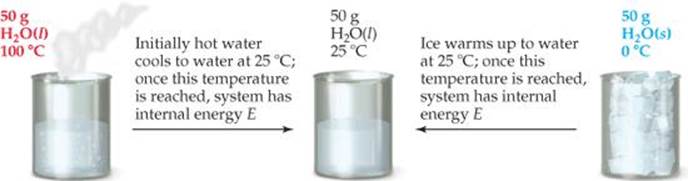
![]() FIGURE 5.9 Internal energy, E, a state function. Any state function depends only on the present state of the system and not on the path by which the system arrived at that state.
FIGURE 5.9 Internal energy, E, a state function. Any state function depends only on the present state of the system and not on the path by which the system arrived at that state.
An analogy may help you understand the difference between quantities that are state functions and those that are not. Suppose you drive from Chicago, which is 596 ft above sea level, to Denver, which is 5280 ft above sea level. No matter which route you take, the altitude change is 4684 ft. The distance you travel, however, depends on your route. Altitude is analogous to a state function because the change in altitude is independent of the path taken. Distance traveled is not a state function.
Some thermodynamic quantities, such as E, are state functions. Other quantities, such as q and w, are not. This means that, although ΔE = q + w does not depend on how the change occurs, the specific amounts of heat and work produced depend on the way in which the change occurs, analogous to the choice of travel route between Chicago and Denver. Nevertheless, if changing the path by which a system goes from an initial state to a final state increases the value of q, that path change will also decrease the value of w by exactly the same amount. The result is that ΔE is the same for the two paths.
We can illustrate this principle using a flashlight battery as our system. As the battery is discharged, its internal energy decreases as the energy stored in the battery is released to the surroundings. In ![]() FIGURE 5.10, we consider two possible ways of discharging the battery at constant temperature. If a wire shorts out the battery, no work is accomplished because nothing is moved against a force. All the energy lost from the battery is in the form of heat. (The wire gets warmer and releases heat to the surroundings.) If the battery is used to make a motor turn, the discharge produces work. Some heat is released, but not as much as when the battery is shorted out. We see that the magnitudes of q and w must be different for these two cases. If the initial and final states of the battery are identical in the two cases, however, then ΔE = q + w must be the same in both cases because ΔE is a state function. Remember: ΔE depends only on the initial and final states of the system, not on the specific path taken from the initial to the final state.
FIGURE 5.10, we consider two possible ways of discharging the battery at constant temperature. If a wire shorts out the battery, no work is accomplished because nothing is moved against a force. All the energy lost from the battery is in the form of heat. (The wire gets warmer and releases heat to the surroundings.) If the battery is used to make a motor turn, the discharge produces work. Some heat is released, but not as much as when the battery is shorted out. We see that the magnitudes of q and w must be different for these two cases. If the initial and final states of the battery are identical in the two cases, however, then ΔE = q + w must be the same in both cases because ΔE is a state function. Remember: ΔE depends only on the initial and final states of the system, not on the specific path taken from the initial to the final state.
![]() GIVE IT SOME THOUGHT
GIVE IT SOME THOUGHT
In what ways is the balance in your checkbook a state function?
![]() GO FIGURE
GO FIGURE
If the battery is defined as the system, what is the sign on w in part (b)?
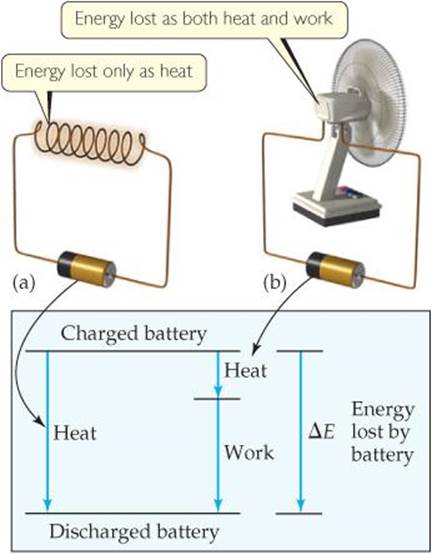
![]() FIGURE 5.10 Internal energy is a state function, but heat and work are not. (a) A battery shorted out by a wire loses energy to the surroundings only as heat; no work is performed. (b) A battery discharged through a motor loses energy as work (to make the fan turn) and also loses some energy as heat. The value of ΔE is the same for both processes even though the values of q and w in (a) are different from those in (b).
FIGURE 5.10 Internal energy is a state function, but heat and work are not. (a) A battery shorted out by a wire loses energy to the surroundings only as heat; no work is performed. (b) A battery discharged through a motor loses energy as work (to make the fan turn) and also loses some energy as heat. The value of ΔE is the same for both processes even though the values of q and w in (a) are different from those in (b).