CHEMISTRY THE CENTRAL SCIENCE
1 INTRODUCTION: MATTER AND MEASUREMENT
1.4 UNITS OF MEASUREMENT
Many properties of matter are quantitative, that is, associated with numbers. When a number represents a measured quantity, the units of that quantity must be specified. To say that the length of a pencil is 17.5 is meaningless. Expressing the number with its units, 17.5 centimeters (cm), properly specifies the length. The units used for scientific measurements are those of the metric system.
The metric system, developed in France during the late eighteenth century, is used as the system of measurement in most countries. The United States has traditionally used the English system, although use of the metric system has become more common (![]() FIGURE 1.15).
FIGURE 1.15).

![]() FIGURE 1.15 Metric units. Metric measurements are increasingly common in the United States, as exemplified by the volume printed on this soda can in both English units (fluid ounces, fl oz) and metric units (milliliters, mL).
FIGURE 1.15 Metric units. Metric measurements are increasingly common in the United States, as exemplified by the volume printed on this soda can in both English units (fluid ounces, fl oz) and metric units (milliliters, mL).
 A CLOSER LOOK
A CLOSER LOOK
THE SCIENTIFIC METHOD
Although two scientists rarely approach the same problem in exactly the same way, they use guidelines for the practice of science known as the scientific method. As ![]() FIGURE 1.16 shows, we begin by collecting information, or data, by observation and experiment. The ultimate goal, however, is not collecting data but rather finding a pattern or sense of order in our observations and understanding the origin of this order.
FIGURE 1.16 shows, we begin by collecting information, or data, by observation and experiment. The ultimate goal, however, is not collecting data but rather finding a pattern or sense of order in our observations and understanding the origin of this order.
As we gather more data, we may see patterns that lead us to a tentative explanation, or hypothesis, that guides us in planning further experiments. A key feature of a good hypothesis is that it proposes a mechanism that underlies our observations and can be used to make predictions about new experiments. If a hypothesis is sufficiently general and repeatedly effective in predicting results of future experiments, it is called a theory. A theory is an explanation of the general causes of certain phenomena, with considerable evidence or facts to support it. For example, Einstein's theory of relativity was a revolutionary way of thinking about space and time. It was more than just a hypothesis because it could be used to make predictions that could be tested experimentally. The results of these experiments were generally in agreement with Einstein's predictions and were not explainable by earlier theories.
In spite of the landmark achievements of Einstein's theory, scientists can never say the theory is “proven.” A theory that has excellent predictive power today may not work as well in the future as more data and improved scientific equipment are developed. Thus, science is always a work in progress.
Eventually, we may be able to tie together a great number of observations in a scientific law, which is a concise verbal statement or mathematical equation that summarizes a broad variety of observations and experiences. We tend to think of scientific laws as the basic rules under which nature operates. However, it is not so much that matter obeys these laws, but rather that these laws describe the behavior of matter. As we proceed through this text, we will rarely have the opportunity to discuss the doubts, conflicts, clashes of personalities, and revolutions of perception that have led to our present scientific ideas. You need to be aware that just because we can spell out the results of science so concisely and neatly in textbooks does not mean scientific progress is smooth, certain, and predictable. Some of the ideas we present in this text took centuries to develop and involved many scientists. We gain our view of the natural world by standing on the shoulders of the scientists who came before us. Take advantage of this view. As you study, exercise your imagination. Don't be afraid to ask daring questions when they occur to you. You may be fascinated by what you discover!
RELATED EXERCISE: 1.58
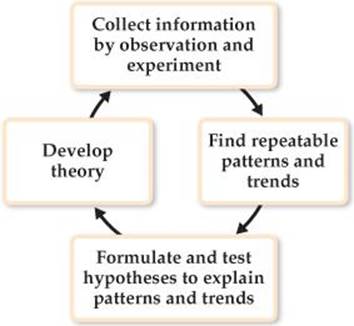
![]() FIGURE 1.16 The scientific method. This general approach to solving problems involves making observations, confirming that they are reproducible, seeking patterns in the observations, formulating hypotheses to explain the observations, and testing these hypotheses by further experiments. Hypotheses that withstand such tests and prove themselves useful in explaining and predicting behavior become known as theories.
FIGURE 1.16 The scientific method. This general approach to solving problems involves making observations, confirming that they are reproducible, seeking patterns in the observations, formulating hypotheses to explain the observations, and testing these hypotheses by further experiments. Hypotheses that withstand such tests and prove themselves useful in explaining and predicting behavior become known as theories.
SI Units
In 1960 an international agreement was reached specifying a particular choice of metric units for use in scientific measurements. These preferred units are called SI units, after the French Système International d'Unités. This system has seven base units from which all other units are derived (![]() TABLE 1.4). In this chapter we will consider the base units for length, mass, and temperature.
TABLE 1.4). In this chapter we will consider the base units for length, mass, and temperature.
TABLE 1.4 • SI Base Units
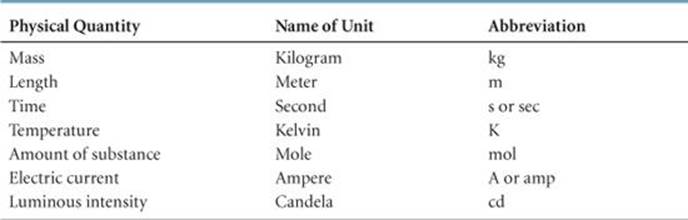
TABLE 1.5 • Prefixes Used in the Metric System and with SI Units
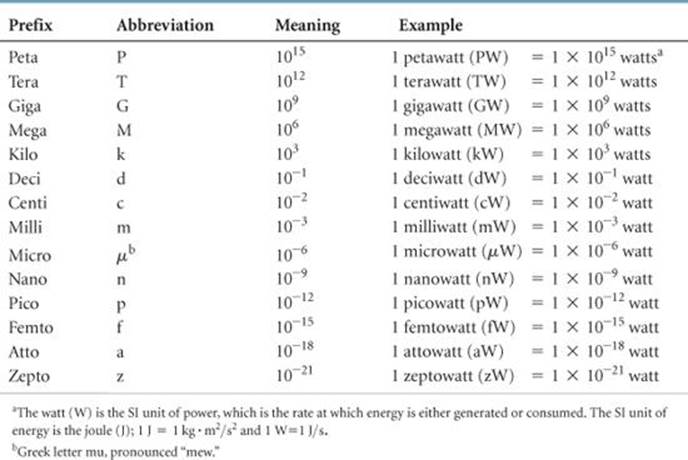
With SI units, prefixes are used to indicate decimal fractions or multiples of various units. For example, the prefix milli- represents a 10–3 fraction, one-thousandth, of a unit: A milligram (mg) is 10–3 gram (g), a millimeter (mm) is 10–3 meter (m), and so forth. ![]() TABLE 1.5 presents the prefixes commonly encountered in chemistry. In using SI units and in working problems throughout this text, you must be comfortable using exponential notation. If you are unfamiliar with exponential notation or want to review it, refer to Appendix A.1.
TABLE 1.5 presents the prefixes commonly encountered in chemistry. In using SI units and in working problems throughout this text, you must be comfortable using exponential notation. If you are unfamiliar with exponential notation or want to review it, refer to Appendix A.1.
Although non–SI units are being phased out, some are still commonly used by scientists. Whenever we first encounter a non–SI unit in the text, the SI unit will also be given. The relations between the non–SI and SI units we will use most frequently in this text appear on the back inside cover. We will discuss how to convert from one to the other in Section 1.6.
![]() GIVE IT SOME THOUGHT
GIVE IT SOME THOUGHT
Which quantity is the smallest: 1 mg, 1 μg, or 1 pg?
Length and Mass
The SI base unit of length is the meter, a distance slightly longer than a yard. Mass* is a measure of the amount of material in an object. The SI base unit of mass is the kilogram (kg), which is equal to about 2.2 pounds (lb). This base unit is unusual because it uses a prefix, kilo-, instead of the word gram alone. We obtain other units for mass by adding prefixes to the word gram.
SAMPLE EXERCISE 1.2 Using SI Prefixes
What is the name of the unit that equals (a)10–9 gram, (b)10–6 second, (c)10–3 meter?
SOLUTION
We can find the prefix related to each power of ten in Table 1.5: (a) nanogram, ng, (b) microsecond, μs, (c) millimeter, mm.
PRACTICE EXERCISE
(a) How many picometers are there in one meter? (b) Express 6.0 × 103 using a prefix to replace the power of ten. (c) Use exponential notation to express 4.22 mg in grams. (d) Use decimal notation to express 4.22 mg in grams.
Answers: (a)1012 pm, (b)6.0 km, (c)4.22 × 10–3 g, (d)0.00422 g
Temperature
Temperature, a measure of the hotness or coldness of an object, is a physical property that determines the direction of heat flow. Heat always flows spontaneously from a substance at higher temperature to one at lower temperature. Thus, we feel the influx of heat when we touch a hot object, and we know that the object is at a higher temperature than our hand.
The temperature scales commonly employed in science are the Celsius and Kelvin scales. The Celsius scale was originally based on the assignment of 0 °C to the freezing point of water and 100 °C to its boiling point at sea level (![]() FIGURE 1.17).
FIGURE 1.17).
The Kelvin scale is the SI temperature scale, and the SI unit of temperature is the kelvin (K). Zero on the Kelvin scale is the lowest attainable temperature, –273.15 °C, referred to as absolute zero. The Celsius and Kelvin scales have equal-sized units—that is, a kelvin is the same size as a degree Celsius. Thus, the Kelvin and Celsius scales are related according to
![]()
The freezing point of water, 0 °C, is 273.15 K (Figure 1.17). Notice that we do not use a degree sign (°) with temperatures on the Kelvin scale.
The common temperature scale in the United States is the Fahrenheit scale, which is not generally used in science. Water freezes at 32 °F and boils at 212 °F. The Fahrenheit and Celsius scales are related according to
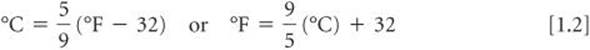
![]() GO FIGURE
GO FIGURE
True or false: The “size” of a degree on the Celsius scale is the same as the “size” of a degree on the Kelvin scale.
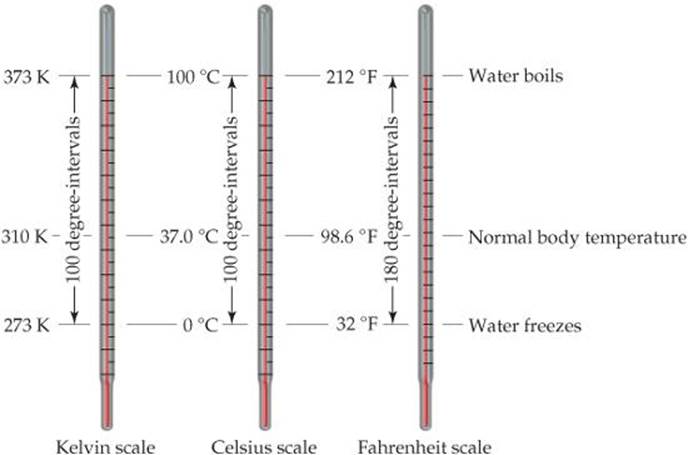
![]() FIGURE 1.17 Comparison of the Kelvin, Celsius, and Fahrenheit temperature scales.
FIGURE 1.17 Comparison of the Kelvin, Celsius, and Fahrenheit temperature scales.
SAMPLE EXERCISE 1.3 Converting Units of Temperature
A weather forecaster predicts the temperature will reach 31 °C. What is this temperature (a) in K, (b) in °F?
SOLUTION
(a) Using Equation 1.1, we have K = 31 + 273 = 304 K.
(b) Using Equation 1.2, we have ![]() .
.
PRACTICE EXERCISE
Ethylene glycol, the major ingredient in antifreeze, freezes at –11.5 °C. What is the freezing point in (a) K, (b) °F?
Answers: (a) 261.7 K, (b) 11.3 °F
Derived SI Units
The SI base units are used to obtain derived units. To do so, we use the defining equation for the quantity, substituting the appropriate base units. For example, speed is defined as the ratio of distance traveled to elapsed time. Thus, the SI unit for speed—m/s, read “meters per second”—is a derived unit, the SI unit for distance (length), m, divided by the SI unit for time, s. Two common derived units in chemistry are those for volume and density.
Volume
The volume of a cube is its length cubed, (length)3. Thus, the derived SI unit of volume is the SI unit of length, m, raised to the third power. The cubic meter, m3, is the volume of a cube that is 1 m on each edge (![]() FIGURE 1.18). Smaller units, such as cubic centimeters, (sometimes written cc), are frequently used in chemistry. Another volume unit used in chemistry is the liter (L), which equals a cubic decimeter, dm3, and is slightly larger than a quart. (The liter is the first metric unit we have encountered that is not an SI unit.) There are 1000 milliliters (mL) in a liter, and 1 mL is the same volume as 1 cm3:1 mL = 1 cm3. The devices used most frequently in chemistry to measure volume are illustrated in
FIGURE 1.18). Smaller units, such as cubic centimeters, (sometimes written cc), are frequently used in chemistry. Another volume unit used in chemistry is the liter (L), which equals a cubic decimeter, dm3, and is slightly larger than a quart. (The liter is the first metric unit we have encountered that is not an SI unit.) There are 1000 milliliters (mL) in a liter, and 1 mL is the same volume as 1 cm3:1 mL = 1 cm3. The devices used most frequently in chemistry to measure volume are illustrated in ![]() FIGURE 1.19.
FIGURE 1.19.
![]() GO FIGURE
GO FIGURE
How many 1-L bottles are required to contain 1 m3 of liquid?
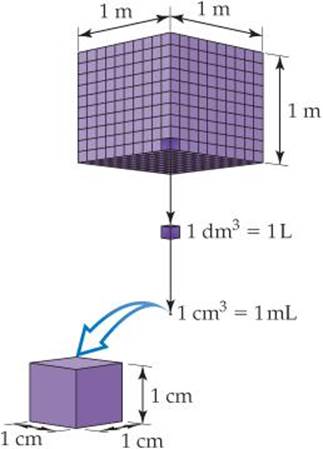
![]() FIGURE 1.18 Volume relationships. The volume occupied by a cube 1 m on each edge is one cubic meter, 1 m3. Each cubic meter contains 1000 dm3. One liter is the same volume as one cubic decimeter, 1L = 1 dm3. Each cubic decimeter contains 1000 cubic centimeters, 1 dm3 = 1000 cm3. One cubic centimeter equals one milliliter, 1 cm3 = 1 mL.
FIGURE 1.18 Volume relationships. The volume occupied by a cube 1 m on each edge is one cubic meter, 1 m3. Each cubic meter contains 1000 dm3. One liter is the same volume as one cubic decimeter, 1L = 1 dm3. Each cubic decimeter contains 1000 cubic centimeters, 1 dm3 = 1000 cm3. One cubic centimeter equals one milliliter, 1 cm3 = 1 mL.

![]() FIGURE 1.19 Common volumetric glassware.
FIGURE 1.19 Common volumetric glassware.
Syringes, burets, and pipets deliver amounts of liquids with more precision than graduated cylinders. Volumetric flasks are used to contain specific volumes of liquid.
![]() GIVE IT SOME THOUGHT
GIVE IT SOME THOUGHT
Which of the following quantities represents volume measurements: 15m2; 2.5 × 102m3; 5.77 L/s? How do you know?
Density
Density is defined as the amount of mass in a unit volume of a substance:
![]()
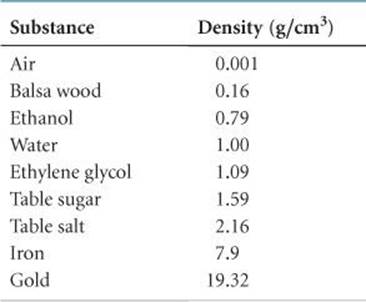
The densities of solids and liquids are commonly expressed in either grams per cubic centimeter (g/cm3) or grams per milliliter (g/mL). The densities of some common substances are listed in ![]() TABLE 1.6. It is no coincidence that the density of water is 1.00 g/mL; the gram was originally defined as the mass of 1 mL of water at a specific temperature. Because most substances change volume when they are heated or cooled, densities are temperature dependent, and so temperature should be specified when reporting densities. If no temperature is reported, we assume 25 °C, close to normal room temperature.
TABLE 1.6. It is no coincidence that the density of water is 1.00 g/mL; the gram was originally defined as the mass of 1 mL of water at a specific temperature. Because most substances change volume when they are heated or cooled, densities are temperature dependent, and so temperature should be specified when reporting densities. If no temperature is reported, we assume 25 °C, close to normal room temperature.
The terms density and weight are sometimes confused. A person who says that iron weighs more than air generally means that iron has a higher density than air—1 kg of air has the same mass as 1 kg of iron, but the iron occupies a smaller volume, thereby giving it a higher density. If we combine two liquids that do not mix, the less dense liquid will float on the denser liquid.
TABLE 1.6 • Densities of Selected Substances at 25 °C
SAMPLE EXERCISE 1.4 Determining Density and Using Density to Determine Volume or Mass
(a) Calculate the density of mercury if 1.00 × 102 g occupies a volume of 7.36 cm3.
(b) Calculate the volume of 65.0 g of liquid methanol (wood alcohol) if its density is 0.791 g/mL.
(c) What is the mass in grams of a cube of gold (density = 19.32 g/cm3) if the length of the cube is 2.00 cm?
SOLUTION
(a) We are given mass and volume, so Equation 1.3 yields 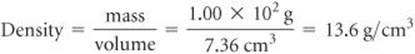
(b) Solving Equation 1.3 for volume and then using the given mass and density gives 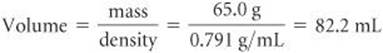
(c) We can calculate the mass from the volume of the cube and its density. The volume of a cube is given by its length cubed: Volume = (2.00 cm)3 = (2.00)3 cm3 = 8.00 cm3
Solving Equation 1.3 for mass and substituting the volume and density of the cube, we have Mass = volume × density = (8.00 cm)3(19.32 g/cm3) = 155 g
PRACTICE EXERCISE
(a) Calculate the density of a 374.5-g sample of copper if it has a volume of 41.8 cm3. (b) A student needs 15.0 g of ethanol for an experiment. If the density of ethanol is 0.789 g/mL, how many milliliters of ethanol are needed? (c) What is the mass, in grams, of 25.0 mL of mercury (density = 13.6 g/mL)?
Answers: (a) 8.96 g/cm3, (b) 19.0 mL, (c) 340 g
 CHEMISTRY PUT TO WORK
CHEMISTRY PUT TO WORK
Chemistry in the News
Because chemistry is so central to our lives, reports on matters of chemical significance appear in the news nearly every day. Some reports tell of breakthroughs in the development of new pharmaceuticals, materials, and processes. Others deal with energy, environmental, and public safety issues. As you study chemistry, you will develop the skills to better understand the importance of chemistry in your life. Here are summaries of a few recent stories in which chemistry plays a role.
Biofuels Reality Check
With the Energy Policy Act of 2005, the US Congress gave a big push to fuels derived from biomass (plants or algae) as a renewable alternative to gasoline. The 2005 act was followed by the Energy Independence and Security Act of 2007, which required that 9.0 billion gallons of renewable fuel be used in gasoline in 2008, 11.1 billion gallons in 2009, and 36 billion gallons by 2022. The United States currently consumes about 140 billion gallons of gasoline per year.
Ethanol derived from corn currently dominates the alternatives, with 40% of all gasoline now containing some ethanol. A blend of 10% ethanol and 90% gasoline, called E10, is the most common blend because it can be used in virtually all vehicles. Blends of 85% ethanol and 15% gasoline, called E85, are also available but can be used only with specially modified engines (![]() FIGURE 1.20).
FIGURE 1.20).

![]() FIGURE 1.20 A gasoline pump that dispenses E85, a mixture of 85% ethanol and 15% gasoline.
FIGURE 1.20 A gasoline pump that dispenses E85, a mixture of 85% ethanol and 15% gasoline.
However, using a food crop to produce transportation fuel may not be the best long-term solution for the energy problem. In 2006, researchers at the University of Minnesota calculated that “even dedicating all US corn and soybean production to biofuels would meet only 12% of gasoline and 6% of diesel demand.” The conversion of a much wider range of plant material, using a much greater fraction of available plant matter, into fuels will be necessary to improve these numbers substantially. Because the most abundant plant material, cellulose, does not readily convert to ethanol, a great deal of research will be needed to solve this challenging problem. Meanwhile, it is worth reflecting that a 3% improvement in vehicle fuel efficiency would displace more gasoline use than the entire 2006 US ethanol production. An alternative to ethanol relies on coaxing microorganisms to produce molecules that can be used as fuel. In 2009, ExxonMobil Research and Engineering Company partnered with a start-up company, Synthetic Genomics, to find strains of photosynthetic algae that will efficiently produce oils and hydrocarbons from sunlight and carbon dioxide.
Advances in Solar Energy
In the 1970s, at the height of the oil crisis, there was a burst of research on renewable energy, including solar energy. After the oil crisis passed and gasoline was once again cheap and readily available, solar energy research was less of a priority. With the more recent increase in gasoline prices and a greater realization that the burning of fossil fuels contributes to global warming, solar energy research is again in vogue. The amount of solar radiation reaching Earth every day is enormous, and if we could harness it efficiently, our energy needs could be easily met. Solar panels like those shown in Figure 1.2a are about 10% efficient in converting light directly into electricity. However, storage of solar energy remains a vigorous area of research: How can we capture solar energy for use when the Sun is not shining? One potential answer is to store the energy in chemical bonds. One promising new material, first reported in 2008, is a cobalt-containing compound that can convert water into oxygen with sunlight. Hydrogen can also be generated in sunlight from water but using a different compound to facilitate the reaction. Electricity can then be produced by combining the hydrogen and oxygen in a fuel cell.
Important Antibiotic Modified to Combat Bacterial Resistance
Vancomycin is an antibiotic of last resort—used only when other antibacterial agents are ineffective. Some bacteria have developed resistance to vancomycin, causing researchers to modify the molecular structure of the substance to make it more effective in killing bacteria. This approach was based on the knowledge that vancomycin works by binding to a protein that is essential to forming bacterial cell walls. Researchers have synthesized a vancomycin analog in which a CO group has been converted to a CH2 group (![]() FIGURE 1.21). This modification increases the compound's binding affinity in the cell walls of vancomycin-resistant bacteria, making the analog 100 times more active than vancomycin against vancomycinresistant bacteria.
FIGURE 1.21). This modification increases the compound's binding affinity in the cell walls of vancomycin-resistant bacteria, making the analog 100 times more active than vancomycin against vancomycinresistant bacteria.

![]() FIGURE 1.21 Comparing CO and CH2 groups. The molecule on the left contains a CO group, and the one on the right contains a CH2 group. This subtle difference is similar to how the structure of the much more complex vancomycin molecule was modified.
FIGURE 1.21 Comparing CO and CH2 groups. The molecule on the left contains a CO group, and the one on the right contains a CH2 group. This subtle difference is similar to how the structure of the much more complex vancomycin molecule was modified.
Replacing the Lightbulb through Chemistry
If you want to save the world from global warming, you can start by replacing incandescent lightbulbs. In 2001 approximately 22% of all electricity generated in the United States was used for lighting. This surprisingly high number is due in part to the fact that incandescent lights convert only 5% of the energy supplied to them into visible light and last only 1000 hours on average. Compact fluorescent lamps are more efficient (20% of their output energy is converted into visible light) and last longer (up to 15,000 hours), but they contain mercury, which is toxic and creates disposal problems. A promising replacement bulb is the light-emitting diode (LED). Red LEDs were first made in 1962. As a result of subsequent increases in efficiency and development of other colors, LEDs are now used in traffic lights, car taillights, and a host of electronics applications. These “solid state” devices do not contain mercury, can achieve efficiencies as high as 50%, and hold the promise of longer lifetimes (red LEDs last up to 100,000 hours). With advances in research and development, costs are coming down to the point that some small cities are replacing their streetlights with white LEDs (![]() FIGURE 1.22).
FIGURE 1.22).

![]() FIGURE 1.22 LED lighting. Ann Arbor, Michigan, has replaced incandescent streetlights with white LEDs. The city estimates the change will save $100,000 per year and reduce annual greenhouse gas emissions by 267 tons.
FIGURE 1.22 LED lighting. Ann Arbor, Michigan, has replaced incandescent streetlights with white LEDs. The city estimates the change will save $100,000 per year and reduce annual greenhouse gas emissions by 267 tons.