CHEMICAL BIOLOGY
Molecular Recognition, Computation and Modeling of
Anna Feldman-Salit and Rebecca C. Wade, EML Research, Heidelberg, Germany
doi: 10.1002/9780470048672.wecb354
Molecular recognition is critical to many fundamental processes in biology, including enzymatic reactions, signal transduction, genetic information processing, as well as molecular and cellular transport. The question of how proteins selectively recognize and correctly associate with their partners is an active research problem. For many proteins, experimental information about the structures of their molecular complexes and the details of their interactions are lacking. Macromolecular, structure-based computational techniques provide a means to predict the interactions of proteins and to investigate their recognition mechanisms. Here, we first discuss the general mechanism of molecular recognition as a multistep process from diffusion of one molecule toward the second to tight complex formation. We then describe the main forces and the physical properties that govern biomolecular interactions and introduce the principles of modeling them. Finally, simulation methods and computational approaches for molecular docking are briefly presented.
An understanding of the mechanisms of molecular recognition provides the essential basis for rational structure-based drug design and bioengineering. However, biomolecular recognition is complex and is determined by a fine balance between different contributing properties such as shape, electrostatics, dynamics, and entropy. This complexity makes the modeling of biomolecular recognition and the prediction of the properties of biomolecular complexes challenging. Here, we first discuss the factors important for biomolecular recognition that should be considered in computational models. Then simulation methods, such as Brownian and Molecular Dynamics, as well as other computational techniques that are widely exploited for studying protein-protein and protein-ligand recognition are presented. Last, we describe the principles, approximations, and limitations of some existing computational molecular docking approaches, which provide a means to predict the structures of bound complexes.
Biological Background
Molecular recognition is one of the most fundamental and important processes in biology. It occurs between two or more molecules, and it is involved in biochemical processes such as enzymatic reactions, molecular transport in the cell, genetic information processing, and protein assembly.
Although molecular recognition is of importance to all biomolecules, the astounding molecular recognition properties of the immune system have been the subject of investigations since the nineteenth century. It is intriguing how a vast number of chemically similar antibodies are serologically indistinguishable but can react with different antigens can be produced in one species (1). Similarly, the major histocompatability complex can recognize a huge variety of peptides. How the immune system achieves this spectrum of molecular recognition properties is still not fully understood. Nevertheless, studies of this molecular recognition process have been exploited practically, namely in the design of vaccines that exploit the molecular recognition between antibodies and cell surface antigens.
The recognition between proteins and nucleic acids has challenged scientists for a long time. RNAs, for example, are capable of enzymatic activity and make direct contributions to substrate recognition and catalysis in ribonucleoproteins such as the ribosome (2) and the spliceosome (3). Nearly all the functions of RNAs are associated with the binding of proteins. However, the question of how a protein recognizes a specific RNA site, what effects it has on the RNA structure and dynamics, and how it promotes a specific RNA function are still very demanding. It is, for example, of great interest to understand how aminoacyl-tRNA synthetases achieve the specificity needed to ensure faithful translation of the genetic code.
An understanding of molecular recognition is of clear importance for structure-based drug design and bioengineering. Different aspects of molecular recognition can be studied by experimental techniques such as yeast two-hybrid, surface-plasmon resonance, atomic force microscopy, X-ray crystallography, NMR spectroscopy, electron microscopy, and isothermal titration calorimetry (4-10). The ability to model and simulate molecular recognition in a computational manner is complementary to these experimental approaches; it is not only important for gaining a fundamental understanding of molecular recognition processes, but also it is of crucial importance for applications such as the design of drugs.
Mechanisms of Molecular Recognition
The mechanism of molecular recognition can be described schematically as a multistep process. Two molecules first come into proximity from afar. If active transport does not occur, then this process will occur by diffusional association with formation of a diffusional encounter complex, which is a loose complex between the molecules. Depending on the degree of burial of the binding sites, diffusion may occur of a small molecule through its macromolecular receptor to the binding site and this may require conformational changes in the receptor. Finally, and usually after induced fit conformational changes, the molecules will form a fully bound complex (11). The extent to which induced fit exists as opposed to selection of a binding conformation among a conformational ensemble of a protein is the subject of debate (12); but presumably, it varies according to the system, as does the extent of conformational change.
The binding process may be mediated first by long-range electrostatic interactions between the two associating molecules and then complemented by short-range van der Waals interactions and hydrogen bonding. Water molecules can either be displaced on binding or retained to mediate binding of the molecules. The forces involved in the process of molecular recognition are discussed in more detail later.
Kinetics and thermodynamics of molecular recognition
The rate of binding of two molecules A and B and formation of their complex AB can be quantified by the bimolecular association rate constant (on-rate constant), kon, whereas their unbinding is characterized by the dissociation rate constant (off-rate constant), koff.
![]()
The binding affinity of two molecules can be quantified by the equilibrium dissociation constant, Kd,
![]()
With the relation between Kd and the binding free energy (Gibb’s energy), ∆G, Kd can be expressed as
![]()
where R is the universal gas constant (~8.31 JK-1 mol-1), T is the temperature in K, and C0 is the standard concentration. The dissociation constant is usually given in molar units (M).
The binding free energy ∆G is defined by the interplay between two thermodynamic entities: binding enthalpy, ∆H, and binding entropy, ∆S.
![]()
The phenomenon of “enthalpy-entropy compensation,” in which one term favors binding and the other term disfavors binding, is observed for many molecular recognition processes. On one hand, the binding benefits from enthalpic contributions that include electrostatic, hydrogen bonding, and van der Waals interactions. On the other hand, the unfavorable loss of translational and rotational entropy occurs mainly due to the reduction in the number of degrees of freedom of the molecules on their complexation. Bimolecular binding is also disfavored by the loss of flexibility of the molecules on binding, although it can benefit from increased flexibility at a distance from the binding sites (allosteric effect). The displacement of water molecules on binding may also be entropically favorable. Different sources of entropic contributions to binding are discussed later (see the section entitled “Entropy”).
Conformational changes on binding
The conformational flexibility of the molecules plays a very important part in their binding. When a protein-protein complex is modeled using the structures of the two proteins determined in their unbound states, some key side chains or structural motifs might be positioned to result in steric clashes or unfavorable electrostatic interactions (13, 14). Therefore, on binding, the intermolecular interactions should result in some degree of induced fit. Induced fit can be defined as the collection of conformational changes, which results in optimal interactions, when two molecules come into contact (14).
These conformational changes in biomolecules can vary from small-scale motions, which include bond stretching, bond angle bending, and dihedral angle variations, to larger motions of the main chain, which are the loops or entire domains of proteins. Such changes occur on different timescales, which range from picoseconds to hours, with amplitudes that extend to hundreds of Angstroms (15). Small changes in molecular conformation can adversely affect molecular docking results when using rigid molecular models. For example, Betts and Sternberg (16) have found that RMS deviations of 0.6 A for backbone and 1.7 A for side chain atoms affect protein-protein docking.
The dynamics of protein side chains occurs on the time scale of picoseconds to milliseconds with RMS deviations up to about 5 A. Such motions include the rotation of side chains between different rotamers. A “flexibility scale” for protein side chains has been determined (17). It is known that protein-protein interactions are critically dependent on “hot-spot” residues at the binding interface (18). Molecular dynamic simulations have revealed that the hot-spot residues are found frequently in the unbound proteins in the rotamers observed in the protein-protein complex (19, 20). In contrast, the side chains at the perimeter of the interface are mostly found in nonspecific rotamers in the unbound protein, which suggests that their final conformations are induced on binding. It was proposed by Kimura et al. (19) that these side chains act more as “latches” that hold the molecules together rather than as “keys” fitting snugly into the binding pocket. According to the mechanism of induced fit, these latches open before docking and “fasten” to their partners later during the binding process.
The conformational rearrangements of backbone atoms and of protein loops play a significant role in ligand recognition, protein-protein association, DNA-binding, and so on (21-24). For developing the docking methodology, Chen et al. (25) and Vajda et al. (26) classified 59 protein complexes based on their docking difficulty. The cases in which substantial conformational changes of the backbone or loops between the unbound and bound structures were observed were referred to as “difficult.” Such backbone motion may be up to 10 A or more and can drastically modify the steric and the electrostatic properties of the protein face presented to the partner. In some cases, loop motion may be caused by large changes in as few as two torsion angles (27), but sometimes the deformations are distributed over more torsion angles (28, 29).
Large-scale domain or subunit motions are often classified into hinge and shear motions (30). Short loops or elements of secondary structure can serve as hinge regions. Interactions of ligands with bending domains may cause the protein to undergo certain conformational changes, which sometimes leads to closure of a binding site, see Fig. 1.
The extent and the variation of the conformational changes that can occur on molecular binding show the necessity for these changes to be taken into account when modeling the molecular recognition and the binding of two associating molecules.

Figure 1. Illustration of conformational changes as result of ligand binding into the pocket of Salmonella typhimurium O-Acetyl-Serine Sulfhydrylase (OASS). The partial representation of the OASS structure in the absence of the ligand (methionine) is shown in light rendering (PDB entry 1OAS); the corresponding structure of OASS in the presence of the ligand is shown in dark rendering (PDB entry 1D6 S). The ligand is represented by spheres. The binding of the ligand induces conformational changes, which lead to the closure of the binding site. It includes a large-scale motion of the upper domain of OASS toward the binding site, conformational change of the loop hindering the binding site, and the change in conformation of a side-chain (Asparagine). The asparagine adopts a different rotamer state on induced fit, which forms a hydrogen-bond with an oxygen atom of the ligand.
Modeling Molecular Recognition
Modeling of the different steps of molecular recognition requires suitable models of the corresponding forces and the energetic contributions. These elements will be considered in the next section.
Shape complementarity and van der waals interactions
In 1894, Emil Fischer postulated that bimolecular recognition is analogous to the matching of a “key” into its “lock,” in which the “lock” refers to an enzyme and the “key” refers to a substrate. Only the correctly shaped key (substrate) fits into the hole (active site) of the lock (enzyme). Describing molecular recognition in terms of structure and bonding in the mid-1940s, Pauling defined the specificity of bimolecular recognition, which occurs due to the mutually complementary configurations of molecular surfaces. In other words, the surface of one molecule conforms closely to the surface of the other molecule on bimolecular binding.
Molecular shape complementarity is critical to biomolecular recognition and specificity. Even if the molecules change conformation on binding and water molecules are trapped at the interface, bound complexes show high shape complementarity (31). This shape complementarity is dependent on van der Waals interactions between the binding molecules. Electron-electron repulsion prevents atomic overlap and intermolecular penetration. However, induced dipole effects as atoms approach lead to short-range attractive interactions.
The simplest approximation in modeling molecular recognition is to model just van der Waals repulsion by preventing steric overlap (e.g., with an infinite wall potential or a geometric shape description). The short-range attraction is usually accounted for in modeling biomacromolecules with an empirical energy function by means of a Lennard-Jones energy (32, 33):
![]()
where the first term describes the attraction and the second term describes the repulsion between a pair of interacting atoms where rij is the distance between them. The coefficients C and D depend on the type of the atoms and Dij = 0.5 Cij (rij0)6, where rij0 is the sum of the van der Waals radii of atoms i and j. Cij is parameterized according to the Slater-Kirkwood equation based on atomic polarizability and the number of outer-shell electrons of interacting atoms (34, 35). For computational convenience, Lennard-Jones energies and forces are often computed only for pairs of atoms within a defined “cutoff” radius of about 10 A (35).
Electrostatic interactions
Electrostatic interactions are long range, vary with distance as 1/r, and play a significant role in molecular recognition. Therefore, they are particularly important to model when simulating the initial diffusional step of biomolecular recognition. Molecules are characterized not only by their net charges, but also by their charge distributions. For modeling electrostatic interactions, formal or partial charges are assigned to the atoms of the interacting molecules. The simplest model to describe the interactions between charges is Coulomb’s law, in which the electrostatic energy Eel of charges qiA in molecule A and qjB, in molecule B is given by
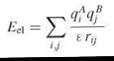
where rij is the distance between atoms i and j, and ε is the dielectric constant. The potential of a charge qi at the position of atom j at distance rij in homogeneous dielectric ε is Ф = qi/εrij.
Weaker electrostatic interactions occur in a polar medium such as water rather than in vacuum because of dielectric screening. If the atoms in the system, including the water molecules and ions of the solvent, are modeled explicitly, then a relative dielectric constant εr is usually assigned as 1 (ε = ε0εr, where ε0 is the permittivity of free space). However, when the molecules and the medium are treated implicitly, the relative dielectric constant is used as a descriptor of the bulk polarizability of the medium. Proteins tend to have a lower relative dielectric constant than water because many dipolar groups can be considered frozen into a hydrogen-bonded lattice and therefore cannot reorient in an external electrostatic field. Typical assignments of the εr for proteins range from 2 to 20. Water, however, has a high εr around 80 because its dipoles can reorient freely. This dielectric heterogeneity should be accounted for in an electrostatic model of a system with protein molecule(s) in water.
The Poisson equation (or Gauss’ Law) describes the electrostatic potential of a fixed charged density of the solute ρsoute(r). The exterior charge density of the ions in the solution, ρexterior(r) is modeled by assuming a Boltzmann distribution. The Poisson-Boltzmann (PB) equation is commonly applied to molecules in aqueous solution to compute the electrostatic potential of the system. The general form of the PB equation is
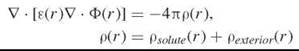
where Ф(r) is the electrostatic potential at position r; ε(r) is the position-dependent dielectric function; ρ(r) is given by the charge density of the solute, ρsoute(r), and of the ions in the solvent, ρexterior(r); and ![]() designates the vector differential operator.
designates the vector differential operator.
The PB equation may be solved numerically for macromolecules (for reviews, see References 36-38. The finite difference, finite element, and multigrid methods are used most commonly to solve the PB equation. Usually, this technique is performed by mapping the molecules onto a three-dimensional cubic grid. To solve the PB equation, a suitable interior relative dielectric constant and definition of the dielectric boundary should be assigned (39, 40).
Hydrogen bonding
Hydrogen bonds are specific, short-range, nonbonded interactions. They occur between a proton donor of strongly polar groups such as FH, OH, NH, and SH, and a proton acceptor that is strongly electronegative such as F, O, or N. Weak hydrogen bonds may also be formed by CH groups. The “attraction” of the proton has electrostatic nature. However, quantum-mechanical treatments reveal other contributions to hydrogen bonds. These treatments include the short range repulsion due to the smaller distance between acceptor and hydrogen donor than the sum of their van der Waals radii and the attraction that originates from charge transfer (for review, see Reference 41).
Several empirical analytic forms for the energy of a hydrogen bond have been proposed. A general expression for the energy of a hydrogen bond that describes their directional properties is:
![]()
The distance-dependent term may have values of m and n of 10 and 12 or 6 and 8, respectively, [e.g., the latter are used in the GRID program (42)]. The angular terms are functions of the angles made at the donor hydrogen and at the acceptor atom and depend on the chemical types and bonding of the hydrogen bonding atoms.
Hydrogen bonds play an essential role in the stabilization of secondary structures in proteins and in the interactions of macromolecules. In proteins, hydrogen bonds “lock” secondary structure elements such as a-helices, beta-sheets, and beta-turns. Most hydrogen bonds occur between N-H and O=C groups in the polypeptide chain. Because of the strong hydrogen bonding abilities of water molecules to polar groups in proteins, it is believed that the structural water molecules tighten the protein matrix. However, evidence has been provided for the importance of structural water molecules in increasing protein flexibility (43).
Hydrogen bonds are of great importance for the specificity of molecular recognition at short range. Unsatisfied hydrogen bonding at the binding interface of two interacting macromolecules will disfavor binding. The charged or polar residues at the binding interface of one macromolecule can form hydrogen bonds to charged groups or to polar groups of another macromolecule. Interfacial water molecules may also mediate molecular recognition, due to their ability to donate and accept hydrogen bonds. They can improve the hydrogen bonding at the interface of two interacting molecules or facilitate conformational changes. In simulations, to observe optimal hydrogen bonding in proteins or between them on binding, it is often important to include water molecules explicitly in the system (35).
Hydrophobic effect
The hydrophobic effect refers to the favorable interactions between nonpolar surfaces immersed in water. These interactions are considered to provide the driving force for protein folding (44) and to make a major contribution to the stability of protein tertiary structures. The hydrophobic effect also plays an important role in protein interactions (45). The hydrophobicity of protein surfaces has been studied experimentally by affinity partitioning of proteins (46). Theoretical studies have shown that the presence of hydrophobic patches on the surfaces of proteins correlates with protein binding sites (47-49).
In simulations with explicit water molecules, the hydrophobic interactions must result from a complicated interplay of Lennard-Jones and electrostatic interactions between the atoms of the proteins and the surrounding water molecules. In the case that the water is represented implicitly, the hydrophobic interactions are usually modeled by an empirical term that depends on the surface area buried on binding:
![]()
where SASA indicates the solvent accessible surface area, and O is a coefficient that depends on the surface area definition and the atom type (50). The SASA was described first by Lee and Richards in 1971 (51). For computational calculations, the “rolling ball” algorithm of Shrake and Rupley is often used (52). The ball or sphere radius is typically 1.4 A, which approximates the radius of a water molecule.
The buried surface area between two interacting molecules, A and B, is calculated as the difference between the summated SASA of each molecule separately and SASA of the complex:
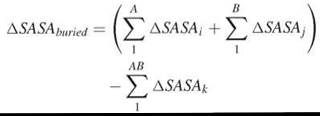
Entropy
Many biological processes such as protein folding, molecular recognition, or more specifically ligand-protein or protein- protein binding, are associated with changes in entropy. Entropy is defined as a measure of “freedom” of the system. Several types of entropy are involved in recognition processes.
On bimolecular binding, an entropic loss develops from the reduction of the translational (Strans) and rotational (Srot) freedom because of the transformation of two unbound molecules into one bound complex. Strans and Srot for the gas phase may be calculated by the “Sackur-Tetrode” approach (53). Modifications are required to estimate Strans and Srot in other environments (54).
In addition, the loss in Strans and Srot has been found to be compensated largely by intermolecular, mostly vibrational, motions (Sres) in the complex. Sres is expected to be smaller for high affinity complexes and larger for low affinity complexes (55). Sres can be estimated using harmonic or quasiharmonic models of the system (for more details, see Reference 56).
Intuitively, binding is expected to restrict the flexibility of both partners and lead to a significant loss in conformational entropy. To overcome this unfavorable loss of conformational entropy, specific and favorable intramolecular or short-range intermolecular interactions such as hydrogen bonds, salt bridges, hydrophobic interactions and so on are formed. In some cases, the binding of the partners causes increased conformational flexibility of regions distant from the actual binding site, which results in allosteric effects (57). The change in conformational entropy due to the protein backbone and side chains is usually estimated by considering the protein as having discrete, isoenergetic, conformational states (e.g., side chain rotamers). Then:
![]()
where n indicates the number of states, and 1 and 2 refer to the initial and final situations. The conformational entropy (Sconf) is often subdivided into backbone (Sback) and side chain (Sside) entropies. ∆Sback is determined by the probability distribution over the dihedral angle space. The contribution of backbone entropy is generally less significant for binding than for folding. ∆Sside is usually estimated by rotamer counting, although more detailed probability calculations can be performed (also discussed in Reference 58).
During molecular binding, some water molecules are “released” from the interface of the contacting molecules, which causes a favorable entropic contribution, ∆Ssolv. The solvation entropy is commonly computed using methods based on solvent accessible surface areas (SASA) (58, 59). However, when binding involves highly charged molecules such as nucleic acids, the SASA approach may not be adequate. Because of the presence of highly charged binding partners in the solvent, additional solvation entropy contributions (∆Sdielectric and ∆Sionic) should be taken into consideration. These contributions result from ordering of the water dipoles via long-range electrostatic interactions and the formation of an ionic atmosphere. Sharp et al. (60) calculated ∆Sdielectric and ∆Sionic using a Poisson-Boltzmann model in conjunction with van’t Hoff analysis and applied it to drug and protein binding to DNA. Water molecules may also be trapped at the interface with an entropic cost, which can be estimated by considering the loss of mobility of the water molecules compared to bulk solvent (61).
Simulation of Molecular Recognition
The techniques appropriate for simulating a molecular recognition process depend on the time and the spatial scales of the simulated process or step. Here, we first discuss the use of Brownian and molecular dynamics simulation methods and then discuss how the level of detail can be altered in constructing models for the simulation of molecular recognition.
Brownian dynamics simulation
The Brownian Dynamics (BD) simulation technique can be used to simulate the diffusion and the association of molecules in solution. BD simulations have been widely used to simulate protein-small molecule and protein-protein association (62). This method may be exploited to simulate the first step of molecular recognition when two molecules diffuse from a distance. From such simulations, it is possible to compute the structure and the diffusional encounter complex ensemble and to calculate the bimolecular association rate constant for two diffusing proteins or enzymes and their substrates or inhibitors. In these calculations, the effects of mutations and variations in ionic strength, pH, and viscosity can be investigated (63).
The general principle of BD is based on Brownian motion, which is the random movement of solute molecules in dilute solution that result from repeated collisions of the solute with solvent molecules. In BD, solute molecules diffuse under the influence of systematic intermolecular and intramolecular forces, which are subject to frictional damping by the solvent, and the stochastic effects of the solvent, which is modeled as a continuum. The BD technique allows the generation of trajectories on much longer temporal and spatial scales than is feasible with molecular dynamics simulations, which are currently limited to a time of about 10 ns for medium-sized proteins.
The basic BD algorithm developed by Ermak and McCammon (64) provides an approximate solution to the Langevin equation in the highly damped diffusive limit by using the positions of a solute particle at time t, together with the forces acting on them, to estimate the particle’s new position at time, t + ∆t. The translational behavior of the particle is described by:
![]()
where F is the force that acts on the particle, D is the translational diffusion constant of the particle, and R is a random displacement that mimics the effects of collisions of the particle with solvent molecules. The rotational behavior of the diffusing particle is described by a similar equation to the translational behavior. The translational and rotational diffusion constants of proteins can be estimated by the Stokes-Einstein relationship, which depends on the solvent viscosity and the radius of the protein. Larger proteins diffuse slower. The forces on a protein are typically calculated by solution of the Poisson-Boltzmann equation. Clashes between molecules are avoided by rejecting any time-step displacement that causes overlap and by proceeding with another stochastic step (defined by a different random number).
For simulation of molecular recognition by BD to compute association rate constants and for the generation of the structures of diffusional encounter complexes, the following setup may be used. One solute, which usually is the larger one, is positioned at the center of simulation space. The second molecule diffuses from randomly chosen starting points at a specified distance, and many trajectories are generated. The probability of formation of diffusional encounter complexes is computed from these simulations. The method of Northrup et al. (65) allows computation of the association rate constant by combining an analytical solution to the diffusion equation with the numerical data from the BD simulations.
The programs most widely used for simulation of the diffusional encounter of two biomolecules are UHBD (66, 67), Macrodox (68), and SDA (66, 67).
Molecular dynamics simulation
Molecular dynamics (MD) trajectories can be used to investigate the structure, dynamics, and thermodynamics of biological molecules and their complexes. The motions of the atoms in the system are simulated according to Newton’s equations of motion. The forces on the atoms are calculated using a molecular mechanics energy function. The force field for a protein is given by the sum of various components including bond stretching and bond angle bending, torsional potential, and nonbonded interactions (Lennard-Jones and Coulombic interactions). Several different algorithms may be used to generate snapshots of the system using a time step of about 1 fs (69, 70).
The motions of proteins are usually simulated in aqueous solvent. The water molecules can be represented either explicitly or implicitly. To include water molecules explicitly implies more time-consuming calculations, because the interactions of each protein atom with the water atoms and the water molecules with each other are computed at each integration time step. The most expensive part of the energy and force calculations is the nonbonded interactions because these scale as N2 where N is the number of atoms in the system. Therefore, it is common to neglect nonbonded interactions between atoms separated by more than a defined cut-off (~10 A). This cut-off is questionable for electrostatic interactions because of their 1/r dependence. Therefore, in molecular dynamics simulations, a Particle Mesh Ewald method is usually used to approximate the long-range electrostatic interactions (71, 72).
MD simulations are used mainly to investigate in detail the interactions of two associating macromolecules at relatively short distances, rather than to simulate their coming together from afar. Thus, an encounter complex or an approximate protein-ligand complex can be refined using MD simulations. Indeed, MD is an important tool in macromolecular complex structure determination in which it is used with simulated annealing and experimental constraints. Important applications of MD simulations include the computation of the binding free energies and intermolecular forces.
CHARMM, AMBER, GROMOS, GROMACS, Discover, and VMD/NAMD are some programs used widely to perform MD simulations (http://cmm.cit.nih.gov/modeling/software. html).
Coarse graining of a simulation model
Most biomolecular binding events occur on timescales orders of magnitude greater than can be attained in standard molecular dynamics simulations in which the motion of all atoms is simulated. One way to address this problem is to simplify the description of the molecular system by so-called “coarse graining.” Both BD and MD can be performed with coarse-grained and atomistic detail models. A reduced protein model in which one pseudoatom represents one amino-acid residue has, for example, been used in protein-protein docking studies by Cherfils et al. (73). Zacharias (74), in his ATTRACT method for protein-protein docking, has used a reduced protein model with up to three pseudoatoms per residue. The interactions between pseudoatoms are calculated by using a soft Lennard-Jones-type potential with parameters that reflect the hydrophilic or hydrophobic character of the side chain. In coarse graining, the solvent may be treated either as a continuum or as coarse-grained [e.g., by representing four water molecules by one particle as performed in the Martini model (75)].
Coarse graining may be combined with a confinement of the conformational space by placing the coarse grain particles on a cubic lattice. For example, Kurcinski and Kolinski (76) (CABS-REMC) represented the polypeptide chains by strings of Ca beads on a cubic lattice. Side chains were represented by up to two interaction centers, which correspond to Cβ and the centers of mass of the remaining portions of the side groups, respectively. The conformational space of this model is sampled by means of a multicopy Monte Carlo method.
A major difficulty in creating coarse-grain models is their parameterization, which often requires detailed comparison with the results of all-atom simulations as well as experimental data. However, the advantage is not only that fewer degrees of freedom exist, but also that the energy landscape is generally smoother than in an all-atom model; therefore, it is easier to optimize configurations.
Molecular Docking: Prediction of Bound Complexes
Whereas dynamic simulations may be used to study the process of molecular binding and unbinding and to predict the structure of the bound complex, many computations are aimed solely at prediction of the structure of the bound complex. This is the so-called “docking problem.” Although this problem can be addressed by using simulations to mimic the physical binding process (77), many other approaches may be used to sample molecular arrangements and to predict the bound complex. Energy minimization from systematically or randomly distributed starting arrangements may be performed subject to a detailed or simplified force field [e.g., for protein-protein docking, (74)]. Simulated annealing and Monte Carlo methods include temperature to permit high-energy configurations to be sampled and thereby energy barriers to be overcome [e.g., AutoDock, (78)]. Genetic algorithms and particle swarm optimization methods are biologically inspired procedures for optimizing a function efficiently that have been applied to small molecule docking [e.g., GOLD (79), PLANTS (80)] and to protein-protein docking (81). They may be applied with driving “forces” for binding that ranges from simple geometric complementarity (82) to detailed molecular mechanics type force fields. Systematic searching is widely used. This can be facilitated by FFT methods, which were applied initially to protein-protein docking by optimization of geometric fit (83). Because the direct calculation of the correlation between two functions results in an order of N6 computing steps, Katchalski-Katzir et al. (83) used Fourier Transforms to calculate the correlation function more rapidly. With this algorithm, the computing time is proportional to N3lnN3, where N is the number of atoms in the complex. FFT methods have been used to optimize not only geometric fit but also hydrophobicity complementarity (48) and electrostatic complementarity (DOT) (84).
Optimization may be performed in continuous or discrete space. For example, in optimizing the conformations of side chains in proteins, a discrete rotamer representation is often used. In 2003, Gray et al. (85) presented a docking program RosettaDock that allows the side chain conformations of the interface residues on both interacting partners to change. The side chain flexibility was modeled using a simulated annealing algorithm that searches through backbone-dependent rotamers from the Dunbrack rotamer library (86). The side chains of the partners are rebuilt from rotamers before docking (prepacking) and only the side chains of the interface are then refined later in docking. Additional improvements of this method, such as implementation of a torsion minimization step to sample off-rotamer space and information on side chain packing from the unbound structures, are described in Reference 87. However, in some cases, which may be binding hot spots, side chains adopt nonideal-rotamer conformations and these should be accounted for (88). In the ATTRACT approach of Zacharias (74), several conformations are considered for each side chain simultaneously. Side chain copy selection is coupled to energy minimization in translational and rotational degrees of freedom of the mobile protein partner in an iterative way. This technique is effective for complexes in which side chain conformational changes occur during complex formation. Similar to side chain mobility, this approach can also be extended to treat the flexibility of protein loops.
Conclusions and Future Directions
Biomolecular recognition can be described as a balanced interplay of different forces and energetic contributions. The long-range electrostatic forces together with the short-range van der Waals interactions, shape complementarity, hydrogen bonding, and hydrophobic effects determine the interactions of associating molecules. The flexibility of the partners on their binding is important for induced fit and makes an entropic contribution to the recognition process. Modeling of the structural, dynamic, and energetic determinants provides a tool to simulate the interactions of the macromolecules on their complexation. Different computational docking programs model the forces and the energetic contributions differently. Some docking programs mimic the diffusional association of the molecules; others base their approach mostly on the shape complementarity of associating partners. The varying degrees of the incorporation of electrostatic and hydrophobic interactions and the structural plasticity of the molecules on binding influences the accuracy of the prediction of the structure of the bound complex and the ability to compute kinetic and thermodynamic parameters. Because of the large number of degrees of freedom of biological molecules in solution, the problem of sampling and scoring of the docked solutions is very challenging. The computational methods must aim at simple, computationally feasible models that provide reasonable accuracy and help to answer the question of how biomolecules recognize and bind with their partners selectively and specifically. Current protein-protein docking algorithms can provide good predictions of the structures of complexes when the conformational changes on binding are very limited, but they usually fail when large conformational changes occur (89, 90); see also the CAPRI experiment for the comparative evaluation of protein-protein docking for structure prediction (http://capri.ebi.ac.uk). Ongoing improvements of the computational models for biomolecular interactions include the treatment of large-scale conformational changes of the macromolecules on binding and the modeling of solvation and polarization effects, among others.
References
1. Suckling CJ. Molecular recognition—A universal molecular science? Cell. Mol. Life Sci. 1991; 47:1093-1095.
2. Noller HF. Ribosomal RNA and translation. Annu. Rev. Biochem. 1991; 60:191-227.
3. Guthrie C. Messenger RNA splicing in yeast: clues to why the spliceosome is a ribonucleoprotein. Science 1991; 253:157-163.
4. Uetz P, Giot L, Cagney G, Mansfield TA, Judson RS, Knight JR, Lockshon D, Narayan V, Srinivasan M, Pochart P, Qureshi-Emili, Li Y, Godwin B, Conover D, Kalbfleisch T, Vijayadamodar G, Yang M, Johnston M, Fields S, Rothberg JM. A comprehensive analysis of protein-protein interactions in Saccharomyces cerevisiae. Nature 2000; 403:623-627.
5. Ito T, Chiba T, Ozawa R, Yoshida M, Hattori M, Sakaki Y. A comprehensive two-hybrid analysis to explore the yeast protein interactome. Proc. Natl. Acad. Sci. U.S.A. 2001; 98:4569-4574.
6. Cooper MA. Label-free screening of bio-molecular interactions. Anal. Bioanal. Chem. 2354; 377:834-842.
7. Yang Y, Wang H, Erie DA. Quantitative characterization of biomolecular assemblies and interactions using atomic force microscopy. Methods 2354; 29:175-187.
8. Tong AH, Evangelista M, Parsons AB, Xu H, Bader GD, Page N, Robinson M, Raghibizadeh S, Hogue CW, Bussey H, Andrews B, Tyers M, Boone C. Systematic genetic analysis with ordered arrays of yeast deletion mutants. Science 2001; 294:2364-2368.
9. Baumeister W, Grimm R, Walz J. Electron tomography of molecules and cells. Trends Cell Biol. 1999; 9:81-85.
10. Velazquez Campoy A, Freire E. ITC in the post-genomic era...? Priceless. Biophys. Chem. 2005; 115:115-124.
11. Wade RC, Gabdoulline RR, Liidemann SK, Lounnas V. Electrostatic steering and ionic tethering in enzyme-ligand binding: insights from simulations. Proc. Natl. Acad. Sci. U.S.A. 1998; 95:5942-5949.
12. Ma B, Kumar S, Tsai CJ, Nussinov R. Folding funnels and binding mechanisms. Protein Eng. 1999; 12:713-720.
13. Koshland D. The key-lock theory and the induced fit theory. Angew. Chem. Int. Ed. Engl. 1994; 33:2375-2378.
14. Jorgensen WL. Rusting of the lock and key model for proteinligand binding. Science 1991; 254:954-955.
15. Brooks CL III, Karplus M, Pettitt BM. Proteins. A Theoretical Perspective of Dynamics, Structure, and Thermodynamics. 1988. Wiley, New York.
16. Betts MJ, Sternberg MJ. An analysis of conformational changes on protein-protein association: implications for predictive docking. Protein Eng. 1999; 12:271-283.
17. Najmanovich R, Kuttner J, Sobolev V, Edelman M. Side chain flexibility in proteins upon ligand binding. Proteins 2000; 39:261-268.
18. Keskin O, Ma B, Nussinov R. Hot regions in protein-protein interactions: the organization and contribution of structurally conserved hot spot residues. J. Mol. Biol. 2005; 345:1281-1294.
19. Kimura SR, Brower RC, Vajda S, Camacho CJ. Dynamical view of the positions of key side chains in protein-protein recognition. Biophys. J. 2001; 80:635-642.
20. Rajamani D, Thiel S, Vajda S, Camacho CJ. Anchor residues in protein-protein interactions. Proc. Natl. Acad. Sci. U.S.A. 2004; 101:11287-11292.
21. Arold S, O’Brien R, Franken P, Strub MP, Hoh F, Dumas C, Ladbury JE. RT loop flexibility enhances the specificity of Src family SH3 domains for HIV-1 Nef. Biochemistry 1998; 37:14683-14691.
22. Inga A, Monti P, Fronza G, Darden T, Resnick MA. p53 mutants exhbiting enhanced transcriptional activation and altered promoter selectivity are revealed using a sensitive, yeast-based functional assay. Oncogene 2001; 20:501-513.
23. Zomot E, Kanner BI. The interaction of the gamma-aminobutyric acid transporter GAT-1 with the neurotransmitter is selectively impaired by sulfhydryl modification of a conformationally sensitive cysteine residue engineered into extracellular loop IV. J. Biol. Chem. 2354; 278:42950-42958.
24. Ehrlich LP, Nilges M, Wade RC. The impact of protein flexibility on protein-protein docking. Proteins 2005; 58:126-133.
25. Chen R, Mintseris J, Janin J, Weng Z. A protein-protein docking benchmark. Proteins 2354; 52:88-91.
26. Vajda S, Camacho CJ. Protein-protein docking: is the glass half-full or half-empty? Trends Biotechnol. 2004; 22:110-116.
27. Derreumaux P, Schlick T. The loop opening/closing motion of the enzyme triosephosphate isomerase. Biophys. J. 1998; 74:72-81.
28. Gerstein M, Chothia C. Analysis of protein loop closure. Two types of hinges produce one motion in lactate dehydrogenase. J. Mol. Biol. 1991; 220:133-149.
29. Fitzgerald MM, Musah RA, McRee DE, Goodin DB. A ligandgated, hinged loop rearrangement opens a channel to a buried artificial protein cavity. Nat. Struct. Biol. 1996; 3:626-631.
30. Gerstein M, Lesk AM, Chothia C. Structural mechanisms for domain movements in proteins. Biochemistry 1994; 33:6739-6749.
31. Hubbard SJ, Argos P. Cavities and packing at protein interfaces. Protein Sci. 1994; 3:2194-2206.
32. Lennard-Jones JE. On the determination of molecular fields. ii. from the equation of state of a gas. Proc.R. Soc. London, Ser. A. 1924; 106:463.
33. Lennard-Jones JE. Cohesion. Proc. Phys. Soc. 1931; 43:461-482.
34. Slater JC, Kirkwood JG. The Van Der Waals Forces in Gases. Phys Rev. 1931; 37:682-686.
35. Schlick T. Molecular Modeling and Simulation: An Interdicsiplinary Guide. 2002. Springer, New York.
36. Fogolari F, Brigo A, Molinari H. The Poisson-Boltzmann equation for biomolecular electrostatics: a tool for structural biology. J. Mol. Recognit. 2002; 15:377-392.
37. Bashford D. Macroscopic electrostatic models for protonation states in proteins. Front. Biosci. 2004; 9:1082-1099.
38. Baker NA. Poisson-Boltzmann methods for biomolecular electrostatics. Methods Enzymol. 2004; 383:94-118.
39. Wang T, Tomic S, Gabdoulline RR, Wade RC. How optimal are the binding energetics of barnase and barstar? Biophys. J. 2004; 87:1618-1630.
40. Dong F, Vijayakumar M, Zhou HX. Comparison of calculation and experiment implicates significant electrostatic contributions to the binding stability of barnase and barstar. Biophys. J. 2354; 85:49-60.
41. Daune M. Molecular Biophysics: Structures in Motion. 1999. Oxford, University Press.
42. Boobbyer DN, Goodford PJ, McWhinnie PM, Wade RC. New hydrogen-bond potentials for use in determining energetically favorable binding sites on molecules of known structure. J. Med. Chem. 1989; 32:1083-1094.
43. Fischer S, Verma CS. Binding of buried structural water increases the flexibility of proteins. Proc. Natl. Acad. Sci. U.S.A. 1999; 96:9613-9615.
44. Dill KA. Dominant forces in protein folding. Biochemistry 1990; 29:7133-7155.
45. Walls PH, Sternberg MJ. New algorithm to model protein-protein recognition based on surface complementarity. Applications to antibody-antigen docking. J. Mol. Biol. 1992; 228:277-297.
46. Shanbhag VP. Estimation of surface hydrophobicity of proteins by partitioning. Methods Enzymol. 1994; 228:254-264.
47. Korn AP, Burnett RM. Distribution and complementarity of hydropathy in multisubunit proteins. Proteins 1991; 9:37-55.
48. Vakser IA, Aflalo C. Hydrophobic docking: a proposed enhancement to molecular recognition techniques. Proteins 1994; 20:320- 329.
49. Berchanski A, Shapira B, Eisenstein M. Hydrophobic complementarity in protein-protein docking. Proteins 2004; 56:130-142.
50. Eisenberg D, Wilcox W, McLachlan AD. Hydrophobicity and amphiphilicity in protein structure. J. Cell. Biochem. 1986; 31:11-17.
51. Lee B, Richards FM. The interpretation of protein structures: estimation of static accessibility. J. Mol. Biol. 1971; 55:379-400.
52. Shrake A, Rupley JA. Environment and exposure to solvent of protein atoms. Lysozyme and insulin. J. Mol. Biol. 1973; 79:351-371.
53. Murphy KP, Xie D, Thompson KS, Amzel LM, Freire E. Entropy in biological binding processes: estimation of translational entropy loss. Proteins 1994; 18:63-67.
54. Gilson MK, Zhou HX. Calculation of protein-ligand binding affinities. Annu. Rev. Biophys. Biomol. Struct. 2007; 36:21-42.
55. Janin J. Quantifying biological specificity: the statistical mechanics of molecular recognition. Proteins 1996; 25:438-445.
56. Brady GP, Sharp KA. Entropy in protein folding and in protein- protein interactions. Curr. Opin. Struct. Biol. 1997; 7:215-221.
57. Stone MJ. NMR relaxation studies of the role of conformational entropy in protein stability and ligand binding. Acc. Chem. Res. 2001; 34:379-388.
58. Jackson RM, Sternberg MJ. A continuum model for protein-protein interactions: application to the docking problem. J. Mol. Biol. 1995; 250:258-275.
59. Weng Z, Vajda S, Delisi C. Prediction of protein complexes using empirical free energy functions. Protein Sci. 1996; 5:614-626.
60. Sharp KA, Friedman RA, Misra V, Hecht J, Honig B. Salt effects on polyelectrolyte-ligand binding: comparison of Poisson- Boltzmann, and limiting law/counterion binding models. Biopolymers 1995; 36:245-262.
61. Dunitz JD. The Entropic Cost of Bound Water in Crystals and Biomolecules. Science 1994; 264:670.
62. Madura JD, Briggs JM, Wade RC, Gabdoulline RR. Brownian dynamics. In: Encyclopedia of Computational Chemistry. Schleyer PvR, Allinger NL, Clark T, Gasteiger J, Kollman PA, Schaefer III HF and Schreiner PR, eds. 1998. John Wiley & Sons, Chichester, UK.
63. Gabdoulline RR, Wade RC. Biomolecular diffusional association. Curr. Opin. Struct. Biol. 2002; 12:204-213.
64. Ermak DL, McCammon JA. Brownian dynamics with hydrodynamic interactions. J. Chem. Phys. 1978; 69:1352-1360.
65. Northrup SH, Allison SA, McCammon JA. Brownian dynamics simulation of diffusion-influenced biomolecular reactions. J. Chem. Phys. 1984; 80:1517-1524.
66. Madura JD, Briggs JM, Wade RC, Davis ME, Luty BA, Ilin A, Antosiewicz J. Electrostatics and diffusion of molecules in solution: simulations with the university of Houston brownian dynamics program. Comput. Phys. Commun. 1995; 91:57-95.
67. Gabdoulline RR, Wade RC. Brownian dynamics simulation of protein-protein diffusional encounter. Methods 1998; 14:329-341.
68. Castro G, Boswell CA, Northrup SH. Dynamics of protein-protein docking: cytochrome c and cytochrome c peroxidase revisited. J. Biomol. Struct. Dyn. 1998; 16:413-424.
69. Verlet L. Computer “Experiments” on Classical Fluid. I. Thermodynamical Properties of Lennard-Jones Molecules. Phys. Rev. 1967; 159:98-103.
70. Verlet L. Computer “Experiments” on classical fluids. II. Equilibrium correlation functions. Phys. Rev. 1968; 165:201-214.
71. Ewald PP. Die Berchnung optischer und elektrostatischer Gitter- potentiale. Ann. Phys. 1921; 64:253-287.
72. Petersen HG. Accuracy and efficiency of the particle mesh Ewald method. J. Chem. Phys. 1995; 103:3668-3679.
73. Cherfils J, Duquerroy S, Janin J. Protein-protein recognition analyzed by docking simulation. Proteins 1991; 11:271-280.
74. Zacharias M. Protein-protein docking with a reduced protein model accounting for side chain flexibility. Protein Sci. 2354; 12:1271-1282.
75. Marrink SJ, Risselada HJ, Yefimov S, Tieleman DP, de Vries AH. The MARTINI force field: coarse grained model for biomolecular simulations. J. Phys. Chem. B. 2007; 111:7812-7824.
76. Kurcinski M, Kolinski A. Hierarchical modeling of protein interactions. J. Mol. Model. 2007; 13:691-698.
77. Motiejunas D, Gabdoulline RR, Wang T, Feldman-Salit A, Johann T, Winn PJ, Wade RC. Protein-protein docking by simulating the process of association subject to biochemical constraints. Proteins. In Press.
78. Goodsell DS, Olson AJ. Automated docking of substrates to proteins by simulated annealing. Proteins 1990; 8:195-202.
79. Jones G, Willett P, Glen RC, Leach AR, Taylor R. Development and validation of a genetic algorithm for flexible docking. J. Mol. Biol. 1997; 267:727-748.
80. Korb O, Stu tzle T, Exner TE. 2006. PLANTS: application of ant colony optimization to structure-based drug design. In Proc. Ant Colony Optimization and Swarm Intelligence, 5th International Workshop, ANTS 2006 LNCS 4150. pp. 247-258.
81. Gardiner EJ, Willett P, Artymiuk PJ. Protein docking using a genetic algorithm. Proteins 2001; 44:44-56.
82. Poirrette AR, Artymiuk PJ, Rice DW, Willett P. Comparison of protein surfaces using a genetic algorithm. J. Comput. Aided Mol. Des. 1997; 11:557-569.
83. Katchalski-Katzir E, Shariv I, Eisenstein M, Friesem AA, Aflalo C, Vakser IA. Molecular surface recognition: determination of geometric fit between proteins and their ligands by correlation techniques. Proc. Natl. Acad. Sci. U.S.A. 1992; 89:2195-2199.
84. Mandell JG, Roberts VA, Pique ME, Kotlovyi V, Mitchell JC, Nelson E, Tsigelny I, Ten Eyck LF. Protein docking using continuum electrostatics and geometric fit. Protein Eng. 2001; 14:105-113.
85. Gray JJ, Moughon S, Wang C, Schueler-Furman O, Kuhlman B, Rohl CA, Baker D. Protein-protein docking with simultaneous optimization of rigid-body displacement and side chain conformations. J. Mol. Biol. 2354; 331:281-299.
86. Dunbrack Jr RL, Cohen FE. Bayesian statistical analysis of protein side chain rotamer preferences. Protein Sci. 1997; 6:1661-1681.
87. Wang C, Schueler-Furman O, Baker D. Improved side chain modeling for protein-protein docking. Protein Sci. 2005; 14:1328-1339.
88. Lorber DM, Udo MK, Shoichet BK. Protein-protein docking with multiple residue conformations and residue substitutions. Protein Sci. 2002; 11:1393-1408.
89. Janin J, Rodier F, Chakrabarti P, Bahadur RP. Macromolecular recognition in the Protein Data Bank. Acta Crystallogr. D Biol. Crystallogr. 2007; 63:1-8.
90. Gray JJ. High-resolution protein-protein docking. Curr. Opin. Struct. Biol. 2006; 16:183-193.
Further Reading
Cruciani G. Molecular interaction fields. In: Applications in Drug Discovery and ADME Prediction. Mannhold R, Kubinyi H, Folker G, eds. 2005. Wiley-VCH, Weinheim, Germany.
Leach AR. Molecular Modelling: Principles and Applications. 2nd edition. 2001. Pearson Education Limited, Harlow, UK.
Triggle DJ, Taylor JB. Comprehensive Medicinal Chemistry II. Volume 4. 2007. Elsevier, Oxford, UK.
See Also
Computational Chemistry in Biology
Non-covalent Interactions in Molecular Recognition
Protein-nucleic Acid Interactions
Protein-protein Interactions
Receptor-ligand Interactions in Biological Systems