Chemistry Essentials for Dummies
Chapter 4. Nuclear Chemistry
Half-Lives and Radioactive Dating
If you could watch a single atom of a radioactive isotope, U-238, for example, you wouldn’t be able to predict when that particular atom might decay. It may take a millisecond, or it may take a century. There’s simply no way to tell.
But if you have a large enough sample — what mathematicians call a statistically significant sample size — a pattern begins to emerge. It takes a certain amount of time for half the atoms in a sample to decay. It then takes the same amount of time for half the remaining radioactive atoms to decay, and the same amount of time for half of those remaining radioactive atoms to decay, and so on. The amount of time it takes for one-half of a sample to decay is called the half-life of the isotope, and it’s given the symbol t1/2. Table 4-1 shows this process.
Table 4-1. Half-Life Decay of a Radioactive Isotope
|
Number of Half-Lives |
Percent of the Radioactive Isotope Remaining |
|
0 |
100.00 |
|
1 |
50.00 |
|
2 |
25.00 |
|
3 |
12.50 |
|
4 |
6.25 |
|
5 |
3.13 |
|
6 |
1.56 |
|
7 |
0.78 |
|
8 |
0.39 |
|
9 |
0.20 |
|
10 |
0.10 |
Calculating remaining radioactivity
WARNING! The half-life decay of radioactive isotopes is not linear. For example, you can’t find the remaining amount of an isotope at 7.5 half-lives by finding the midpoint between 7 and 8 half-lives.
If you want to find times or amounts that are not associated with a simple multiple of a half-life, you can use this equation:
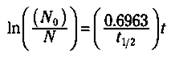
In the equation, ln stands for the natural logarithm (the base e log, not the base 10 log; it’s that In button on your calculator, not the log button). No is the amount of radioactive isotope that you start with (in grams, as a percentage, in the number of atoms, and so on), N is the amount of radioisotope left at some time (t), and t1/2 is the half-life of the radioisotope. If you know the half-life and the amount of the radioactive isotope that you start with, you can use this equation to calculate the amount remaining radioactive at any time.
Radioactive dating
A useful application of half-lives is radioactive dating. Carbon-14 (C-14), a radioactive isotope of carbon, is produced in the upper atmosphere by cosmic radiation. The primary carbon- containing compound in the atmosphere is carbon dioxide, and a very small amount of carbon dioxide contains C-14. Plants absorb C-14 during photosynthesis, so C-14 is incorporated into the cellular structure of plants. Plants are then eaten by animals, making C-14 a part of the cellular structure of all living things.
As long as an organism is alive, the amount of C-14 in its cellular structure remains constant. But when the organism dies, the amount of C-14 begins to decrease. Scientists know the half-life of C-14 (5,730 years), so they can figure out how long ago the organism died.
Radioactive dating using C-14 has been used to determine the age of skeletons found at archeological sites. It was also used to date the Shroud of Turin, a piece of linen in the shape of a burial cloth that contains an image of a man. Many thought that it was the burial cloth of Jesus, but in 1988, radiocarbon dating determined that the cloth dated from around 1200-1300 CE.
Carbon-14 dating can only determine the age of something that was once alive. It can’t determine the age of a moon rock or a meteorite. For nonliving substances, scientists use other isotopes, such as potassium-40.