Liquid-State Physical Chemistry: Fundamentals, Modeling, and Applications (2013)

8.4. Significant Liquid Structures*

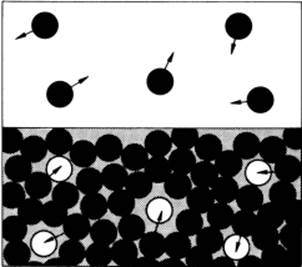
In the approach, which was advocated by Eyring and denoted by him as significant liquid structure theory⁶⁾ (here labeled as SLS theory), it is argued that a liquid behaves in many cases as an intermediate between a gas and a solid. From the fact that a simple liquid like Ar expands ∼12% upon melting and the associated large increase in fluidity, it can be concluded that the coordination number decreases, while simultaneously introducing some free volume in the liquid. Since XRD measurement have indicated that the intermolecular distances in the liquid are essentially the same as in the solid, the resulting structure is assumed to show some heterogeneity, containing a fraction of solid-like molecules and another fraction of holes. Holes of molecular size are favored because smaller holes cannot provide easy access to the entering molecules, which limits the increase of entropy. In contrast, larger holes will require excessive energy without a compensating increase in entropy. These holes change by one or more degrees of freedom for a molecule surrounding the hole from vibration to translation, and these molecules thus act like vapor molecules. Hence, the concept does not imply that a liquid is a mixture of a solid and a gas. Rather, a molecule has solid-like properties for the time it vibrates around an equilibrium position, but transforms instantaneously to a gas-like behavior for one or more degrees of freedom if it jumps into a neighboring hole. A simple schematic of this is process shown in Figure 8.5.

Figure 8.5 A schematic illustrating a liquid formed by removing at random molecules from a (glassy) solid. The holes so created mirror the molecules in the gas phase.

According to the law of rectilinear diameters (see Chapter 4), the average density of a liquid and its associated equilibrium vapor pressure is a linear function of temperature (roughly equal to ∼½ρ_solid at T_mp to ∼⅓ρ_solid at T_cri). A small decrease in temperature is expected due to thermal expansion, but this law indicates that the number density of molecules in the gas phase is about equal to the number density of vacancies in the liquid. In a simple nearest-neighbor model, the energy of vaporization per molecule is approximately ½zϕ, where z is the coordination number and ϕ is the bond energy. In a similar way it requires energy zϕ to create a hole in the liquid. The molecule removed from the interior of the liquid to the vapor can be added to the surface of the liquid, thereby regaining the energy ½zϕ, so leaving a hole costs only the energy of vaporization. Hence, a vacancy is expected to move as freely as a molecule in the gas phase and to have about the same energy and entropy, thus explaining the law of rectilinear diameters.

So, the thermodynamic behavior in this model is described by varying the fraction of gas-like and solid-like volume elements, while the overall thermodynamic behavior is given by the sum of the contributions of these elements. In the simplest form for gas-like regions the ideal gas model is used, whereas for solid-like elements the Einstein model (see Sections 5.3 and 6.1) is used. The crux is, obviously, to determine the fractions of gas-like and solid-like regions.

Since the holes are on average of molecular size, in one mole of liquid (V − V_s)/V_s moles of holes are present, where V and V_s are the molar volumes of the liquid and solid, respectively. Assuming complete randomness, the fraction of neighboring positions filled with molecules to with a hole is V_s/V. It thus follows that for N molecules there are

(8.60)

gas-like molecules and a remainder of N_s ≡ NV_s/V solid-like molecules. According to this model, the heat capacity C_V of a mole of, say Ar, is given by sum of the contributions of the V_s/V moles of solid and (V − V_s)/V moles of gas. Therefore

(8.61)

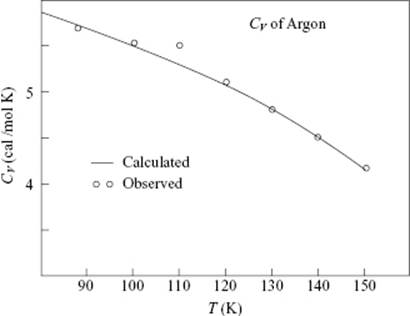
for which the good agreement with experiment is shown in Figure 8.6.

Figure 8.6 The experimental heat capacity C_V for liquid argon (circles) and the prediction according to Eq. (8.61) (solid line) using C_V,solid = 3R = 25.0 J mol⁻¹ K⁻¹ or 6.0 cal mol⁻¹ K⁻¹ and C_V,gas = 3R/2 = 12.5 J mol⁻¹ K⁻¹ or 3.0 cal mol⁻¹ K⁻¹.

Using the above concepts, the partition function Z_N can be written as

(8.62)

where Z_s and Z_g represent the partition functions of the solid-like and gas-like molecules, respectively.

For calculating Z_s we consider that holes surrounding a solid-like molecule introduce positional degeneracy. The number of additional accessible sites for a solid-like molecule is the number of holes around that molecule multiplied by the probability that this molecule has the required energy ε_h to be able to jump to these holes. The number of holes n_h is proportional to the excess volume and given by

(8.63)

with n as proportionality factor. The energy ε_h should be inversely proportional to the excess volume and directly proportional to the energy of sublimation E_s. Therefore

(8.64)

with a as proportionality factor. Since the parameter ε_h → ∞ for V → V_s and ε_h → 0 for V → ∞, this introduces cooperative behavior in theory. The total number of positions available, that is, original plus additional, to the solid-like molecule becomes

(8.65)

and Z_s becomes (using as the partition function for the pure solid-like molecule)

(8.66)

As noted, for the simplest choice is the Einstein model, for which the partition function using θ as the Einstein temperature, reads

(8.67)

The factor exp(−ϕ/2kT) takes into account that in a simple nearest-neighbor model −ϕ/2 is the potential energy of the solid-like, vibrating molecule and we interpret E_s ≡ −½(ϕ + 3kθ) as the sublimation energy. For Z_g we use straightforwardly the ideal gas expression with excess volume V − V_s and thermal wavelength Λ = (h²/2πmkT)^½, that is,

(8.68)

Hence, according to Eq. (8.62) we have for the partition function Z_N of the liquid

(8.69)

While the parameters E_s, θ and V_s have to be taken from solid-state data, either theoretical or experimental, the parameters a and n can be evaluated theoretically.

To calculate n, we use the molar volume V_mp at the melting point T_mp and consider that, close to T_mp and using the lattice coordination number z, n_h is given by

(8.70)

Comparison with Eq. (8.63) yields

(8.71)

To calculate a, we consider that a solid-like molecule has a kinetic energy 3kT/2. If a molecule is to pre-empt a neighboring position in addition to its original position, it must have additional kinetic energy equal to or in excess of that which the other (n − 1) neighboring molecules would otherwise introduce into this hole. If the average molecule divides its time equally between two neighboring sites, its energy density will be halved. As the molecule will be moving for (1/z)th of its time in the direction of any neighbor, the average kinetic energy of the (n − 1) ordinary molecules will provide a hole with kinetic energy ½(3kT/2)(n − 1)/z. This is also the value that ε_h = aE_sV_s/(V − V_s) must have at the melting temperature T_mp, that is,

(8.72)

Since at T_mp it holds that T_mpS_mp = E_mp, and the entropy of melting per molecule S_mp for a simple liquid is about 3k/2, we obtain E_mp = 3kT_mp/2 for the energy of melting E_mp. Moreover, since during melting holes are introduced in the solid, essentially accompanied by a potential energy change only, we also have

(8.73)

(8.74)

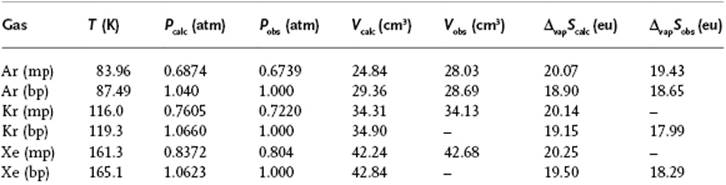
Equations (8.71) and (8.74) result in a = 0.00537 and n = 10.7 for Ar, using z = 12 and the data given in Table 8.3. The best empirical fit [21] yields a = 0.00534 and n = 10.8, so that there is good agreement. Some further data for Ar, Kr and Xe shown in Table 8.3 also demonstrate a good agreement with experimental data.

Table 8.3 Vapor pressure P, molar volume V and entropy of vaporization Δ_vapS for the noble gases Ar, Kr and Xe, and the parameters used.

Using the same parameters as for the LJD theory, the triple point for Ar is predicted to be 0.711ε/k, compared with 0.701ε/k according to LJD theory (Table 8.1). Predictions for V, U and S of Ar according to SLS and LJD theory are also shown in Table 8.1. The critical constants predicted are (LJD data in brackets)

to be compared with the “best” experimental corresponding states estimates⁷⁾

Overall, we conclude that for describing liquids SLS theory is better than LJD theory, which resembles more a superheated solid than a liquid.

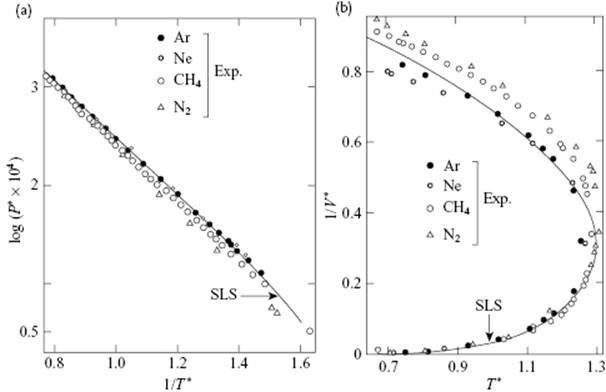
Some other predictions of SLS theory, which also show good agreement with experimental data, are given in Figure 8.7. For molecules that rotate freely in the liquid phase, such as CH₄ and N₂, Figure 8.7 shows the good agreement with experimental data. However, for those molecules that do not rotate freely in the liquid phase, such as Cl₂, some changes in Z_s must be made, for example, treating the rotation in the solid-like part as a vibration. In that case, a good agreement with experimental data was also reached. For example, for the temperature range of 180 K to 240 K the heat capacity at constant pressure C_P, as a calculated from C_P = C_V − TVα²β with C_V the heat capacity at constant volume, α = (1/V)(∂V/∂T)_P the expansivity and β = −(1/V)(∂V/∂P)_T the compressibility, all calculated from Z_N, differ by only ∼2% from the experimental values. The method has been applied to molten metals, molten salts and quantum liquids such as H₂ and Ne, with fairly good results. Application of the theory to many liquids and phenomena has been reviewed by Eyring and Jhon [23].

Figure 8.7 SLS theory results. (a) The logarithm of the reduced vapor pressure P* for simple liquids versus reciprocal reduced temperature 1/T*; (b) The reduced density versus 1/V* versus reduced temperature T* for SLS theory (T = (ε/k)T*, V = V*(N/σ³) and P = (ε/σ³)P*).

From the previous data and figures, it is concluded that quite acceptable agreement with experiment can be obtained. Nevertheless, the basis of SLS theory is not really clear and the approach has essentially been abandoned. Although the model has been rather successful in estimating thermodynamic properties, a basic feature of liquids – the pair correlation function – is largely absent. Although at a late stage of the development of this theory attempts were made [24] to introduce the pair correlation function, the procedure used must be characterized as artificial.

Problem 8.8

Show that the partition function of the significant liquid theory reduces to the ideal gas and solid-state partition functions if V → ∞ and V → 0, respectively.

Problem 8.9

Calculate the vapor pressure from significant liquid structures theory for atomic fluids using the ideal gas and Einstein partition functions for the gas-like and solid-like phases, respectively.

Problem 8.10

Is it possible to calculate the RDF for the significant liquid structures theory without further approximations of additions?