Liquid-State Physical Chemistry: Fundamentals, Modeling, and Applications (2013)

10.2. Towards a Microscopic Interpretation

So, an applied field E introduces into a material a polarization P = ε₀(ε_r − 1)E., and our task is now to interpret the polarization P in microscopic terms. In general, we have several molecular contributions to the polarization. First, if the molecules are polar and have a dipole moment³⁾ μ, we have the alignment of these permanent dipoles due to the applied field. This process results in a polarization contribution labeled P_μ. Second, even if we have nonpolar molecules, all molecules have an electronic polarizability⁴⁾ α_ele and molecular polarizability α_mol, collectively denoted by α, that results in a dipole moment induced by the applied field. This contribution is labeled P_α. The field experienced by the molecules is not equal to the applied field E as the surrounding molecules shield the reference molecule from the applied field, and a polar reference molecule will influence the surroundings leading to a different shielding than for a nonpolar molecule. If we have N molecules in a volume V, we may write P_μ = (N/V)p_μ and P_α = (N/V)p_α. Here, p_μ represents the (rotational) average dipole moment , which is dependent on the directional fieldE_dir experienced by the molecules. For p_α we have p_α = αE_int, where E_int is the internal field. Although both fields E_dir and E_int are proportional to the applied field E, they are not the same because a proportional increase in all three components of E will affect the magnitude of the induced dipole moment but not the directional effect for the permanent dipole. Hence, our task is to calculate E_int, E_dir and so that P_μ and P_α can be determined.

Altogether, in microscopic terms polarization can be interpreted as the number of molecules N with (effective) dipole moment μ_eff in a volume V, that is

(10.9)

Overall, the effective dipole moment is described by μ_eff = α_effE_loc, where α_eff is the effective polarizability of the molecule and E_loc is the local field, the latter being the appropriate combination of the internal and directional field. We deal first with gases and thereafter with liquids and solutions.

Problem 10.3

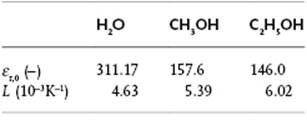
The relative permittivity ε_r can be accurately described by ε_r(T) = ε_r,0exp(−LT), with as parameters ε_r,0 and L. Calculate ε_r(298) for the three liquids indicated (see Table 10.1).

Table 10.1 Parameters ε_r,0 and L for H₂O, CH₃OH, and C₂H₅OH.