Liquid-State Physical Chemistry: Fundamentals, Modeling, and Applications (2013)

14.6. Neutral Molecules

In Chapter 11 we discussed regular solutions and obtained for the activity coefficients of apolar compounds

(14.53)

where w is the interaction parameter, z the coordination number, and x₁ and x₂ are the mole fractions. The conversion of activity coefficients for mole fractions γ_x to activity coefficients for molarities γ_c was also provided.

Using regular solution theory (see Chapter 11) the final result is

(14.54)

where V is the molar volume and x the mole fraction of the species, designated by the subscripts 1 and 2. This type of result can be plugged directly into the rate equations.

In solution, solvation effects can play a role, and the entropy of activation can help to study this effect. From the kinetic analysis it will be clear that in k_rea = A exp(−E_act/RT) for unimolecular reactions in solution the factor A = e(kT/h)exp(ΔS^‡/R), so that, if the specific reaction rate and energy of activation are known, it is possible to estimate the entropy of activation. For the reaction of triethylamine with ethyl bromide in mixtures of acetone and benzene, the data are given in Table 14.2. It can be seen that the entropy of activation remains almost constant over the range from 20 to 100% acetone in the mixture, implying that the activated state is solvated as long as the solvent contains at least one-fifth of acetone. In benzene, the activated state is probably hardly solvated, which leads to a lower entropy. The accompanying small decrease in activation energy is insufficient to compensate for the increase in entropy.

Table 14.2 Entropies and activation energies in acetone–benzene mixtures for the reaction between ethyl bromide and triethylamine.^a)

a) Data from Ref. [11].

For polar molecules, orientation effects will also play a role. Kirkwood [7] derived, on the basis of electrostatic considerations and neglecting short-range van der Waals interactions, the Gibbs energy of transferring a molecule with a strong dipole from a solvent with permittivity ε_r = 1 to a solvent with ε_r = ε_r. This quantity is related to the activity coefficient γ for which the dilute gas with ε_r = 1 is the standard state. The result is

(14.55)

with r the molecular radius.

For the reaction A + B → M^‡ → X + Y, the rate constant becomes

(14.56)

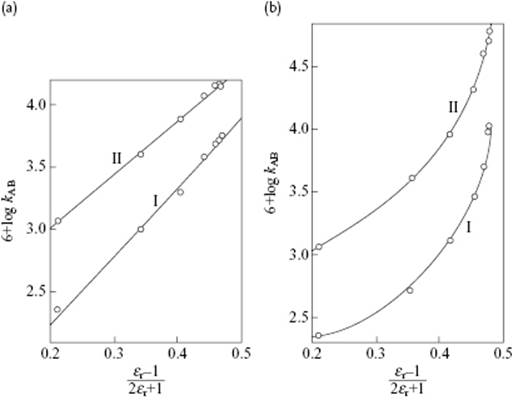
A plot of lnk_AB versus (ε_r − 1)/(2ε_r + 1) should yield a straight line for the same reaction carried in different solvents. Figure 14.4 shows an example of the specific rate constant for the reactions between pyridine and benzylbromide (I) and triethylamine and benzyl bromide (II) in alcohol–benzene mixtures (Figure 14.4a) and benzene–nitrobenzene mixtures (Figure 14.4b) as a function of (ε_r − 1)/(2ε_r + 1). The graph for the reactions in alcohol–benzene mixtures is almost linear, in agreement with theory, whereas the graph for the benzene–nitrobenzene mixtures showed considerable deviations. This implies that nonelectrostatic forces play a considerable role and must not be neglected.

Figure 14.4 Specific rate constants for the reactions between pyridine and benzylbromide (I) and triethylamine and benzyl bromide (II) in (a) alcohol–benzene mixtures and (b) benzene–nitrobenzene mixtures. Data from Ref. [11].

Problem 14.3

Discuss why, for reactions between triethylamine and benzyl bromide in benzene–nitrobenzene mixtures, deviations from a linear plot of lnk_AB versus (ε_r − 1)/(2ε_r + 1) are to be expected.