MCAT General Chemistry Review
Chapter 1: Atomic Structure
1.3 Rutherford, Planck, and Bohr
In 1910, Ernest Rutherford provided experimental evidence that an atom has a dense, positively charged nucleus that accounts for only a small portion of the atom’s volume. Eleven years earlier, Max Planck developed the first quantum theory, proposing that energy emitted as electromagnetic radiation from matter comes in discrete bundles called quanta. The energy of a quantum, he determined, is given by the Planck relation:
E = hf
Equation 1.1
where h is a proportionality constant known as Planck’s constant, equal to 6.626 × 10−34 J·s, and f (sometimes designated by the Greek letter nu, ν) is the frequency of the radiation.
BRIDGE
Recall from Chapter 8 of MCAT Physics Review that the speed of light (or any wave) can be calculated using v = fλ. The speed of light, c, is ![]() This equation can be incorporated into the equation for quantum energy to provide different derivations.
This equation can be incorporated into the equation for quantum energy to provide different derivations.
BOHR MODEL
In 1913, Danish physicist Niels Bohr used the work of Rutherford and Planck to develop his model of the electronic structure of the hydrogen atom. Starting from Rutherford’s findings, Bohr assumed that the hydrogen atom consisted of a central proton around which an electron traveled in a circular orbit. He postulated that the centripetal force acting on the electron as it revolved around the nucleus was created by the electrostatic force between the positively charged proton and the negatively charged electron.
Bohr used Planck’s quantum theory to correct certain assumptions that classical physics made about the pathways of electrons. Classical mechanics postulates that an object revolving in a circle, such as an electron, may assume an infinite number of values for its radius and velocity. The angular momentum (L = mvr) and kinetic energy 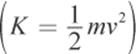 of the object could therefore take on any value. However, by incorporating Planck’s quantum theory into his model, Bohr placed restrictions on the possible values of the angular momentum. Bohr predicted that the possible values for the angular momentum of an electron orbiting a hydrogen nucleus could be given by:
of the object could therefore take on any value. However, by incorporating Planck’s quantum theory into his model, Bohr placed restrictions on the possible values of the angular momentum. Bohr predicted that the possible values for the angular momentum of an electron orbiting a hydrogen nucleus could be given by:
![]()
Equation 1.2
where n is the principal quantum number, which can be any positive integer, and h is Planck’s constant. Because the only variable is the principal quantum number, the angular momentum of an electron changes only in discrete amounts with respect to the principal quantum number. Note the similarities between quantized angular momentum and Planck’s concept of quantized energy.
MCAT EXPERTISE
When you see a formula in your review or on Test Day, focus on ratios and relationships. This simplifies our calculations to a conceptual understanding, which is usually enough to lead us to the right answer. Further, the MCAT tends to ask how changes in one variable may affect another variable, rather than a plug-and-chug application of complex equations.
Bohr then related the permitted angular momentum values to the energy of the electron to obtain:
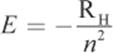
Equation 1.3
where RH is the experimentally determined Rydberg unit of energy, equal to ![]() Therefore, like angular momentum, the energy of the electron changes in discrete amounts with respect to the quantum number. A value of zero energy was assigned to the state in which the proton and electron are separated completely, meaning that there is no attractive force between them. Therefore, the electron in any of its quantized states in the atom will have an attractive force toward the proton; this is represented by the negative sign in Equation 1.3. Ultimately, the only thing the energy equation is saying is that the energy of an electron increases—becomes less negative—the farther out from the nucleus that it is located (increasing n). This is an important point: while the magnitude of the fraction is getting smaller, the actual value it represents is getting larger (becoming less negative).
Therefore, like angular momentum, the energy of the electron changes in discrete amounts with respect to the quantum number. A value of zero energy was assigned to the state in which the proton and electron are separated completely, meaning that there is no attractive force between them. Therefore, the electron in any of its quantized states in the atom will have an attractive force toward the proton; this is represented by the negative sign in Equation 1.3. Ultimately, the only thing the energy equation is saying is that the energy of an electron increases—becomes less negative—the farther out from the nucleus that it is located (increasing n). This is an important point: while the magnitude of the fraction is getting smaller, the actual value it represents is getting larger (becoming less negative).
KEY CONCEPT
At first glance, it may not be clear that the energy (E) is directly proportional to the principal quantum number (n) in Equation 1.3. Take notice of the negative sign, which causes the values to approach zero from a more negative value as n increases (thereby increasing the energy). Negative signs are as important as a variable’s location in a fraction when it comes to determining proportionality.
Think of the concept of quantized energy as being similar to the change in gravitational potential energy that you experience when you ascend or descend a flight of stairs. Unlike a ramp, on which you could take an infinite number of steps associated with a continuum of potential energy changes, a staircase only allows you certain changes in height and, as a result, allows only certain discrete (quantized) changes of potential energy.
Bohr came to describe the structure of the hydrogen atom as a nucleus with one proton forming a dense core, around which a single electron revolved in a defined pathway (orbit) at a discrete energy value. If one could transfer an amount of energy exactly equal to the difference between one orbit and another, this could result in the electron “jumping” from one orbit to a higher-energy one. These orbits had increasing radii, and the orbit with the smallest, lowest-energy radius was defined as the ground state (n = 1). More generally, the ground state of an atom is the state of lowest energy, in which all electrons are in the lowest possible orbitals. In Bohr’s model, the electron was promoted to an orbit with a larger radius (higher energy), the atom was said to be in the excited state. In general, an atom is in an excited state when at least one electron has moved to a subshell of higher than normal energy. Bohr likened his model of the hydrogen atom to the planets orbiting the sun, in which each planet traveled along a roughly circular pathway at set distances—and energy values—from the sun. Bohr’s Nobel Prize-winning model was reconsidered over the next two decades, but remains an important conceptualization of atomic behavior. In particular, remember that we now know that electrons are not restricted to specific pathways, but tend to be localized in certain regions of space.
MCAT EXPERTISE
Note that all systems tend toward minimal energy; thus on the MCAT, atoms of any element will generally exist in the ground state unless subjected to extremely high temperatures or irradiation.
APPLICATIONS OF THE BOHR MODEL
The Bohr model of the hydrogen atom (and other one-electron systems, such as He+ and Li2+) is useful for explaining the atomic emission and absorption spectra of atoms.
MNEMONIC
As electrons go from a lower energy level to a higher energy level, they get AHED:
· Absorb light
· Higher potential
· Excited
· Distant (from the nucleus)
Atomic Emission Spectra
At room temperature, the majority of atoms in a sample are in the ground state. However, electrons can be excited to higher energy levels by heat or other energy forms to yield excited states. Because the lifetime of an excited state is brief, the electrons will return rapidly to the ground state, resulting in the emission of discrete amounts of energy in the form of photons, as shown in Figure 1.5.
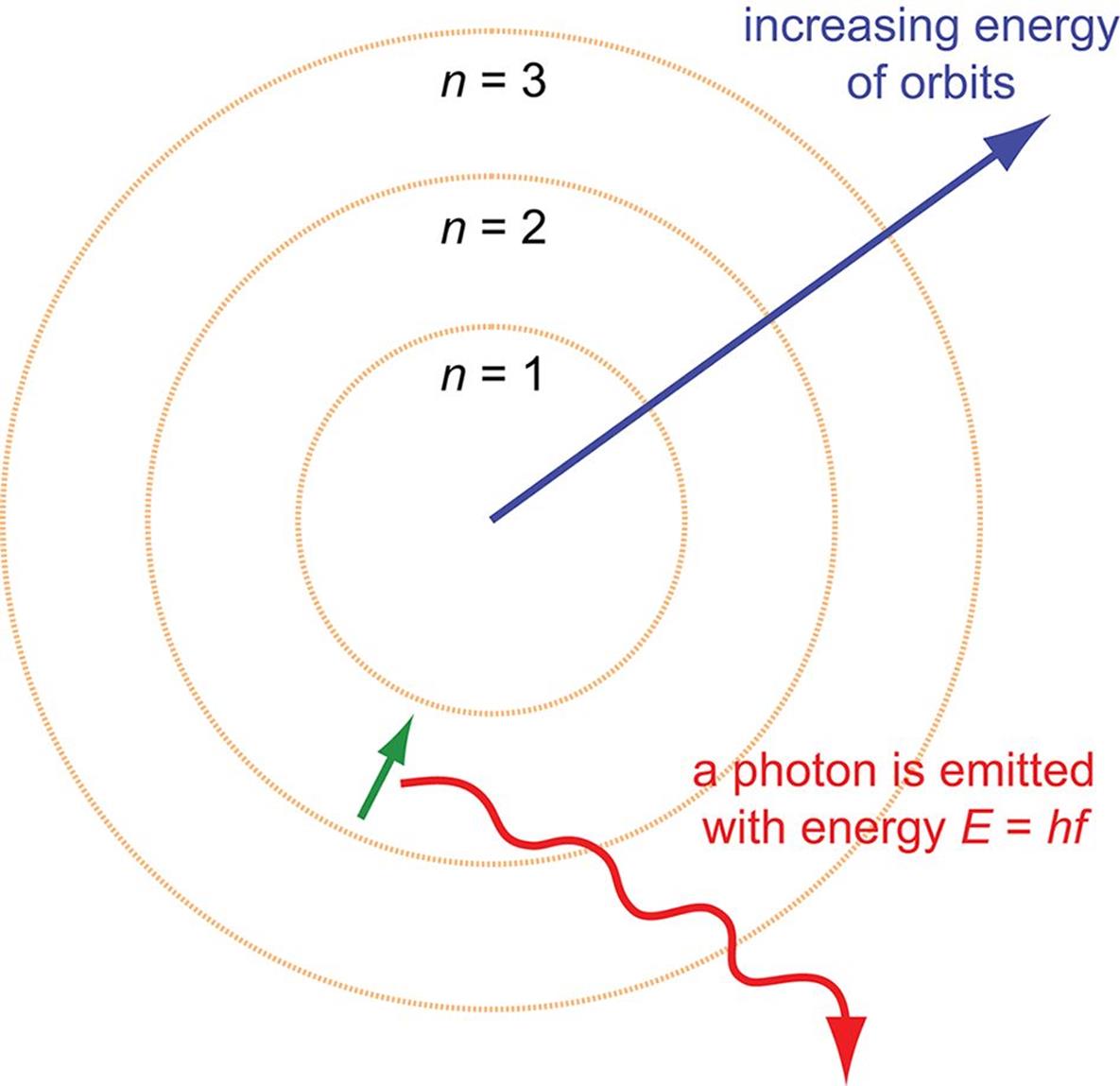 Figure 1.5. Atomic Emission of a Photon as a Result of a Ground State Transition
Figure 1.5. Atomic Emission of a Photon as a Result of a Ground State Transition
The electromagnetic energy of these photons can be determined using the following equation:
![]()
Equation 1.4
where h is Planck’s constant, c is the speed of light in a vacuum 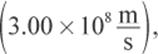 and λ is the wavelength of the radiation. Note that Equation 1.4 is just a combination of two other equations: E = hf and c = f λ.
and λ is the wavelength of the radiation. Note that Equation 1.4 is just a combination of two other equations: E = hf and c = f λ.
The electrons in an atom can be excited to different energy levels. When these electrons return to their ground states, each will emit a photon with a wavelength characteristic of the specific energy transition it undergoes. As described above, these energy transitions do not form a continuum, but rather are quantized to certain values. Thus, the spectrum is composed of light at specified frequencies. It is sometimes called a line spectrum, where each line on the emission spectrum corresponds to a specific electron transition. Because each element can have its electrons excited to a different set of distinct energy levels, each possesses a unique atomic emission spectrum, which can be used as a fingerprint for the element. One particular application of atomic emission spectroscopy is in the analysis of stars and planets: while a physical sample may be impossible to procure, the light from a star can be resolved into its component wavelengths, which are then matched to the known line spectra of the elements as shown in Figure 1.6.
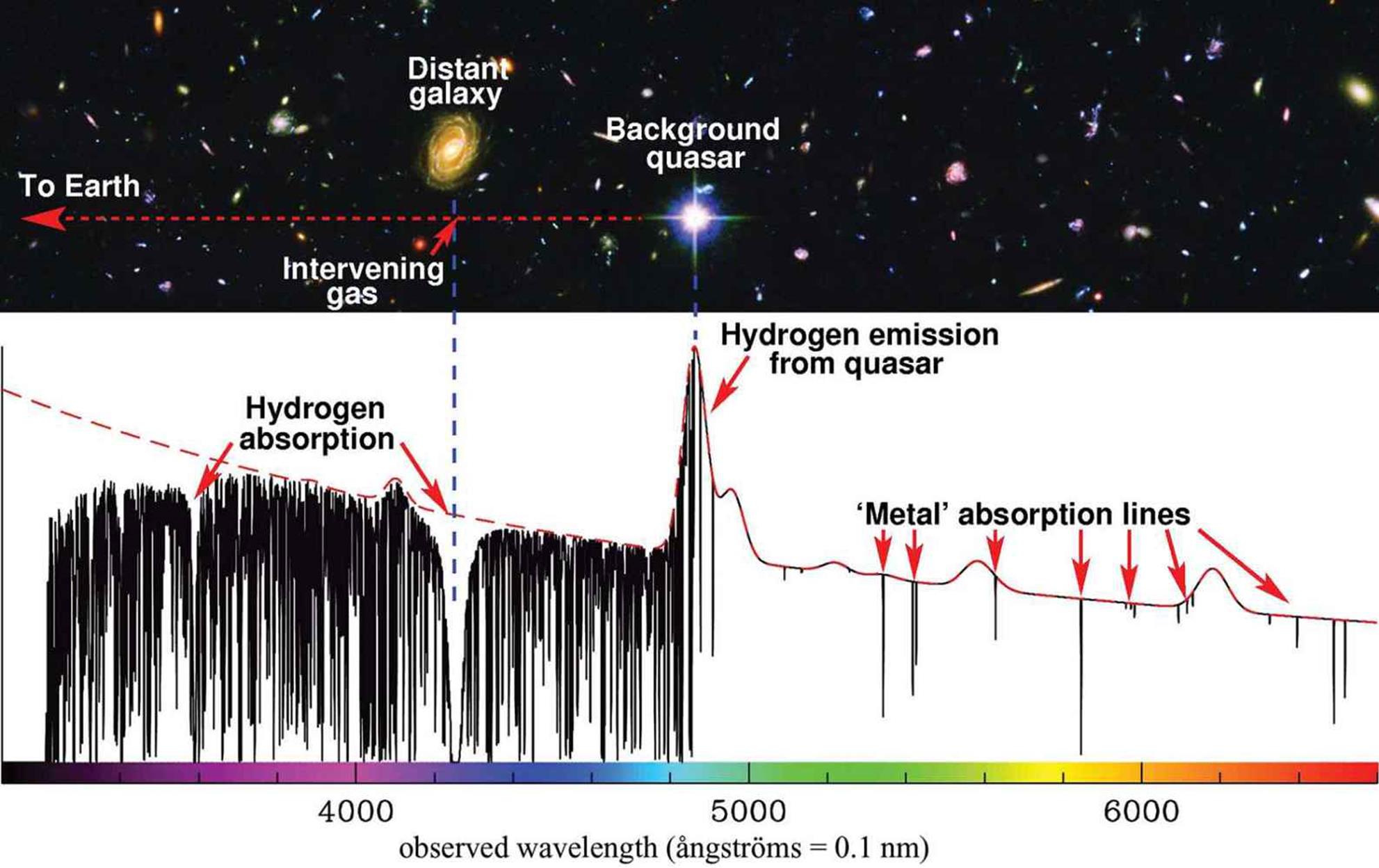 Figure 1.6. Line Spectrum with Transition Wavelengths for Various Celestial Bodies
Figure 1.6. Line Spectrum with Transition Wavelengths for Various Celestial Bodies
REAL WORLD
Emissions from electrons dropping from an excited state to a ground state give rise to fluorescence. What we see is the color of the emitted light.
The Bohr model of the hydrogen atom explained the atomic emission spectrum of hydrogen, which is the simplest emission spectrum among all the elements. The group of hydrogen emission lines corresponding to transitions from energy levels n ≥ 2 to n = 1 is known as the Lyman series. The group corresponding to transitions from energy levels n ≥ 3 to n = 2 is known as the Balmer series, and includes four wavelengths in the visible region. The Lyman series includes larger energy transitions than the Balmer series; it therefore has shorter photon wavelengths in the UV region of the electromagnetic spectrum. The Paschen series corresponds to transitions from n ≥ 4 to n = 3. These energy transition series can be seen in Figure 1.7.
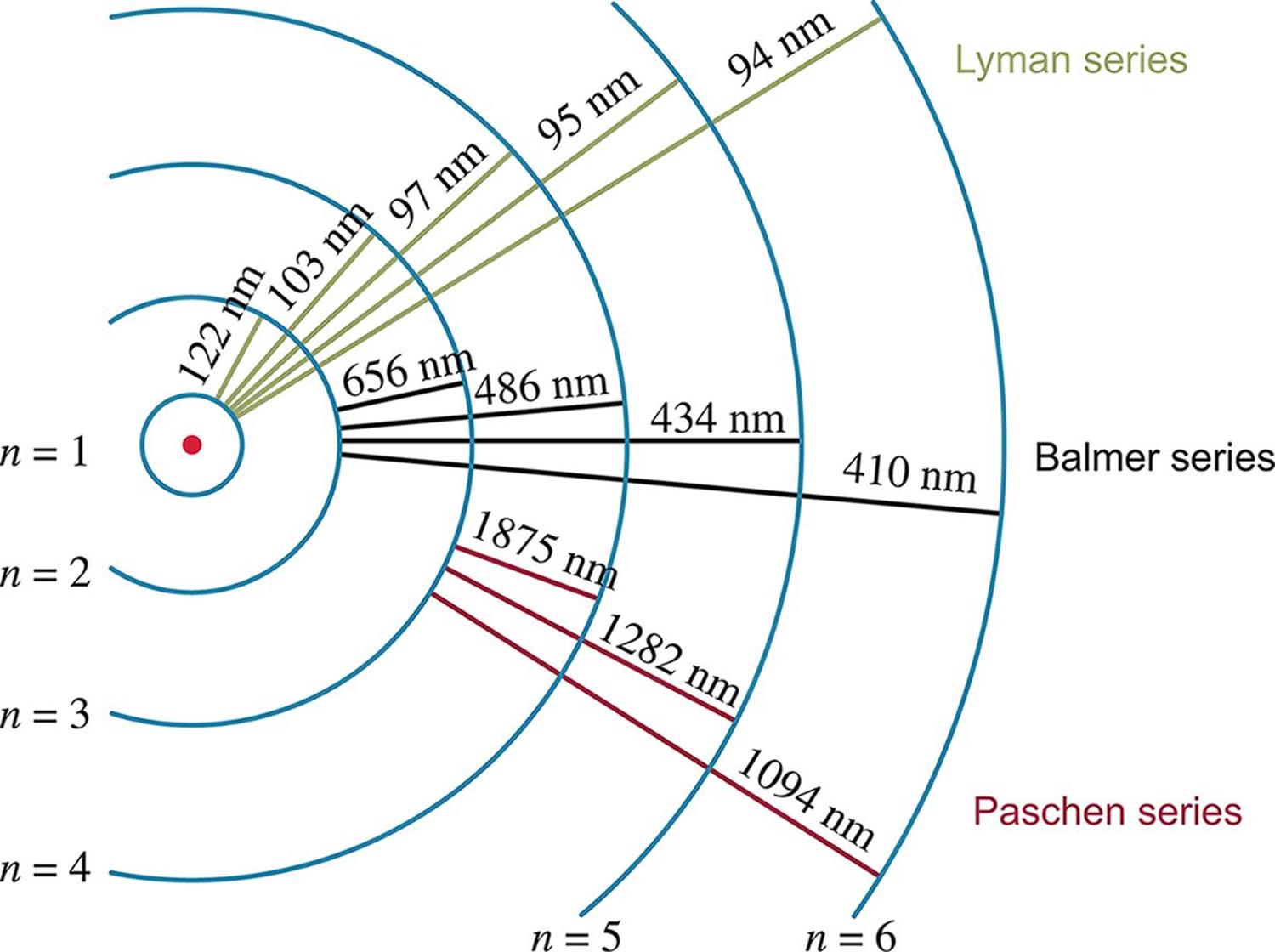 Figure 1.7. Wavelengths of Electron Orbital Transitions Energy is inversely proportional to wavelength:
Figure 1.7. Wavelengths of Electron Orbital Transitions Energy is inversely proportional to wavelength: ![]()
The energy associated with a change in the principal quantum number from a higher initial value ni to a lower final value nf is equal to the energy of the photon predicted by Planck’s quantum theory. Combining Bohr’s and Planck’s calculations, we can derive:
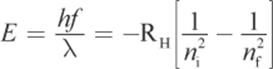
Equation 1.5
This complex-appearing equation essentially says: The energy of the emitted photon corresponds to the difference in energy between the higher-energy initial state and the lower-energy final state.
KEY CONCEPT
This equation is nothing new; it is simply derived from conservation of energy by setting the energy of a photon 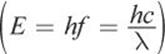 equal to the energy of the electron transition (from
equal to the energy of the electron transition (from 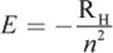 ). Note that unlike other equations, this is initial minus final; the negative sign in the equation accounts for absorption and emission. Thus, a positive E corresponds to emission, and a negative E corresponds to absorption.
). Note that unlike other equations, this is initial minus final; the negative sign in the equation accounts for absorption and emission. Thus, a positive E corresponds to emission, and a negative E corresponds to absorption.
Atomic Absorption Spectra
When an electron is excited to a higher energy level, it must absorb exactly the right amount of energy to make that transition. This means that exciting the electrons of a particular element results in energy absorption at specific wavelengths. Thus, in addition to a unique emission spectrum, every element possesses a characteristic absorption spectrum. Not surprisingly, the wavelengths of absorption correspond exactly to the wavelengths of emission because the difference in energy between levels remains unchanged. Identification of elements in the gas phase requires absorption spectra.
BRIDGE
ΔE is the same for absorption or emission between any two energy levels according to the conservation of energy, as discussed in Chapter 2 of MCAT Physics and Math Review. This is also the same as the energy of the photon of light absorbed or emitted.
Atomic emission and absorption spectra are complex topics, but the takeaway is that each element has a characteristic set of energy levels. For electrons to move from a lower energy level to a higher energy level, they must absorb the right amount of energy to do so. They absorb this energy in the form of light. Similarly, when electrons move from a higher energy level to a lower energy level, they emit the same amount of energy in the form of light.
REAL WORLD
Absorption is the basis for the color of compounds. We see the color of the light that is not absorbed by the compound.
MCAT Concept Check 1.3:
Before you move on, assess your understanding of the material with these questions.
Note: For these questions, try to estimate the calculations without a calculator to mimic Test Day conditions. Double-check your answers with a calculator and refer to the answers for confirmation of your results.
1. The valence electron in a lithium atom jumps from energy level n = 2 to n = 4. What is the energy of this transition in joules? In eV? (Note:
![]()
2. If an electron emits 3 eV of energy, what is the corresponding wavelength of the emitted photon? (Note: 1 eV = 1.60 × 10−19 J, h = 6.626 × 10−34 J · s)
3. Calculate the energy of a photon of wavelength 662 nm. (Note: h = 6.626 × 10−34 J · s)