MCAT General Chemistry Review
Chapter 8: The Gas Phase
8.4 Real Gases
Throughout our discussions of the laws and theory that describe and explain the behaviors of gases, we have stressed that the fundamental assumption is a gas that behaves ideally. However, our world is not one of ideal gases but rather real ones. Real gases have particles that occupy nonnegligible volumes and that interact with each other in measurable ways. In general, the ideal gas law is a good approximation of the behavior of real gases, but all real gases deviate from ideal gas behavior to some extent, particularly when the gas atoms or molecules are forced into close proximity under high pressure (at low volume) and at low temperature. These effects are implied by Figure 8.11, which shows isothermal lines on a pressure–volume graph for a real gas. Compare these lines to the ideal isotherms in Figure 8.2. Under these nonideal conditions, the intermolecular forces and the particles’ volumes become significant.
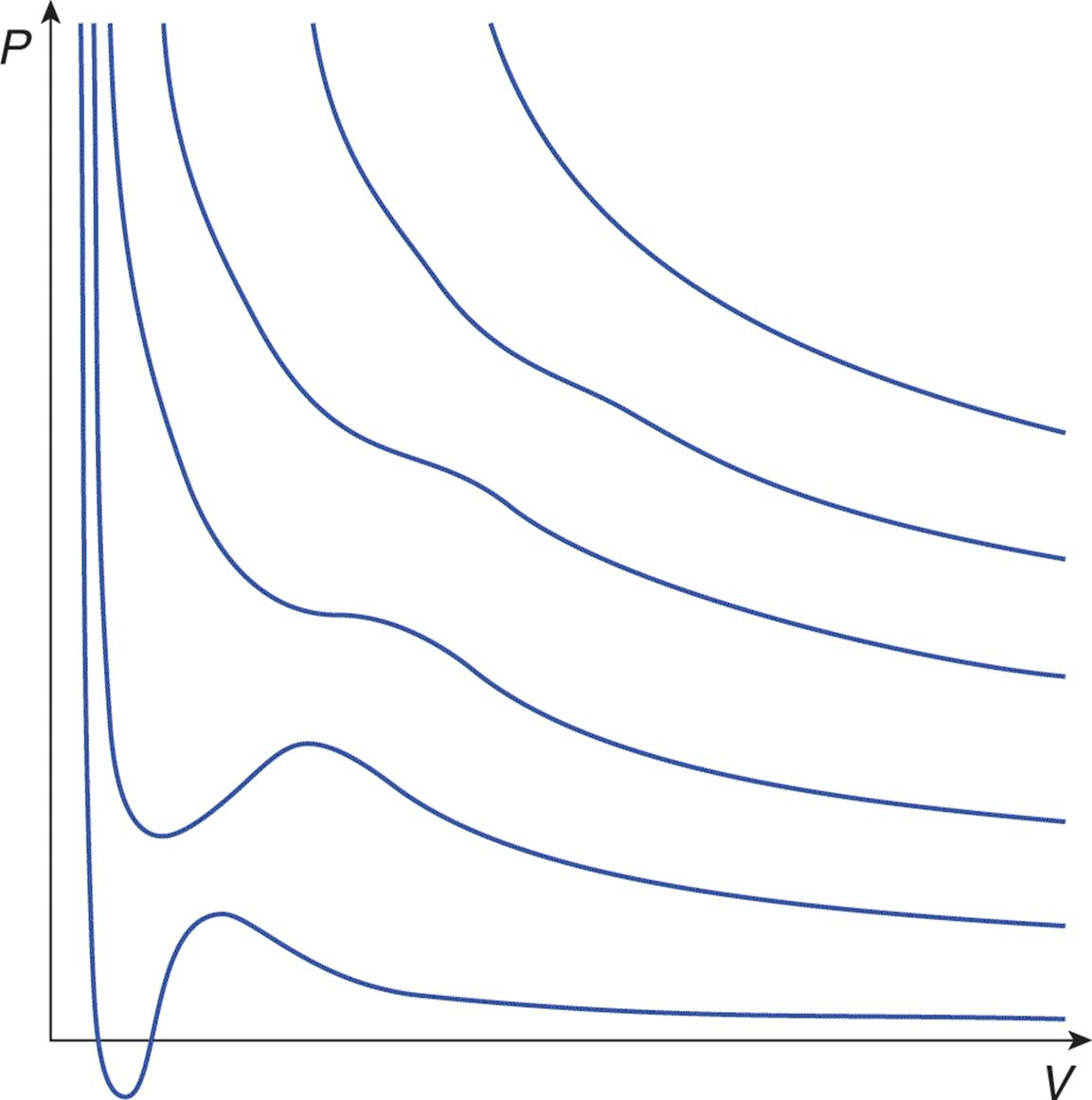 Figure 8.11. Real Gas Isothermal Curves Compare these lines to the ideal gas isotherms in Figure 8.2.
Figure 8.11. Real Gas Isothermal Curves Compare these lines to the ideal gas isotherms in Figure 8.2.
MCAT EXPERTISE
At high temperature and low pressure (high volume), deviations from ideality are usually small; good approximations can still be made from the ideal gas law.
DEVIATIONS DUE TO PRESSURE
As the pressure of a gas increases, the particles are pushed closer and closer together. As the condensation pressure for a given temperature is approached, intermolecular attraction forces become more and more significant, until the gas condenses into a liquid.
MCAT EXPERTISE
On the MCAT, an understanding of nonideal conditions will help with determining how gases’ behaviors may deviate.
At moderately high pressure (a few hundred atmospheres), a gas’s volume is less than would be predicted by the ideal gas law due to intermolecular attraction. At extremely high pressures, however, the size of the particles becomes relatively large compared to the distance between them, and this causes the gas to take up a larger volume than would be predicted by the ideal gas law. That is, while the ideal gas law assumes that a gas can be compressed to take up zero volume, this is not actually physically possible—the gas particles themselves will take up space.
DEVIATIONS DUE TO TEMPERATURE
As the temperature of a gas is decreased, the average speed of the gas molecules decreases and the attractive intermolecular forces become increasingly significant. As the condensation temperature is approached for a given pressure, intermolecular attractions eventually cause the gas to condense to a liquid state.
Like deviations due to pressure, as the temperature of a gas is reduced toward its condensation point (which is the same as its boiling point), intermolecular attraction causes the gas to have a smaller volume than that which would be predicted by the ideal gas law. The closer a gas is to its boiling point, the less ideally it acts. At extremely low temperatures, gases will again occupy more space than predicted by the ideal gas law because the particles cannot be compressed to zero volume.
VAN DER WAALS EQUATION OF STATE
There are several gas equations that attempt to correct for the deviations from ideality that occur when a gas does not closely follow the ideal gas law. The van der Waals equation of state is one such equation:
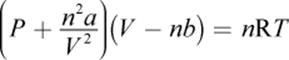
Equation 8.14
where a and b are physical constants experimentally determined for each gas. The a term corrects for the attractive forces between molecules and, as such, will be smaller for gases that are small and less polarizable (such as helium), larger for gases that are larger and more polarizable (such as Xe or N2), and largest for polar molecules such as HCl and NH3. The b term corrects for the volume of the molecules themselves. Larger molecules thus have larger values of b. Numerical values for a are generally much larger than those for b.
KEY CONCEPT
Note that if a and b are both zero, the van der Waals equation of state reduces to the ideal gas law.
MNEMONIC
· a is the van der Waals term for the attractive forces.
· b is the van der Waals term for big particles.
Example:
By what percentage does the real pressure of 1 mole of ammonia in a 1 liter flask at 0°C deviate from its ideal pressure? (Note: ![]() for NH3, a = 4.2, b = 0.037)
for NH3, a = 4.2, b = 0.037)
Solution:
According to the ideal gas law,
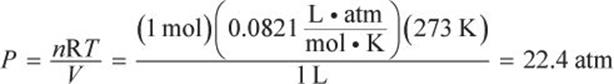
According to the van der Waals equation of state,
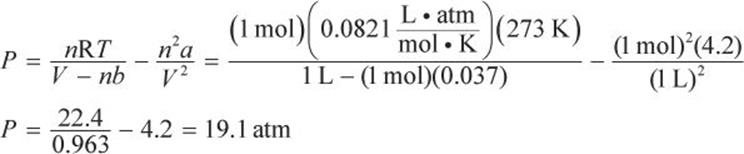
The pressure is thus 3.3 atm less than would be predicted from the ideal gas law, representing an error of
![]()
MCAT EXPERTISE
Be familiar with the concepts embodied by this equation but do not bother memorizing it; if the testmakers want you to apply the equation, it will be provided in a passage or question stem.
MCAT Concept Check 8.4:
Before you move on, assess your understanding of the material with these questions.
1. In what ways do real gases differ from ideal gases?
2. If the attractive forces between gas molecules were to increase while the actual volumes of the molecules remained negligible, what would occur?
3. If the volumes of gas molecules were to increase while the attractive forces between the molecules remained negligible, what would occur?