MCAT General Chemistry Review

Chapter 9: Solutions

9.3 Solution Equilibria

The process of solvation, like other reversible chemical and physical processes, tends toward an equilibrium position, defined as the lowest energy state of a system under a given set of temperature and pressure conditions. Systems move spontaneously toward the equilibrium position, and any movement away from equilibrium is nonspontaneous. In the process of creating a solution, the equilibrium is defined as the saturation point, where the solute concentration is at its maximum value for the given temperature and pressure. Immediately after solute has been introduced into a solvent, most of the change taking place is dissociation because no dissolved solute is initially present. However, once solute is dissolved, the reverse process—precipitation of the solute—will begin to occur.

When the solution is dilute (unsaturated), the thermodynamically favored process is dissolution, and initially, the rate of dissolution will be greater than the rate of precipitation. As the solution becomes more concentrated and approaches saturation, the rate of dissolution lessens, while the rate of precipitation increases. Eventually, the saturation point of the solution is reached, and the solution exists in a state of dynamic equilibrium for which the rates of dissolution and precipitation are equal, and the concentration of dissolved solute reaches a steady-state (constant) value. Neither dissolution nor precipitation is more thermodynamically favored at equilibrium because favoring either would necessarily result in the solution no longer being in a state of equilibrium. At this point, the change in free energy is zero, as is the case for all systems at equilibrium.

An ionic solid introduced into a polar solvent dissociates into its component ions, and the dissociation of such a solute in solution may be represented by

AmBn (s) ⇌ m An⁺ (aq) + n Bm⁻ (aq)

On Test Day, the first step for any solution stoichiometry or solution equilibrium question is to write out the balanced dissociation reaction for the ionic compound in question. This first step is essential for correctly calculating the solubility product constant, ion product, molar solubility, or for determining the outcome of the common ion effect. In other words, it is the essential first step for nearly every solution chemistry problem on the MCAT.

SOLUBILITY PRODUCT CONSTANTS

Most solubility problems on the MCAT deal with solutions of sparingly soluble salts, which are ionic compounds that have very low solubility in aqueous solutions. You may wonder why any ionic compound would not be highly soluble in water. The degree of solubility is determined by the relative changes in enthalpy and entropy associated with the dissolution of the ionic solute at a given temperature and pressure. One common sparingly soluble salt is silver chloride, AgCl, which dissociates in water according to the following equation:

AgCl (s) → Ag⁺ (aq) + Cl⁻ (aq)

The law of mass action can be applied to a solution at equilibrium; that is to say, when the solution is saturated and the solute concentration is at a maximum and is dynamically stable. For a saturated solution of an ionic compound with the formula AmBn, the equilibrium constant for its solubility in aqueous solution, called the solubility product constant (Ksp), can be expressed by

K_sp = [An+]m[Bm–]n

Equation 9.6

where the concentrations of the ionic constituents are equilibrium (saturation) concentrations. For example, we can express the K_sp of silver chloride as:

K_sp = [Ag⁺][Cl⁻]

MCAT EXPERTISE

On the MCAT, if you remember that K_sp is just a specialized form of K_eq, then you can simplify a lot of problems by using the same concepts that you do for all equilibria, including Le Châtelier’s principle.

You’ll notice that, for the law of mass action of solutions, there is no denominator. Remember that pure solids and liquids do not appear in the equilibrium constant. Because the silver chloride solution was formed by adding pure solid silver chloride to pure water, neither the solid silver chloride nor the water is included. Indeed, dissolution reactions—by definition—have a solid salt as a reactant; thus, K_sp expressions should never have denominators.

Solubility product constants, like all other equilibrium constants (K_eq, K_a, K_b, and K_w) are temperature dependent. When the solution consists of a gas dissolved into a liquid, the value of the equilibrium constant, and hence the position of equilibrium (saturation), will also depend on pressure. Generally speaking, the solubility product constant increases with increasing temperature for non-gas solutes and decreases for gas solutes. Higher pressures favor dissolution of gas solutes, and therefore the K_sp will be larger for gases at higher pressures than at lower ones.

REAL WORLD

Because gases become more soluble in solution as pressure increases, a diver who has spent time at significant depths under water will have more nitrogen gas dissolved in his or her blood because nitrogen gas is the main inert gas in the air we breathe. If the diver rises to the surface too quickly, the abrupt decompression will lead to an abrupt decrease in gas solubility in the plasma, resulting in the formation of nitrogen gas bubbles in the bloodstream. The gas bubbles can get lodged in the small vasculature of the peripheral tissue, mostly around the large joints of the body, causing pain and tissue damage (hence the name, the bends). The condition is painful and dangerous and can be fatal if not properly treated.

As solute dissolves into the solvent, the system approaches saturation, at which point no more solute can be dissolved and any excess will precipitate to the bottom of the container. We may not know whether the solution has reached saturation, and so to determine where the system is with respect to the equilibrium position, we can calculate a value called the ion product (IP), which is analogous to the reaction quotient, Q, for other chemical reactions. The ion product equation has the same form as the equation for the solubility product constant:

IP = [An+]m[Bm–]n

Equation 9.7

The difference is that the concentrations used in the ion product equation are the concentrations of the ionic constituents at that given moment in time, which may differ from equilibrium concentrations. As with the reaction quotient Q, the utility of the ion product lies in comparing its value to that attained at equilibrium, K_sp. Each salt has its own distinct K_sp at a given temperature and pressure. If, at a given set of conditions, a salt’s IP is less than the salt’s K_sp, then the solution is not yet at equilibrium and is considered unsaturated. For unsaturated solutions, dissolution is thermodynamically favored over precipitation. If the IP is greater than the K_sp, then the solution is beyond equilibrium, and the solution is considered supersaturated. It is possible to create a supersaturated solution by dissolving solute into a hot solvent and then slowly cooling the solution. A supersaturated solution is thermodynamically unstable, and any disturbance to the solution, such as the addition of more solid solute or other solid particles, or further cooling of the solution, will cause spontaneous precipitation of the excess dissolved solute. If the calculated IP is equal to the known K_sp, then the solution is at equilibrium—the rates of dissolution and precipitation are equal—and the solution is considered saturated. The molarity of a solute in a saturated solution is called the molar solubility of that substance.

KEY CONCEPT

· IP < K_sp: unsaturated, solute will continue to dissolve

· IP = K_sp: saturated, solution is at equilibrium

· IP > K_sp: supersaturated, precipitation will occur

Example:

The molar solubility of Fe(OH)₃ in an aqueous solution was determined to be What is the value of the K_sp for Fe(OH)₃ at the same temperature and pressure?

Solution:

The molar solubility is given as 4 × 10⁻¹⁰ M. The equilibrium concentration of each ion can be determined from the molar solubility and the balanced dissociation reaction of Fe(OH)₃. The dissociation reaction is:

Fe(OH)₃ (s) → Fe³⁺ (aq) + 3 OH⁻ (aq)
K_sp = [Fe³⁺][OH⁻]³

If the molar solubility is 4 × 10⁻¹⁰ M, then 4 × 10⁻¹⁰ M Fe(OH)₃ has dissolved, yielding 4 × 10⁻¹⁰ M Fe³⁺ and 3 × 4 × 10⁻¹⁰ M OH⁻ (because there are three OH⁻ ions given off per Fe(OH)₃ molecule). Thus,

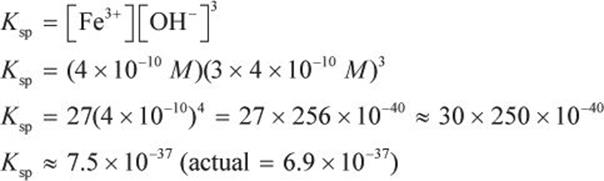
Example:

What are the concentrations of each of the ions in a saturated solution of PbI₂, given that the K_sp of PbI₂ is 8.5 × 10⁻⁹ at standard conditions? If 5 g PbI₂ are dissolved in water to make 1 L of solution at 25°C, would the solution be saturated, unsaturated, or supersaturated?

Solution:

The first step is to write out the dissociation reaction:

PbI₂ (s) → Pb²⁺ (aq) + 2 I⁻ (aq)
K_sp = [Pb²⁺][I⁻]²

Let x equal the concentration of Pb²⁺ at equilibrium. Then, 2x equals the concentration of I⁻ at equilibrium because [I⁻] is two times [Pb²⁺], based on the stoichiometric coefficients.

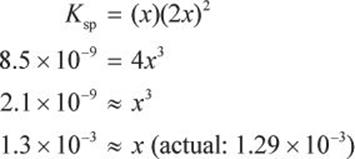
Therefore, [Pb²⁺] is about 1.3 × 10⁻³ M, and [I⁻] is about 2.6 × 10⁻³ M. Note that 1.3 × 10⁻³ M also represents the molar solubility of lead(II) iodide.

Next, we convert 5 g of PbI₂ into moles:

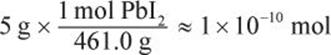
1 × 10⁻² mol PbI₂ in 1 L of solution represents a molarity of 1 × 10⁻² M, which is almost ten times higher than the molar solubility. Therefore, this is a supersaturated solution.

KEY CONCEPT

Every sparingly soluble salt of general formula MX will have K_sp = x², where x is the molar solubility (assuming no common ion effect).

KEY CONCEPT

Every sparingly soluble salt of general formula MX₂ will have K_sp = 4x³, where x is the molar solubility (assuming no common ion effect).

KEY CONCEPT

Every sparingly soluble salt of general formula MX₃ will have K_sp = 27x⁴, where x is the molar solubility (assuming no common ion effect).

Finally, let’s return to our discussion of complex ions and their solubility factors. Much like the examples we have seen previously, the solubility of complex ion solutions is determined by the K_sp. The formation of complex ions increases the solubility of a salt in solution.

For instance, consider free iron(III) (Fe³⁺) in a solution of water. If a cyanide solution were added, an exceptionally stable iron and cyanide metal complex would form as the water molecules solvating the iron are replaced by excess cyanide ions:

Knowing the intricacies of why complexes are more stable in solution than isolated ions is beyond the scope of the MCAT; however, it should make sense that, if a complex ion contains multiple polar bonds between the ligands and the central metal ion, it should be able to engage in a very large amount of dipole–dipole interactions. This stabilizes the dissolution of the complex ion. The end result is that such complexes tend to have very high K_sp values.

When forming a complex ion, one must often use a mixture of solutions. For this reason, a distinction must be made between the K_sp of the solution and that of the complex ion itself. The dissolution of the original solution is termed K_sp, and the subsequent formation of the complex ion in solution is termed Kf (the formation or stability constant of the complex in solution). An example is shown below in which the diamminesilver(I) complex is formed in a silver chloride solution:

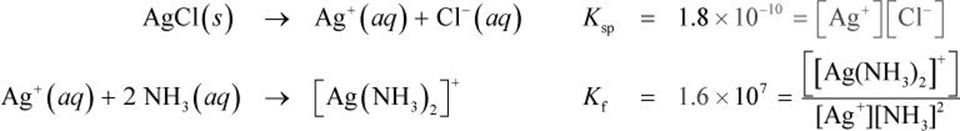
Notice that the formation constant (K_f) of the complex ion is significantly larger than the K_sp of the compound providing the metal ion. This is part of the explanation for why the initial dilution of the metal ion is the rate-limiting step of complex ion formation. However, Le Châtelier’s principle is at play in these reactions as well. Ultimately, complex ions form to become more soluble in solution. And as the amount of silver ion is being used up to form the complex ion itself, the dissociation reaction of AgCl shifts to the right, providing more silver for complex ion formation.

Example:

A 0.1 mol sample of CuS is added to 1.00 L of 1.00 M NH₃. What is the final concentration of the complex ion, tetraamminecopper(II)?

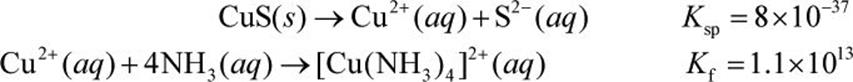
Solution:

First, we must determine the amount of copper ion produced from copper sulfide (CuS) in solution. If the formation of the complex ion occurred simultaneously, we can assume that almost all of the copper ions are liberated from the CuS salt as the dissociation of CuS is driven to completion. Thus,

Using some logic, if x amount of Cu²⁺ is used in complex ion formation, it will require 4x amount of NH₃, forming x amount of the complex ion. Thus, at equilibrium, the concentration of Cu²⁺ is 0.1 M (what was released from CuS) minus x. The concentration of NH₃ will be 1.00M (what was originally present) minus 4x. The concentration of the complex ion will be x.

Now, we can plug into K_f:

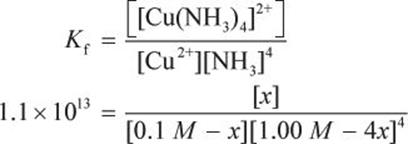
This math is well beyond what the MCAT expects students to be able to do without a calculator, so there must be another way to get to the answer. Consider that the K_f is very large (over 10 trillion!); therefore, the equilibrium is shifted very far to the right. In other words, almost all of the Cu²⁺ ions will be used up to form the complex. Therefore, the concentration of the complex ion is 0.1 M.

COMMON ION EFFECTS

The solubility of a substance varies depending on the temperature of the solution, the solvent, and in the case of a gas-phase solute, the pressure. Solubility is also affected by the addition of other substances to the solution. The effect of a complex ion increasing the solubility of a substance is not typical and is—in fact—opposite to the effect seen in many mixtures of solutions.

One of the more common solution chemistry problems on the MCAT is calculation of the equilibrium concentration of a salt in a solution that already contains one of the ions in that salt. The solubility of a salt is considerably reduced when it is dissolved in a solution that already contains one of its constituent ions as compared to its solubility in a pure solvent. This reduction in molar solubility is called the common ion effect. As described above, the molar solubility of a compound is its concentration (in moles per liter) at equilibrium at a given temperature. If X moles of AmBn (s) can be dissolved in one liter of solution to reach saturation, then the molar solubility of AmBn (s) is X molar.

Pay attention to the effect of the common ion: its presence results in a reduction in the molar solubility of the salt. Note, however, that the presence of the common ion has no effect on the value of the solubility product constant itself. For example, if a salt such as CaF₂ is dissolved into water already containing Ca²⁺ ions (from some other salt, perhaps CaCl₂), the solution will dissolve less CaF₂ than would an equal amount of pure water.

The common ion effect is really Le Châtelier’s principle in action. Because the solution already contains one of the constituent ions from the products side of the dissociation equilibrium, the system will shift toward the left side, reforming the solid salt. As a result, molar solubility for the solid is reduced, and less of the solid dissolves in the solution—although the K_sp remains constant.

Example:

The K_sp of AgI in aqueous solution is 1 × 10⁻¹⁶. If a 1 × 10⁻⁵ M solution of AgNO₃ is saturated with AgI, what will be the final concentration of the iodide ion?

Solution:

The concentration of Ag⁺ in the original AgNO₃ solution will be 1 × 10⁻⁵ M because AgNO₃ will fully dissociate. Some amount of AgI will dissociate into the solution. If this amount is called x, the silver concentration will become 1 × 10⁻⁵ M + x. Because no iodide was present in solution until the AgI began dissociating, the concentration of iodide will be x. Thus, the K_sp expression can be written as:

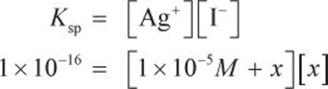
On the MCAT, the value of x is almost always sufficiently small to consider its addition or subtraction from another number negligible. Thus, the math can be simplified to:

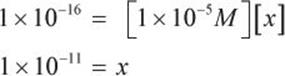
This question asked for the concentration of iodide, which—based on the equilibrium expression—is represented by x. Thus, [I⁻] = 1 × 10⁻¹¹ M.

MCAT Concept Check 9.3:

Before you move on, assess your understanding of the material with these questions.

1. Calculate the K_sp of Ni(OH)₂ in water, given that its molar solubility is 5.2 × 10⁻⁶ M.

2. The K_sp of Ba(OH)₂ is 5.0 × 10⁻³. Assuming that barium hydroxide is the only salt added to form a solution, calculate the ion product of the following solutions based on the concentration of Ba²⁺. Then, predict the behavior of the given solutions (dissolution, equilibrium, or precipitation):

3. What is the solubility of Fe(OH)₂ (K_sp = 1.8 × 10⁻¹⁵) in a 0.1 M solution of NaOH?