MCAT General Chemistry Review
Chapter 11: Oxidation–Reduction Reactions
11.2 Net Ionic Equations
When we discussed reaction types in Chapter 4 of MCAT General Chemistry Review, we left out the rationale for why certain elements come together and others do not. Now that we have discussed oxidation–reduction reactions, it should be clearer that the gain and loss of electrons drives the formation of many compounds, especially ionic ones. Below, we will revisit many important reaction types and understand their basis in oxidation–reduction reactions.
OVERVIEW
In our discussion of acids and bases, we focused only on the presence of protons and hydroxide ions, with little concern for which species actually provided those ions. Similarly, in redox reactions, our focus is on the shifting of electrons more so than the identities of the ions themselves. Consider the following single-displacement reaction:
Zn (s) + CuSO4 (aq) → Cu (s) + ZnSO4 (aq)
If we split the various species into all of the ions present, we get the complete ionic equation:
Zn (s) + Cu2+ (aq) + SO42− (aq) → Cu (s) + Zn2+ (aq) + SO42− (aq)
Note that the sulfate ion is present on both sides of the equation in the same form; this ion is chemically inert during this reaction. In other words, the sulfate is not taking part in the overall reaction but simply remaining in the solution unchanged. We call such species spectator ions. Because the sulfate ion is not involved in the oxidation–reduction reaction, we can simplify the reaction to its net ionic equation, showing only the species that actually participate in the reaction:
Zn (s) + Cu2+ (aq) → Cu (s) + Zn2+ (aq)
When writing net ionic equations, all aqueous compounds should be split into their constituent ions. Solid salts, on the other hand, should be kept together as a single entity. Let’s return to some of the other reactions we have seen previously, including combination, decomposition, combustion, and double-displacement (metathesis) reactions.
MCAT EXPERTISE
Look for compounds such as polyatomic anions that retain their charge before and after reactions; these are usually spectator ions and will not be found in the net ionic equation.
Combination Reactions
In combination reactions, two or more species come together to form a product. For example:
![]()
The relevant half-reactions would be:

The net ionic equation is:
H2 + F2 → 2 H+ + 2 F–
In this reaction, molecular hydrogen acts as a reducing agent as it is oxidized from 0 to +1. Molecular fluorine is the oxidizing agent as it is reduced from 0 to –1. In this reaction, there is no spectator ion.
Decomposition Reactions
In decomposition reactions, one product breaks down into two or more species. For example:
![]()
The relevant half-reactions would be:
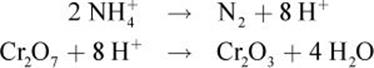
The net ionic equation is:
2 NH4+ + Cr2O72− → N2 + Cr2O3 + 4 H2O
In this reaction, the nitrogen atom in the ammonium cation acts as a reducing agent as it is oxidized from –3 to 0. The chromium in the dichromate anion acts as the oxidizing agent as it is reduced from +6 to +3. In this reaction, there is no spectator ion. Note that the net ionic equation is not significantly different from the original balanced equation
Combustion Reactions
In combustion reactions, a fuel (usually a hydrocarbon) is mixed with an oxidant (usually oxygen), forming carbon dioxide and water. For example:
![]()
The relevant half-reactions would be:

The net ionic equation is identical to the overall balanced equation because there are no spectator ions and no aqueous species:
CH4 + 2 O2 → CO2 + 2 H2O
Combustion reactions can have complex half-reactions, depending on the type of fuel used. In this instance, carbon in methane is the reducing agent as it is oxidized from –4 to +4. Molecular oxygen is the oxidizing agent as it is reduced from 0 to –2.
Double-Displacement (Metathesis) Reactions
Double-displacement or metathesis reactions involve the switching of counterions. Because all ions generally retain their oxidation state, these are not usually oxidation–reduction reactions. For example:
![]()
Because all species retain the same oxidation numbers, this is not considered oxidation–reduction. The net ionic reaction would be:
Ag+ + Cl– → AgCl
The nitrate anion and hydrogen cation both acts as spectator ions in this reaction.
In double-displacement reactions where both reactants and both products are aqueous, there is no net ionic reaction. For example:
![]()
This reaction is not an oxidation–reduction reaction because no species change their oxidation states. Further, because all species are aqueous, the complete ionic reaction is:
Na+ + NO3− + H+ + Cl− → H+ + NO3− + Na+ + Cl−
Because all of the ions appear on both sides of the reaction, there is no net ionic reaction.
DISPROPORTIONATION REACTIONS
Disproportionation (or dismutation) is a specific type of redox reaction in which an element undergoes both oxidation and reduction in producing its products. Many biological enzymes utilize a disproportionation mechanism. An example of such a reaction is the catalysis of peroxides bycatalase, an enzyme found in peroxisomes. Catalase is a critical biological enzyme used to protect cells from excessive oxidation by free radicals or reactive oxygen species. The activity of catalase can be seen when disinfecting a wound with hydrogen peroxide:
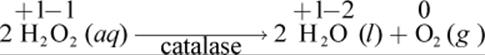
As can be seen from this reaction, oxygen is disproportioned between water and molecular oxygen. In hydrogen peroxide, each oxygen has an oxidation state of –1 (the peroxide ion has a charge of –2 overall). In water, oxygen has an oxidation state of –2, and in molecular oxygen, it has an oxidation state of 0. Therefore, the oxygen is both reduced and oxidized in this reaction.
Another related biological disproportionation mechanism is that of the enzyme superoxide dismutase. As the name implies, a dismutase catalyzes dismutation. This enzyme disproportions oxygen free radicals in the reaction
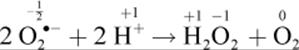
where peroxide and oxygen are the disproportioned products. The oxidation state of oxygen in the free radical is ![]() (a negative charge divided over two oxygen atoms), and it is reduced to –1 in the peroxide and oxidized to 0 in molecular oxygen.
(a negative charge divided over two oxygen atoms), and it is reduced to –1 in the peroxide and oxidized to 0 in molecular oxygen.
Biochemical disproportionation reactions—and oxidation–reduction reactions in biological systems in general—are usually accomplished by enzymes. Structurally, these enzymes often have metals such as Cu and Zn in their active sites that act as reducing agents, as shown in Figure 11.3.
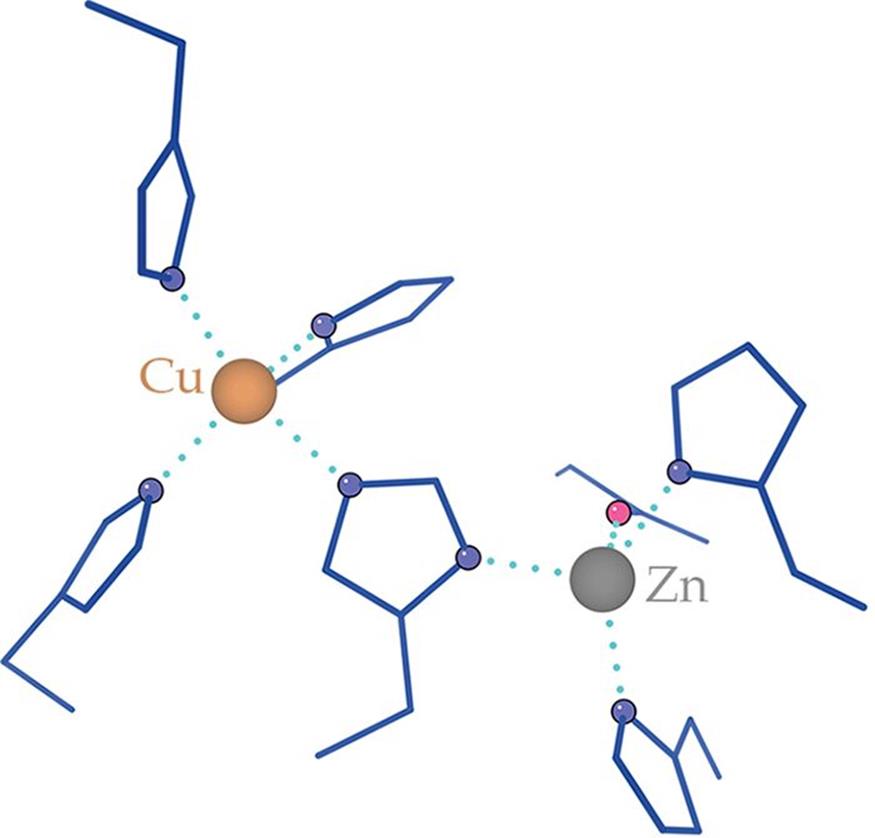 Figure 11.3. Active Site of Superoxide Dismutase Cu and Zn atoms act as reducing agents, losing electrons during catalysis. The atoms are stabilized in position by histidine residues.
Figure 11.3. Active Site of Superoxide Dismutase Cu and Zn atoms act as reducing agents, losing electrons during catalysis. The atoms are stabilized in position by histidine residues.
OXIDATION–REDUCTION TITRATIONS
Oxidation–reduction titrations are similar in setup to acid–base titrations, but the focus is different. Whereas acid–base titrations follow the movement of protons, as discussed in Chapter 10 of MCAT General Chemistry Review, redox titrations follow the transfer of charge (as electrons) to reach the equivalence point. Redox titrations can utilize indicators that change color at a particular voltage (emf) value. Some common indicators are listed in Table 11.2. As for acid–base titrations, it is not necessary to memorize these indicators, but rather to understand their utility.
|
Indicator |
Voltage of Color Change |
Oxidized Form |
Reduced Form |
|
* Safranin is unique in that its color change is not only voltage dependent, but also pH dependent. |
|||
|
Bipyridine metal complexes |
About +1 V |
Colorless (Ru), Cyan (Fe) |
Yellow (Ru), Red (Fe) |
|
Diphenylamine |
+0.76 V |
Violet |
Colorless |
|
Safranin |
+0.24 /–0.29 V* |
Red-Violet |
Colorless |
|
Table 11.2. Common Indicators for Oxidation–Reduction (Redox) Titrations |
|||
One prototypical redox titration involves the use of starch indicators to identify iodine complexes. This specific redox titration is called an iodimetric titration because it relies on the titration of free iodine radicals. The presence of iodine is initially determined by a dark solution in the presence of starch, and at the endpoint of the titration, a colorless solution develops. A common general chemistry laboratory experiment involves the standardization of a thiosulfate solution using iodimetry, as described in the example below.
Example:
A group of students prepares to standardize a Na2S2O3 solution. 32 mL of the Na2S2O3 solution is titrated into 50 mL of a 0.01 M KIO3 solution to reach the equivalence point. They first titrate the KIO3 solution until it loses color, then add a starch indicator until the reaction is complete. The reaction proceeds in these two steps:
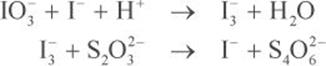
Determine the concentration of the sodium thiosulfate solution at the beginning of the experiment.
Solution:
The titration is performed in two steps. In the first step, the iodate is converted into triiodide anions. The initial titration creates a colorless l3− solution in water, which then requires a starch indicator for the remainder of the titration.
In the second step, the triiodide ions are then reduced in the presence of thiosulfate to determine its concentration. Note that the reactions are unbalanced. It would be tempting to balance the first equation as
IO3− + 2I− + 6H+ → I3− + 3 H2O
However, this reaction has a charge of +3 on the reactants side and –1 on the products side. In oxidation–reduction chemistry, we must balance not only for stoichiometry but also for charge. The correct balanced equations are:
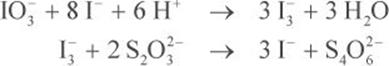
Keeping in mind that each iodate is used to make three triiodide anions, and each triiodide anion interacts with two thiosulfate anions, the mole ratio of thiosulfate to iodate is six to one:
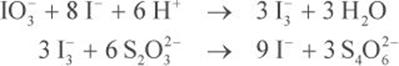
Then, use stoichiometry to determine the molarity of the thiosulfate solution from the 50 mL potassium iodate solution.
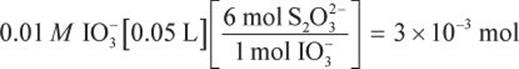
Now, we can use the volume to find the molarity.
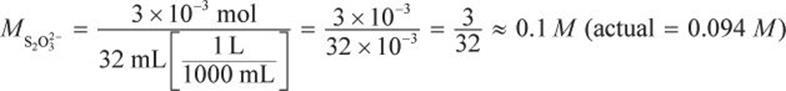
Potentiometric titration is a form of redox titration where no indicator is used. Instead, the electrical potential difference (voltage) is measured using a voltmeter. As a redox titration progresses, its voltage changes; this is analogous to following an acid–base titration with a pH meter instead of a color indicator.
MCAT Concept Check 11.2:
Before you move on, assess your understanding of the material with these questions.
1. Write the net ionic equations for the reactions below:
· CuNO3 (aq) + NaCl (aq) → CuCl (s) + NaNO3(aq)
· Mg (s) + AlCl3 (aq) → Al (s) + MgCl2 (aq)
2. In each of the reactions below, which element undergoes disproportionation? What are that element’s oxidation states in the products?
3 Cl2 (g) + 6 NaOH (aq) → 5 NaCl (aq) + NaClO3 (aq) + 3 H2O (l)
· Element undergoing disproportionation:
· Oxidation states in products:
S2O32− (aq) + 2 H+ (aq) → S (s) + SO2 (g) + H2O (l)
· Element undergoing disproportionation:
· Oxidation states in products:
3. A sample is assayed for lead by a redox titration with I3− (aq). A 10.00 g sample is crushed, dissolved in sulfuric acid, and passed over a reducing agent so that all the lead is in the form Pb2+. The Pb2+ (aq) is completely oxidized to Pb4+ by 32.60 mL of a 0.7 M solution of NaI3. The balanced equation for the reaction is:
I3− + (aq) + Pb2+ (aq) → Pb4+ (aq) + 3I− (aq)
Calculate the mass of lead in the sample.