MCAT General Chemistry Review - Steven A. Leduc 2015

Equilibrium

10.1 EQUILIBRIUM

Many reactions are reversible, and situations can occur in which the forward and reverse reactions come into a balance called equilibrium. How does equilibrium come about? Before any bonds are broken or made, the reaction flask contains only reactants and no products. As the reaction proceeds, products begin to form and eventually build up, and some of them begin to revert to reactants. That is, once products are formed, both the forward and reverse reactions will occur. Ultimately, the reaction will come to equilibrium, a state at which both the forward and reverse reactions occur at the same constant rate. At equilibrium, the overall concentration of reactants and products remains the same, but at the molecular level, they are continually interconverting. Because the forward and reverse processes balance one another perfectly, we don’t observe any net change in concentrations.

When a reaction is at equilibrium (and only at equilibrium), the rate of the forward reaction is equal to the rate of the reverse reaction.

Equilibria occur for closed systems (which means no new reactants, products, or other changes are imposed).

The Equilibrium Constant

Each reaction will tend towards its own equilibrium and, for a given temperature, will have an equilibrium constant, K_eq. For the generic, balanced reaction

a A + b B c C + d D

the equilibrium expression is given by:

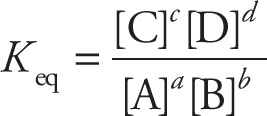
This is known as the mass-action ratio, where the square brackets represent the molar concentrations at equilibrium.

The constant K is often given a subscript to indicate the type of reaction it represents. For example, K_a (for acids), K_b (for bases), and K_sp (for solubility product) are all equilibrium constants. The equilibrium expression is derived from the ratio of the concentration of products to reactants at equilibrium, as follows:

1) Products are in the numerator, and reactants are in the denominator. They are in brackets because the equilibrium expression comes from the concentrations (at equilibrium) of the species in the reaction. For two or more reactants or products, multiply the concentrations of each species together.

2) The coefficient of each species in the reaction becomes an exponent on its concentration in the equilibrium expression.

3) Solids and pure liquids are not included, because their concentrations don’t change. (A substance that’s a solid or pure liquid in the reaction is often indicated by an “(s)” or “(l)” subscript, respectively. We’re also allowed to omit solvents in dilute solutions because the solvents are in vast excess and their concentrations do not change.)

4) Aqueous dissolved particles are included.

5) If the reaction is gaseous, we can use the partial pressure of each gas as its concentration. The value of the equilibrium constant determined with pressures will be different than with concentrations because of their different units. The constant using partial pressures is often termed K_p.

The value of K_eq is constant at a given temperature for a particular reaction, no matter what ratio of reactants and products are given at the beginning of the reaction. That is, any closed system will proceed towards its equilibrium ratio of products and reactants even if you start with all products, or a mixture of some reactants and some products. You can even open the flask and add more of any reactant or product, and the system will change until it has reached the K_eq ratio. We’ll discuss this idea in detail in just a moment, but right now focus on this:

The value of K_eq for a given reaction is a constant at a given temperature.

If the temperature changes, then a reaction’s K_eq value will change.

The value of K_eq tells you the direction the reaction favors:

K_eq < 1 → reaction favors the reactants (i.e., there are more reactants than products at equilibrium)

K_eq = 1 → reaction has roughly equal amounts of reactants and products

K_eq > 1 → reaction favors the products (i.e., there are more products than reactants at equilibrium)

Example 10-1: Which of the following expressions gives the equilibrium constant for this reaction:

2 NO N₂ + O₂?

A) [N₂][O₂]/[2 NO]

B) [N₂][O₂]/[NO]²

C) [NO]/[N₂][O₂]

D) [NO]²/[N₂][O₂]

Solution: The mass-action ratio is products over reactants, so we can immediately eliminate choices C and D. Stoichiometric coefficients become exponents on the concentrations, not coefficients inside the square brackets. Therefore the coefficient of 2 for the reactant NO means the denominator will be [NO]², so the answer is B.

Example 10-2: A certain reversible reaction comes to equilibrium with high concentration of products and low concentration of reactants. Of the following, which is the most likely value of the equilibrium constant for this reaction?

A) K_eq = —1 × 10⁻⁵

B) K_eq = 1 × 10⁻⁵

C) K_eq = 1

D) K_eq = 1 × 10⁵

Solution: First, eliminate choice A since equilibrium constants are never negative. If the concentration of products is high and the concentration of reactants is low at equilibrium, then the ratio “products over reactants” will have a large value certainly greater than 1. Therefore, choice D is the answer.

Example 10-3: When the reaction 2 A + B 2 C reaches equilibrium, [A] = 0.1 M and [C] = 0.2 M. If the value of K_eq for this reaction is 8, what is [B] at equilibrium?

A) 0.1 M

B) 0.2 M

C) 0.4 M

D) 0.5 M

Solution: The expression for K_eq is 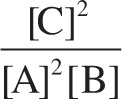. We now solve for [B] and substitute in the given values:

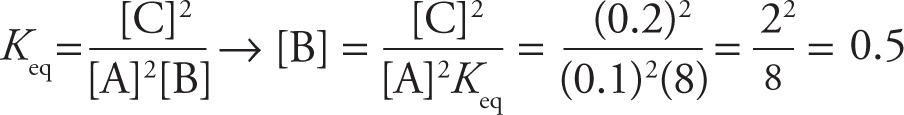
The answer is D.

Example 10-4: Which of the following illustrates a chemical system that is at equilibrium?

I. Bubbles forming in solution

II. A solution saturated with solute

III. The ratio of products to reactants remains constant

A) I only

B) II only

C) I and II only

D) II and III only

Solution: Equilibrium means that the system no longer changes with time. Both II and III illustrate this; therefore, choice D is best.

Example 10-5: The term chemical equilibrium applies to a system:

A) where the forward and reverse reaction have stopped.

B) whose rate law is of zero order.

C) where individual molecules are still reacting, but there is no net change in the system.

D) in which all components are in the same phase.

Solution: A chemical equilibrium is a dynamic equilibrium, which means that molecules are still reacting, but there is no net change in the composition of the system. Choice C is the best choice. Choice A describes a static equilibrium, but all chemical equilibria are dynamic. Choice B refers to rate, but all closed reactions may come to equilibrium, regardless of the order of the reaction. Finally, the term describing choice D is homogeneous, not equilibrium.

10.2 THE REACTION QUOTIENT

The equilibrium constant expression is a ratio: the concentration of the products divided by those of the reactants, each raised to the power equal to its stoichiometric coefficient in the balanced equation. If the reaction is not at equilibrium, the same expression is known simply as the reaction quotient, Q. For the generic, balanced reaction

a A + b B c C + d D

the reaction quotient is given by:

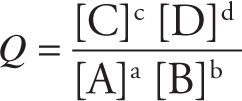
where the square brackets represent the molar concentrations of the species. The point now is that the concentrations in the expression Q do not have to be the concentrations at equilibrium. (If the concentrations are the equilibrium concentrations, the Q will equal K_eq.)

Comparing the value of Q to K_eq tells us in what direction the reaction will proceed. The reaction will strive to reach a state in which Q = K_eq. So, if Q is less than K_eq, then the reaction will proceed in the forward direction (in order to increase the concentration of the products and decrease the concentration of the reactants) to increase Q to the K_eq value. On the other hand, if Q is greater than K_eq, then the reaction will proceed in the reverse direction (in order to increase the concentrations of the reactants and decrease the concentrations of the products) to reduce Q to K_eq.

K_eq is the condition the reaction will try to achieve.

If Q = K_eq, the reaction is at equilibrium.

Example 10-6: The value of the equilibrium constant for the reaction

2 COF₂(g) CO₂(g) + CF₄(g)

is K_eq = 2. If a 1 L reaction container currently holds 1 mole each of CO₂ and CF₄ and 0.5 mole of COF₂, then:

A) the reaction is at equilibrium.

B) the forward reaction will be favored.

C) the reverse reaction will be favored.

D) no prediction can be made without knowing the pressure of the container.

Solution: The expression for Q is 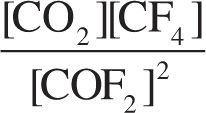. Therefore, the value of Q is:

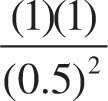= 4

Since Q > K_eq, the reverse reaction will be favored (choice C).

10.3 LE CHÂTELIER’S PRINCIPLE

Le Châtelier’s principle states that a system at equilibrium will try to neutralize any imposed change (or stress) in order to reestablish equilibrium. For example, if you add more reactant to a system that is at equilibrium, the system will react by favoring the forward reaction in order to consume that reactant and reestablish equilibrium.

To illustrate, let’s look at the Haber process for making ammonia:

N₂(g) + 3 H₂(g) 2 NH₃(g) + heat

Let’s assume the reaction is at equilibrium, and see how it reacts to disturbances to the equilibrium by changing the concentration of the species, the pressure, or the temperature.

Adding Ammonia

If we add ammonia, the system is no longer at equilibrium, and there is an excess of product. How can the reaction reestablish equilibrium? By consuming some of the added ammonia, the ratio of products to reactant would decrease towards the equilibrium ratio, so the reverse reaction will be favored (we say the system “shifts to the left”), converting ammonia into nitrogen and hydrogen, until equilibrium is restored.

You can see how this follows from comparing the reaction quotient of the disturbed system to the equilibrium constant. If we add ammonia to the reaction mixture, then [NH₃] increases, and the reaction quotient, Q, becomes greater than K_eq. As a result, the reaction will proceed in the reverse direction in order to reduce Q to K_eq.

Removing Ammonia

If we remove the product, ammonia, then the forward reaction will be favored—the reaction “shifts to the right”—in order to reach equilibrium again. Again, you can see how this follows from comparing the reaction quotient of the disturbed system to the equilibrium constant. If we remove ammonia from the reaction mixture, then [NH₃] decreases, and the reaction quotient, Q, becomes smaller than K_eq. As a result, the reaction will proceed in the forward direction in order to increase Q to K_eq.

Adding Hydrogen

If we add some reactant, say H₂(g), then the forward reaction will be favored—the reaction “shifts to the right”—in order to reach equilibrium again. This follows from comparing the reaction quotient of the disturbed system to the equilibrium constant. If we add hydrogen to the reaction mixture, the [H₂] increases, and the reaction quotient, Q, becomes smaller than K_eq. As a result, the reaction will proceed in the forward direction in order to increase Q to K_eq.

Removing Nitrogen

If we remove some reactant, say N₂(g), then the reverse reaction will be favored—the reaction “shifts to the left”—in order to reach equilibrium again. Again, this follows from comparing the reaction quotient of the disturbed system to the equilibrium constant. If we remove nitrogen from the reaction mixture, then [N₂] decreases, and the reaction quotient, Q, becomes larger than K_eq. As a result, the reaction will proceed in the reverse direction in order to decrease Q to K_eq.

Changing the Volume of the Reaction Container

The Haber process is a gaseous reaction, so a change in volume will cause the partial pressures of the gases to change. Specifically, a decrease in volume of the reaction container will cause the partial pressures of the gases to increase; an increase in volume reduces the partial pressures of the gases in the mixture. If the number of moles of gas on the left side of the reaction does not equal the number of moles of gas on the right, then a change in pressure due to a change in volume will disrupt the equilibrium ratio, and the system will react to reestablish equilibrium.

How does the system react? Let’s first assume the volume is reduced so that the pressure increases. Look back at the equation for the Haber process: There are 4 moles of gas on the reactant side (3 of H₂ plus 1 of N₂) for every 2 moles of NH₃ gas formed. If the reaction shifts to the right, four moles of gas can be condensed into 2 moles, reducing the pressure to reestablish equilibrium. On the other hand, if the volume is increased so that the pressure decreases, the reaction will shift to the left, increasing the pressure to reestablish equilibrium.

To summarize: Consider a gaseous reaction (at equilibrium) with unequal numbers of moles of gas of reactants and products. If the volume is reduced, increasing the pressure, a net reaction occurs favoring the side with the smaller total number of moles of gas. If the volume is expanded, decreasing the pressure, a net reaction occurs favoring the side with the greater total number of moles of gas. (This is only true for reactions involving gases.)

Changing the Temperature of the Reaction Mixture

Heat can be treated as a reactant or a product just like all the chemical reactants and products. Adding or removing heat (by increasing or decreasing the temperature) is like adding or removing any other reagent. Exothermic reactions release heat (which we note on the right side of the equation like a product), and the ∆H will be negative. Endothermic reactions consume heat (which we note on the left side of the equation like a reactant), and the ∆H will be positive.

The Haber process is an exothermic reaction. So, if you increase the temperature at which the reaction takes place once it’s reached equilibrium, the reaction will shift to the left in order to consume the extra heat, thereby producing more reactants. If you decrease the temperature at which the reaction takes place once it’s reached equilibrium, the reaction will shift to the right in order to produce extra heat, thereby producing more product.

Since the reverse of an exothermic reaction is an endothermic one (and vice versa), every equilibrium reaction involves an exothermic reaction and an endothermic reaction. We can then say this: Lowering the temperature favors the exothermic reaction, while raising the temperature favors the endothermic one. Keep in mind that, unlike changes in concentration or pressure, changes in temperature will affect the reaction’s K_eq value, depending on the direction the reaction shifts to reestablish equilibrium.

Note that the above changes are specific to the system once it is at equilibrium. The kinetics of the reaction are a different matter. Remember, all reactions proceed faster when the temperature is increased, and this is true for the Haber process. Indeed, in industry this reaction is typically run at around 500°C, despite the fact that the reaction is exothermic. The reason is that a fast reaction with a 10 percent yield of ammonia may end up being better overall than a painfully slow reaction with a 90 percent yield of ammonia. Heating a reaction gets it to equilibrium faster. Once it’s there, adding or taking away heat will affect the equilibrium as predicted by Le Châtelier’s principle.

Adding an Inert (or Non-Reactive) Gas

What if we injected some helium into a constant volume reaction container? This inert gas doesn’t participate in the reaction (and for the MCAT, inert gases don’t participate in any reaction), so it will change neither the partial pressure nor the concentration of the products or reactants. If neither of these values change, then there is no change in equilibrium.

Adding a Catalyst

Adding a catalyst to a reaction that’s already at equilibrium has no effect. Because it increases the rate of both the forward and reverse reactions equally, the equilibrium amounts of the species are unchanged. So, the introduction of a catalyst would cause no disturbance. Remember that a catalyst increases the reaction rate but does not affect the equilibrium.

Example 10-7: Nitrogen dioxide gas can be formed by the endothermic reaction shown below. Which of the following changes to the equilibrium would not increase the formation of NO₂?

N₂O₄(g) 2 NO₂(g) ∆H = +58 kJ

A) An increase in the temperature

B) A decrease in the volume of the container

C) Adding additional N₂O₄

D) Removing NO₂ as it is formed

Solution: Since ∆H is positive, this reaction is endothermic, and we can think of heat as a reactant. So if we increase the temperature (thereby “adding a reactant,” namely heat), the equilibrium would shift to the right, thus increasing the formation of NO₂. This eliminates choice A. Adding reactant (choice C) or removing product (choice D) would also shift the equilibrium to the right. The answer must be B. A decrease in the volume of the container would increase the pressure of the gases, causing the equilibrium to shift in favor of the side with the fewer number of moles of gases; in this case, that would be to the left.

Example 10-8: If the following endothermic reaction is at equilibrium in a rigid reaction vessel,

CH₄(g) + H₂O(g) CO(g) + 3 H₂(g)

which one of the following changes would cause the equilibrium to shift to the right?

A) Adding Ne(g)

B) Removing some H₂O(g)

C) Increasing the pressure

D) Increasing the temperature

Solution: Choice A would have no effect, since neon is an inert gas and the question states the reaction vessel is rigid, therefore the volume does not change. Removing some reactant (choice B) would shift the equilibrium to the left. An increase in pressure (choice C) would cause the equilibrium to shift in favor of the side with the fewer number of moles of gases; in this case, that would be to the left. The answer must be D. Increasing the temperature of an endothermic reaction will shift the equilibrium toward the products.

Example 10-9: If the reaction

2 NO(g) + O₂(g) 2 NO₂(g) ∆H = —120 kJ

is at equilibrium, which one of the following changes would cause the formation of additional NO₂(g)?

A) Increasing the temperature

B) Adding a catalyst

C) Reducing the volume of the reaction container

D) Removing some NO(g)

Solution: First, eliminate choice B; adding a catalyst to a reaction that’s already at equilibrium has no effect. Now, because ∆H is negative, the reaction is exothermic (that is, we can consider heat to be a product). Increasing the temperature would therefore shift the equilibrium to the left; this eliminates choice A. Also, choice D can be eliminated since removing a reactant shifts the equilibrium to the left. The answer is C: Reducing the volume of the reaction container will increase the pressure, and the equilibrium responds to this stress by favoring the side with the fewer number of moles of gas. In this case, that would mean a shift to the right.

Example 10-10: The Haber process takes place in a container of fixed volume and is at equilibrium:

N₂(g) + 3 H₂(g) 2NH₃(g) + heat

The amounts of the gases present are measured and recorded. Some additional N₂(g) is then injected into the container, and the system is allowed to return to equilibrium. When it does:

A) the amount of H₂ will be smaller than before, and the amounts of N₂ and NH₃ will be greater than before.

B) the amount of N₂ will be smaller than before, and the amounts of H₂ and NH₃ will be greater than before.

C) the amount of NH₃ will be smaller than before, and the amounts of N₂ and H₂ will be greater than before.

D) the amounts of all three gases will be the same as before.

Solution: The system will respond to this change by shifting to the right to reestablish equilibrium. The added N₂ will mean there’s more N₂ in the reaction container, even after equilibrium has been reestablished. Also, the shift toward the product side means there’ll be more NH₃ than before as well. And in the shifting of the equilibrium in an attempt to reestablish equilibrium, some of the H₂ got used. As a result, we’d expect that the amount of H₂ will be smaller than before, while the amounts of N₂ and NH₃ are greater than before the injection of the extra N₂ (choice A).

10.4 SOLUTIONS AND SOLUBILITY

Solutions

A solution forms when one substance dissolves into another, forming a homogeneous mixture. The process of dissolving is known as dissolution. For example, sugar dissolved into iced tea is a solution (though so is unsweetened tea). A substance present in a relatively smaller proportion is called a solute, and a substance present in a relatively greater proportion is called a solvent. The process that occurs when the solvent molecules surround the solute molecules is known as solvation; if the solvent is water, the process is called hydration.

Solutions can involve any of the three phases of matter. For example, you can have a solution of two gases, of a gas in a liquid, of a solid in a liquid, or of a solid in a solid (an alloy). However, most of the solutions with which you’re familiar have a liquid as the solvent. Salt water has solid salt (NaCl) dissolved into water, seltzer water has carbon dioxide gas dissolved in water, and vinegar has liquid acetic acid dissolved in water. In fact, most of the solutions that you commonly see have water as the solvent: lemonade, tea, soda pop, and corn syrup are examples. When a solution has water as the solvent, it is called an aqueous solution.

How do we know which solutes are soluble in which solvents? Well, that’s easy:

Like dissolves like.

Solutes will dissolve best in solvents where the intermolecular forces being broken in the solute are being replaced by equal (or stronger) intermolecular forces between the solvent and the solute.

Electrolytes

When ionic substances dissolve, they dissociate into ions. Free ions in a solution are called electrolytes because the solution can conduct electricity. Some salts dissociate completely into individual ions, while others only partially dissociate (that is, a certain percentage of the ions will remain paired, sticking close to each other rather than being independent and fully surrounded by solvent). Solutes that dissociate completely (like ionic substances) are called strong electrolytes, and those that remain ion-paired to some extent are called weak electrolytes. (Covalent compounds that don’t dissociate into ions are nonelectrolytes.) Solutions of strong electrolytes are better conductors of electricity than those of weak electrolytes.

Different ionic compounds will dissociate into different numbers of particles. Some won’t dissociate at all, and others will break up into several ions. The van’t Hoff (or ionizability) factor (i) tells us how many ions one unit of a substance will produce in a solution. For example,

• C₆H₁₂O₆ is non-ionic, so it does not dissociate. Therefore, i = 1. (Note: The van’t Hoff factor for almost all biomolecules—hormones, proteins, steroids—is 1.)

• NaCl dissociates into Na⁺ and Cl⁻. Therefore, i = 2.

• HNO₃ dissociates into H⁺ and NO₃⁻. Therefore, i = 2.

• CaCl₂ dissociates into Ca²⁺ and 2 Cl⁻. Therefore, i = 3.

Example 10-11: Of the following, which is the weakest electrolyte?

A) NH₄I

B) LiF

C) AgBr

D) H₂O₂

Solution: All ionic compounds, whether soluble or not, are defined as strong electrolytes, so choices A, B, and C are eliminated. Choice D, hydrogen peroxide, is a covalent compound that does not produce an appreciable number of ions upon dissolution and thus is a weak electrolyte. Choice D is the best answer.

The concentration of a solution tells you how much solute is dissolved in the solvent (see Section 3.8). A concentrated solution has a greater amount of solute per unit volume than a solution that is dilute. A saturated solution is one in which no more solute will dissolve. At this point, we have reached the molar solubility of the solute for that particular solvent, and the reverse process of dissolution, called precipitation, occurs at the same rate as dissolving. Both the solid form and the dissolved form of the solute are said to be in dynamic equilibrium.

Example 10-12: A researcher adds 0.4 kg of CaBr₂ (MW = 200 g/mol) to a large flask and adds enough water to make 10 L of solution.

A) What is the molarity of the calcium bromide in the solution?

B) What is the concentration of bromide ion in the solution?

C) How much water would the researcher need to add to the solution in order to decrease the concentration by a factor of 4?

Solution:

A) Since the molecular weight of CaBr₂ is 0.2 kg/mol, a 0.4 kg sample represents 2 moles. Then by definition we have

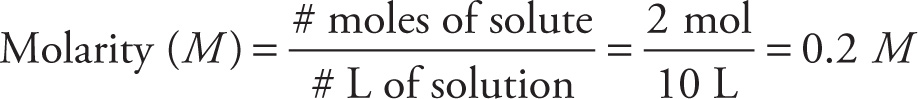
B) Since CaBr₂ dissociates into one Ca²⁺ ion and 2 Br⁻ ions, the concentration of bromide ion in the solution is 2(0.2 M) = 0.4 M.

C) Let x be the number of liters of additional water added to the solution. If the concentration is to be decreased by a factor of 4 (that is, to 0.05 M), then

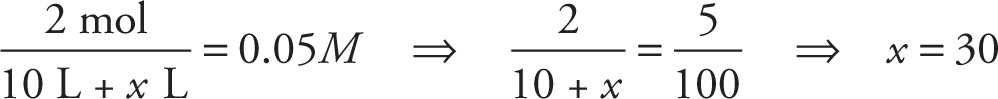
Solubility

Solubility refers to the amount of solute that will saturate a particular solvent. Solubility is specific for the type of solute and solvent. For example, 100 mL of water at 25°C becomes saturated with 40 g of dissolved NaCl, but it would take 150 g of KI to saturate the same volume of water at this temperature. And both of these salts behave differently in methanol than in water. Solubility also varies with temperature, increasing or decreasing with temperature depending upon the solute and solvent as outlined in the first set of solubility rules below.

There are two sets of solubility rules that show up time and time again on the MCAT. The first set governs the general solubility of solids and gases in liquids, as a function of the temperature and pressure. These rules below should be taken as just rules of thumb because they are only 95 percent reliable (still not bad). Memorize the following:

Phase Solubility Rules

1. The solubility of solids in liquids tends to increase with increasing temperature.

2. The solubility of gases in liquids tends to decrease with increasing temperature.

3. The solubility of gases in liquids tends to increase with increasing pressure.

Keep in mind, the solubility of a gas in a liquid is also a function of the partial pressure of that gas above the liquid and the Henry’s law constant (Solubility = kP). As partial pressure increases, the quantity of dissolved gas necessarily increases as the equilibrium constant remains unchanged.

The second set governs the solubility of salts in water. Memorize the following too:

Salt Solubility Rules

1. All Group I (Li⁺, Na⁺, K⁺, Rb⁺, Cs⁺) and ammonium (NH₄⁺) salts are soluble.

2. All nitrate (NO₃⁻), perchlorate (ClO₄⁻), and acetate (C₂H₃O₂⁻) salts are soluble.

3. All silver (Ag⁺), lead (Pb²⁺/ Pb⁴⁺), and mercury (Hg₂²⁺/ Hg²⁺) salts are insoluble, except for their nitrates, perchlorates, and acetates.

Example 10-13: Which of the following salts is expected to be insoluble in water?

A) CsOH

B) NH₄NO₃

C) CaCO₃

D) AgClO₄

Solution: According to the solubility rules for salts in water, choices A, B, and D are expected to be soluble. Choice C is therefore the best answer.

Example 10-14: Which of the following acids could be added to an unknown salt solution and NOT cause precipitation?

A) HCl

B) HI

C) H₂SO₄

D) HNO₃

Solution: According to the solubility rules for salts, all nitrate (NO₃⁻) salts are soluble. Therefore, only the addition of nitric acid guarantees that any new ion combination would be soluble. Choice D is the correct answer.

Example 10-15: Which one of the following observations is inconsistent with the solubility rules given above?

A) More sugar dissolves in a pot of hot water than in a pot of cold water.

B) Boiler scales are caused by the precipitation of CaCO₃ inside plumbing when hot water heaters heat up cold well water.

C) After breathing compressed air at depth, scuba divers that ascend to the surface too quickly risk having air bubbles in their body.

D) Boiling the water before making ice cubes out of it results in clear ice cubes that have no trapped air bubbles.

Solution: Choice A is consistent with phase solubility rule 1, so it is eliminated. Choice C is consistent with phase solubility rule 3, so it is eliminated as well. And finally, choice D is consistent with the second solubility rule 2, so it is also eliminated. Although choice B is a true statement, it is one of those few examples that runs counter to our phase solubility rule 1. Choice B is the correct answer.

Solubility Product Constant

All salts have characteristic solubilities in water. Some, like NaCl, are very soluble, while others, like AgCl, barely dissolve at all. The extent to which a salt will dissolve in water can be determined from its solubility product constant, K_sp. The solubility product is simply another equilibrium constant, one in which the reactants and products are just the undissolved and dissolved salts.

For example, let’s look at the dissolution of magnesium hydroxide in water:

Mg(OH)₂(s) Mg²⁺(aq) + 2 OH⁻(aq)

At equilibrium, the solution is saturated; the rate at which ions go into solution is equal to the rate at which they precipitate out. The equilibrium expression is

K_sp = [Mg²⁺][OH⁻]²

Notice that we leave the Mg(OH)₂ out of the equilibrium expression because it’s a pure solid. (The “concentration of a solid” is meaningless when discussing the equilibrium between a solid and its ions in a saturated aqueous solution.)

Solubility Computations

Let’s say you know the K_sp for a solid, and you’re asked to find out just how much of it can dissolve into water; that is, you’re asked to determine the salt’s molar solubility, the number of moles of that salt that will saturate a liter of water.

To find the solubility of Mg(OH)₂, we begin by figuring out how much of each type of ion we’ll have once we have x moles of the salt. Since each molecule dissociates into one magnesium ion and two hydroxide ions, if x moles of this salt have dissolved, the solution contains x moles of Mg²⁺ ions and 2x moles of OH⁻ ions:

Mg(OH)₂(s) Mg²⁺(aq) + 2OH⁻(aq)

x x + 2x

So, if x stands for the number of moles of Mg(OH)₂ that have dissolved per liter of saturated solution (which is what we’re trying to find), then [Mg²⁺] = x and [OH⁻] = 2x. Substituting these into the solubility product expression gives us

K_sp = [Mg²⁺][OH⁻]²

= x (2x)² = x (4x²) = 4x³

It is known that K_sp for Mg(OH)₂ at 25°C is about 1.6 × 10⁻¹¹. So, if we set this equal to 4x³, we can solve for x. We get x ≈ 1.6 × 10⁻⁴. This means that a solution of Mg(OH)₂ at 25°C will be saturated at a Mg(OH)₂ concentration of 1.6 × 10⁻⁴ M.

Example 10-16: The value of the solubility product for copper(I) chloride is K_sp = 1.2 × 10⁻⁶. Under normal conditions, the maximum concentration of an aqueous CuCl solution will be:

A) less than 10⁻⁶ M.

B) greater than 10⁻⁶ M and less than 10⁻⁴ M.

C) greater than 10⁻⁴ M and less than 10² M.

D) greater than 10⁻² M and less than 10⁻¹ M.

Solution: The equilibrium is CuCl(s) Cu⁺(aq) + Cl⁻(aq). If we let x denote [Cu⁺], then we also have x = [Cl⁻]. Therefore, K_sp = x × x = x²; setting this equal to 1.2 × 10⁻⁶, we find that x is 1.1 × 10⁻³ M. Therefore, the answer is C.

Example 10-17: The solubility product for lithium phosphate, Li₃PO₄, is K_sp = 2.7 × 10⁻⁹. How many moles of this salt would be required to form a saturated, 1 L aqueous solution?

Solution: The equilibrium is Li₃PO₄(s) 3Li⁺(aq) + PO₄^3—(aq). If we let x denote [PO₄^3—], then we have [Li⁺] = 3x. Therefore, K_sp = (3x)³ × x = 27x⁴; setting this equal to 2.7 × 10⁻⁹ = 27 × 10⁻¹⁰ we find that

27x⁴ = 27 × 10⁻¹⁰ → x = (10⁻¹⁰)^1/4 = 10^−2.5 = 10^0.5 × 10⁻³ ≈ 3.2 × 10⁻³

Therefore, 3.2 × 10⁻³ mol will be required.

10.5 ION PRODUCT

The ion product is the reaction quotient for a solubility reaction. That is, while K_sp is equal to the product of the concentrations of the ions in solution when the solution is saturated (that is, at equilibrium), the ion product—which we’ll denote by Q_sp—has exactly the same form as the K_sp expression, but the concentrations don’t have to be those at equilibrium. The reaction quotient allows us to make predictions about what the reaction will do:

Q_sp < K_sp → more salt can be dissolved

Q_sp = K_sp → solution is saturated

Q_sp > K_sp → excess salt will precipitate

For example, let’s say we had a liter of solution containing 10⁻⁴ mol of barium chloride and 10⁻³ mol of sodium sulfate, both of which are soluble salts:

BaCl₂(s) → Ba²⁺(aq) + 2Cl⁻(aq)

Na₂SO₄(s) → 2Na⁺(aq) + SO₄^2—(aq)

When you mix two salts in solution, ions can recombine to form new salts, and you have to consider the new salt’s K_sp. Barium sulfate, BaSO₄, is a slightly soluble salt, and at 25°C, its K_sp is 1.1 × 10⁻¹⁰. Its dissolution equilibrium is

BaSO₄(s) Ba²⁺(aq) + SO₄^2—(aq)

Its ion product is Q _sp = [Ba²⁺][SO₄^2—], so in this solution, we have Q_sp = (10⁻⁴)(10⁻³) = 10⁻⁷, which is much greater than its K_sp. Since Q_sp > K_sp, the reverse reaction would be favored, and BaSO₄ would precipitate out of solution.

10.6 THE COMMON-ION EFFECT

Let’s consider again a saturated solution of magnesium hydroxide:

Mg(OH)₂(s) Mg²⁺(aq) + 2OH⁻(aq)

What would happen if we now added some sodium hydroxide, NaOH, to this solution? Since NaOH is very soluble in water, it will dissociate completely:

NaOH(s) → Na⁺(aq) + OH⁻(aq)

The addition of NaOH has caused the amount of hydroxide ion—the common ion—in the solution to increase. This disturbs the equilibrium of magnesium hydroxide; since the concentration of a product of that equilibrium is increased, Le Châtelier’s principle tells us that the system will react by favoring the reverse reaction, producing solid Mg(OH)₂, which will precipitate. Therefore, the molar solubility of the slightly soluble salt [in this case, Mg(OH)₂] is decreased by the presence of another solute (in this case, NaOH) that supplies a common ion. This is the common-ion effect.

Example 10-18: Barium chromate solid (K_sp = 1.2 × 10⁻¹⁰) is at equilibrium with its dissociated ions in an aqueous solution. If calcium chromate (K_sp = 7.1 × 10⁻⁴) is introduced into the solution, it will cause the molar quantity of:

A) solid barium chromate to increase and barium ion to decrease.

B) solid barium chromate to increase and barium ion to increase.

C) solid barium chromate to decrease and barium ion to decrease.

D) solid barium chromate to decrease and barium ion to increase.

Solution: The answer is A. The introduction of additional chromate ion (CrO₄^2—)—the common ion—will cause the amount of barium ion in solution to decrease (since the solubility equilibrium of BaCrO₄ will be shifted to the left, consuming Ba²⁺). And, as a result, the amount of solid barium chromate will increase, because some will precipitate.

Example 10-19: A researcher wishes to prepare a saturated solution of a lead compound that contains the greatest concentration of lead(II) ions. Of the following, which should she use?

A) Pb(OH)₂ (K_sp = 2.8 × 10⁻¹⁶)

B) PbCl₂ (K_sp = 1.7 × 10⁻⁵)

C) PbI₂ (K_sp = 8.7 × 10⁻⁹)

D) PbBr₂ (K_sp = 6.3 × 10⁻⁶)

Solution: Since the equilibrium had the form PbX₂(s) Pb²⁺(aq) + 2 X⁻(aq), we have K_sp = [Pb²⁺][X⁻]². Therefore, to maximize [Pb²⁺], the researcher would want to maximize K_sp. Of the choices given, PbCl₂ (choice B) has the largest K_sp value.

10.7 COMPLEX ION FORMATION AND SOLUBILITY

Complex ions consist of metallic ions surrounded by generally two, four, or six ligands, also known as Lewis bases. Complexed metal ions may have extremely different solubility properties than the “naked,” hydrated metal ions. Therefore, the addition of ligands may substantially alter the solubility of simple metal salts. For example, as described by the solubility rules in Section 10.4 above, silver chloride (AgCl) is largely insoluble in water as is evident by its extremely low K_sp (1.7 × 10⁻¹⁰). However, addition of AgCl to an aqueous solution containing ammonia (NH₃) results in greater solubility, owing to the formation of the complex ion [Ag(NH₃)₂]⁺. The overall effect is described by the equations below:

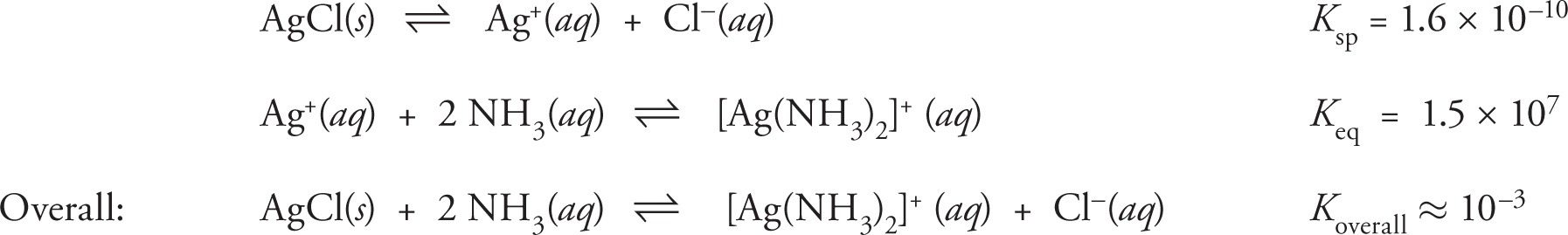
The inclusion of ammonia in the system greatly increases the propensity of the AgCl(s) to exist as ions in solution. While the final value of K (10⁻³) is still less than 1, it is several orders of magnitude greater than the initial K_sp of AgCl. The dissolution of the initial silver salt can be favored even more by taking advantage of Le Châtelier’s Principle through the simple addition of excess ammonia.

One biological application of complex ion formation is metal-chelation therapy; one of the most commonly used metal chelation agents, ethylenediaminetetraacetic acid (EDTA) is approved by the FDA for the treatment of acute lead poisoning. After the administration of EDTA (generally as a mixed calcium/sodium salt), an equilibrium is established, sequestering the toxic Pb²⁺ ions in the patient’s system in a very stable EDTA complex. The following reaction demonstrates the association of fully deprotonated EDTA and Pb²⁺ to form the complex ion:

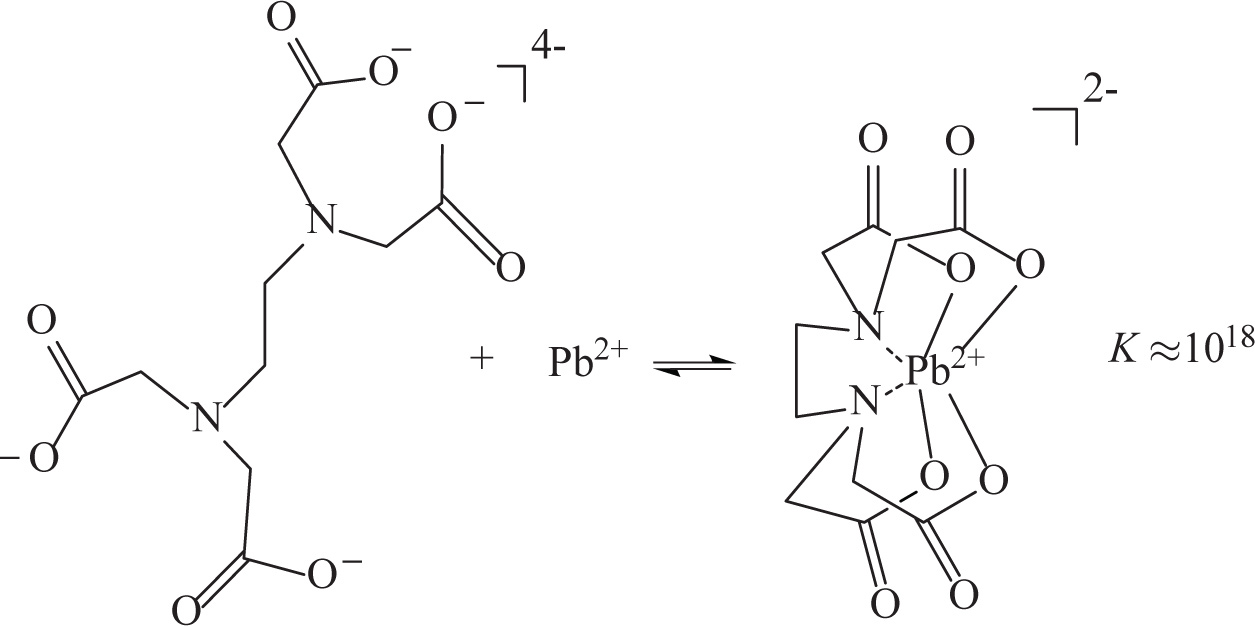
The extremely high equilibrium constant for the formation of the complexed Pb²⁺ ensures that it is prevented from further deleterious interactions with other biological functionalities, and allows its speedy excretion from the body.

10.8 THERMODYNAMICS AND EQUILIBRIUM

In Section 6.5 on Gibbs Free Energy, we saw that if ∆G was negative we could expect a reaction to proceed spontaneously in the forward direction, with the opposite being true for the case in which ∆G is positive. When a system proceeds in one direction or another there is necessarily a change in the relative values of products and reactants that redefine ∆G, and the reaction proceeds until ∆G is equal to 0 and equilibrium is achieved. Therefore, there must be a relationship between ∆G and the reaction quotient Q, as well as the equilibrium constant K_eq. This relationship is given in the following equation.

∆G = ∆G° + RT lnQ

As the superscript denotes, ∆G° is the Gibbs free energy for a reaction under standard conditions. You may recall from Section 10.2 that when Q = K the reaction is at equilibrium. Since ∆G is always equal to zero at equilibrium we can change the equation to

0 = ∆G° + RT lnK_eq

or

∆G° = —RT lnK_eq

It is important to draw the distinction between ∆G and ∆G°. Whereas ∆G is a statement of spontaneity of a reaction in one direction or another, ∆G° is, as seen in its relation to K_eq, a statement of the relative proportions of products and reactants present at equilibrium. The standard state ∆G° for a reaction only describes a reaction at one specific temperature, pressure, and set of concentrations, whereas ∆G changes with changing reaction composition until it reaches zero. From the above relationship, we can surmise the following:

∆G° < 0 ; K_eq > 1, products are favored at equilibrium

∆G° = 0 ; K_eq = 1, products and reactants are present in roughly equal amounts at equilibrium

∆G° > 0 ; K_eq < 1, reactants are favored at equilibrium

The difference between the heights of the reactants and products on any reaction coordinate diagram is ∆G°. As we know from analyzing these plots if the reactants are higher than the products, we expect the products to be favored. This would give us the expected negative value of ∆G°, and likewise a value of K_eq greater than 1.

Chapter 10 Summary

• The equilibrium constant dictates the relative ratios of products to reactant when a system is at equilibrium.

• For aA + bB → cC + dD: K_eq = ([C]^c[D]^d)/([A]^a[B]^b)

• Pure solids and liquids are not included in the equilbrium expression.

• If K > 1, products are favored. If K < 1 reactants are favored.

• The reaction quotient, Q, is a ratio of products and reactants with the same form as K, but can be used when the reaction isn’t at equilibrium. If Q < K, the reaction will proceed in the forward reaction; if Q > K, the reaction will proceed in the reverse direction until equilibrium is achieved.

• The only factor that changes the equilibrium constant is temperature.

• Changing the concentrations of the products or reactants of a reaction at equilibrium will force the system to shift according to Le Châtelier’s principle.

• Increasing the temperature of a system at equilibrium favors the products in an endothermic reaction and the reactants in an exothermic reaction. Decreasing the temperature will have the opposite effect on both types of reactions.

• In a gaseous reaction, increasing the pressure by decreasing the volume favors the side of the reaction with fewer moles of gas. Decreasing the pressure has the opposite effect.

• An electrolyte is a solute that produces free ions in solution. Strong electrolytes produce more ions in solution than weak electrolytes.

• The van’t Hoff (or ionizability) factor, i, tells us how many ions one unit of a substance will produce in solution.

• All Group I, ammonium, nitrate, perchlorate, and acetate salts are completely soluble. All silver, lead, and mercury salts are insoluble, except when they are paired with nitrate, perchlorate, or acetate.

• The solubility of solids in liquids increases with increasing temperature.

• The solubility of gases in liquids decreases with increasing temperature and increases with increasing pressure.

• The amount of a salt that can be dissolved in a solute is given by its solubility product constant (K_sp).

• For a reaction at equilibrium under standard conditions, ∆G° = −RTlnK_eq.

• For a reaction under non-standard conditions, ∆G can be calculated using ∆G = ∆G° + RTlnQ.

CHAPTER 10 FREESTANDING PRACTICE QUESTIONS

1. Which of the following manipulations is capable of changing the K_eq of the reaction shown below?

N₂ (g) + H₂(g) 2 NH₃(g)

A) Doubling the concentrations of N₂ (g), H₂(g), and NH₃(g)

B) Tripling the volume of the reaction container

C) Increasing the pressure from 1 to 2 atm

D) Decreasing the temperature to from 298 K to 273 K

2. A group of scientists is studying the dynamics of the acetic acid dissociation below and bring the process to equilibrium under standard conditions. If the scientists then add 35 g of sodium acetate to the reaction container, which of the following will be true?

CH₃COOH(aq) CH₃COO⁻(aq) + H⁺ (aq)

A) Q > K_eq and the reaction will move in reverse.

B) Q < K_eq and the reaction will move forward.

C) Q > K_eq and the reaction will move forward.

D) Q < K_eq and the reaction will move in reverse.

3. Given the following equilibrium:

N₂(g) + 3 H₂(g) 2 NH₃(g) ∆H = −91.8kJ

How would an increase in temperature affect the concentration of N₂ at equilibrium?

A) The concentration of N₂ will increase because of an increase in K_eq.

B) The concentration of N₂ will decrease because of an increase in K_eq.

C) The concentration of N₂ will increase because of a decrease in K_eq.

D) The concentration of N₂ will remain unchanged.

4. Na₂SO₄ is soluble in water. If NaCl(s) is added to a solution of Na₂SO₄(aq) so that the concentration of Na⁺ doubles, then the:

A) solubility constant of Na₂SO₄ increases while that of NaCl decreases.

B) solubility constants of Na₂SO₄ and NaCl both decrease.

C) solubility of Na₂SO₄ and NaCl both decrease.

D) solubility of Na₂SO₄ decreases while that of NaCl increases.

5. The equilibrium expression below corresponds to which of the following reactions?

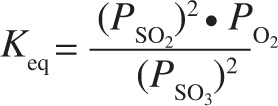
A) 2 SO₂(aq) + O₂(g) 2 SO₃(aq)

B) 2 SO₃(aq) 2 SO₂(aq) + O₂(g)

C) 2 SO₂(g) + O₂(g) 2 SO₃(g)

D) 2 SO₃(g) 2 SO₂(g) + O₂(g)

6. Which of the following salts is least soluble in water?

A) PbI₂ (K_sp = 7.9 × 10⁻⁹)

B) Mg(OH)₂ (K_sp = 6.3 × 10⁻¹⁰)

C) Zn(IO₃)₂ (K_sp = 3.9 × 10⁻⁶)

D) SrF₂ (K_sp = 2.6 × 10⁻⁹)

7. The water solubility of MgSO₄ is approximately 25 g/100 mL at 20°C. Compared to a 0.25 g/mL solution of MgSO₄ prepared at 20°C, a 0.25 g/mL solution prepared at 37°C will:

A) dissolve faster and have the same concentration of ions in solution.

B) dissolve faster and have a higher concentration of ions in solution.

C) dissolve slower and have a lower concentration of ions in solution.

D) dissolve slower and have the same concentration of ions in solution.

8. If the K_sp of KI is 1.45 × 10⁻⁶ in propanol at 25°C, what would the K_sp of KI be in propane at the same temperature?

A) 1.84

B) 2.90 × 10⁻³

C) 1.81 × 10⁻⁶

D) 7.56 × 10⁻²³

9. The K_sp of NaCl in water is 35.9 at 25°C. If 500 mL of 12 M NaOH(aq) and 500 mL of 12 M HCl(aq) solution both at 25°C are combined, what would best describe the resulting solution?

A) A small amount of NaCl(s) would precipitate.

B) There will be a 6 M aqueous solution of NaCl.

C) Enthalpy and entropy would increase.

D) The resulting solution would be slightly basic.

CHAPTER 10 PRACTICE PASSAGE

Many caves trace their roots back to chemical principles. Some caves, called solutional caves, are formed as a result of acidic water flowing through rock such as limestone (CaCO₃, K_sp = 3.4 × 10⁻⁹ at 25°C). In this process limestone is dissolved, resulting in cave formation.

Solutional caves often contain spectacular rock formations. They are the products of equilibria involving water, carbon dioxide and limestone. The process begins when surface water flowing into the caves encounters soil with a higher PCO₂ than found in the atmosphere. This high CO₂ content is a result of CO₂ release from the earth’s mantle, in a process called outgassing. Equation 1 describes the dissolution of CO₂ in water:

CO₂(g) + H₂O(l) CO₂(aq) + H₂O(l)

Equation 1

Once solubilized, CO₂(aq) causes the acidification of water via Equation 2:

CO₂(aq) + H₂O(l) H₂CO₃(aq) H₃O⁺(aq) + HCO₃⁻(aq)

Equation 2

The acidic water causes dissolution of limestone according to the following equilibrium:

Equation 3

When acidic solution finally flows through the roof and into the cave, it encounters ambient air with a lower PCO₂ than that in the soil. As such, dissolved CO₂(aq) is released as a gas, eventually causing the precipitation of CaCO₃(s). This precipitate forms stalagmites, an upward spike formed from water striking the ground in the cave, and stalactites, which are downward spikes created from water flowing down from the roofs toward the ground. Eventually, in a process that can take thousands of years, the two can meet to form a column in the cave.

1. A local factory accidentally pollutes groundwater supplies near a cave with (NH₄₎₂CO₃. How would the cave most likely be affected?

A) Stalagmite and stalactite formation would likely not be affected.

B) Increased groundwater acidity would increase stalagmite and stalactite formation.

C) Increased groundwater acidity would decrease stalagmite and stalactite formation.

D) Cannot be determined from the information given.

2. As the ground temperature surrounding a cave increases, stalactite and stalagmite growth is found to decrease. What is the best explanation for this?

A) Increased heat causes CaCO₃ to melt.

B) Formation of stalactites and stalagmites is endothermic.

C) Increasing temperature decreases the aqueous solubility of CaCO₃.

D) The concentration of CO₂(g) in water increases as temperature increases.

3. What is the approximate concentration of CO₃⁻² when enough CaCO₃(s) is dissolved in water to form a saturated solution?

A) 2.5 × 10⁻⁹ M

B) 5.0 × 10⁻⁹ M

C) 6.0 × 10⁻⁵ M

D) 1.0 × 10⁻⁴ M

4. Which of the following will form a buffer when combined with CaCO₃(aq)?

A) C₂H₄O₂

B) K₂CO₃

C) NaHCO₃

D) CO₂

5. The shape of the carbonate ion is:

A) trigonal planar and the carbon atom is sp³ hybridized.

B) trigonal planar and the carbon atom is sp² hybridized.

C) tetrahedral and the carbon atom is sp² hybridized.

D) tetrahedral and the carbon atom is sp³ hybridized.

6. A stalagmite in a cave suffers damage and researchers want it repaired naturally as quickly as possible. Which of the following will help this process?

A) Adding CaCl₂ to groundwater.

B) Adding chemical compounds in the cave that absorb CO₂ from the air.

C) Increasing the pH of the groundwater supply.

D) Spraying the stalagmite with compressed CO₂.

SOLUTIONS TO CHAPTER 10 FREESTANDING PRACTICE QUESTIONS

1. D Equilibrium constants are specific to a single temperature and standard state free energy change according to: ∆G° = −RTlnK. Altering temperature is the only answer choice that can change the reaction’s K_eq.

2. A K_eq = [products]/[reactants] when both reactant and product concentrations are those at equilibrium. Q = [products]/[reactants] regardless of whether reactant and product concentrations are those at equilibrium. The addition of sodium acetate essentially translates into the addition of acetate ion, a product in this equilibrium. As a result of such an addition, Q > K_eq and products are present in excess of equilibrium values. Le Châtelier’s principle states that net reverse movement is created when the concentration of products is increased in an equilibrium system.

3. C Since the reaction is exothermic, an increase in temperature will shift the equilibrium to the left, and the concentration of N₂ will increase, eliminating choices B and D. For exothermic reactions, an increase in temperature will decrease the K_eq, eliminating choice A and making choice C the correct answer.

4. C Solubility constants, like all equilibrium constants, are functions of temperature only. This eliminates choices A and B. Given the equilibria:

Na₂SO₄(s) 2 Na⁺ (aq) + SO²⁻₄(aq)

NaCl(s) Na⁺ (aq) + Cl⁻ (aq)

Na⁺ is a common ion to both systems. Increasing Na⁺ concentration will decrease the solubility of both salts, eliminating choice D and making choice C the best answer.

5. D The expression is in terms of partial pressure, so all components must be gaseous, eliminating choices A and B. An equilibrium expression has products in the numerator and reactants in the denominator, eliminating choice C. The exponents correspond to the stoichiometric coefficients of the balanced equation, so choice D is correct.

6. B All of the compounds are composed of one cation and two anions, so comparing K_sp values will give relative solubility. Since the question asks for an extreme, the middle values of the variable cannot be correct, eliminating choices A and D. The compound with the lowest K_sp value will have the lowest solubility because for all the compounds, K_sp = [cation][anion]². Therefore, choice B is correct.

7. A This is a two-by-two problem. First, consider rate. Any time temperature is increased, the reaction kinetics increase. In this case, the salt will dissolve faster, eliminating choices C and D. An increase in temperature generally causes an increase in the solubility of solids in liquids. However, both solutions contain the same amount of MgSO₄ that does not exceed the maximum solubility at either temperature. Therefore, the concentrations of ions will be the same, eliminating choice B.

8. D The golden rule of solubility is “like dissolves like.” Potassium iodide is a salt held together by ionic forces and therefore comprised of charged ions. A salt will dissolve in a polar solvent better than a non-polar solvent. Propanol has a polar —OH group whereas propane is completely non-polar. Therefore, KI must have a smaller K_sp in propane than in propanol. The only answer that has a smaller K_sp value is choice D.

9. B Neutralizations are exothermic and form salt and water. The starting 500 mL solutions contain 6 moles each of NaOH and HCl. The final solution will be 1 L of 6 M NaCl(aq):

6 HCl(aq) + 6 NaOH(aq) → 6 NaCl(aq) + 6 H₂O(l)

Although the reaction quotient of NaCl in this resulting solution will slightly exceed K_sp:

Q = [Na⁺][Cl⁻] = [6][6] = 36

the temperature will be significantly increased, allowing more NaCl to dissolve (K_sp will increase with temperature), eliminating choice A. Choice C is eliminated because enthalpy significantly decreases as heat is given off in this exothermic reaction. Choice D is eliminated because NaCl is a neutral salt.

SOLUTIONS TO CHAPTER 10 PRACTICE PASSAGE

1. D NH₄⁺ is an acidic ion and CO₃²⁻ is a basic ion. Both could potentially affect the equilibrium described in Equation 3, so choice A seems unlikely. Although ammonium carbonate is a basic salt, eliminating choices B and C, this could not be determined without knowing the relative pK_b and pK_a values of NH₃ and HCO₃⁻ respectively. Given the rise in pH of groundwater and that CO₃²⁻ would likely have a common ion effect on the CaCO₃ solubility, less limestone would be expected to dissolve, leading to decreased formations in the cave.

2. C This question is best answered by Process of Elimination, because the answer is unexpected. CaCO₃ is an ionic compound with a melting point greater than 800°C, making choice A unlikely. If formation of stalactites and stalagmites were endothermic, increased temperature would favor their formation, eliminating choice B. Increased temperature decreases the concentration of dissolved gases in liquids, eliminating choice D. CaCO₃ is one of the exceptions to general solubility rules because its solubility in water actually decreases with increasing temperature. If less CaCO₃ gets dissolved, less will be available to precipitate in the cave as a stalactite or stalagmite.

3. C Calcium carbonate dissolves in water as follows:

CaCO₃(s) Ca²⁺ + CO₃²⁻

The K_sp defines the maximum solubility of a saturated solution. Solve the solubility expression for the maximum theoretical concentration of CO₃²⁻:

K_sp = [Ca²⁺][CO²⁻₃]

3.4 × 10⁻⁹ = [x][x]

x² = 34 × 10⁻¹⁰

x ≈ 6 × 10⁻⁵M

4. C A buffer must contain a conjugate acid-base pair. CO₃²⁻ is a basic ion so adding the conjugate acid, HCO₃⁻, would be required to form a buffer solution. NaHCO₃⁻ will most readily supply this.

5. B The carbonate ion is trigonal planar and the carbon atom is sp² hybridized:

With three total substituents, the carbon atom cannot be sp³ hybridized, eliminating choices A and D. Tetrahedral shapes require four substituents, eliminating choice C.

6. B According to the passage, increasing the amount of dissolved CaCO₃ that makes it to the ground/cave interface or maximizing the difference in ground and cave CO₂ levels will increase stalagmite formation. Choice A would decrease CaCO₃ solubility in groundwater by the common ion effect. Choice C would decrease CaCO₃ solubility in groundwater because the passage states acidic solutions dissolve CaCO₃. Choices B and D are opposite answers, which often means one is correct. The passage states that lower CO₂ levels in the cave compared to the leaking water lead to precipitation of CaCO₃. Therefore, choice D is eliminated and choice B is the best answer.