MCAT General Chemistry Review - Alexander Stone Macnow, MD 2019-2020
Electrochemistry
Electromotive Force and Thermodynamics
LEARNING GOALS
After Chapter 12.3, you will be able to:
· Apply the formula ΔG° = —RT ln Keq to calculations of Gibbs free energy or electromotive force
· Predict Ecell given reaction quotients and equilibrium constants
Throughout our discussion of electrochemistry and the different types of electrochemical cells, we have been making references to the spontaneity or nonspontaneity of the redox reactions housed in each of the different cell types. Let’s now look more formally at this topic by relating free energy to electromotive force (emf) and the concentrations of the oxidation—reduction reactants and products to the voltage of a cell at a given point in time.
GIBBS FREE ENERGY
By now, you should be familiar with the thermodynamic criterion for determining the spontaneity of a reaction: the change in Gibbs free energy, ΔG. This is the change in the amount of energy available in a chemical system to do work. In an electrochemical cell, the work done is dependent on the number of coulombs of charge transferred and the energy available. Thus, ΔG° and emf are related as follows:
ΔG° = —nFE°cell
Equation 12.4
where ΔG° is the standard change in free energy, n is the number of moles of electrons exchanged, F is the Faraday constant, and E°cell is the standard emf of the cell. Keep in mind that, if the Faraday constant is expressed in coulombs ![]() then ΔG° must be expressed in J, not kJ. Notice the similarity of this relationship to that expressed in the physics formula W = qΔV for the amount of work available or needed in the transport of a charge q across a potential difference ΔV: n × F is a charge, and E°cell is a voltage. This application in electrostatics is discussed in Chapter 5 of MCAT Physics and Math Review.
then ΔG° must be expressed in J, not kJ. Notice the similarity of this relationship to that expressed in the physics formula W = qΔV for the amount of work available or needed in the transport of a charge q across a potential difference ΔV: n × F is a charge, and E°cell is a voltage. This application in electrostatics is discussed in Chapter 5 of MCAT Physics and Math Review.
Bridge
Recall from Chapter 6 of MCAT General Chemistry Review that, if ΔG is positive, the reaction is nonspontaneous; if ΔG is negative, the reaction is spontaneous.
Note the significance of the negative sign on the right side of the equation. ΔG° and E°cell will always have opposite signs. Therefore, galvanic cells have negative ΔG° and positive E°cell values; electrolytic cells have positive ΔG° and negative E°cell values.
Example:
Determine the standard change in free energy of a cell with the following net reaction. (Note: The standard reduction potential of iron(III) is +0.77 V; the standard reduction potential of molecular chlorine is +1.36 V.)
2 Fe3+ (aq) + 2 Cl— (aq) → 2 Fe2+ (aq) + Cl2 (g)
Solution:
First, separate the reaction into the half-reactions:
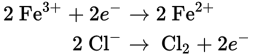
In this reaction, iron(III) is reduced and is the cathode, whereas Cl— is oxidized and is the anode. The reduction potential of chlorine is actually higher than that of iron(III); this means that the electrodes are serving the opposite role from their natural tendency, and the reaction is nonspontaneous. This is an electrolytic cell, and should have a negative emf value.
Now, determine the emf:
E°cell = E°red,cathode − E°red,anode = 0.77 V − 1.36 V = −0.59 V
Use the emf to determine the free energy change (note that as 2 electrons are transferred, n = 2):
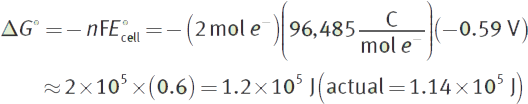
The free energy change is about +120 kJ, which represents a non-spontaneous reaction.
REACTION QUOTIENTS
So far, we have considered the calculation of a cell’s emf only under standard conditions. However, electrochemical cells may have ionic concentrations that deviate from 1 M. Also, for the concentration cell, the concentrations of the ions in the two compartments must be different for there to be a measurable voltage and current. Concentration and the emf of a cell are related: emf varies with the changing concentrations of the species in the cell. When conditions deviate from standard conditions, one can use the Nernst equation:
![]()
Equation 12.5
where Ecell is the emf of the cell under nonstandard conditions, E°cell is the emf of the cell under standard conditions, R is the ideal gas constant, T is the temperature in kelvins, n is the number of moles of electrons, F is the Faraday constant, and Q is the reaction quotient for the reaction at a given point in time. The following simplified version of the equation can be used, assuming T = 298 K:
![]()
Equation 12.6
This simplified version of the equation brings together R, T (298 K), and F, and converts the natural logarithm to the base-ten logarithm to make calculations easier.
MCAT Expertise
If the Nernst equation is needed on Test Day, stick with the log10 version because natural logarithm calculations get very tedious.
Remember that the reaction quotient, Q, for a general reaction aA + bB → cC + dD has the form:
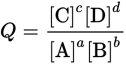
Equation 12.7
Although the expression for the reaction quotient Q has two terms for the concentrations of reactants and two terms for the concentrations of products, remember that only the species in solution are included. When considering the case of the Daniell cell, for example, only the concentrations of zinc and copper ions are considered:
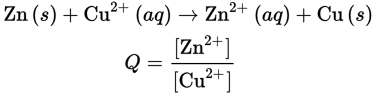
The emf of a cell can be measured with a voltmeter. A potentiometer is a kind of voltmeter that draws no current and gives a more accurate reading of the difference in potential between two electrodes.
Example:
Find the emf of a galvanic cell at 25°C based on the following standard reduction potentials:
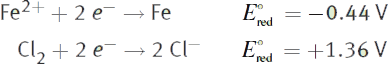
In this cell, [Fe2+] = 0.01 M and [Cl—] = 0.1 M.
Solution:
First, determine the standard cell potential. Because the chlorine half-reaction has a higher reduction potential, it will be the cathode. Iron will act as the anode. The standard cell potential is:
E°cell = E°red,cathode − E°red,anode = 1.36 V − (−0.44 V) = +1.80 V
Now, determine the net ionic equation. Remember that iron is being oxidized, so its reduction half-reaction in the question stem will have to be reversed. The net ionic equation is:
Fe + Cl2 → Fe2+ + 2 Cl—
From this equation, we can determine the value of the reaction quotient:
Q = [Fe2+][Cl—]2 = (0.01 M)(0.1 M)2 = 10—4
Now, plug into the Nernst equation, keeping in mind that two electrons are transferred (n = 2):
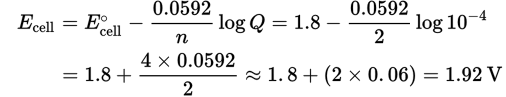
In this case, the cell actually has a higher voltage than it normally would due to the concentrations of ions present.
Bridge
While a mathematically rigorous equation, the Nernst equation has a powerful use in biochemistry for calculating resting and depolarized membrane potentials based on concentrations of ions. Its more extended version, the Goldman—Hodgkin—Katz equation, is discussed in Chapter 8 of MCAT Biochemistry Review. Equation 8.2 in that chapter looks slightly different than Equation 12.6 here. This is because the temperature is different (310 K rather than 298 K) and the units are different (mV instead of V).
EQUILIBRIA
As discussed in Chapter 7 of MCAT General Chemistry Review, ΔG° can also be determined in another manner:
ΔG° = —RT ln Keq
Equation 12.8
where R is the ideal gas constant, T is the absolute temperature, and Keq is the equilibrium constant for the reaction.
Combining the two expressions that solve for standard free energy change, we see that
ΔG° = —nFE°cell = —RT ln Keq
or
nFE°cell = RT ln Keq
By extension, if the values for n, T, and Keq are known, then E°cell for the reaction is easily calculated. On the MCAT, you will not be expected to calculate natural logarithm values in your head. That being said, these equations can still be tested but in a conceptual way.
MCAT Expertise
Whether it is log or ln, remember that a logarithm will be positive when equilibrium constants are greater than 1, negative when equilibrium constants are less than 1, and 0 when equilibrium constants are equal to 1.
Analysis of the equations shows us that, for redox reactions with equilibrium constants less than 1 (equilibrium state favors the reactants), the E°cell will be negative because the natural logarithm of any number between 0 and 1 is negative. These properties are characteristic of electrolytic cells, which house nonspontaneous oxidation—reduction reactions. Instead, if the equilibrium constant for the reaction is greater than 1 (equilibrium state favors the products), the E°cell will be positive because the natural logarithm of any number greater than 1 is positive. These properties are characteristic of galvanic cells, which house spontaneous oxidation—reduction reactions. If the equilibrium constant is equal to 1 (concentrations of the reactants and products are equal at equilibrium), the E°cell will be equal to zero. An easy way to remember this is that E°cell = 0 V for any concentration cell with equimolar concentrations in both half-cells because there is no net ionic equation (both half-cells contain the same ions).
Key Concept
If E°cell is positive, ln Keq is positive. This means that Keq must be greater than one and that the equilibrium lies to the right (products are favored).
Knowing the effects of concentration on equilibria, we can now derive the change in Gibbs free energy of an electrochemical cell with varying concentrations using the equation
ΔG = ΔG° + RT ln Q
Equation 12.9
where ΔG is the free energy change under nonstandard conditions, ΔG° is the free energy change under standard conditions (which can be determined from Equation 12.4 or Equation 12.8 above), R is the ideal gas constant, T is the temperature, and Q is the reaction quotient.
MCAT Concept Check 12.3:
Before you move on, assess your understanding of the material with these questions.
1. Fill in the table to show the relationships between the equilibrium constant, Gibbs free energy, and electromotive force (emf), assuming standard conditions:
|
Keq |
ΔG°: (+) or (−)? |
Reaction: Spontaneous or Nonspontaneous? |
E°cell: (+) or (−)? |
|
1.2 × 10—2 |
|||
|
2 × 102 |
|||
|
1 |
2. Given the following reaction quotients and equilibrium constants, determine the direction of the reaction and the sign of Ecell:
|
Q |
Keq |
Reaction Direction (Forward, Backward, or Equilibrium) |
Sign of Ecell |
|
10—3 |
10—2 |
||
|
10—2 |
1.1 |
||
|
1 |
1 |