Organic Chemistry I For Dummies, 2nd Edition (2014)

Chapter 6. Seeing in 3-D: Stereochemistry

IN THIS CHAPTER

Seeing molecules in three dimensions

Determining R and S stereochemistry

Shedding (plane-polarized) light on chiral molecules

Discovering diastereomers and Fischer projections

In this chapter, you look closely at molecules in three dimensions. Why should you care about the arrangements of atoms in three-dimensional space? Because nature does. Virtually all the compounds produced in nature — proteins, sugars, carbohydrates, DNA, and RNA, to name just a few — have atoms oriented in very specific ways in three-dimensional space.

Subtle differences in the way molecules are arranged in three-dimensions can be recognized, for instance, by your nose receptors. Limonene, for example, shown in Figure 6-1, can have two different three-dimensional configurations (solid wedges indicate a bond coming out of the plane of the paper; dashes indicate a bond going back into the paper). If the molecule is arranged in one configuration, it smells of oranges; arranged in the other configuration, it smells of lemons!

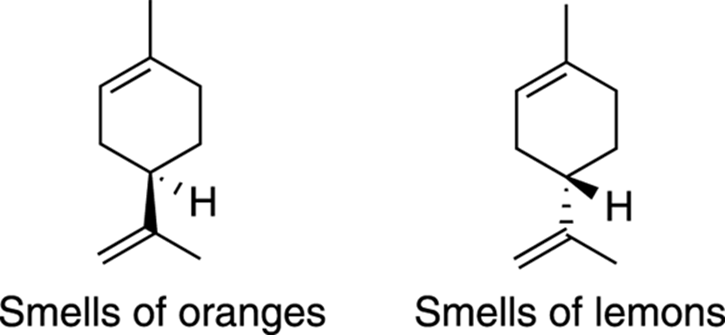
FIGURE 6-1: Two configurations of limonene.

This discrimination by your nose receptors (of molecules differing only in the orientation of atoms in three-dimensional space) is common in biological systems. Most drugs, in fact, are only active when they have a very specific three-dimensional configuration, while compounds with an identical structure but with different arrangements of the atoms in space are usually completely ineffective, or even harmful. (See the sidebar “The biological importance of stereochemistry: The thalidomide tragedy,” later in this chapter, for an example of such harmful drugs.) Because of this biological significance of the three-dimensionality of molecules, the study of stereochemistry (the way that molecules orient themselves in three-dimensional space) is very important, particularly in the pharmaceutical industry.

Drawing Molecules in 3-D

To be able to study stereochemistry, you need to be able to draw three-dimensional molecules on a two-dimensional piece of paper. When you draw molecules in three-dimensions, you typically use solid and dashed wedges. A solid wedge indicates a bond coming out of the plane of the piece of paper, and a dashed wedge indicates a bond going back into the paper. A regular line indicates a bond that’s in the same plane of the paper. When you want to draw an sp³ carbon atom (see Chapter 2) in three dimensions, you draw two bonds in the plane of the paper, one bond coming out of the plane of the paper, and one bond going back (behind the plane of the paper), in a tetrahedral arrangement (see Figure 6-2).

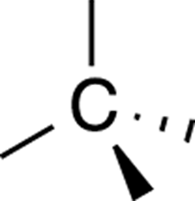
FIGURE 6-2: A tetrahedral arrangement.

Comparing Stereoisomers and Constitutional Isomers

The two different limonene molecules shown in Figure 6-1 are stereoisomers (molecules with the same atom connectivity but with different orientations of those atoms in space). Stereoisomers are different from constitutional isomers. Constitutional isomers are molecules with the same molecular formula but with atoms connected to each other in different ways (see Chapter 7).

Your hands, for example, are stereoisomers. On both hands, all your fingers are attached in the same way — thumb, index finger, middle finger, ring finger, and pinky, in that exact order. But although your hands have the same finger connectivity, your hands are not identical — they’re stereoisomers of each other. Try putting a right-handed glove on your left hand if you don’t believe me. If you happen to be an alien with one hand having a pinky where a thumb should be and a thumb where a pinky should be, then your hands would be constitutional isomers, because the connectivity of your fingers would be different.

Mirror Image Molecules: Enantiomers

Molecules that are nonsuperimposable mirror images of each other are called enantiomers. Your right hand is the enantiomer of your left hand because your hands are mirror images of each other (put your right hand up to a mirror, and you’ll see what looks like a left hand). Enantiomers cannot be superimposed onto each other, just as your right hand cannot be superimposed on your left hand. To translate this feature to structures, the compound shown in Figure 6-3 cannot be superimposed on its mirror image; if you slide the compound over its mirror image, the various parts of the two molecules won’t line up. You might try making the molecular models of the two enantiomers to prove to yourself that you can’t superimpose these enantiomers over each other — the atoms simply don’t align.

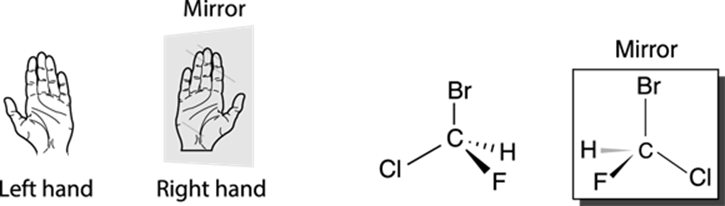
FIGURE 6-3: Enantiomers (mirror images).

If you really want to grasp stereochemistry, you need to mess around with molecular models. When you play with models, you get a feel for how stereochemistry works in your bones, not just in your head.

Molecules that are not superimposable on their mirror images (like the halogenated methane shown in Figure 6-3) are said to be chiral molecules (hard k sound, rhymes with viral). Conversely, molecules that can be superimposed on their mirror images are said to be achiral. Methane (shown in Figure 6-4) is an example of an achiral molecule. Methane is superimposable on its mirror image. That is, if you rotate the mirror image of methane, the atoms superimpose (or overlap) on the original molecule perfectly. Thus, methane doesn’t have an enantiomer because its mirror image is identical to itself.

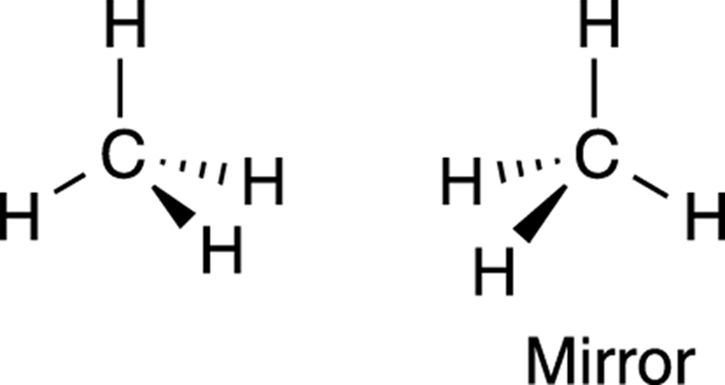
FIGURE 6-4: Methane, an achiral molecule.

Only chiral molecules have enantiomers.

Seeing Chiral Centers

How can you tell whether a molecule will be chiral or achiral without constructing the molecule’s mirror image and seeing if the two can be superimposed? Most often, chiral molecules contain at least one carbon atom with four nonidentical substituents. Such a carbon atom is called achiral center (or sometimes a stereogenic center), using organic-speak. Any molecule that contains a chiral center will be chiral (with one exception, discussed later). For example, the compound shown in Figure 6-5 contains a carbon atom with four nonidentical substituents; this carbon atom is a chiral center, and the molecule itself is chiral, because it’s nonsuperimposable on its mirror image.

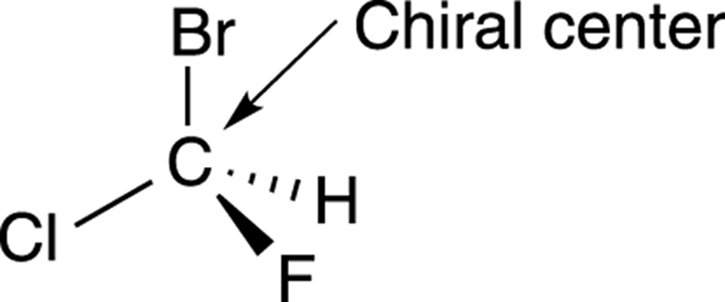
FIGURE 6-5: A chiral center.

You need to be able to quickly spot chiral centers in molecules. All straight-chain alkyl group carbons (CH₃ or CH₂ units) will not be chiral centers because these groups have two or more identical groups (the hydrogens) attached to the carbons. Neither will carbons on double or triple bonds be chiral centers because they can’t have bonds to four different groups. When looking at a molecule, look for carbons that are substituted with four different groups. See, for example, if you can spot the two chiral centers in the molecule shown in Figure 6-6.

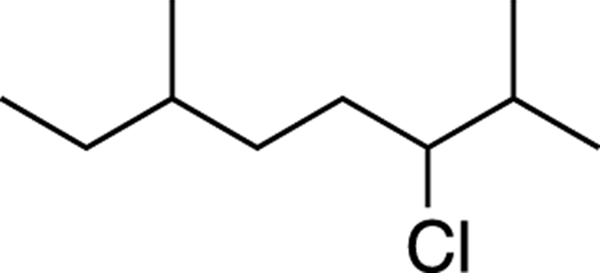
FIGURE 6-6: A molecule with two chiral centers.

Because not all CH₃ and CH₂ groups can be chiral centers, the molecule shown in Figure 6-5 has only three carbons that can be chiral centers. The two leftmost possibilities, identified in Figure 6-7, have four nonidentical groups and are chiral centers, but the one on the far right has two identical methyl (CH₃) groups and so is not a chiral center.

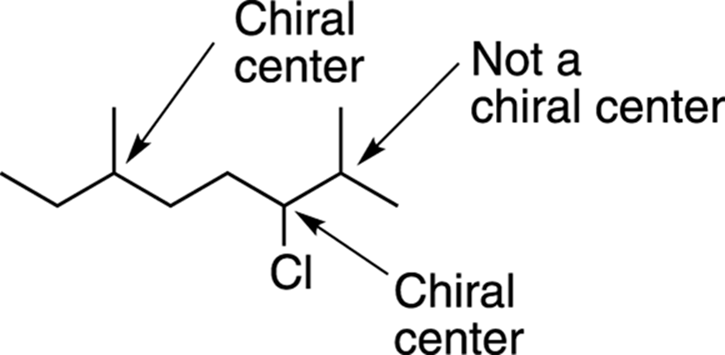
FIGURE 6-7: The chiral centers in a long molecule.

Assigning Configurations to Chiral Centers: The R/S Nomenclature

Any chiral center can have two possible configurations (just as a hand can have two configurations, either right or left), and these configurations are designated either R or S by convention (the letters R and S come from the Latin words for right and left, rectus and sinister). If a molecule has a chiral center that is designated R, the chiral center will be S in the molecule’s enantiomer.

You need to be able to assign whether a chiral center is R or S. To do so, you need to follow three steps:

1. Number each of the substituents on the chiral center carbon using the Cahn–Ingold–Prelog system.

This numbering scheme is conveniently the same one used in determining E/Z stereochemistry on double bonds, as described (in more detail) in Chapter 11. According to the Cahn–Ingold–Prelog prioritizing scheme, the highest priority goes to the substituent whose first atom has the highest atomic number. (For example, Br would be higher priority than Cl, because Br has a larger atomic number.) If the first atoms on two substituents are the same, you keep going down the chain until you reach a larger atom and the tie is broken.

2. After you’ve assigned priorities to each of the substituents, rotate the molecule so that the number-four priority substituent is oriented in the back.

3. Draw a curve from the first-priority substituent through the second-priority substituent and then through the third.

If the curve goes clockwise, the chiral center is designated R; if the curve goes counterclockwise, the chiral center is designated S.

Problem Solving: Determining R/S Configuration

To get the hang of applying R/S nomenclature to chiral centers, you need lots of practice. Try to determine the R/S stereochemistry of the chiral center in the molecule shown in Figure 6-8.

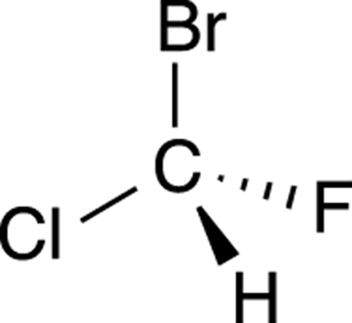
FIGURE 6-8: A chiral molecule.

Step 1: Prioritizing the substituents

The first step is to prioritize all the substituents from one to four. Bromine is the atom with the largest atomic number, so this substituent is given the highest priority; hydrogen has the smallest atomic number, so it’s given the lowest priority. Chlorine gets the number-two priority because it’s bigger than fluorine, which is given priority three. The priorities are shown in Figure 6-9.

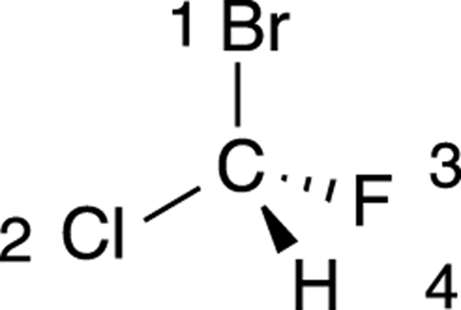
FIGURE 6-9: Prioritizing the substituents in a chiral center.

Hydrogen will always be given the lowest (fourth) priority.

Step 2: Putting the number-four substituent in the back

The next step is to rotate the molecule so that the number-four substituent is pointed toward the back, as shown in Figure 6-10. For many people, this is the most difficult step because to rotate the molecule requires visualizing the molecule in three dimensions.

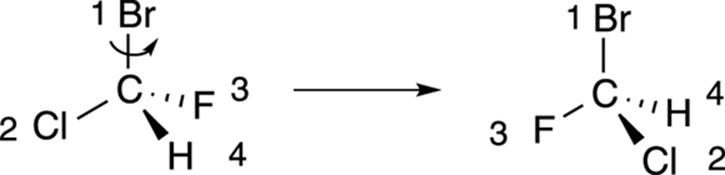
FIGURE 6-10: Rotating the molecule to put the fourth priority in the back.

If you’re not good at visualizing in three dimensions, you can use some tricks to put the number-four priority group in the back without having to mentally rotate the molecule in three-dimensional space.

First, swapping any two substituents changes the configuration — that is, if the chiral center was R before the swap, it becomes S after the swap (and vice versa). So, if you swap the number-four substituent with the substituent located in the back, as shown in Figure 6-11, the configuration of the chiral center switches. After you’ve made the switch to put the number-four priority substituent in the back, you could then go to Step 3 and determine the configuration, remembering that the actual configuration of that center is the opposite of the one determined.

FIGURE 6-11: Swapping two groups in a chiral center.

Or you could keep going, swapping two more positions. Swapping the positions of the first two substituents inverts the configuration, but swapping the remaining two substituents after you perform this operation reverts the configuration back to the one you started with, as shown inFigure 6-12. So, if you first swap the number-four substituent with the group in the back, and then swap the remaining two substituents, you get two inversions of the configuration, which amounts to a net retention of the configuration. (For example, if the chiral center starts R, and you invert two substituents, it becomes S; if you invert two more substituents, the configuration goes back to R.) Doing this double swap is an easy way of getting the number-four priority substituent into the back without doing mental rotations of the atoms.

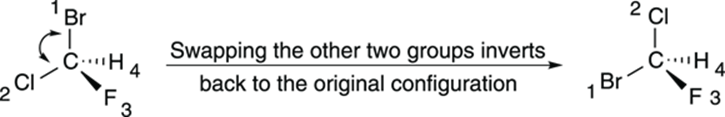
FIGURE 6-12: Swapping two more groups in a chiral center.

Swapping the positions of two substituents inverts the configuration.

Step 3: Drawing the curve

Now that the number-four priority substituent is in the back, you draw a curve from the first-priority substituent through the second-priority substituent, to the third-priority substituent. In this case, the curve goes clockwise, so the molecule has R stereochemistry, as shown in Figure 6-13.

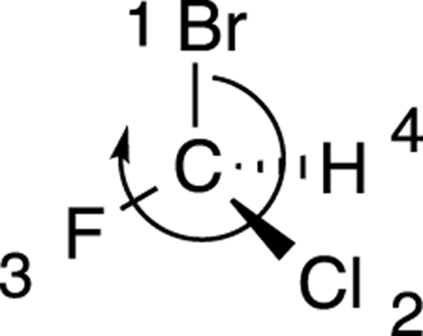
FIGURE 6-13: The R stereochemistry.

If the fourth-priority substituent is in front, you can just reverse the rules of the last step and cut out Step 3. With the number-four substituent in front, a clockwise curve from the first- to the third-priority substituents results in an S configuration; a counterclockwise curve would indicate an R configuration.

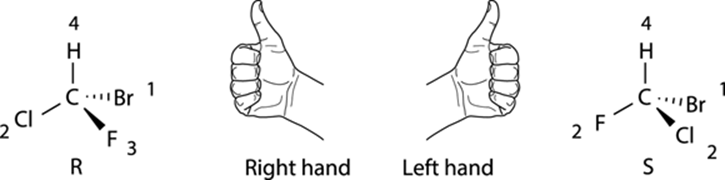
ALL THUMBS: AN ALTERNATIVE TECHNIQUE FOR ASSIGNING R AND S STEREOCHEMISTRY

A very convenient way to determine the R/S configuration of a chiral center is with the thumb technique. With this technique, shown in the accompanying figure, you point your thumb in the direction of the number-four priority substituent. If, with your thumb pointed toward the fourth-priority substituent, the fingers in your right hand can curl in the direction from the first- to second- to third-priority substituent in that order, the configuration is R; if you must use your left hand to get your fingers to curl from the first- to second- to third-priority substituent, then the configuration is S. The main advantage of this technique is that you don’t have to put the number-four priority substituent into the back; you just point your thumb in whatever direction the number-four priority substituent is facing.

The Consequences of Symmetry: Meso Compounds

Any molecule that contains a chiral center will be chiral, with one exception: Those molecules that contain a plane of symmetry will be achiral, regardless of whether the molecule has a chiral center. A plane of symmetry is a plane that cuts a molecule in half, yielding two halves that are mirror reflections of each other.

By definition, a molecule that’s not superimposable on its mirror image is a chiral molecule. Compounds that contain chiral centers are generally chiral, whereas molecules that have planes of symmetry are achiral and have structures that are identical to their mirror images. Molecules that contain chiral centers but are achiral as a result of having a plane of symmetry are called meso compounds, using organic-speak. For example, cis-dibromo cyclopentane (shown in Figure 6-14) is meso because a plane cuts the molecule into two halves that are reflections of each other. Trans-dibromo cyclopentane, however, is chiral because no plane splits the molecule into two mirror-image halves.

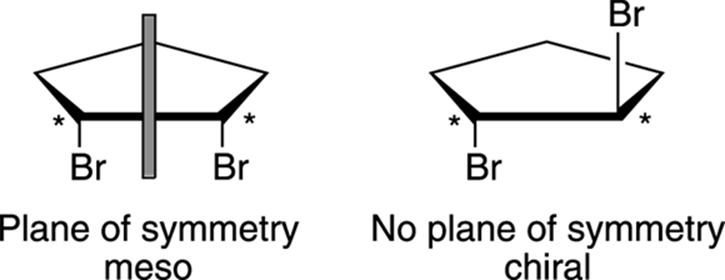
FIGURE 6-14: The plane of symmetry in meso compounds.

Look at the mirror images of these two molecules (shown in Figure 6-15) to prove this generality to yourself. Even though the cis compound has two chiral centers (indicated with asterisks), the molecule is achiral because the mirror image is identical to the original molecule (and is, therefore, superimposable on the original molecule). Molecules with planes of symmetry will always have superimposable mirror images and will be achiral. On the other hand, the trans stereoisomer has no plane of symmetry and is chiral.

FIGURE 6-15: The mirror images of achiral (meso) and chiral molecules.

Meso compounds are achiral.

In organic chemistry, you need to be able to spot planes of symmetry in molecules so you can determine whether a molecule with chiral centers will be chiral or meso. For example, can you spot the planes of symmetry in each of the meso compounds shown in Figure 6-16?

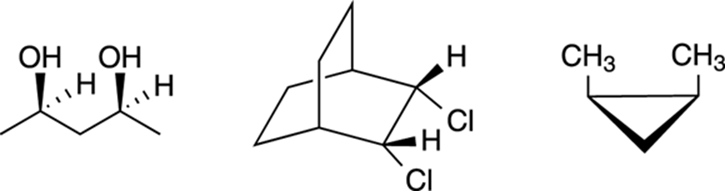
FIGURE 6-16: Some meso compounds.

Rotating Plane-Polarized Light

Enantiomers share nearly all physical properties with each other — they have the same boiling points, melting points, dipole moments, and all other properties, save one. Enantiomers rotate plane-polarized light in opposite directions. Light waves propagate in all directions, and plane-polarized light is simply light that has been filtered to allow only light propagating in one direction to pass through the filter (this is the way that polarized sunglasses work to block out light). When plane-polarized light is passed through a sample containing a chiral molecule, the light is rotated either to the right or to the left by a certain number of degrees (labeled α), as shown in Figure 6-17.

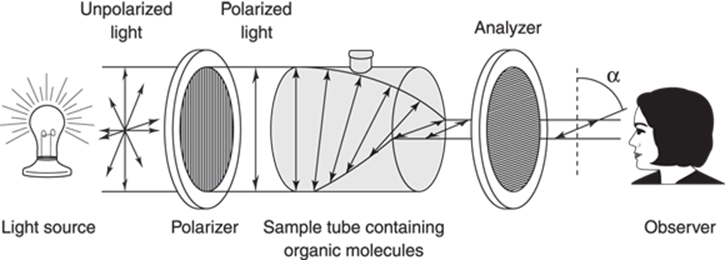
FIGURE 6-17: A polarimeter.

Only chiral molecules rotate plane-polarized light. The number of degrees that a chiral molecule rotates the light must be determined by experiment and is not something that you can figure out on your own. The direction of light rotation by a molecule is not something you can determine from looking at the structure of a molecule either (R or S designation does not tell you which way the light will be rotated). However, if you know that a chiral molecule rotates light by 30 degrees, then you know its enantiomer will rotate plane-polarized light by exactly –30 degrees (that is, 30 degrees in the opposite direction).

Enantiomers rotate plane-polarized light in equal and opposite directions.

If you mix two enantiomers in equal proportions, you get a racemic mixture — a 50/50 mix of enantiomers. Racemic mixtures do not rotate plane-polarized light. This is because half of the molecules in the mix rotate the light one direction, and the other half of the molecules rotate the light the other direction, resulting in a net rotation of zero. Such racemic mixtures are, therefore, said to be optically inactive, which means that they don’t rotate plane-polarized light.

Multiple Chiral Centers: Diastereomers

When only one chiral center exists in a molecule, the only possible stereoisomer is the enantiomer, the molecule’s mirror image. But when more than one chiral center is present in a molecule, you have the possibility of having stereoisomers that are not mirror images of each other. Such stereoisomers that are not mirror images are called diastereomers.

Typically, you can only have diastereomers when the molecule has two or more chiral centers.

The number of possible stereoisomers that a molecule can have is a function of 2ⁿ, where n is the number of chiral centers in the molecule. Therefore, a molecule with five chiral centers can have 2⁵ or 32 possible stereoisomers! As the number of chiral centers increases, the number of possible stereoisomers for that compound increases rapidly.

For example, the molecule shown in Figure 6-18 has two chiral centers.

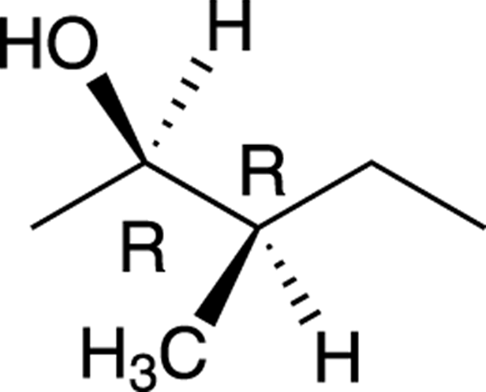
FIGURE 6-18: A molecule with two chiral centers.

Because this molecule has two chiral centers, this molecule can have a total of 2², or 4, possible stereoisomers, of which only one will be the enantiomer of the original molecule. Because both chiral centers in this molecule are of R configuration, the enantiomer of this molecule would have the S configuration for both chiral centers. All the stereoisomers of this molecule are shown in Figure 6-19. Those molecules that are not enantiomers of each other are diastereomers of each other.

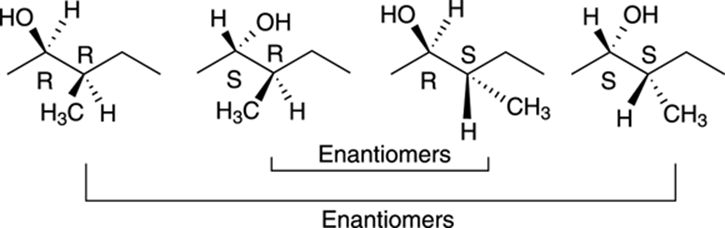
FIGURE 6-19: The four stereoisomers of a molecule with two chiral centers.

Representing 3-D Structures on Paper: Fischer Projections

The most convenient way of viewing molecules with more than one chiral center is with Fischer projections. A Fischer projection is a convenient two-dimensional drawing that represents a three-dimensional molecule. To make a Fischer projection, you view a chiral center so that two substituents are coming out of the plane at you, and two substituents are going back into the plane, as Figure 6-20 shows. Then the chiral center becomes a cross on the Fischer projection. Every cross on a Fischer projection is a chiral center.

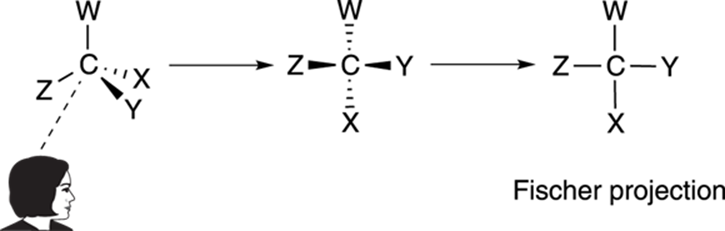
FIGURE 6-20: Creating a Fischer projection.

Rules for using Fischer projections

Fischer projections are convenient for comparing the stereochemistries of molecules that have many chiral centers. But these projections have their own sets of rules and conventions for how you can rotate and move them. The two main ways to rotate a Fischer projection are as follows:

· You can rotate a Fischer projection 180 degrees and retain the stereochemical configuration, but you cannot rotate a Fischer projection 90 degrees (see Figure 6-21).

· You can rotate any three substituents on a Fischer projection while holding one substituent fixed and retain the stereochemical configuration.

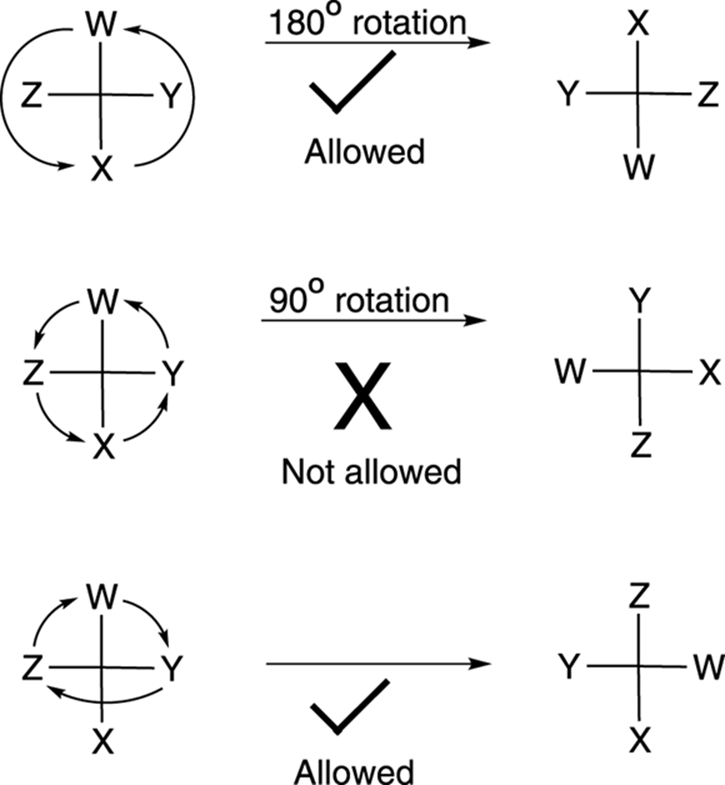
FIGURE 6-21: Working with Fischer projections.

Determining R/S configuration from a Fischer projection

Here’s how to determine the configuration of a chiral center drawn in a Fischer projection. First, you prioritize each of the substituents using the Cahn–Ingold–Prelog prioritizing scheme. (This is the same prioritizing scheme used in a previous section of this chapter and discussed in detail in Chapter 9.) Then, you put the fourth priority substituent on the top, and draw a curve from the first- to the second- to the third-priority substituent. If the curve goes clockwise, the configuration is R; if the curve goes counterclockwise, the configuration is S. To get the number-four priority substituent at the top of the Fischer projection, you have to use one of the two allowed moves diagramed in Figure 6-21. (You can make a 180-degree rotation, or you can hold one substituent fixed and rotate the other three.) Two examples of the determination of the configuration from Fischer projections are shown in Figure 6-22.

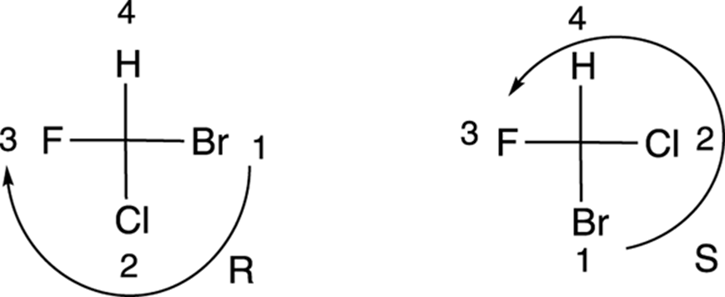
FIGURE 6-22: Determining R and S configurations from Fischer projections.

Seeing stereoisomerism with Fischer projections

One of the main advantages of Fischer projections is that you can easily see the relationships between stereoisomers. In other words, with a Fischer projection, you can quickly determine whether two stereoisomers are diastereomers or enantiomers. For example, the relationships between some stereoisomers of a molecule are shown in Figure 6-23. When you compare stereoisomers, you want to make sure that the tops and bottoms are lined up correctly. In other words, when comparing two Fischer projections, make sure that both projections have the same top and the same bottom, and that one isn’t upside-down (if one is upside-down, do an allowed 180-degree rotation). After the tops and bottoms are oriented correctly, you compare the directions of the substituents between the two molecules at every cross on the Fischer projection. A substituent that points to the left in a Fischer projection will point to the right in its enantiomer.

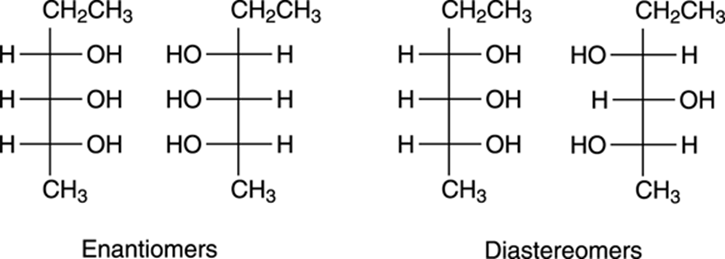
FIGURE 6-23: Seeing the relationships between stereoisomers in Fischer projections.

Spotting meso compounds with Fischer projections

Another convenient feature of Fischer projections is that you can often spot meso compounds more easily with Fischer projections than you can with molecules drawn out with dashes and wedges. With the Fischer projection, the symmetry of the molecule is easier to spot. An example of symmetry in a Fischer projection is shown in Figure 6-24.

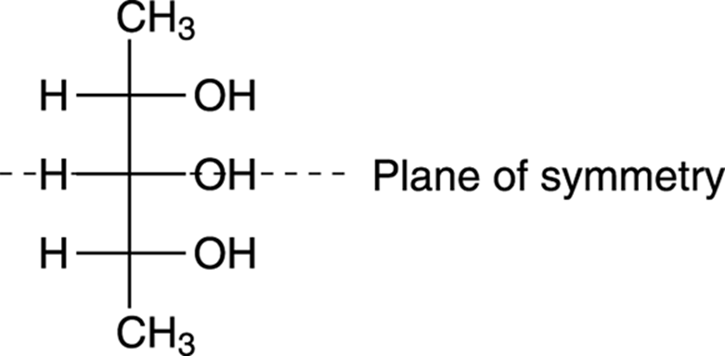
FIGURE 6-24: The Fischer projection of a meso compound.

Keeping the Jargon Straight

One of the most confusing aspects of stereochemistry is the massive amount of new terminology that you need to remember. So here’s a mini glossary of stereochemical terminology to keep you straight:

· Achiral molecule: An achiral molecule is one that can be superimposed over its mirror image; an achiral molecule is identical to its mirror image. Achiral molecules do not rotate plane-polarized light.

· Chiral center: Typically, for a molecule to be chiral, it must have at least one chiral center — a carbon with four nonequivalent groups. These chiral centers are assigned either R or S configuration. Any molecule that contains a chiral center will be chiral, unless the molecule has a plane of symmetry, in which case the molecule is achiral (and meso).

· Chiral molecule: A chiral molecule is one that cannot be superimposed over its mirror image. Chiral molecules rotate plane-polarized light.

· Diastereomer: Diastereomers are stereoisomers that are not mirror images of each other. For a molecule to have a diastereomer, it must typically have more than one chiral center.

· Enantiomer: Molecules that are mirror images of each other are called enantiomers.

· Meso compound: A meso compound is a molecule that contains a chiral center but is achiral as a result of having a plane of symmetry in the molecule.

· Optically active compound: An optically active compound (such as a pure solution of a single enantiomer of a molecule) has the ability to rotate plane-polarized light. The direction of light rotation is experimentally determined and is not predictable simply by looking at a structure.

· Racemic mixtures: A racemic mixture is a 50/50 mixture of two enantiomers. Racemic mixtures do not rotate plane-polarized light.

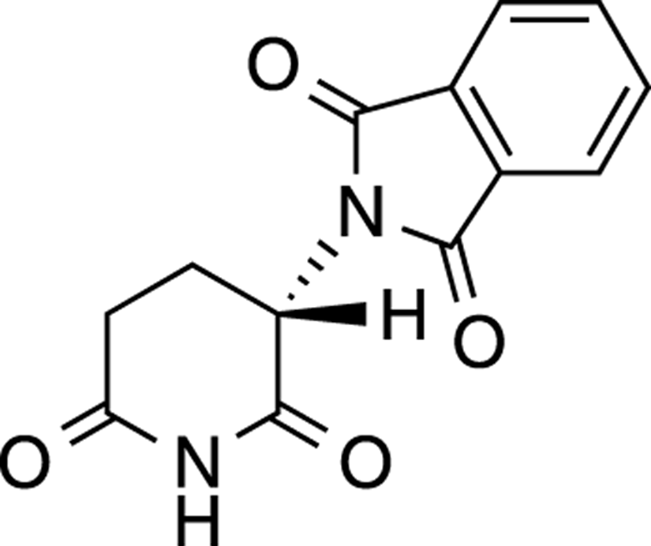
THE BIOLOGICAL IMPORTANCE OF STEREOCHEMISTRY: THE THALIDOMIDE TRAGEDY

Thalidomide, a chiral compound whose structure is shown in the accompanying figure, was a drug prescribed to pregnant women in Europe to counter the symptoms of morning sickness. Even though only one of the enantiomers of thalidomide actively worked against preventing morning sickness, the drug was prescribed as the racemic mixture (a 50/50 mix of both enantiomers).

Why was the drug dispensed as the racemic mixture rather than as the single active enantiomer? For practical reasons. Usually, selectively synthesizing one enantiomer over another is very difficult, and with most reactions that produce compounds with chiral centers, you get products that are racemic mixtures. Racemic mixtures are fiendishly difficult to separate because enantiomers share important physical properties. They have the same boiling points, so they can’t be separated by distillation; they have the same dipole moments and solubilities so they can’t be separated by recrystallization. Separating enantiomers is possible, but the task is often tedious and costly.

Unfortunately, while one enantiomer of thalidomide controlled the symptoms of morning sickness, the other enantiomer caused terrible side effects, including severe defects (like stunted limb growth) in the unborn children. The drug was pulled from the market when scientists discovered that these birth defects were caused by the drug.