Physical Chemistry Essentials - Hofmann A. 2018

Kinetics
6.5 Temperature Dependence of Reaction Rates

6.5.1 The Arrhenius Equation

We have previously discussed the temperature dependence of the equilibrium constant K (Sect. 2.2.6) which has been developed by van’t Hoff in 1884. Since the equilibrium constant is the ratio of the rate constants of the forward and the reverse reaction (Sect. 6.4.3, Eq. 6.33), it is reasonable to expect that both rate constants would be dependent on the temperature as well. This concept has been developed by Svante Arrhenius in 1889, who found that the temperature dependence of most reaction rates adheres to the Arrhenius equation (Arrhenius 1889a, 1889b):

(6.39)

Here, A is called the pre-exponential factor and E _a is the activation energy. When writing Eq. 6.39 in its logarithmic form

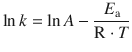
(6.40)

it becomes clear that a plot of lnk versus yields a line with slope ; such a plot is called an Arrhenius plot. The comparison of two reactions with different activation energies E _a shows that the higher the activation energy of a reaction, the stronger the reaction depends on the temperature. This is illustrated in Fig. 6.13, where the reaction with the higher activation energy is shown in blue. Due to the larger value of E _a, the slope of that line is steeper, and therefore the rate constant k varies stronger with temperature T.

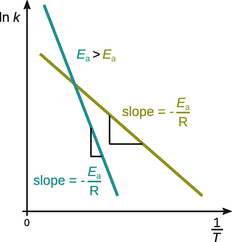
Fig. 6.13

Temperature dependence of the rate constant according to Arrhenius

If a reaction has an activation energy of E _a = 0, its rate constant does not depend on temperature. If negative activation energies are found, the rate constant decreases with increasing temperature—an indication of a complex reaction mechanism. There are also several cases, where the relationship between ln k and is not linear correlation; this means that the reaction does not behave according to the Arrhenius equation. Non-Arrhenius behaviour may be observed in explosions, enzyme reactions, heterogeneous catalysis and in cases of pre-equilibria.

As a general case, the activation energy at any temperature can be calculated according to

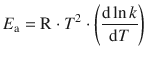
(6.41)

which applies to both Arrhenius and non-Arrhenius behaviour.

Since the variation of the rate constant k of a reaction directly affects the rate v, there is a practical implication of the Arrhenius equation: for many reactions at room temperature, the reaction rates double for every 10 K increase in temperature.

6.5.2 Interpretation of the Arrhenius Equation

When following the course of a reaction between two reactants A and B, the two molecules come into contact with each other, conformations change, and atoms are exchanged or discarded. These events are collectively summarised as the reaction coordinate. The potential energy along the reaction coordinate has a maximum value, and the corresponding atomic structure is called the activated complex (see Fig. 6.14). Here, the reactants are in a state of distortion where any further distortion will send them on the way to the products. This geometric configuration is thus called the transition state.

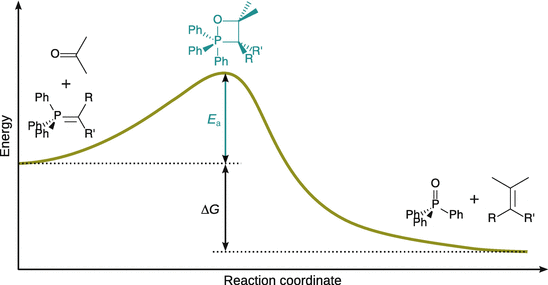
Fig. 6.14

Energy profile of a reaction without intermediate where the products have lower free energy than the reactants. E _a is the activation energy and ΔG is the free energy of the reaction. See further development of this concept in the transition state theory (Fig. 6.20)

The energy difference of the system between the start of the reaction and the activated complex is the activation energy E _a as introduced in the Arrhenius Equation (6.40). One can thus conclude that E _a is the minimum kinetic energy that the reactants must have in order to form products. The pre-exponential factor A is a measure of the rate with which collisions between molecules occur, irrespective of their energy. The product between the rate of collisions and the minimum kinetic energy required for reaction is thus the rate of successful collisions.

This fundamental concept and the exponential factor turn out to be essential components of the collision theory (Sect. 6.8) as well as the transition state theory (Sect. 6.11). Since the rate constant of a reaction is macroscopic parameter, the Arrhenius activation energy derived from Eq. 6.40 is also a macroscopic property, and should thus not be interpreted at the level of single molecules. E _a is an average energy determined from many individual collisions with varying collision parameters (collision angle, kinetic energy, internal energy); it is not simply a molecular threshold energy.