Physical Chemistry Essentials - Hofmann A. 2018
Kinetics
6.8 Collision Theory
After having discussed the overall dynamics of chemical reactions in the preceding chapters, we now want to have a closer look at what happens to molecules at the climax of reactions. We can certainly expect that extensive structural changes take place and energies are re-distributed among bonds.
The calculation of rates of such processes from first principles is very difficult, but a quantitative account of reaction rates can be given in terms of
✵ collision theory for gas-phase reactions
✵ diffusion theory for diffusion-controlled reactions in solution
✵ transition state theory for activation-controlled reactions in solution
6.8.1 Collision Theory for Bimolecular Gas-phase Reactions
In Sect. 6.5.2, we introduced the concept that products are only formed if the collision between two reactants is of sufficiently high energy; this required activation energy E a is described by the Arrhenius equation. An encounter of two reactants with less energy than E a will lead to separation without product formation.
This concept of collision can well be used to describe gas-phase reactions. For solution reactions, one can imagine the two reactants approaching by diffusion and then acquiring energy from their immediate surroundings while they are in contact.
We consider the following bimolecular elementary reaction
![]()
(6.61)
The rate of the reaction will be proportional to the rate of collisions, and thus to the mean speed of molecules, 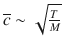 (cf. Sect. 5.1.1, Eq. 5.5). Also, the size of the reactants is an important parameter for successful collision; this is described by the cross-sectional area σ. (also called collisional cross-section). We thus obtain:
(cf. Sect. 5.1.1, Eq. 5.5). Also, the size of the reactants is an important parameter for successful collision; this is described by the cross-sectional area σ. (also called collisional cross-section). We thus obtain:
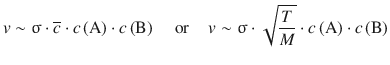
We have already established that not every collision will be reactive. Only those collisional encounters where the kinetic energy of the reactants exceeds the activation energy E a will lead to product formation. This is expressed by the Boltzmann factor: ![]() , leading to:
, leading to:
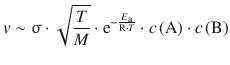
Still, despite considering the cross-sectional area σ, not every collision may lead to a reaction, since the reactants may have to collide in a particular orientation. This additional steric requirement is encoded in the factor P, so we obtain:
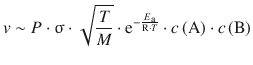
and from comparison with the rate law in Eq. 6.61, we derive the following relationship for the rate constant:
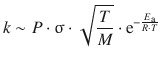
(6.62)
In words, Eq. 6.62 can be expressed as:

In the following, we will see that this concept describes all aspects of a successful collision and can be rigorously derived by the collision theory.
6.8.2 Collision Rates in Gases
In Sect. 5.1.1, we have briefly introduced the kinetic molecular theory of gases, and derived an expression for the speed of the molecules in a homogeneous system filled with gas. Extending this consideration to the more general case of two different gases A and B, the relative mean speed of two species can be derived from that theory:
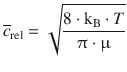
(6.63)
with ![]() being the reduced mass.
being the reduced mass.
The collision frequency Z AB between molecules of gas A and gas B can be derived as:
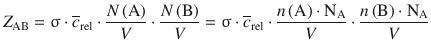
which yields
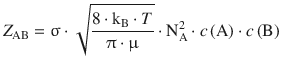
(6.64)
The collision cross-section σ is the area within which a projectile (A) must enter around the target (B) in order for a collision to occur. Figure 6.19 illustrates that, under the assumption of spherical particles, this requires a distance of the centres of gravity of the two particles of (r A + r B).
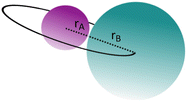
Fig. 6.19
Illustration of the collision cross-section of two spherical particles
The cross-section area is thus the area of a circle with radius (r A + r B):
![]()
(6.65)
The values of collision cross-sections of some select gases are given in 6.3. Using Eq. 6.64 and tabulated values of the collision cross-section, the collision frequency Z can be calculated. As an example, N2 under normal conditions (Tnormal = 298.15 K, c = 1 M) has a collision frequency of Z = 5·1034 m−3 s−1.
Table 6.3
Collision cross-section of select gases
|
Gas |
σ in nm2 |
Gas |
σ in nm2 |
H2 |
0.27 |
Ar |
0.36 |
He |
0.21 |
CH4 |
0.46 |
N2 |
0.43 |
CO2 |
0.52 |
O2 |
0.40 |
C2H4 |
0.64 |
Ne |
0.24 |
SO2 |
0.58 |
6.8.3 Energy Requirement for Successful Collision
We have previously established that for a successful collision to occur, the reactants need to have sufficient kinetic energy. The ratio of particles that possess energies ε i and ε j is given by the Boltzmann distribution (see Sect. 5.1.2):
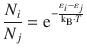
(5.7)
with Boltzmann’s constant kB = 1.381 10−23 J K−1
Note that the product of Boltzmann’s and Avogadro’s constant yields the gas constant kB·NA = R = 8.3144 J K−1 mol−1.
Here, ε denotes extensive energies measured in J, and E molar energies (intensive) measured in J mol−1.
From this equation it follows that the number of molecules that possess an energy E i ≥ E min is:
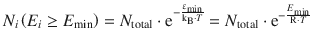
We can now combine the encounter (collision frequency Z AB) and the energy requirement (Boltzmann factor) to obtain a preliminary reaction rate:
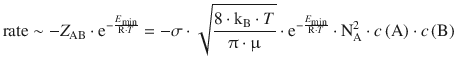
(6.66)
6.8.4 Steric Requirements
When comparing experimental data from gas phase reactions with the theory developed so far, it becomes obvious that there is agreement in some, but not all cases. Insights come from experiments using molecular beams, where it was observed that there can be three kinds of collisions:
✵ elastic (molecules separate again with total kinetic energy conserved)
✵ in-elastic (molecules separate again, but there is partial conversion of kinetic to potential energy)
✵ reactive (products are produced)
It thus seems appropriate to introduce a scaling factor (P) for the collision cross-section, that can be used to define the reactive cross-section σ*:
![]()
(6.67)
It is immediately obvious, that the steric factor P is indeed a scaling factor that describes the fraction of the cross-sectional area that delivers successful encounters:
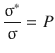
Intuitively, one would expect that the steric factor P assumes a maximum number of 1, and less than 1 for most instances. This is indeed the case, although exceptions are known. The reaction between K and Br2, for example, has a steric factor of P = 4.8, which indicates that this reaction proceeds by an unusual mechanism.
6.8.5 Combining the Collision Parameters
After having derived the individual components of molecular collision in the previous sections, we can now combine all of them into a theoretical reaction rate:
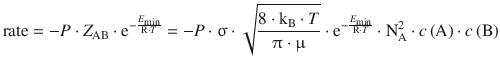
(6.68)
This agrees with the formal obtained for a bi-molecular reaction:

with the rate constant being a rate constant for the collision process
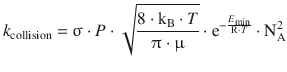
However, when we compare the units of the rate constant obtained from a bi-molecular reaction with the units for the collision rate constant, we find:
![]()
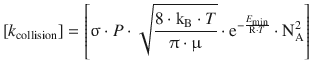
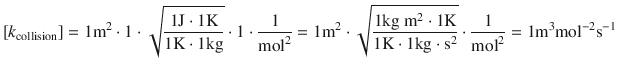
This shows that the units of the two rate constants are not the same, but they should! Both rate constants k reaction and k collision contain the units of ’volume per molar amount and time’, but due to the definition of the collision reaction in terms of molecules (rather than molar amounts), we now have to adjust for one additional molar amount unit. This is done by multiplying in Avogadro’s constant:
![]()
And we finally obtain the rate constant for a gas-phase bimolecular reaction (and substitute ’k reaction’ with ’k’):
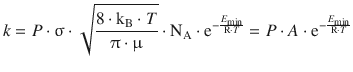
(6.69)
with the pre-exponential factor A being
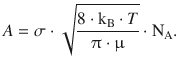
(6.70)
A describes the theoretical encounter rate minimum and the energy requirement for a successful collision of the two gas molecules based on collision theory. It may need to be adjusted for the reactive cross-section (σ*), which is done by multiplication with the steric factor P.
Estimation of the steric factor for a reaction
Consider the following gas-phase reaction
![]()
and determine the steric factor P at T = 628 K, given that the experimental pre-exponential factor is A exp = 1.24·106 dm3 mol−1 s−1.
In order to calculate the steric factor, we need to calculate the theoretical pre-exponential factor for the reaction (A), and compare it to the experimental value (A exp). The ratio between the two will be P, since A exp = P·A.
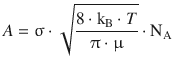
(6.70)
Collision cross-sections (see Table 6.3):
![]()
We approximate the cross-section as the average of the two:
![]()
For the mean speed of gas particles, we need the reduced mass:
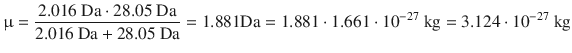
Therefore:
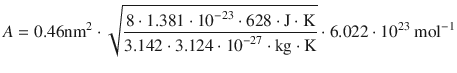
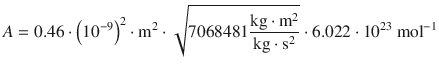
![]()
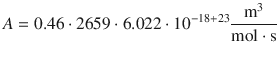
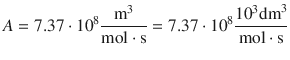
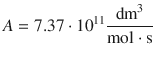
It follows:
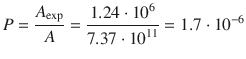
This low value for P is one reason, why catalysts are required to achieve hydration of ethane at reasonable rates.