Physical Chemistry Essentials - Hofmann A. 2018

Kinetics
6.11 Transition State Theory

In Sect. 6.5.2, we discussed molecular aspects of the Arrhenius equation and introduced the concept, that an activated complex needs to be formed that possesses the minimum energy ( activation energy E _a) required for the successful reaction.

With regards to terminology, the ’activated complex’ and the ’transition state’ are intimately linked, but not the same thing. The term ’activated complex’ describes a chemical assembly, i.e. a cluster of atoms. In contrast, the ’ transition state’ describes the nuclear and electronic configurations of the reactants which assume a form that transforms them into the products (see Fig. 6.20).

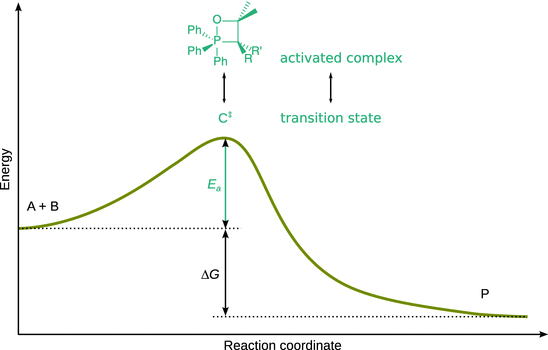
Fig. 6.20

Illustration of the transition state in an energy profile of a reaction. The ’activated complex’ describes the atomic assembly; the ’transition state’ comprises the entire configuration of that state, including nuclear and electronic configuration, and the internal motions. The energy profile is the same as seen earlier in Fig. 6.14

6.11.1 Formal Kinetics of the Activated Complex

The appearance of an activated species in the course of a reaction can be subjected to a formal kinetics treatment. Formation of the transition state C^‡ in the course of a reaction can be formulated as a rapid pre-equilibrium

If we consider, for illustration, a gas phase reaction, then we can describe the equilibrium constant as follows:

(6.76)

with the partial pressures p _i = R·T·c _i used instead of the concentrations c _i . Because the equilibrium constant K ^‡ has no unit, we need to multiply with the standard pressure p^—. This yields for the concentration of the activated complex:

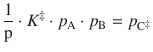
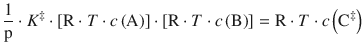
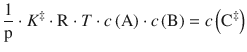
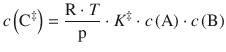
(6.77)

The overall reaction

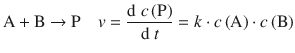
is a bi-molecular reaction and thus follows a second order rate law. Since the activated complex can decay to the products in a unimolecular reaction

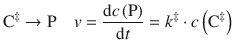
we can also formulate the rate law with respect to product formation based on the decay of the activated complex. For the rate of product formation we can therefore conclude:

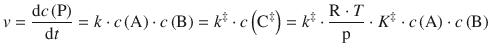
(6.78)

The above equation yields an expression of the macroscopic rate constant in terms of parameters that characterise the activated complex:

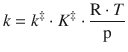
(6.79)

6.11.2 Internal Coordinates of the Activated Complex

In a more rigorous treatment of the activated complex that considers the internal motions (vibrations, rotations), it becomes apparent that not all of these motions ( degrees of freedom) send the complex into the way of the products. Since we now think of the activated complex (atomic arrangement) together with its internal motions, we will use the term ’transition state’ for the following discussion.

Based on the idea that not all internal motions lead to product formation, a transmission coefficient κ is introduced. The transmission coefficient describes the successful passage of the reactants through the transition state, on to the products. In the absence of specific information about a reaction, one assumes that κ = 1.

Within this concept, a modified equilibrium constant, , is introduced; it describes the transition state C^‡ with one vibrational mode being discarded. We have seen in the previous section, how the macroscopic 2nd-order rate constant is linked to the transition state:

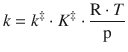
(6.79)

By taking into account the internal motions and the associate modified equilibrium constant, Henry Eyring, and, independently, Meredith Evans and Michael Polanyi, have further developed the theory of the activated complex to arrive at a description of the transition state (Evans and Polanyi 1935; Eyring 1935).

The Eyring equation

The 2nd-order rate constant can be developed as follows:

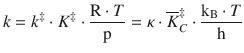
This expression is called the Eyring equation and links the macroscopic reaction kinetics and the molecular parameters of the reactants:

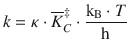
(6.80)

The factor describes a general frequency with respect to individual particles where h is the Planck constant. Notwithstanding the importance of this relationship, the required knowledge of the partition function of the transition state C^‡ (represented by ) makes its use in applied settings challenging. Internal modes of the activated complexes are difficult to access, since their characterisation (e.g. by means of spectroscopy) is rather complex.