Physical Chemistry Essentials - Hofmann A. 2018
The Fabric of Atoms
8.1 Properties of Light and Electrons
Several simple experiments indicate that neutral substances, i.e. such that possess no overall charge, are composed of charged particles whose individual charges balance each other. For example, if a salt is dissolved in water, the conductivity of the resulting solution is larger than that of pure water. Historically, the first findings in this context (Elster and Geitel 1882; Hertz 1887) were those showing that a metal can emit charged particles when either heated ( thermionic emission) or exposed to ultraviolet light ( photoelectric effect).
When the emitted charged particles in those experiments are accelerated by an electric field, they can even penetrate thin metal layers without being diverted from their initial direction of propagation (Lenard 1903). The emitted particles were thus termed cathode rays. Lenard therefore concluded that if atoms make up matter, then they cannot be solid particles that fill all the space occupied by matter. From those scattering experiments, the atomic radius was estimated to be approx 10−8 cm. The part of the atom that carries most of the mass (the nucleus) was estimated to possess a radius of approx 10−12 cm.
8.1.1 Charge and Mass of the Electron
Indeed, the charged particles emitted from metals upon exposure to high-energy light or heating are electrons, and the fact that they can be emitted by matter indicates that they are a constituting component of matter.
The charge of the electron was first estimated in a landmark experiment by Millikan who injected oil droplets into the slit between two horizontally arranged capacitor plates (Millikan 1913). The tiny charged droplets become charged and suspended against gravity. The electric field E provided by the capacitor plates, gives rise to an accelerating electrical force onto the charge Q which is given by
![]()
This accelerating force is either increased or lessened by the gravity, depending on whether the particles move upwards or downwards. The force on the particles due to gravity is calculated as per:
![]()
For a spherical particle, one obtains the following relationship between mass and radius:
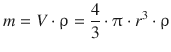
and thus
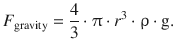
The total accelerating force on the charged particle in this experiment is thus
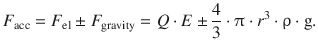
This is counteracted by the frictional force, as the particles are moving in air atmosphere. The frictional force is calculated according to Stokes for spherical particles that move with velocity v through medium of viscosity η:
![]()
A steady movement is observed when the two forces balance each other:
![]()
From this, the velocity of the moving particles can be calculated for the two cases, one where the particles move downwards (along the gravitational field) and one where they move upwards (against the gravitational field):
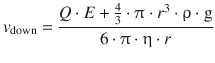
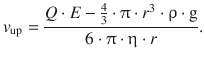
This constitutes two equations with two unknowns, Q and r; one of the unknown parameters can thus be calculated by measuring the velocities v up and v down for a sufficiently large number of particles. Since the oil droplets are macroscopic particles and might be multiply charged, the experimental values of Q are integer multiples of the elementary charge Q(e−) = e. This constant charge of the electron has been determined to be
![]()
(8.1)
In experiments with the cathode rays, it became apparent that the flight path of electrons emitted from the metal cathode can be altered by exposing the electron beam to an external magnetic field. This phenomenon was used by Thomson to quantitatively characterise the electron (Thomson 1897), allowing the calculation of its mass.
A charged particle with velocity v that is exposed to a magnetic field B experiences an acceleration by the Lorentz force, giving rise to a circular flight path. The Lorentz force acts as a centripetal force (directed towards the centre of the circle), and is balanced by the centrifugal force:
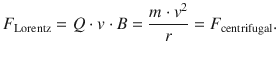
This yields an expression for the ratio between mass and charge of the particle, and in particular for the electron:
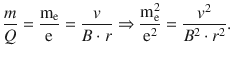
(8.2)
If the electrons in the cathode ray tube are accelerated by applying an external potential U, then we know that the electrons entering the magnetic field have a kinetic energy of
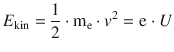
from which it follows that
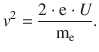
The above expression can be substituted into Eq. 8.2 which then yields:
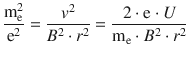
and thus
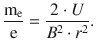
(8.3)
The mass-to-charge ratio of the electron can thus be obtained by knowledge of the external magnetic field strength B, the applied acceleration voltage U and the radius of the circular flight path of the electron. Importantly, as this relationship applies to any charged particle, its mass-to-charge ration m/Q can be obtained from the parameters B, U and r, when forcing the particle onto a circular flight path—a concept used for detectors in mass spectrometers.
With the known elementary charge e (Eq. 8.1), the mass of the electron has been determined to
![]()
(8.4)
8.1.2 The Wave Properties of Light
The corpuscular theory of light was put forward at the end of the sixteenth century by several philosophers and taken up by Isaac Newton (1704), explaining the optical phenomena known at the time. The Dutch mathematician and scientist Christiaan Huygens proposed in 1677 that light was a wave phenomenon (Huygens 1690); however, that theory only gained wider acceptance when the observation of interference could not be explained by the corpuscular theory.
The phenomenon of interference was demonstrated by experiments attributed to Thomas Young (Young 1802), where light from a coherent source passes two parallel slits and then observed behind the slits on a screen (Fig. 8.1). With just one open slit, a projection of the slit geometry is produced on the screen by a smooth distribution of light, as would be expected for a stream of particles. However, when both slits are open, a fringe-like pattern appears on the screen. This varying intensity of light after it passed the slits is called interference and is a phenomenon that cannot be explained by light behaving as particles, but rather waves.
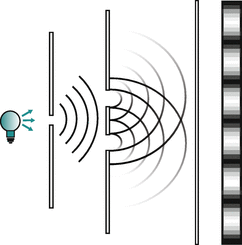
Fig. 8.1
Double-slit experiment to demonstrate interference
In 1871, James Clerk Maxwell formulated, based on ideas of Faraday and experiments by Hertz, the concept of light as an electromagnetic phenomenon, and light was then seen as a sole wave phenomenon.
Yet once again, these ideas were challenged by results obtained from black-body radiation. A black-body is a perfectly insulated enclosure that absorbs all incident electromagnetic radiation and only emits radiation through a hole made in its wall. The emitted radiation is independent of the chemical nature of the body and only depends on its temperature; it is hence called thermal radiation. The higher the temperature of the black-body, the more radiation it emits at every wavelength (see Fig. 8.2). For example, at room temperature, it emits radiation that is mostly in the infrared and invisible region of the spectrum. At higher temperatures, the emission of infrared light increases; it can be felt as heat and the body glows visibly red. At even higher temperatures (e.g. stars like the sun with a temperature of 5780 K at the surface), the body appears bright yellow or blue-white and emits significant amounts of short wavelength radiation, including UV and even X-rays.
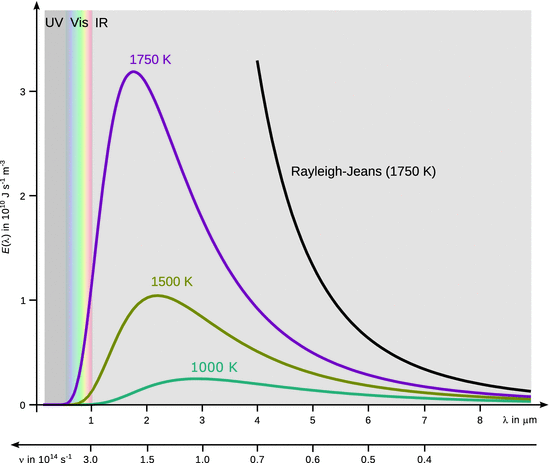
Fig. 8.2
Spectral flux density of the black-body
Rayleigh and Jeans proposed in 1900 that electrons at the surface of the black-body oscillate with a frequency ν, thus giving rise to electromagnetic radiation according to Maxwell’s theory of light for which the spectral flux density E(ν) can be calculated:
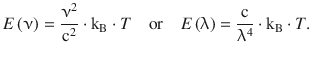
(8.5)
These expressions (known as the Rayleigh-Jeans law) describe the intensity of emitted radiation at a particular frequency ν or wavelength λ. This law predicts that the flux density increases with decreasing wavelength, and becomes infinite at very small wavelengths. As can be seen from Fig. 8.2, this predication is at odds with the experimentally observed spectral emission of the black-body. Whereas there is agreement at longer wavelengths, the experimental data shows an emission maximum at shorter wavelengths.
The issue arises from the assumption that surface electrons adopt a behaviour similar to linear oscillators, giving rise to the inner energy
![]()
It was Max Planck who realised that the energy of the oscillating electrons should be expressed as
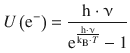
which then yields the Planck law:
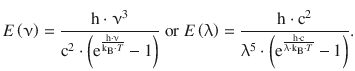
(8.6)
Planck’s law correctly predicts the radiation emitted by the black-body and introduces a constant h = 6.626176·10−34 J s which is called the Planck constant and possesses a finite value. The Planck constant is at the core of quantum theory:
Any action (= energy·time) of a natural event is an integer multiple of the quantum of action h. The smallest possible action is h.
This concept is part of a set of a distribution statistics for thermal equilibria. According to Planck, the energy is distributed among the atoms according to the temperature of the object. A few atoms have low energy, many have medium energy and a few have high energy. The large amount of atoms possessing medium energy increases as the temperature increases. Each atom can emit electromagnetic radiation. For very high frequencies ν, the energy needed to emit one quantum of energy is very large, and only a few atoms in the black-body have that much energy available, so only a few high-frequency quanta are radiated. It is much easier for atoms to emit low-energy (low frequency) radiation. In between the two extremes, however, there are many atoms that have enough energy to emit radiation of moderate energy. These add up to produce the peak in the emission curve of the black-body. This peak shifts to higher frequencies for bodies at higher temperature, since there are more individual atoms that possess higher energy.
8.1.3 The Photoelectric Effect
When light of sufficient energy is hitting onto a metal plate, electrons (now called photoelectrons) are released from the metal that possess a certain kinetic energy ![]() . This energy can be measured by clamping the metal plate against another electrode and apply an electric field that opposes the stream of photoelectrons. By varying the electric potential such that the stream (= current I) of photoelectrons reduces to zero (U 0), one can measure the maximum kinetic energy of the photoelectrons:
. This energy can be measured by clamping the metal plate against another electrode and apply an electric field that opposes the stream of photoelectrons. By varying the electric potential such that the stream (= current I) of photoelectrons reduces to zero (U 0), one can measure the maximum kinetic energy of the photoelectrons:
![]()
Since the photoelectrons are released as a result of the incident light, the wave theory of light predicts that the kinetic energy of the photoelectrons should vary with the intensity of the incoming light wave whose impulse is being transferred onto the electrons. However, whereas more intense light causes a larger current of photoelectrons, the maximum kinetic energy of those electrons, measured via the potential U 0, remains constant.
If the energy (h·ν) of the incident light is increased by shining light of higher frequency ν (shorter wavelength λ) onto the metal electrode, the kinetic energy of the photoelectrons increases in a linear fashion (Fig. 8.3). If the metal electrode is changed to a different material, the same type of relationship is observed, but the line is shifted parallel along the x-axis. This relationship can be mathematically formulate as:
![]()
and multiplied with the elementary charge e to obtain the same relationship in terms of energies:
![]()
(8.7)
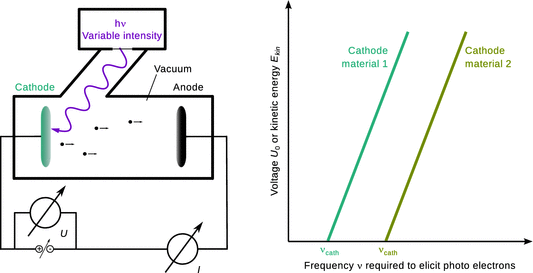
Fig. 8.3
The photoelectric effect. Left: Schematics of an apparatus to measure the kinetic energy of photoelectrons. Right: The higher the energy of the incident photons (i.e. the higher the frequency ν), the higher the kinetic energy (measured via the potential U 0 required to reduce the current to zero) of the photoelectrons emitted by the cathode. Different cathode materials show the same relationship, but the energy of the incoming photons required to elicit photoelectrons is different
The first factor on the right hand side of Eq. 8.7 is again a constant and turns out to be the Planck constant h. Re-arrangement of this equation then yields Einstein’s frequency law (Einstein 1905) which earned him the Nobel prize in 1921:
![]()
(8.8)
These results from the photoelectron experiments do not agree with the wave theory of light. Instead, Eq. 8.8 suggests that light propagates in the form individual quanta that travel with the speed of light c. These light quanta are called photons which have an energy
![]()
(8.9)
and can thus be likened to corpuscular radiation. The term h·νcath on the right hand side of Eq. 8.8 is dependent on the material of the photoelectrode and constitutes the work required to remove an electron from the solid matter.
8.1.4 The Dual Nature of Light
The photoeffect is proof that light, besides its wave behaviour, also possesses corpuscular characteristics. Emission of photoelectrons is only possible if the incoming light possess an energy larger than the work required to release an electron from the solid. The kinetic energy of photoelectrons cannot be changed by the intensity of the incoming light, but only by changing its energy. The intensity only affects the current (i.e. number) of released photoelectrons.
The interference experiments described in Sect. 8.1.3 (Fig. 8.1), can be modified such as to measure photons as they pass through the slits. These measurements show that each photon passes through one slit as it would be expected for a particle. Furthermore, the photons detected on the screen behind the slits are always detected at discrete points, demonstrating again behaviour of a single particle. Only the varying density of these hits (i.e. a distribution counted over many individual events) gives rise to the interference pattern (see also the discussion of electron diffraction in the next section).
8.1.5 The Dual Nature of the Electron
In Sect. 8.1.1, we discussed the corpuscular characteristics of the electron. If a thin layer of solid polycrystalline material is subjected to an incident electron beam (Fig. 8.4), then the corpuscular theory would predict a single point of incident on the detector. However, diffraction rings are observed instead, similar to the observation made in X-ray diffraction experiments (see Sect. 13.5.2).
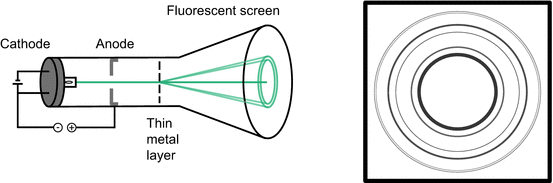
Fig. 8.4
Electrons accelerated in a cathode ray tube onto a thin metal layer show electron diffraction on the fluorescent screen
The diffraction of electrons cannot be explained by the corpuscular theory as it is an interference phenomenon that requires waves. Just as light, the electron therefore also possesses properties of a particle and a wave.
In the cathode ray tube, it is possible to accelerate the electrons by varying the potential difference that gives rise to the electric field experienced by the electrons. Experimentally, it can be shown that the wavelength of the electrons is indirectly proportional to their momentum:
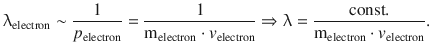
This important relationship is known as the DeBroglie relationship and links the corpuscular property (momentum) of the electron with its wave property (wavelength). The proportionality constant is thus of pivotal importance as it is the very factor that enables this conversion. It will not come as a big surprise that this constant is the Planck constant h, which renders the DeBroglie relationship as
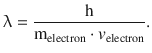
(8.10)
Optical resolution and electron microscopes
The wave properties of electrons are the basis for the important practical application in electron microscopes. The resolving power of optical systems defines the ability of an imaging device to separate points that are located at a small distance. The minimum resolvable distance is often called (angular) resolution. Physically, this is determined by the Rayleigh criterion which states that two point-like light sources are just resolved, when the main diffraction maximum of one image coincides with the first minimum of the other. Any greater distance between the two point sources means they are well resolved; any smaller distance makes the two points non-resolvable. In terms of a circular aperture, this leads to the equation
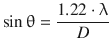
where θ is the angular resolution, λ the wavelength of light used to image and D the diameter of the aperture of the lens system; the factor of 1.22 is derived from the Bessel function of first order first kind, divided by π (J 1/π = 1.22). It is obvious from above equation that the resolution (θ) will assume smaller values (i.e. “increase”), as the wavelength of the light used becomes smaller.
The human eyes are sensitive to wavelengths of light in the range of 750 nm to 400 nm; the maximum resolution is equivalent to an object size at the order of 0.1 mm. With the help of optics, the light microscope (operating in the same wavelength range) can achieve a resolution of about 200 nm. In electron microscopes, the wave behaviour of electrons yields radiation of a wavelength of about 0.1 Å and contemporary instruments achieve a resolution of about 1—2 Å.
The dualism raises the question of what individual objects, such as a single electron is at a particular point in time. Is it simultaneously a particle and wave? We therefore consider again an electron beam produced in an evacuated tube (Fig. 8.5).
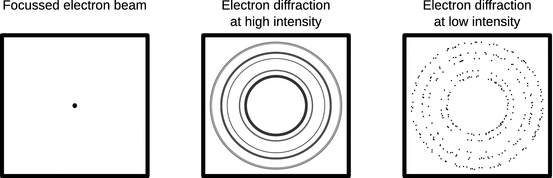
Fig. 8.5
Electron diffraction experiments. See main text for discussion
If there is no solid material in the way of the electron beam, it can be focussed and appears as a single intense spot on the detector (Fig. 8.5, left panel). When the beam penetrates a thin sample of solid polycrystalline matter, a diffraction image appears on the detector that is reminiscent of those obtained with X-rays as mentioned above (Fig. 8.5 centre panel). If one now lowers the intensity of the electron beam, the intensity of the diffraction rings gradually decreases. However, when the intensity is lowered such that it is no longer a beam of electrons, but rather a stream of individual electrons hitting the solid sample, the diffraction rings disappear from the detector and only individual and independent spots of incidence are recorded (Fig. 8.5 right panel). When observed over a long time, the individual spots of incidence will compose the original diffraction image.
If the electrons indeed possessed wave properties throughout, the complete diffraction image in above experiment should have been visible at all times. These observations suggest, that in this type of experiment the wave properties only exist for statistics of many particles.
8.1.6 The Wave-Particle Dualism
In the previous sections, we came to appreciate that light as well as electrons possess characteristics of particles as well as waves. With the characteristic properties of waves being the wavelength λ, and the characteristic properties of moving particles being their momentum p, the pivotal relationship of the wave-particle dualism is the DeBroglie relationship:
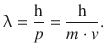
(8.10)
For photons, the corpuscular energy is E = m·c2, so their momentum is p = m·c. With Eq. 8.9 it then follows that
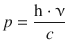
and substitution in Eq. 8.10 then leads to the relationship between wavelength λ and frequency ν of photons:
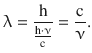
(8.11)
Whereas these discoveries were originally made with light and electrons, it has been shown by using atomic and molecular rays that the wave-particle dualism also exists for larger and thus heavier particles. From the DeBroglie relationship 8.10 it is obvious that the wavelengths of heavy particle rays have very small wavelengths (due to the high mass as compared to electrons or photons) and these small wavelengths are very difficult to detect. The largest entities for which the wave-particle dualism has been experimentally tested were molecules with some 800 atoms and a total mass of approx. 10,000 Da (Eibenberger et al. 2013).
In the previous sections, we discussed the interference of light and the diffraction of electrons. If we describe the beam of photons or electrons as a stream of particles, then a measure for the intensity of the beam is the number of particles passing a tiny volume slice per time. If we describe the beam as a wave characterised by an amplitude Ψ, then the intensity of the beam in a small volume element is proportional to the squared amplitude, Ψ2.
In the case of the low intensity beam in above diffraction experiment (Fig. 8.5 right panel), we can not predict where an electron will be hitting the detector area. However, the probability will be high in those regions where a strong diffraction ring is located (known from the experiment that worked with the intense electron beam). Notably, the intensity of a diffraction ring is a function of the intensity (= squared amplitude) of the electron wave. The squared amplitude Ψ2 therefore is a measure of the probability to find an electron at a particular location (in this case on the detector area).
In this particular experiment, we can determine with confidence the kinetic energy of the electrons forming the beam; it is given by the electric potential applied to accelerate the electrons in the tube. We thus know with great certainty what the momentum p = m·v and thus the wavelength λ of the electron beam is. However, we cannot be certain where exactly an electron will hit the detector, the exact three-dimensional coordinates (x, y, z) are unknown.
This observation illustrates Heisenberg’s uncertainty relationship which states that
The more precise the momentum of a particle is defined, the less certainty there is about the particle’s location. And vice versa, the more precisely the location of a particle is known, the less certainty there is about its momentum.
Wave packets
For (heavy) particle waves, neither the wavelength λ, nor the frequency ν can be measured. The same is true for the phase velocity which is the rate at which the phase of the wave propagates in space (note: for light, the phase velocity is c and can be measured).
If waves of slightly differing wavelengths are superimposed, this yields a so-called wave packet (Fig. 8.6). In such packets, oscillations of the individual constituting waves amplify each other in some areas, and they cancel the amplitudes in other areas. The wave packet as whole travels through space with the group velocity.
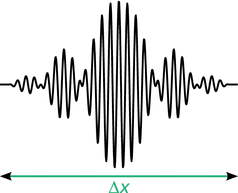
Fig. 8.6
Illustration of a wave packet
The propagation of an electron beam—when considered as a wave—may thus be described as a travelling wave packet, where the areas of large amplitudes indicate a high probability of the location of an electron and the areas of low or zero amplitude indicate low or zero probability of finding an electron.
A wave packet that describes a moving particle requires a particular width Δx. If this width is very small, the location of the particle is well defined. However, in order to obtain a very thin wave packet, the superposition of many waves of varying wavelengths λ is required; the wavelength range Δλ is large. In contrast, if only few waves with differing wavelengths are superimposed (Δλ is small), the resulting wave packet is rather broad (Δx is large), therefore giving a considerable ambiguity as to the actual location of the particle. Earle Hesse Kennard then derived the inequality of the product of the two distributions Δx and Δλ:
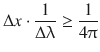
from which one derives with the DeBroglie relationship 8.10:
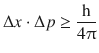
(8.12)
which summarises Heisenberg’s uncertainty relationship in a numerical fashion.
Importantly, this quantum mechanical principle does not violate observations made with macroscopic objects. For heavy particles, which are the subject of classical mechanics, the mass m is orders of magnitudes larger than for (sub)atomic particles. If we replace the momentum p by the product of mass and velocity, we obtain:
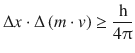
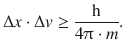
(8.13)
In formula 8.13, the right side of the inequality assumes values near zero in the case of heavy particles due to the large numerical value of their mass. This means that the uncertainty on the left hand side of may take very small values or indeed zero. In other words, there is virtually no uncertainty as to the location (Δx) and velocity (Δv) of the particle.
Since we have recognised that the wave-like behaviour of electrons and light can only be established through a distribution of many individual events, we can understand that it is not possible to track the path of an individual wave, for example behind the slits in the interference experiment in Fig. 8.1. Any screen or detector would only ever measure the absorption of a particle like-photon at a discrete point. The act of observation therefore affects the result obtained with the measurement. It is not possible to observe the particle and wave aspects of these beams simultaneously. This phenomenon is termed the complementarity principle.