Physical Chemistry Essentials - Hofmann A. 2018
Quantum Mechanics of Simple Systems
9.3 The Harmonic Oscillator
In the previous models considering the rigid rotor, we did not require to pay particular attention to the potential energy, as the distance between the two masses m 1 and m 2 does not change. The potential energy of the rigid rotor is therefore zero. If we consider a di-atomic molecule, however, the distance between the two atoms is not constant, due to the molecular vibration which causes the inter-atomic distance to fluctuate around an equilibrium distance.
From classical mechanics, we remember that the elongation of a mass m suspended by a spring leads to an oscillation behaviour (see Fig. 9.2) which is described by Hook's law:
![]()
(9.30)
where the force of elongation F is proportional to the elongation distance x and related by the spring constant k.
Since the force is the first derivative of the potential energy
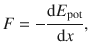
(9.31)
it becomes clear that
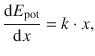
(9.32)
which can be integrated to allow calculation of a numerical value of the potential energy V and results in a parabolic dependence of the potential energy from the elongation distance x (Fig. 9.9):
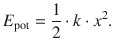
(9.33)

Fig. 9.9
Potential energy of the harmonic oscillator
The frequency of vibrational oscillation of a di-atomic molecule can also be derived from the classical mechanics, if the reduced mass μ is used to describe the two connected masses m 1 and m 2:
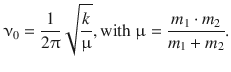
(9.34)
For the quantum mechanical treatment of the vibration of a di-atomic molecule, we need to use the potential energy (Eq. 9.33), as well as the reduced mass μ when compiling the Schrödinger equation:
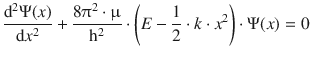
(9.35)
Due to some advanced mathematics required to solve this equation, we refrain from a rigorous discussion and appreciate that solutions for Eq. 9.35 can be found whereby the wave functions Ψ n take the form of
![]()
(9.36)
introducing the new quantum number, v. The constant β is comprised of the mechanical properties of the di-atomic molecule (reduced mass μ and spring constant k), and N v is a normalisation factor. Their definitions are:
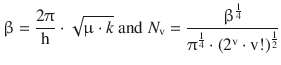
(9.37)
The function H v(x) is a potential development series; the wave functions for the first five quantum numbers (v = 0, 1 … , 4) are summarised in Table 9.1 and graphically illustrated in Fig. 9.10.
Table 9.1
Solutions to the Schrödinger Eq. 9.35 for the first five quantum numbers v
v = 0 |
|
v = 1 |
|
v = 2 |
|
v = 3 |
|
v = 4 |
|
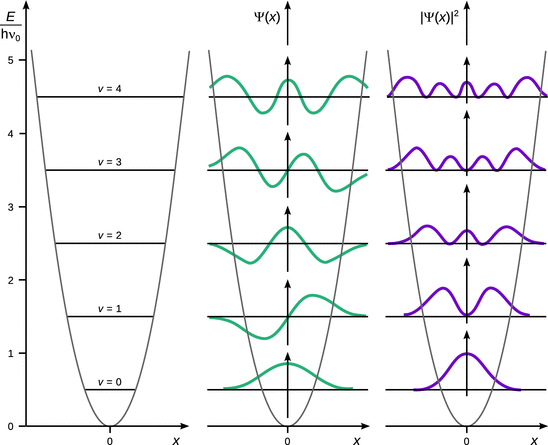
Fig. 9.10
Allowed energy levels (left), wave functions (centre) and probability density (right) of the harmonic oscillator
As observed in the previous systems, the harmonic oscillator assumes discrete energy levels (Fig. 9.10), which are a function of the quantum number v:
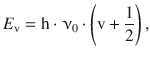
(9.38)
where ν0 is the frequency as defined in Eq. 9.34. Notably, the lowest energy state achieved at the quantum number v = 0 still comprises the zero-point energy of
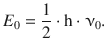
(9.39)
Figure 9.10 (right) illustrates that the probability of finding the particle varies strongly with the location x, and this variation, in turn, differs with the quantum number v. Importantly, the quantum mechanical results also show that the particle can exist outside the region enclosed by the parabolic potential wall.