Physical Chemistry Essentials - Hofmann A. 2018

Quantum Theory of Atoms
10.2 The Quantum Numbers

The solution of the Schrödinger equation for the hydrogen atom provided three quantum numbers, n, l and m. Importantly, the energy of the electron of atomic hydrogen only depended on the primary quantum number n (Eq. 10.9) and a degeneracy of n ² (Eq. 10.8). These quantum mechanical findings are in agreement with the energy levels in Bohr's atomic model as well as the atomic spectrum of hydrogen.

However, when observing the atomic spectrum of hydrogen in the presence of an outside magnetic field, the degeneracy of energy levels disappears resulting in splitting of individual spectral lines. This effect was discovered in 1896 by the Dutch physicist Pieter Zeeman and is thus called the Zeeman effect.

10.2.1 The Quantum Numbers of the Orbital Angular Momentum and Magnetic Momentum

The discussion in the previous sections showed, that the type of rotation of an electron around the atomic nucleus is described by the spherical harmonics Y _l,m (θ,ϕ) (Eq. 9.28) as described for the rigid rotor with space-free axis. Therefore, the quantum number l characterises the orbital angular momentum of the orbiting electron. The orbital angular momentum is a vector and thus has a length and a direction. Notably, electrons in s orbitals (l = 0) possess no orbital angular momentum, but electrons in other orbitals (p, d, f, …) do.

The quantum number m becomes important, when the electron rotates around a fixed axis, for example, when the atom is brought into a magnetic field. The quantum number m (or m _l ) is thus called the magnetic quantum number and determines the orientation of the orbital angular momentum in space.

Since an electron orbiting the atomic nucleus is a moving moving charge, it represents an electrical current, which, in turn, induces a magnetic field. In the presence of an outside magnetic field, the magnetic field of the orbiting electron is aligned with the external magnetic field. More specifically, the orbital that the electron is in is aligned by the outside field. For illustration, we consider the d orbital where l = 2 and |m _l | ≤ l (see Eq. 9.27), so that there are five (2·l + 1) degenerate energy levels. Since all five levels possess the same energy, the orbital angular momentum has no preferred orientation. This changes when an external magnetic field is applied. The five energy levels of the d orbital are no longer degenerate and split into discrete levels that also enforce particular directions of the orbital angular momentum —this phenomenon is known as space quantisation (Fig. 10.7). The value of the orbital angular momentum (the length of the vector  ) is different for the different subshells and given by:

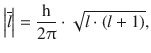
(10.14)

so for l = 2, this yields a value of . In the presence of a magnetic field , the component parallel to then depends on the magnetic quantum number m _l :

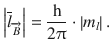
(10.15)

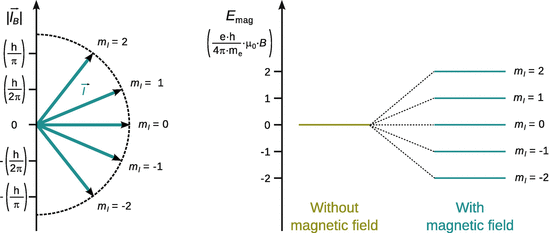
Fig. 10.7

Space quantisation illustrated for an electron in the d orbital. Left: Possible directions of the orbital angular momentum with respect to an external magnetic field . Right: Space quantisation in the presence of an external magnetic field leads to a potential magnetic energy E _mag

10.2.2 The Spin Quantum Number

Based on the considerations in the previous section, one would expect that the spectral lines of atomic hydrogen split into three (l = 1) or five (l = 2) lines in the presence of an external magnetic field. However, experimentally it is observed that the spectral lines split into even numbered sets when a magnetic field is present. The pivotal discovery by George Uhlenbeck and Samuel Goudsmit in 1925 was the fact that electrons not only orbit the atomic nucleus but also rotate around their own axis, leading to the term electron spin. In addition to the orbital angular momentum , one thus also needs to consider a spin momentum , which is characterised by a spin quantum number s. In contrast to all other quantum numbers, the spin quantum number only assumes one value:

(10.16)

In analogy to the magnetic quantum number m _l (Eq. 9.27), it follows for the magnetic spin quantum number m _s :

(10.17)

and therefore assumes the values of −1/2 or 1/2.

The general considerations we introduced for the orbital angular momentum (Eqs. 10.14 and 10.15) are also valid for the spin momentum and thus lead to the equations:

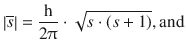
(10.18)

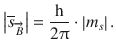
(10.19)

With s only assuming one value (s = 1/2), this means that the spin momentum for all electrons is the same, regardless of the orbital they occupy:

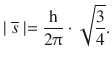
(10.20)

Also, there are only two possible states with respect to an external magnetic field (Fig. 10.8).

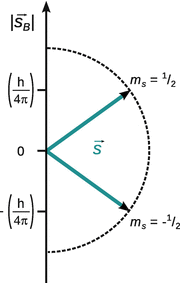
Fig. 10.8

Possible directions of the electron spin with respect to an external magnetic field

10.2.3 Spin—Orbit Coupling

We mentioned earlier (Sect. 10.2.1) that orbiting of an electron around the atomic nucleus gives rise to a magnetic field. If an electron spins around its own axis, as we have just introduced in the preceding section, then this also constitutes the motion of a charge which also induces a magnetic field. Both of those magnetic fields couple and result in a total angular momentum

(10.21)

which is characterised by the quantum number j of the total angular momentum. The values assumed by j combine the angular quantum number l and the spin quantum number s:

(10.22)

For example, for an electron in a p orbital where l = 1 and s = 1/2, this yields:

The magnetic quantum number of the total angular momentum, m _j , can generally assume the values:

(10.23)

and specifically for the above example of the electron in the p orbital:

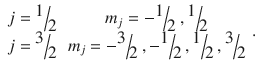
This shows that through the spin−orbit coupling, there are already two energetically different states in the p orbital: one with j = 1/2, and one with j = 3/2. If an external magnetic field is applied, these states split up further, characterised by the magnetic quantum number of the total angular momentum (Fig. 10.9). The external magnetic field causes the disappearance of the degeneracy in the two j-states, resulting in two energy levels for j = 1/2 and four energy levels for j = 3/2, in agreement with the observed splitting of lines in the atomic spectra.

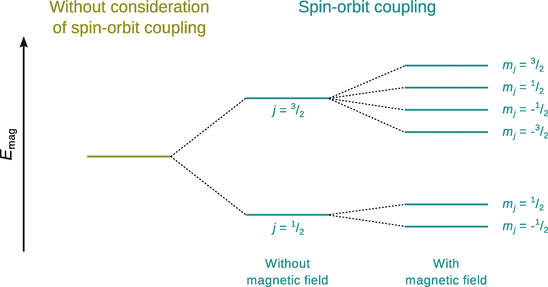
Fig. 10.9

Spin—orbit coupling of an electron in the p orbital. Even in the absence of an external magnetic field, there are two different states of the total angular momentum. In the presence of an external magnetic field, these two states split into further states (Zeeman effect)