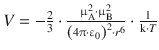Physico-chemical Data and Resources
1.4 Summary of Important Formulae and Equations

Thermodynamics

Boyle’s law

The pressure exerted by an ideal gas is inversely proportional to the volume it occupies if the temperature and amount of gas remain unchanged within a closed system.

V ∼ T

Charles’ law

Gases tend to expand when heated; at constant pressure, the volume is directly proportional to the temperature.

p ∼ T

Gay-Lussac’s law

If mass and volume of a gas are held constant, the pressure exerted by the gas increases directly proportional to the temperature.

p ⋅ V = n ⋅ R ⋅ T

Ideal gas equation

The laws by Boyle, Charles and Gay-Lussac combine to the ideal gas equation.

p _solute = K _solute ⋅ x _solute

Henry’s law

For solutions at low concentrations, the vapour pressure of the solute is proportional to its mole fraction.

Heat capacity at constant volume.

Variation of the internal energy of an ideal gas with volume at constant pressure.

Heat capacity at constant pressure.

Ideal gas:

Otherwise:

Change of enthalpy of a system with respect to a pressure change in an isothermal process. For an ideal gas, there is no change in enthalpy with pressure if the temperature remains the same.

C _p − C _V = n ⋅ R

Relationship between heat capacities of an ideal gas.

Maxwell relations provide a means to exchange thermodynamic functions.

Entropy change of a system with respect to temperature change in an isobaric process.

The pressure dependence of the Gibbs free energy of an isothermal process defines the volume change of the system during that process.

The temperature dependence of the Gibbs free energy of an isobaric process defines the entropy change during that process.

Clapeyron equation

Change of vapour pressure of a one-component system with temperature in terms of entropy.

Clausius-Clapeyron equation

Change of vapour pressure of a one-component system with temperature in terms of enthalpy.

van’t Hoff equations: reaction isobar and isochore

Change of the equilibrium constant of a chemical reaction with temperature. The two equations show the case for isothermal and isobaric, or isothermal and isochoric reactions.

van Laar-Planck isotherm

Change of the equilibrium constant of a chemical equilibrium with pressure in terms of the standard reaction volume.

ΔG = ΔG ^— + R ⋅ T ⋅ ln K

Change of the Gibbs free energy of a chemical reaction with equilibrium constant K and standard Gibbs free energy ΔG ^—.

Colligative properties

Π = i ⋅ c ⋅ R ⋅ T

Osmotic pressure

ΔT _f = i ⋅ K _f ⋅ b

Freezing point depression

ΔT _b = i ⋅ K _b ⋅ b

Boiling point elevation

p = p ^∗ ⋅ x

Raoult’s law: vapour pressure depression

Electrochemistry

Electrical conductance

The conductance increases with the cross-sectional area A and decreases with the length l of the conductor; k is the electrical conductivity. The conductance is the inverse of the resistance R.

Molar conductivity

m ∼ I ⋅ t = Q

Faraday’s first law of electrolysis

The mass of a substance altered at an electrode during electrolysis is directly proportional to the quantity of electricity transferred at that electrode.

Faraday’s second law of electrolysis

For a given quantity of electric charge, the mass of a deposited/generated elementary substance is proportional to the molar mass of that substance divided by the change in oxidation state (i.e. in most cases the charge of the cation in the electrolyte).

Nernst equation

Concentration dependence of the Redox potential.

Change of the standard molar Gibbs free energy of an electrochemical process with the standard electrode potential E ^— and the charge state z.

Henderson-Hasselbalch equation

pH of a solution with the buffer system consisting of the weak acid HA and its conjugated base A⁻.

Kohlrausch’s law

The molar conductivity of strong electrolytes increases with decreasing concentrations (valid for generally low concentrations).

Ostwald’s law of dilution

The dissociation constant of weak electrolytes is a function of the degree of dissociation α, and with , can be expressed in terms of the molar conductivity.

Λ_0m = ν₊ ⋅ λ ₊ + ν_‐ ⋅ λ _‐

Law of the independent migration of ions

The limiting molar conductivity is comprised of the two independent limiting molar conductivities of the anions and cations.

Transport

Thermodynamic force

A concentration gradient establishes a thermodynamic force F.

Fick’s first law of diffusion

Flux of matter is defined by the concentration gradient along x; is the molecule density; D is the diffusion coefficient.

Thermal conduction

Flux of energy along a temperature gradient; κ is the thermal conductivity.

Flux of momentum

When molecules switch from one flow layer to another, their momentum is also migrating; η is the viscosity.

Kinetics

Arrhenius equation

The rate constants of most reactions depend on the temperature.

The generalised dependency of rate constants on temperature, which applies to all reactions irrespective of their adhering to the Arrhenius relation or not.

Michaelis-Menten enzyme kinetics

Surface adsorption

Langmuir adsorption isotherm without dissociation

The Langmuir constant K is the ratio of the rate constants for adsorption and desorption: .

Langmuir adsorption isotherm with dissociation into two species

Order

Differential form

Integrated form

Half life

0

c(A) = − ν_A ⋅ k ⋅ t + c ₀(A)

1

− ln c(A) = ν_A ⋅ k ⋅ t − ln c ₀(A)

2

3

Interaction

Potential energy

Explanation

Order of magnitude (kJ mol⁻¹)

Covalent bond

|V| = 200—800

Coulomb interaction

Interaction between two ions

|V| = 40—400

Ion-dipole interaction

Interaction between ion and permanent dipole

|V| = 4—40

Keesom interaction

Interaction between two permanent dipoles

|V| = 0.4—4

Ion-induced dipole interaction

Interaction between ion and induced dipole

|V| = 0.4—4

Debye force

Interaction between permanent dipole and induced dipole

|V| = 0.4—4

London dispersion force

(pure substance)

Interaction between temporary dipole and induced dipole

|V| < 0.4

(mixture of A and B)

|V| < 0.4

Hydrogen bond

|V| = 4—40

Model/Transition

Energy

Selection criteria

Nuclear magnetic resonance

, with m _I = − I, − I + 1, …, I − 1, I

Electron spin resonance

, with

Δm _s = ±1; Δm _I = 0

Rigid rotor with space-free axis

E(J) = h ⋅ c ⋅ B ⋅ J ⋅ (J + 1)

ΔJ = ±1

Harmonic oscillator

Δv = ±1

Anharmonic oscillator

Δv = ±1, ±2, ±3, …

Rota-vibrational absorption (Infrared spectroscopy)

E = E(J) + E(v)

Δv = ±1 (±2, ±3, …); ΔJ = ±1

Singlet molecules

Δv = ±1 (±2, ±3, …); ΔJ = 0, ±1

Non-singlet molecules

Rota-vibrational emission (Raman spectroscopy)

E = E(J) + E(v)

Δv = ±1; ΔJ = 0, ±2

Electronic absorption (UV/Vis spectroscopy)

E = E(J) + E(v) + E _electr

M = 2 ⋅ S + 1 = const. ⇔ ΔS = 0

Electronic emission (Fluorescence)

E = E(J) + E(v) + E _electr

M = const. ⇔ ΔS = 0

Electronic emission (Phosphorescence)

E = E(J) + E(v) + E _electr

M ≠ const. ⇔ ΔS ≠ 0

Optical spectra of atoms

E = E _electr

Δl = ±1, Δj = 0, ±1

Alkali metals

ΔJ = 0, ±1

Multi-electron atoms

Nuclear resonance

E ² < 2 ⋅ m ⋅ c² ⋅ k_B ⋅ Θ

X-ray spectra of atoms

E = E _electr

Δl = ±1, Δj = 0, ±1

Auger electron spectra

none