Physical Chemistry Essentials - Hofmann A. 2018
The Chemical Bond
11.1 The Ionic Bond
After considering the make-up of isolated atoms, we now want to have a closer look at how atoms interact with each other to form compounds and molecules. Practical experiences with different substances tell us that the type of bonds between atoms can be quite different.
When combining two atoms of substantially different ionisation energies, such as for example observed with alkali halides (see Fig. 10.12), one can expect a tendency of an electron being transferred from one atom to another, resulting in the generation of ions. These substances are thus likely to form bonds based on electrostatic interactions, i.e. ionic bonds. A different type of bond is to be expected between atoms that have similar or the same ionisation energies, such as e.g. gaseous hydrogen or diamond. These types of substances are formed by covalent bonds. Yet a different type of substance are metals. While also being formed by interactions of atoms of the same element, the main difference of metals when compared to covalently bonded substances is the fact that they can conduct electric current. The metallic bond therefore must have particular features. Last, we know that noble gases generally resist chemical reactions and, for large parts, do not engage in compound formation. However, even noble gases form liquid and solid phases. In those states, the noble gas atoms are held together by van der Waals interactions.
In the following sections, we will discuss these four types of chemical bonds, but appreciate that these are particularly distinct instances; there will also be many cases where the type of chemical bond is a mixture of two of these distinct bonding types.
11.1 The Ionic Bond
As an example for an ionic substance we will consider the alkali halide NaCl which adopts a cubic close-packed crystal structure where every individual ion is surrounded by six counter-ions sitting on the vertices of an octahedron (Fig. 11.1).
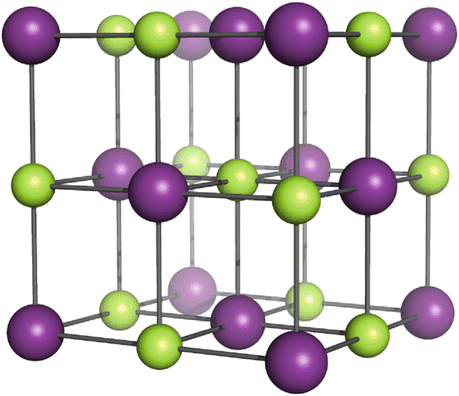
Fig. 11.1
Cubic close packing of NaCl. Na+ ions are shown in green, Cl− ions in magenta. Sphere sizes have been decreased to allow drawing of the crystal lattice
The force describing the electrostatic interaction between two ions of charge Q 1 and Q 2 is given by Coulomb’s law:
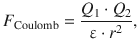
(11.1)
where ε is the dielectric constant of the medium. Since energy is the product of force and distance:
![]()
(11.2)
the potential energy between two ions is due to the Coulomb force of electrostatic attraction and given by
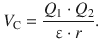
(11.3)
For two ions with the charge numbers z + and z − in a crystal ε lattice, this yields the following expression:
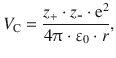
(11.4)
where we replaced the dielectric constant ε with the vacuum permittivity ε0 (more precisely the product 4π·ε0) introduced in Sect. 8.2.2. Note that the numerical value of the Coulomb potential energy V C in Eq. 11.4 is negative, since z + has a positive and z − a negative sign. V C thus assumes an indefinite negative value at r = 0, i.e. when both ions collapse. This is certainly not what we observe. The Coulomb potential energy thus describes the real phenomenon only when the two ions are at sufficient distance from each other.
As two particles get spatially very close, the short-range repulsion forces gain weight. Therefore, we also need to consider a potential energy V R describing this repulsion which may be modelled in this case by
![]()
(11.5)
where A and ρ are constants.
The total potential energy between two ions in the lattice is thus a composite of the attractive (Coulomb) and the repulsive terms:
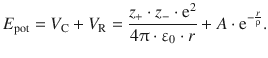
(11.6)
As illustrated in Fig. 11.2, the total potential energy E pot possesses a minimum at a particular distance r eq which is the equilibrium distance between the two ions.
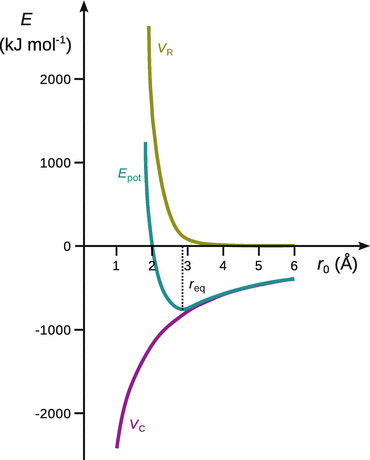
Fig. 11.2
Potential energy of the ionic bond, illustrated for NaCl
Since there are more than two ions in an ionic crystal, we need to consider all possible inter-ionic interactions. Therefore, we first focus on one cation which has a charge z + and the distance of this ion to each other ion with running index i shall be r +,i. We thus obtain for the Coulomb potential energy for this cation:
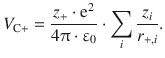
Similarly, this approach yields for the Coulomb potential energy of a particular anion:
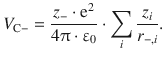
Since the distances do not vary continuously, but systematically due to the regular arrangement of ions in the lattice, r +,i and r −,i can be expressed as multiples of a smallest distance r 0:
![]()
Further, we need to make sure that the interactions between cat- and anions are not counted twice when combining V C+ and V C−, and thus introduce a factor of 1/2. Considering 1 mol of substance, we obtain for the molar Coulomb potential energy in the ionic crystal:
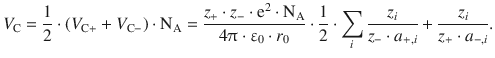
(11.7)
The factor
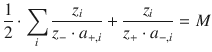
(11.8)
is called the Madelung constant M, named after the German physicist Erwin Madelung. This yields for the attractive (Coulomb) potential energy (Eq. 11.7) in the ionic crystal
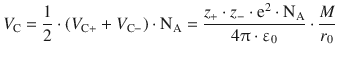
where z +, z − and r 0 are characteristic constants of a substance, and the Madelung constant M is a characteristic parameter capturing the geometric arrangements in a particular lattice type. Using the above expression, the total potential energy (Eq. 11.6) becomes
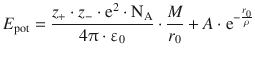
(11.9)
The lattice energy ΔU lattice of a crystal describes the energy required to break the bonds of 1 mol of an ionic solid under standard conditions; it equals the potential energy at the equilibrium distance r eq, i.e. the minimum of the function E pot(r 0 ) illustrated in Fig. 11.2. At the minimum of a function f(x), the derivative ![]() equals zero.
equals zero.
For the potential energy function in Eq. 11.9 this results in
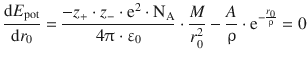
and allows calculation of the parameter A:
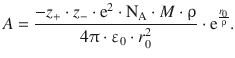
If we substitute this expression for A in Eq. 11.9 we obtain the following expression for the lattice energy of an ionic crystal:
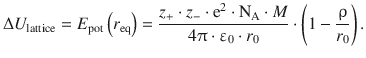
(11.10)
As mentioned above, the charge numbers z + and z − are characteristic parameters of a substance, r 0 is available from the lattice parameters for this substance and M is a geometric constant for a particular lattice type. The extent of the repulsion potential is expressed by ρ. We appreciate that this parameter is directly linked to the compressibility of the ionic crystal: the longer the range of the repulsion potential, the larger is ρ and the less the lattice can be compressed. The experimental determination of compressibility of solids thus allows determination of the parameter ρ.