Physical Chemistry Essentials - Hofmann A. 2018
The Chemical Bond
11.5 The van der Waals Bond
In the previous sections, we have seen that condensed matter can arise from different types of bonds, namely ionic (e.g. NaCl), metallic (e.g. Fe) and covalent (e.g. diamond). But what about the condensed phases such as for example the liquid or solid states of the noble gases, where the electronic configuration does not allow for covalent or ionic bonds?
The electrostatic potential of the nucleus is fully balanced by the electrons surrounding it. In the case of the noble gases, the electrons are distributed around the nucleus with spherical symmetry, due to full occupancy of all shells. However, this scenario describes the situation only in an averaged time window. Since the electrons are orbiting the nucleus, at any particular time, there may be a distribution that is not of spherical symmetry, and therefore leads to a temporary dipole momentum (see also Sect. 12.2). This dipole moment establishes an electric field whose value is given by
![]()
(11.17)
where μ1 is the dipole moment in atom A, r is the distance from the dipole and ε0 is the permittivity in vacuo. The electric field E then leads to an induced dipole moment in a neighbouring atom (atom B):
![]()
(11.18)
α is called the polarisability and discussed in more detail in Sect. 12.2.1.
The potential energy of a dipole in an electric field is given by the product between the two quantities and given a negative sign since it is an attractive interaction:
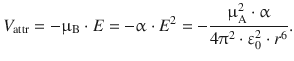
(11.19)
The important relationship in above equation is that the attractive interaction between the two atoms (= temporary dipoles) varies with r −6:
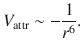
(11.20)
This attractive potential is called the van der Waals potential (see Fig. 11.8).
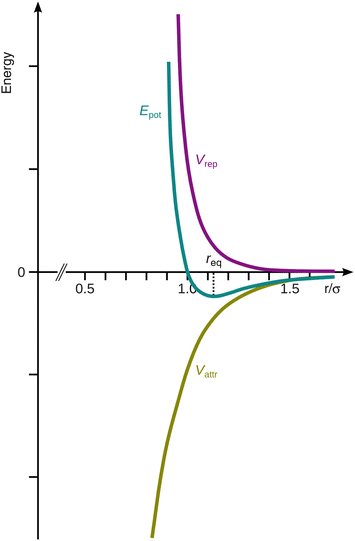
Fig. 11.8
The Lennard-Jones potential (E pot) as a combination of the attractive van der Waals potential (V attr) and the repulsive potential (V rep) between two atoms. The minimum in the potential curve occurs at the equilibrium distance r eq. ![]()
If the distance between two atoms is made less and less, the two atoms approach each other and their electron shells start to overlap. This universal repulsive force becomes stronger, the closer the two atoms get. Empirically, it was found that this potential varies with r −12 and is known as the Pauli repulsive potential:
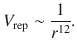
(11.21)
The sum of the above attractive and repulsive terms yields the potential between two particles based on temporary dipoles. The combination of the van der Waals and Pauli terms is called the Lennard-Jones potential:
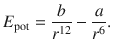
(11.22)
The universal repulsive force arises from two quantum mechanical principles and prevents two atoms from occupying the same space. It is indeed of universal importance since it gives rise compressibility and hardness of solids, was famously linked by Victor Weisskopf to the heights of mountains, lengths of ocean waves, and even sizes of stars (Weisskopf 1975). On the one hand, due to the uncertainty relationship by Heisenberg (see Sect. 8.1.6), the position of the electrons surrounding an atomic nucleus cannot be exactly located. They possess kinetic energy which results in a pressure that would drive them off the nucleus if they were not held back by the attractive force of the positively charged nucleus. If the volume occupied by the electrons was decreased by an approaching atom intruding in that space, the electron pressure would increase dramatically and thus resist this change in volume. Ultimately, this is also the reason why condensed matter can hardly be compressed.
On the other hand, according to the Pauli exclusion principle (see Sect. 10.3.2), the electrons in an atom must all have different quantum numbers. In the event of an approaching atom intruding into the space of another atom, some electrons are forced into higher quantum states to fulfil the exclusion principle. However, higher quantum states occupy larger volumes, thereby counteracting the attempted volume decrease by intruding atoms.