Physical Chemistry Essentials - Hofmann A. 2018

The Chemical Bond
11.6 Crystal Field and Ligand Field Theory

As we have seen earlier, a further level of complexity arises in transition metals since they populate the fivefold degenerate d orbitals. We found that four of the d orbitals possess a very similar shape and differ mainly in the orientation of the different lobes (see Fig. 11.9). The fifth d orbital was unique as it extends its two lobes along the z-axis and has a torus around its equator.

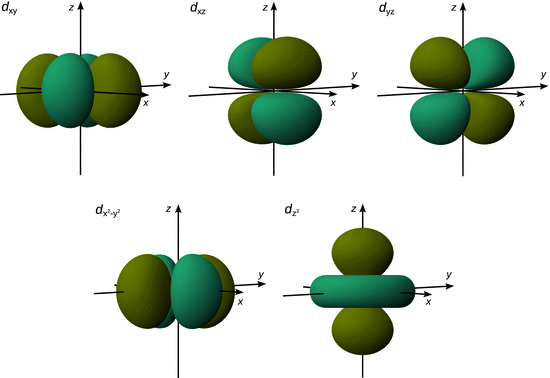
Fig. 11.9

Three-dimensional graphs of the five d orbitals of the third shell (principal quantum number n = 3) with respect to a Cartesian coordinate system

In an isolated transition metal atom, the five d orbitals are fully degenerate and possess the same energy. However, when the transition metal engages in a complex where it interacts with ligands that are distribution around it in a particular spatial distribution, ligands perturb the d orbitals that extend into their direction, thereby affecting the energies of the individual d orbitals. Those d orbitals that do not extend into the direction of a ligand are stabilised (their energy decreases) and the other d orbitals whose lobes extend into the direction of the ligands are destabilised (their energies increase). This concept is known as the crystal field theory and the energy difference between the stabilised and destabilised d orbitals is called the crystal field splitting Δ.

11.6.1 Crystal Field Splitting

Obviously, the way in which the degenerate d orbitals split upon complex formation depends on the geometry of the complex. The geometries of transition metal complexes mainly consist of tetrahedral, octahedral and square planar arrangements; the crystal field splitting for these cases is illustrated in Fig. 11.10.

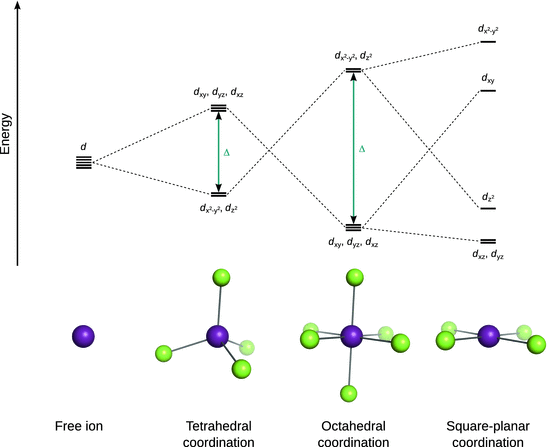
Fig. 11.10

Energetic splitting of d orbitals in response to different coordination geometries. Those orbitals that extend along a direction projects towards a ligand are destabilised and move to higher energy; the others are stabilised and move to lower energy

Importantly, the magnitude of Δ, which can be measured spectroscopically (d-d-transitions), depends on the identity and charge of the metal ion, as well as the type of ligand. By characterising a range of different ligands, a spectrochemical series can be established which lists the ligands in the order of increasing Δ:

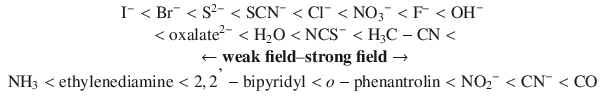
Given the same geometry of coordination and identical ligands, the crystal field splitting Δ for different metals increases in the following order:

Because a complex with tetrahedral geometry has fewer ligands than a complex with octahedral geometry, the magnitude of the crystal field splitting observed with tetrahedral coordination (Δ_t) is smaller than with octahedral coordination (Δ_o):

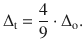
(11.23)

11.6.2 Low-Spin and High-Spin Complexes

The magnitude of the crystal field splitting Δ can affect the electronic configuration, and thus the magnetic properties of a complex; in particular, if there are several electrons populating the d orbitals, such as for example in Fe³⁺.

As illustrated in Fig. 11.11, electrons are filled into the orbitals according to the principles we have established before. One electron is added to each of the degenerate orbitals until each orbital has one electron with the same spin. In an octahedral complex, this works straightforward up to the third electron. The fourth electron could either be placed as a paired electron in the lower set of d orbitals ( low-spin complex) or as an unpaired electron in the energetically higher set of d orbitals ( high-spin complex). Whether the first or the second scenario happens depends on the magnitude of crystal field splitting Δ. Therefore, high-spin complexes are typically found with metals/ligands at the weak-field end of the spectrochemical series (such as e.g. [FeCl₆]³⁻); vice versa, low-spin complexes are expected in complexes that comprise of metals and ligands at the high-field end of the spectrochemical series (such as e.g. [Fe(CN)₆]³⁻). Since the formation of either a high-spin or a low-spin complex affects the pairing of electrons, the crystal field splitting has repercussions in the magnetic properties of a complex.

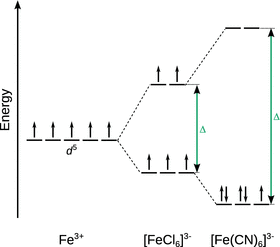
Fig. 11.11

Comparison of crystal field splitting for two Fe³⁺ complexes

Importantly, with octahedral geometry, the options of forming either low-spin or high-spin complexes only exist for systems with 4—7 electrons in the d orbitals (d ⁴, d ⁵, d ⁶, d ⁷ complexes). For d ¹, d ² d ³ and d ⁸, d ⁹, d ¹⁰ complexes, there is only one possible electron configuration.

11.6.3 Ligand Field Theory

Properties such as the absorption of visual light due to d-d-transitions and magnetic susceptibility of metal complexes can be macroscopically observed, and the crystal field theory delivers predictions that are in good agreement with macroscopic observations for some complexes. However, the concept has a fundamental shortcoming in that it only considers the electrostatic interactions between metal and ligands, and ignores any covalent character of metal-ligand bonds; you may have noticed that the ligand orbitals are not actually featured in Fig. 11.11.

The ligand field theory overcomes this defect by also taking into account covalent contributions of metal-ligand interactions. To apply this concept, we construct molecular orbitals as introduced earlier (Sect. 11.3.2). The d orbitals that do not extend into the direction of the coordinated ligands are now deemed to not take part in bond formation and thus called non-bonding orbitals. Accordingly, their energy does not change as compared to the set of degenerate d orbitals in the free metal ion.

This concept is illustrated for [FeCl₆]³⁻ in Fig. 11.12. The Fe³⁺ ion possesses five electrons in the 3d orbitals and has empty 4s and 4p orbitals. Energetically, the 3d, 4s and 4p orbitals are at a level that allows molecular orbital formation with the atomic orbitals provided by the six chloride ligands. In this scheme, a total of 17 electrons need to be filled, twelve of which occupy the bonding orbitals. The three non-bonding d orbitals (coloured red in Fig. 11.12) and the two anti-bonding orbitals (upper pair of yellow coloured orbitals in Fig. 11.12) arising from the linear combination of two 3d orbitals with the two ligand orbitals results in an energetic scheme we have already seen in the discussion of the crystal field theory. Therefore, the crystal field splitting Δ is also observed in the ligand field theory.

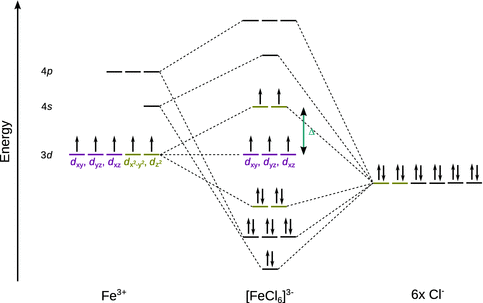
Fig. 11.12

Molecular orbitals for [FeCl₆]³⁻