1,001 Calculus Practice Problems
Part I
The Questions
Chapter 14
Trigonometric Integrals, Trigonometric Substitution, and Partial Fractions
This chapter covers trigonometric integrals, trigonometric substitutions, and partial fractions — the remaining integration techniques you encounter in a second-semester calculus course (in addition to u-substitution and integration by parts; see Chapter 13). In a sense, these techniques are nothing fancy. For the trigonometric integrals, you typically use a u-substitution followed by a trigonometric identity, possibly throwing in a bit of algebra to solve the problem. For the trigonometric substitutions, you're often integrating a function involving a radical; by picking a clever substitution, you can often remove the radical and make the problem into a trigonometric integral and proceed from there. Last, the partial fractions technique simply decomposes a rational function into a bunch of simple fractions that are easier to integrate.
With that said, many of these problems have many steps and require you to know identities, polynomial long division, derivative formulas, and more. Many of these problems test your algebra and trigonometry skills as much as your calculus skills.
The Problems You'll Work On
This chapter finishes off the integration techniques that you see in a calculus class:
· Solving definite and indefinite integrals involving powers of trigonometric functions
· Solving definite and indefinite integrals using trigonometric substitutions
· Solving definite and indefinite integrals using partial fraction decompositions
What to Watch Out For
You can get tripped up in a lot of little places on these problems, but hopefully these tips will help:
· Not all of the trigonometric integrals fit into a nice mold. Try identities, u-substitutions, and simplifying the integral if you get stuck.
· You may have to use trigonometry and right triangles in the trigonometric substitution problems to recover the original variable.
· If you've forgotten how to do polynomial long division, you can find some examples in Chapter 1's algebra review.
· The trigonometric substitution problems turn into trigonometric integral problems, so make sure you can solve a variety of the latter problems!
Trigonometric Integrals
884–913 Find the antiderivative or evaluate the definite integral.
884. ![]()
885. ![]()
886. ![]()
887. ![]()
888. ![]()
889. ![]()
890. ![]()
891. ![]()
892. ![]()
893. ![]()
894. ![]()
895. ![]()
896. ![]()
897. ![]()
898. ![]()
899. ![]()
900. ![]()
901. 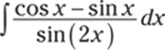
902. ![]()
903. ![]()
904. ![]()
905. ![]()
906. ![]()
907. ![]()
908. ![]()
909. ![]()
910. ![]()
911. ![]()
912. ![]()
913. ![]()
Trigonometric Substitutions
914–939 Evaluate the integral using a trigonometric substitution.
914. 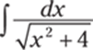
915. 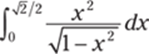
916. ![]()
917. 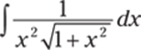
918. 
919. ![]()
920. ![]()
921. 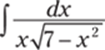
922. ![]()
923. 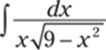
924. 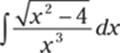
925. ![]()
926. 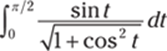
927. 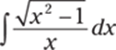
928. 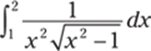
929. 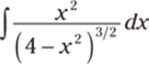
930. 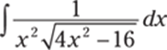
931. 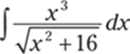
932. 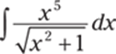
933. ![]()
934. ![]()
935. 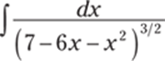
936. ![]()
937. ![]()
938. ![]()
939. ![]()
Finding Partial Fraction Decompositions (without Coefficients)
940–944 Find the partial fraction decomposition without finding the coefficients.
940. 
941. ![]()
942. 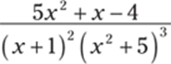
943. 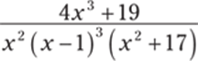
944. 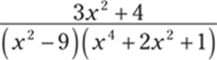
Finding Partial Fraction Decompositions (Including Coefficients)
945–949 Find the partial fraction decomposition, including the coefficients.
945. 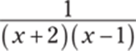
946. ![]()
947. ![]()
948. ![]()
949. 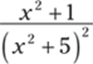
Integrals Involving Partial Fractions
950–958 Evaluate the integral using partial fractions.
950. ![]()
951. ![]()
952. 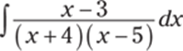
953. ![]()
954. ![]()
955. ![]()
956. ![]()
957. ![]()
958. ![]()
Rationalizing Substitutions
959–963 Use a rationalizing substitution and partial fractions to evaluate the integral.
959. ![]()
960. ![]()
961. ![]()
962. ![]()
963. ![]()