1,001 Calculus Practice Problems
Part I
The Questions
Chapter 5
The Product, Quotient, and Chain Rules
This chapter focuses on some of the major techniques needed to find the derivative: the product rule, the quotient rule, and the chain rule. By using these rules along with the power rule and some basic formulas (see Chapter 4), you can find the derivatives of most of the single-variable functions you encounter in calculus. However, after using the derivative rules, you often need many algebra steps to simplify the function so that it's in a nice final form, especially on problems involving the product rule or quotient rule.
The Problems You'll Work On
Here you practice using most of the techniques needed to find derivatives (besides the power rule):
· The product rule
· The quotient rule
· The chain rule
· Derivatives involving trigonometric functions
What to Watch Out For
Many of these problems require one calculus step and then many steps of algebraic simplification to get to the final answer. Remember the following tips as you work through the problems:
· Considering simplifying a function before taking the derivative. Simplifying before taking the derivative is almost always easier than finding the derivative and then simplifying.
· Some problems have functions without specified formulas in the questions; don't be thrown off! Simply proceed as you normally would on a similar example.
· Many people make the mistake of using the product rule when they should be using the chain rule. Stop and examine the function before jumping in and taking the derivative. Make sure you recognize whether the question involves a product or a composition (in which case you must use the chain rule).
· Rewriting the function by adding parentheses or brackets may be helpful, especially on problems that involve using the chain rule multiple times.
Using the Product Rule to Find Derivatives
312–331 Use the product rule to find the derivative of the given function.
312. f (x) = (2x3 + 1)(x5 – x)
313. f (x) = x2 sin x
314. f (x) = sec x tan x
315. ![]()
316. f (x) = 4x csc x
317. Find (fg)'(4) if f (4) = 3, f '(4) = 2, g(4) = –6, and g '(4) = 8.
318. ![]()
319. f (x) = (sec x)(x + tan x)
320. ![]()
321. f (x) = 4x3 sec x
322. ![]()
323. Assuming that g is a differentiable function, find an expression for the derivative of f (x) = x2g(x).
324. Assuming that g is a differentiable function, find an expression for the derivative of ![]() .
.
325. Find (fg)'(3) if f (3) = –2, f '(3) = 4, g(3) = –8, and g '(3) = 7.
326. f (x) = x2 cos x sin x
327. Assuming that g is a differentiable function, find an expression for the derivative of 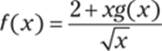 .
.
328. 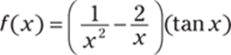
329. 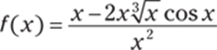
330. Assuming that g is a differentiable function, find an expression for the derivative of ![]() .
.
331. Assuming that g and h are differentiable functions, find an expression for the derivative of ![]() .
.
Using the Quotient Rule to Find Derivatives
332–351 Use the quotient rule to find the derivative.
332. ![]()
333. ![]()
334. ![]()
335. ![]()
336. Assuming that f and g are differentiable functions, find the value of 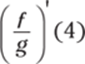 if f (4) = 5, f '(4) = –7, g(4) = 8, and g'(4) = 4.
if f (4) = 5, f '(4) = –7, g(4) = 8, and g'(4) = 4.
337. ![]()
338. ![]()
339. ![]()
340. ![]()
341. ![]()
342. ![]()
343. Assuming that f and g are differentiable functions, find the value of 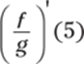 if f (5) = –4, f '(5) = 2, g(5) = –7, and g'(5) = –6.
if f (5) = –4, f '(5) = 2, g(5) = –7, and g'(5) = –6.
344. 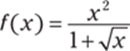
345. ![]()
346. 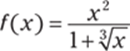
347. 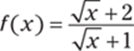
348. ![]()
349. 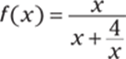
350. Assuming that g is a differentiable function, find an expression for the derivative of ![]() .
.
351. Assuming that g is a differentiable function, find an expression for the derivative of ![]() .
.
Using the Chain Rule to Find Derivatives
352–370 Use the chain rule to find the derivative.
352. ![]()
353. f (x) = sin(4x)
354. ![]()
355. 
356. 
357. ![]()
358. ![]()
359. f (x) = cos(x sin x)
360. ![]()
361. ![]()
362. f (x) = sec2 x + tan2 x
363. ![]()
364. ![]()
365. ![]()
366. 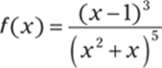
367. ![]() , where x > 1
, where x > 1
368. ![]()
369. ![]()
370. ![]()
More Challenging Chain Rule Problems
371–376 Solve the problem related to the chain rule.
371. Find all x values in the interval [0, 2π] where the function f (x) = 2 cos x + sin2 x has a horizontal tangent line.
372. Suppose that H is a function such that ![]() for x > 0. Find an expression for the derivative of
for x > 0. Find an expression for the derivative of ![]() .
.
373. Let ![]() , g(2) = –2, g'(2) = 4, f'(2) = 5, and f'(–2) = 7. Find the value of F'(2).
, g(2) = –2, g'(2) = 4, f'(2) = 5, and f'(–2) = 7. Find the value of F'(2).
374. Let ![]() , f (2) = –2, f'(2) = –5, and f'(–2) = 8. Find the value of F'(2).
, f (2) = –2, f'(2) = –5, and f'(–2) = 8. Find the value of F'(2).
375. Suppose that H is a function such that ![]() for x > 0. Find an expression for the derivative of f (x) = H(x3).
for x > 0. Find an expression for the derivative of f (x) = H(x3).
376. Let ![]() , g(4) = 6, g'(4) = 8, f '(4) = 2, and f '(6) = 10. Find the value of F '(4).
, g(4) = 6, g'(4) = 8, f '(4) = 2, and f '(6) = 10. Find the value of F '(4).