A Book of Abstract Algebra, Second Edition (1982)
Chapter 10. ORDER OF GROUP ELEMENTS
Let G be an arbitrary group, with its operation denoted multiplicadvely. Exponential notation is a convenient shorthand: for any positive integer n, we will agree to let
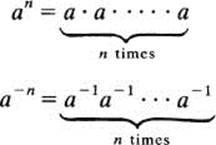
and
a0 = e
Take care to observe that we are considering only integer exponents, not rational or real exponents. Raising a to a positive power means multiplying a by itself the given number of times. Raising a to a negative power means multiplying a−1 by itself the given number of times. Raising a to the power 0 yields the group’s identity element.
These are the same conventions used in elementary algebra, and they lead to the same familiar “laws of exponents.”
Theorem 1: Laws of exponents if G is a group and a ∈G, the following identities hold for all integers m and n:
(i) aman = am+n
(ii) (am)n = amn
(iii) a−n = (a−l)n = (an)−l
These laws are very easy to prove when m and n are positive integers. Indeed,
(i) ![]()
(ii) ![]()
Next, by definition a−n = a−1 ··· a−1 = (a−1)n. Finally, since the inverse of a product is the product of the inverses in reverse order,
(an)−1 = (aa ··· a)−1 = a−1a−1 ··· a−1 = a−n
To prove Theorem 1 completely, we need to check the other cases, where each of the integers m and n is allowed to be zero or negative. This routine case-by-case verification is left to the student as Exercise A at the end of this chapter.
In order to delve more deeply into the behavior of exponents we must use an elementary but very important property of the integers: From elementary arithmetic we know that we can divide any integer by any positive integer to get an integer quotient and an integer remainder. The remainder is nonnegative and less than the dividend. For example, 25 may be divided by 8, giving a quotient of 3, and leaving a remainder of 1:
![]()
Similarly, −25 may be divided by 8, with a quotient of −4 and a remainder of 7:
![]()
This important principle is called the division algorithm. In its precise form, it may be stated as follows:
Theorem 2: Division algorithm if m and n are integers and n is positive, there exist unique integers q and r such that
m = nq + r and 0 ≥ r < n
We call q the quotient, and r the remainder, in the division of m by nx.
At this stage we will take the division algorithm to be a postulate of the system of the integers. Later, in Chapter 19, we will turn things around, starting with a simpler premise and proving the division algorithm from it.
Let G be a group, and a an element of G. Let us observe that
If there exists a nonzero integer m such that am = e, then there exists a positive integer n such that an = e.
Indeed, if am = e where m is negative, then a−m = (am)−1 = e−1 = e. Thus, a−m = e where −m is positive. This simple observation is crucial in our next definition. Let G be an arbitrary group, and a an element of G:
Definition If there exists a nonzero integer m such that am – e, then the order of the element a is defined to be the least positive integer n such that an = e.
If there does not exist any nonzero integer m such that am = e, we say that a has order infinity.
Thus, in any group G, every element has an order which is either a positive integer or infinity. If the order of a is a positive integer, we say that a has finite order; otherwise, a has infinite order. For example, let us glance at S3, whose table appears on page 72. (It is customary to use exponential notation for composition: for instance, β ∘ β = β2, β ∘ β ∘ β = β3, and so on.) The order of α is 2, because α2 = ε and 2 is the smallest positive integer which satisfies that equation. The order of β is 3, because β3 = ε, and 3 is the lowest positive power of β equal to ε. It is clear, similarly, that γ has order 2, δ has order 3, and κ has order 2. What is the order of ε?
It is important to note that one speaks of powers of a only when the group’s operation is called multiplication. When we use additive notation, we speak of multiples of a instead of powers of a. The positive multiples of a are a, a + a, a + a + a, and so on, while the negative multiples of a are −a,(−a) + (−a), (−a) + (−a) + (−a), and so on. In ![]() 6, the number 2 has order 3, because 2 + 2 + 2 = 0, and no smaller multiple of 2 is equal to 0. Similarly, the order of 3 is 2, the order of 4 is 3, and the order of 5 is 6.
6, the number 2 has order 3, because 2 + 2 + 2 = 0, and no smaller multiple of 2 is equal to 0. Similarly, the order of 3 is 2, the order of 4 is 3, and the order of 5 is 6.
In ![]() , the number 2 has infinite order, because no nonzero multiple of 2 is equal to 0. As a matter of fact, in
, the number 2 has infinite order, because no nonzero multiple of 2 is equal to 0. As a matter of fact, in ![]() , every nonzero number has infinite order.
, every nonzero number has infinite order.
The main fact about the order of elements is given in the next two theorems. In each of the following theorems, G is an arbitrary group and a is any element of G.
Theorem 3: Powers of a, if a has finite order if the order of a is n, there are exactly n different powers of a, namely,
a0, a, a2, a3, …, an−1
What this theorem asserts is that every positive or negative power of a is equal to one of the above, and the above are all different from one another.
Before going on, remember that the order of a in n, hence
an = e
and n is the smallest positive integer which satisfies this equation.
PROOF OF THEOREM 3: Let us begin by proving that every power of a is equal to one of the powers a0,a1,a2, …, an−1. Let am be any power of a. Use the division algorithm to divide m by n:
m = nq + r0 ≤ r < n
Then am = anq +r = (anqar = (an)qar = eqar = ar
Thus, am = ar, and r is one of the integers 0,1, 2, …, n − 1.
Next, we will prove that a0,a1,a2, …, an−1 are all different, Suppose not; suppose ar = as, where r and s are distinct integers between 0 and n − 1. Either r < s or s < r, say s < r. Thus 0 ≤ s < r < n, and consequently,
0 < r − s < n (1)
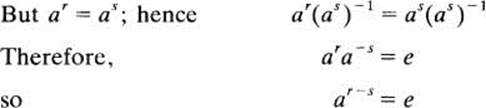
However, this is impossible, because by Equation (1), r − s is a positive integer less than n, whereas n (the order of a) is the smallest positive integer such that an = e.
This proves that we cannot have ar = as where r ≠ s. Thus, a0, a1, a2, …, an − 1 are all different! ■
Theorem 4: Powers of a, if a has infinite order If a has order infinity, then all the powers of a are different. That is, if r and s are distinct integers, then ar ≠ as.
PROOF: Let r and s be integers, and suppose ar = as.

But a has order infinity, and this means that am is not equal to e for any integer m expect 0. Thus, r − s = 0, so r = s. ■
This chapter concludes with a technical property of exponents, which is of tremendous importance in applications.
If a is an element of a group, the order of a is the least positive integer n such that an = e. But there are other integers, say t, such that a = e. How are they related to n? The answer is very simple:
Theorem 5 Suppose an element a in a group has order n. Then at = e iff t is a multiple of n (“t is a multiple of n” means that t = nq for some integer q).
PROOF: If t = nq, then at = anq = (an)q = eq = e. Conversely, suppose at = e. Divide t by n using the division algorithm:
t = nq + r0 ≤ r < n
Then
e = at = anq + r = (an)qar = eqar = ar
Thus, ar = e, where 0 ≤ r <n. If r ≠0, then r is a positive integer less than n, whereas n is the smallest positive integer such that an = e. Thus r = 0, and therefore t = nq. ■
If a is any element of a group, we will denote the order of a by
ord(a)
EXERCISES
A. Laws of Exponents
Let G be a group and a ∈ G.
# 1 Prove that aman = am + n in the following cases:
(a)m = 0
(b)m < 0 and n > 0
(c)m < 0 and n < 0
2Prove that (am)n = amn in the following cases:
(a)m = 0
(b)n = 0
(c)m < 0 and n > 0
(d)m > 0 and n < 0
(e)m < 0 and n < 0
3Prove that (an)− 1 = a− n in the following cases:
(a)n = 0
(b)n < 0
B. Examples of Orders of Elements
1What is the order of 10 in ![]() 25?
25?
2What is the order of 6 in ![]() 16?
16?
# 3What is the order of
![]()
in S6
4What is the order of 1 in ![]() *? What is the order of 1 in
*? What is the order of 1 in ![]() ?
?
5If A is the set of all the real numbers x ≠ 0,1,2, what is the order of
![]()
in SA?
6Can an element of an infinite group have finite order? Explain.
7In ![]() 24, list all the elements (a) of order 2; (b) of order 3; (c) of order 4; (d) of order 6.
24, list all the elements (a) of order 2; (b) of order 3; (c) of order 4; (d) of order 6.
C. Elementary Properties of Order
Let a, b, and c be elements of a group G. Prove the following:
1Ord(a) = 1iffa = e.
2If ord(a) = n, then an − r = (ar)−1.
3If ak = e where k is odd, then the order of a is odd.
# 4 Ord(a) = ord(bab −1).
5The order of a −l is the same as the order of a.
6The order of ab is the same as the order of ba. [HINT: if
![]()
then a is the inverse of x. Thus, ax = e.]
7Ord(abc) = ord(cab) = ord(bca).
8Let x = a1a2 ··· an, and let y be a product of the same factors, permuted cyclically. (That is, y = akak + 1 ··· ana1 ··· ak −1.) Then ord(x) = ord(y).
D. Further Properties of Order
Let a be any element of finite order of a group G. Prove the following:
1If ap = e where p is a prime number, then a has order p. (a ≠ e.)
# 2The order of ak is a divisor (factor) of the order of a.
3If ord(a) = km, then ord(ak) = m.
4If ord(a) = n where n is odd, then ord(a2) = n.
5 If a has order n, and ar = as, then n is a factor of r − s.
6If a is the only element of order k in G, then a is in the center of G. (HINT: Use Exercise C4. Also, see Chapter 4, Exercise C6.)
7If the order of a is not a multiple of ra, then the order of ak is not a multiple of m. (HINT: Use part 2.)
8If ord(a) = mk and ark = e, then r is a multiple of m.
† E. Relationship between ord (ab), ord (a), and ord (b)
Let a and b be elements of a group G. Let ord(a) = m and ord(b) = n; let lcm(m, n) denote the least common multiple of m and n. Prove parts 1–5:
1 If a and b commute, then ord(ab) is a divisor of lcm(m, n).
2 If m and n are relatively prime, then no power of a can be equal to any power of b (except for e). (REMARK: Two integers are said to be relatively prime if they have no common factors except ±1.) (HINT: Use Exercise D2.)
3 If m and n are relatively prime, then the products aibj (0 ≤ i < m, 0 ≤ j < n) are all distinct.
4 Let a and b commute. If m and n are relatively prime, then ord(ab) = mn. (HINT: Use part 2.)
5 Let a and b commute. There is an element c in G whose order is lcm(m, n). (HINT: Use part 4, above, together with Exercise D3. Let c = aib where ai is a certain power of a.)
6 Give an example to show that part 1 is not true if a and b do not commute.
Thus, there is no simple relationship between ord(ab), ord(a), and ord(b) if a and b fail to commute.
† F. Orders of Powers of Elements
Let a be an element of order 12 in a group G.
1 What is the smallest positive integer k such that a8k = e? (HINT: Use Theorem 5 and explain carefully!)
# 2 What is the order of a8?
3 What are the orders of a9, a10, a5?
4 Which powers of a have the same order as a? [That is, for what values of k is ord(ak) = 12?]
5 Let a be an element of order m in any group G. What is the order of ak? (Look at the preceding examples, and generalize. Do not prove.)
6 Let a be an element of order m in any group G. For what values of k is ord(ak) = m? (Look at the preceding examples. Do not prove.)
† G. Relationship between ord(a) and ord(ak)
From elementary arithmetic we know that every integer may be written uniquely as a product of prime numbers. Two integers m and n are said to be relatively prime if they have no prime factors in common. (For example, 15 and 8 are relatively prime.) Here is a useful fact: If m and n are relatively prime, and m is a factor of nk, then m is a factor of k. (Indeed, all the prime factors of m are factors of nk but not of n, hence are factors of k.)
Let a be an element of order n in a group G.
1 Prove that if m and n are relatively prime, then am has order n. (HINT: If amk = e, use Theorem 5 and explain why n must be a factor of k.)
2 Prove that if am has order n, then m and n are relatively prime. [HINT: Assume m and n have a common factor q >1, hence we can write m = m′ q and n = n′q. Explain why (am)n = e, and proceed from there.]
3 Let l be the least common multiple of m and n. Let l/m = k. Explain why (am)k = e.
4 Prove: If (am)t = e, then n is a factor of mt. (Thus, mt is a common multiple of m and n.) Conclude that
![]()
5 Use parts 3 and 4 to prove that the order of am is [lcm(m, n)]/m.
† H. Relationship between the Order of a and the Order of any kth Root of a
Let a denote an element of a group G.
1 Let a have order 12. Prove that if a has a cube root, say a = b3 for some b ∈ G, then b > has order 36. {HINT: Show that b36 = e; then show that for each factor k of 36, bk = e is impossible. [Example: If b12 = e, then b12 = (b3)4 = a4= e.] Derive your conclusion from these facts.}
# 2 Let a have order 6. If a has a fourth root in G, say a = b4, what is the order of b?
3 Let a have order 10. If a has a sixth root in G, say a = b6, what is the order of b?
4 Let a have order n, and suppose a has a sixth root in G, say a = bk. Explain why the order of b is a factor of nk.
Let
![]()
5 Prove that n and l are relatively prime. [HINT: Suppose n and l have a common factor q > 1. Then n = qn′ and l = ql′, so
![]()
Thus bn,k = e. (Why?) Draw your conclusion from these facts.]
Thus, if a has order n and a has a kth root b, then b has order nk/l, where n and l are relatively prime.
6 Let a have order n. Let k be an integer such that every prime factor of k is a factor of n. Prove: If a has a kth root b, then ord(b) = nk.